人工智能课程：计算思维培养的优质载体

张屹 刘金芳 贾杰

《义务教育信息科技课程标准（2022年版）》指出，要围绕数据、算法、网络、信息处理、信息安全、人工智能六条逻辑主线，设计义务教育全学段内容模块，组织课程内容，培养中小学生信息意识、计算思维、数字化学习与创新、信息社会责任四个方面的核心素养。“智能导航”是笔者自主开发的聚焦小学生计算思维培养的人工智能课程，课程内容依据计算思维的概念、实践和观念三个维度设计，教学方案采取将计算思维要素融入项目式学习活动的设计思路。

“智能导航”项目式学习共8个课时，教学对象是华中师范大学附属小学四年级两个自然班的学生。教学后，笔者借助国际Bebras测试题和自主编制的调查问卷，测评学生计算思维的发展水平。测评结果表明，学生的计算思维概念、计算思维实践和计算思维观念均有所提高。

一、前端分析

1.内容分析

“智能导航”课程选自张屹教授主编的《人工智能·计算思维》系列教材。该教材结合我国2021年颁布的《中小学人工智能课程开发标准（试行）》以及美国中小学人工智能教育指导工作组（AI4K12）发布的适用于中小学人工智能教育的概念等，从智能感知、表示与推理、机器学习、人机交互、社会影响五个方面规划与设计课程内容。其中，“智能导航”属于“表示与推理”概念下的内容。该课程巧妙地以规划观鸟路线活动，引领学生探究智能导航技术背后的算法原理，让学生通过自主设计一个模拟智能导航创意机器人，学习环境建模、贪心算法、枚举算法、选择算法等，以培养并发展学生的计算思维。

该课程包含四节内容：第一节“环境建模  抽象地图”引导学生通过建构湿地公园的模型图示，理解环境建模的要点，发展抽象思维；第二节“贪心算法  规划路线”引导学生通过在模型图示上计算最短观鸟路线，掌握贪心算法的原理与表示方法，学会以“一笔画”（从起点到终点不走重复路的路线）规划观鸟路线；第三节“枚举算法  路线优化”引导学生通过分析多条观鸟路线，学会规划路线的枚举算法，掌握最优路线的原理与计算方法；第四节“路线选择  智能导航”引导学生通过设计实现交互选择功能的模拟智能导航机器人，掌握选择算法的概念与设计方法，探索智能导航技术的奥秘，体会人工智能技术给生活带来的便利。

2.学习者分析

该课程内容实践性强，学习该课程内容前，学生需要掌握人工智能的基本概念，熟悉Mind+软件的基本操作。教师要在教学中关注学生掌握算法设计一般步骤的情况，以及操作Mind+软件时遇到的问题。

3.教学目标和重难点分析

基于以上分析，笔者将该课程的教学目标梳理如下：①知道环境建模的要点和步骤；②掌握贪心算法的概念，计算最短路线；③运用枚举算法比较各条路线的优缺点，掌握算法的适用情境；④掌握算法设计的一般步骤，编写实现交互选择功能的算法；⑤体会技术使路线规划更智能，培养对人工智能的兴趣。其中，教学重难点是环境建模的概念及运用，贪心算法、枚举算法、选择算法的概念與编写原则，设计“一笔画”路线，理解贪心算法得到的结果不一定是最合理的。

二、项目化设计与实施

项目式学习鼓励学生基于真实、完整的任务情境展开探究，通过自主探究与合作学习将抽象的知识与现实问题联系起来，通过解决问题掌握知识、原理与方法等。本研究采用项目式教学模式，创设了“设计实现交互选择功能的模拟智能导航机器人”的大任务，并将这个大任务分解成“地图大变身、规划最短观鸟路线、一笔画出观鸟路线、设计实现交互选择功能的算法”四个子任务。

任务一：地图大变身

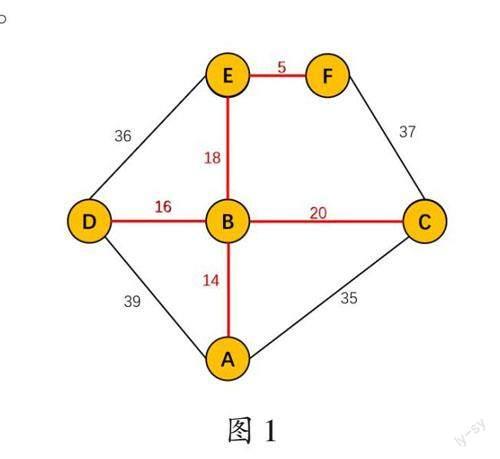
环境建模的目的是建立一个便于计算机规划路线的模型图示，这是智能导航机器人规划路线的重要前提。在本任务中，教师首先带领学生完成“地图大变身”游戏，让学生从复杂的湿地公园地图中提取关键信息，以观鸟景点为节点，以景点之间的道路信息为路线信息，根据任务单中的提示“一个景点用一个标注字母的圆圈表示，景点之间的一条路用一条线段表示，路的长度用数字标注在线段旁边”，将实际的地图抽象、简化，制作出观鸟地图的模型图示（如图1）。

这个建模过程很好地培养了学生的抽象能力，落实了计算思维实践维度目标。

任务二：规划最短观鸟路线

贪心算法能够帮助学生找到当下最短的观鸟路线。基于观鸟地图的模型图示，教师引导学生参与“贪心”侦察员游戏——侦察员从景点A出发，侦察到与景点A之间距离最短的景点B，找出A和B之间的最短路线，抵达景点B；再一次侦察，发现到景点B路线最短的是景点D，找出B和D之间的最短路线，抵达景点D。依此类推，教师逐步引导学生用贪心算法规划观鸟路线，明晰贪心算法的设计原则，以此培养学生的顺序概念，落实计算思维概念维度目标。

任务三：一笔画出观鸟路线

运用枚举算法解决问题时，计算机会对所有可能的情况进行检验、比较。在这个任务下，学生通过讨论分析，枚举出所有的观鸟路线。教师引导学生填写如表1所示的学习任务单，计算观鸟路线的总长，在模型图示中画出整个路线，并以小组为单位比较各条路线的优缺点。由此，学生理解了一笔画出的路线是最短的观鸟路程，发展了调试、迭代、批判思维，进一步落实了计算思维实践维度目标。

学生学会一笔画出观鸟路线后，将其命名为路线1；根据实际需要再选择另一条观鸟路线，将其命名为路线2。随后，教师先引导学生在Mind+软件上编写路线1和路线2的算法脚本，以此培养学生的分解思维；接着引导学生使用“选择模块”实现观鸟路线的选择功能，使机器人能够分别按照路线1或路线2行走，以此培养学生的条件与事件概念。这样教学，促进了学生实践维度和概念维度的计算思维目标的达成。

任务四：设计实现交互选择功能的算法

在前面的学习中，学生已经学会设计实现选择功能的机器人。为培养学生的迁移能力，教师教学时注重引导学生自主迁移已有的知识解决新情境下的问题，完成个性化路线设计的创意任务。在教师的引导下，学生先在任务单上编写参观图2中每个景点的路线脚本，然后设计实现交互选择功能的算法，并在Mind+软件上编写自己的创意算法，最后与同学分享自己的创意。在这个过程中，学生使用选择算法实现不同的计算机命令，不仅收获了算法知识，实现了自己的创意，还增强了对运用计算机算法解决实际问题的价值体验，有利于落实计算思维观念维度目标。

三、教学评价与结果分析

本研究根据“智能导航”案例改编Bebras测试题，从计算思维概念、计算思维实践、计算思维观念三个维度设计了前测问卷和后测问卷。

1.Bebras测试题分析

Bebras国际计算思维测试题主要用来测评计算思维概念维度与实践维度的水平。本研究根据“智能导航”课程主题，从已有的测试题中遴选合适的题目，测试小学生分解、抽象、算法、调试与一般化等计算思维发展水平。例题如下：

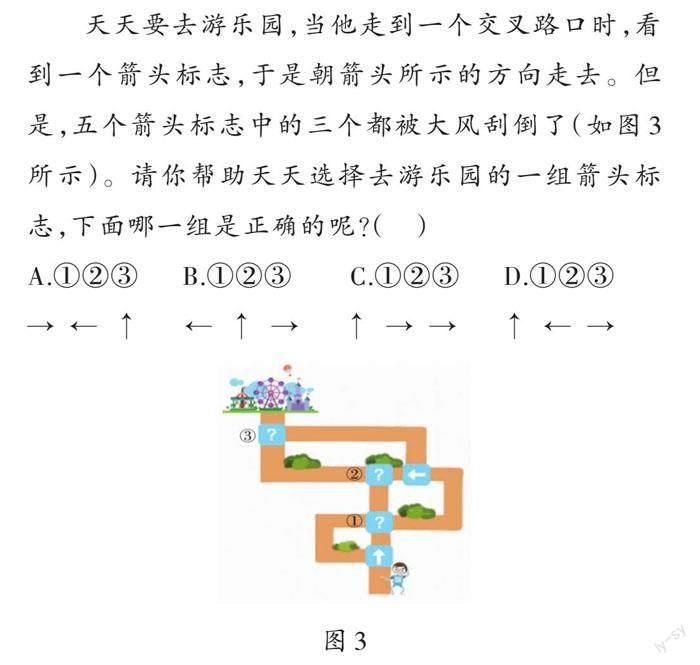
天天要去游乐园，当他走到一个交叉路口时，看到一个箭头标志，于是朝箭头所示的方向走去。但是，五个箭头标志中的三个都被大风刮倒了（如图3所示）。请你帮助天天选择去游乐园的一组箭头标志，下面哪一组是正确的呢？（  ）

A.①②③   B.①②③    C.①②③   D.①②③

→ ← ↑   ← ↑ →   ↑ → →   ↑ ← →

本测试题是学生学习环境建模知识后，测评学生计算思维概念水平的试题，考查学生能否将生活中的地图抽象成模型图示，以及对箭头的不同指向代表实际生活中不同路线行进方向的理解水平。其参考答案是A。

2.问卷测试题分析

本研究根据黄国祯和Brennan（布鲁南）设计的计算思维概念、计算思维实践与计算思维观念的成熟量表，结合实际教学经验，编制计算思维问卷前测试题和后测试题。测试题全部采用李克特五级量表。

在计算思维概念方面，问卷试题示例如下：①我知道观鸟路线是按照步骤规划的（顺序概念）；②我知道观鸟机器人可以走不同的路线（选择概念）等。在计算思维实践方面，问卷试题示例如下：①我能够将一个大的任务分解成多个小任务（分解思维）；②我能够将生活中的地图转变成由圆圈和线段组成的图示（抽象思維）；③我能够改正错误的算法（调试思维）等。在计算思维观念方面，问卷试题示例如下：①我能够将自己的想法表达出来（表达观念）；②我可以和同学合作完成学习任务单（合作观念）等。测评结果表明，学生学习人工智能课程后，在计算思维概念、计算思维实践和计算思维观念方面都发生了变化，三个维度上的后测均值均高于前测均值。

本研究通过制作前后测雷达图进一步分析学生对计算思维概念、计算思维实践、计算思维观念的各个要素的掌握程度（如图4所示，蓝色线条表示前测，橘色线条表示后测）。结果显示，学生在计算思维三个维度各个要素上的得分均值均有一定水平的提高。

中小学人工智能课程的开设与教学，既是信息科技课程标准提出的要求，也是教育发展的必然趋势。本研究遴选的“智能导航”课程主题贴近四年级学生的学情特点，课程内容设计以引导学生完成设计智能导航机器人的学习任务为明线，以培养学生了解和应用人工智能导航技术与原理为暗线，以项目式学习为教学模式，基于真实问题情境培养了小学生的计算思维。

（作者单位：华中师范大学人工智能教育学部）