Hermite 矩阵特征值分解的硬件加速

王卫江，李泽英，薛丞博，李翔南，任仕伟

（1.北京理工大学 集成电路与电子学院，北京 100081；2.北京理工大学 重庆微电子中心，重庆 401332；3.北京理工大学 信息与电子学院，北京 100081）

由于矩阵特征值分解的计算量大，其硬件实现一直是个难题[1]，但又因为在图像处理、阵列信号处理及机器学习领域被广泛应用，因而研究其硬件实现也具有一定的必要性[2].在阵列信号处理领域，经常性需要对复数矩阵进行求逆[3]和特征值分解[4]这样的运算，特别是对传感器阵列经过I/Q 采样得到的复信号的协方差矩阵进行特征值分解，且该矩阵为Hermite 矩阵[5].所以，设计出资源高效的针对Hermite 矩阵特征值分解的硬件加速模块具有重要的意义.

目前，用于在硬件层面上解决矩阵特征值分解问题的方法主要包括3 类：代数的方法[6]、Jacobi 算法[7]和QR 算法[8].代数的方法通过求解多项式方程来直接计算矩阵的特征值，其计算速度非常快，但是该方法不具备普适性，这是因为Abel-Ruffini 定理指出对于5 次及以上的多项式方程没有显式的代数公式.Jacobi 算法与QR 算法都使用迭代的方式进行求解，其中Jacobi 算法依赖于矩阵的平面旋转，QR 算法依赖于QR 分解[9]，可以通过不断的迭代将原矩阵变换为对角矩阵以完成特征值求解，此对角矩阵的对角线元素即特征值.两者相比，前者具有更高的计算精度，后者的收敛速度则更快[10].另外两者的应用场景也并不相同，经典的Jacobi 算法只能求解实对称矩阵的特征值与特征向量，改进后的复数域Jacobi 算法则可以进一步对Hermite 矩阵进行特征值分解，其运算复杂度约为O(n3)，QR 算法则可以对一般复矩阵进行特征值分解，但是其直接计算仅能得到矩阵特征值，如果想进一步得到矩阵特征向量，则复杂度将达到约O(n6)[2].

对于Hermite 矩阵特征值分解问题的硬件实现来说，当前主要有着两种不同的设计路线.文献[1,5-6, 11]先通过酉变换将Hermite 矩阵变为实对称矩阵后再使用了经典Jacobi 算法进行特征值求解，其中赵祎敏[1]使用了并行Jacobi 算法，完成对10×10 大小矩阵的特征值分解.文献[5, 11]则使用了串行双边Jacobi 算法进行特征值求解，其更具备普适性.文献[2, 12]直接使用复数域Jacobi 算法对Hermite 矩阵进行特征值分解.相比之下，酉变换时n×n大小的Hermite矩阵会变为2n×2n，这会导致在使用该方法对大矩阵进行特征值分解时延迟的增加，所以直接使用复数域Jacobi 算法是一个更好的选择.

本文针对Hermite 矩阵的特征值分解硬件实现问题，提出了一种兼容不同大小矩阵的复数域Jacobi 算法的硬件加速架构，并对其进行了仿真验证和FPGA 实现.本文首先介绍了复数域的Jacobi 算法，然后对其进行了量化分析，确定最佳小数位量化位宽，再使用流水线和逻辑复用技术进行了硬件加速设计，最后在Zynq-7000 系列FPGA 开发板上进行了性能分析与测试验证.试验结果表明，相比现有设计，本设计在相同条件下，具有更高的计算速度和更少的资源占用，具有更高的性价比.

1 复数域Jacobi 算法

Jacobi 算法是一种迭代求解的办法，经典的Jacobi 算法可以对实对称矩阵进行特征值分解，每次迭代需构造一个正交矩阵对原矩阵进行平面旋转，经过有限次的迭代之后可以将原矩阵的非对角线元素变得足够小，此时对角矩阵的对角线元素即特征值，每次构造的正交矩阵的累乘为特征向量.

复数域的Jacobi 算法[13]则可以对Hermite 矩阵进行特征值分解，区别主要在于每次迭代需要构造酉矩阵用于平面旋转.设输入Hermite 矩阵为H，那么其迭代过程主要包括4 步：

1) 寻找矩阵H的上三角矩阵中最大非对角线元素，并记录其行列信息i和j及其元素值；

2) 构造仅有4 个有效元素的酉矩阵U如式(1)

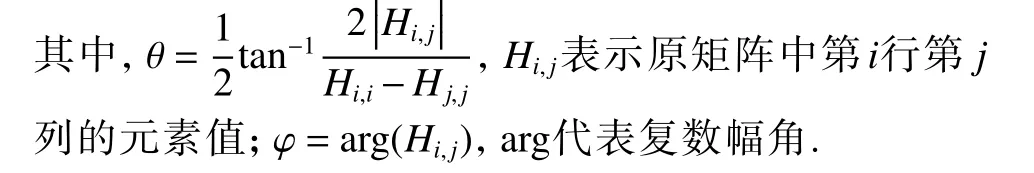
3) 通过矩阵乘对矩阵进行平面旋转，如式(2)所示.

此外，为了计算特征向量，还需使用式(3)计算酉矩阵的累乘

其中，V的初始状态为单位矩阵.

4) 判断迭代是否完成，有两种判断方式：1)迭代固定次数后完成；2)判断非对角线元素是否小于预设值，如果是则迭代完成.相对而言，前者的特征值分解所需时间固定，后者的计算精度则更有保证，本文为了保证足够的计算精度，采用了后者的方式.

2 量化位宽分析

在硬件实现中更利于实现定点运算，但定点运算会对最终计算结果的精度带来一定误差，为了在保证计算精度的同时不因为过大的量化位宽而带来不必要的资源消耗，所以在进行硬件加速设计之前确认量化位宽是很有必要的.

本文中使用均方根误差(RMSE)来表示计算精度，其计算公式为

式 中： sqrt 表 示 开 方 运 算；Dmi表 示MATLAB 计 算 得到的第i个特征值；Dhi表示硬件加速单元计算得到的第i个特征值；N表示特征值总数.

本设计的输入为16 bit 位宽的有符号数，小数位占10 位，以8×8 的Hermite 矩阵为例，研究构造出的酉矩阵的小数位量化位宽与均方根误差RMSE 之间的关系.以Matlab 中eig 函数的计算结果为参考，进行1 000 次蒙特卡罗试验，特征值的均方根误差RMSE与小数位量化位宽的关系如图1 所示.

图1 均方根误差与酉矩阵小数位量化位宽关系Fig.1 Relationship between RMSE and fractional quantization bit width of unitary matrix

从图1 中可以看到随着小数位量化位宽的增加，特征值均方根误差不断缩小，在10～15 范围内快速缩小，在15～30 范围内基本保持不变，此外，考虑到量化位宽的增加必然会导致额外的硬件资源开销.所以，对于8×8 大小的Hermite 矩阵来说，采用15 位宽小数点量化是最优选择.

3 硬件加速架构

复数域Jacobi 算法的硬件加速架构如图2 所示，本设计以8×8 大小的Hermite 矩阵为例进行设计，但相同的电路架构同样可以应用于其他大小的Hermite矩阵.电路内部主要包括一个用于存储特征值与特征向量的存储单元和3 个计算单元，分别是寻找最大非对角线元素、构造酉矩阵以及更新特征值矩阵和特征向量矩阵.判断迭代是否完成则利用了寻找最大非对角线元素单元，其仅需在寻找到最大非对角线元素之后判断该值是否小于设定阈值即可，通过这种方式的逻辑复用进一步降低硬件资源的消耗，具体的阈值设置需要根据实际情况确定.

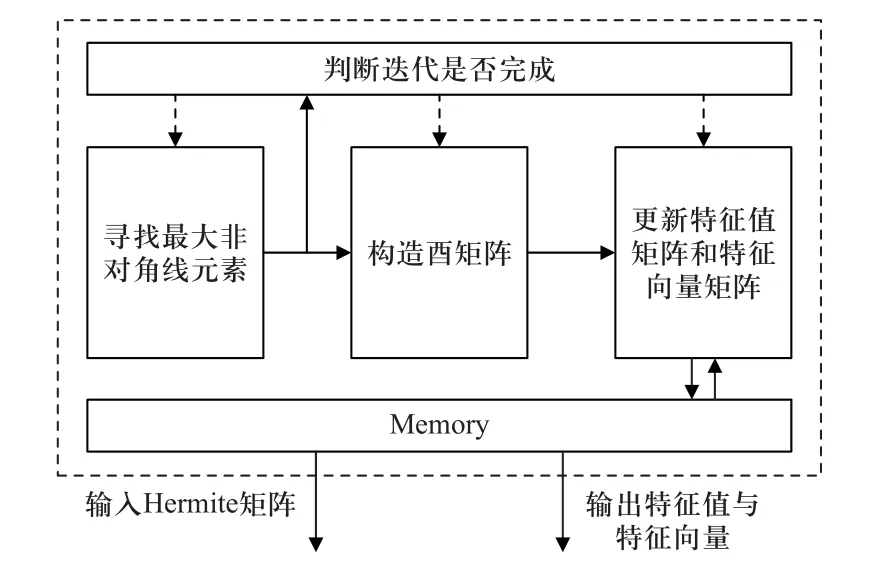
图2 Hermite 矩阵特征值分解的硬件加速架构（虚线表示控制信号，实线表示数据传递）Fig.2 Hardware acceleration architecture of Hermite matrix eigenvalue decomposition (dotted line indicates control signal, solid line indicates data transmission)

3.1 寻找最大的非对角线元素

由于输入矩阵为Hermite 矩阵，其具有共轭对称性质，所以寻找最大的非对角线元素只需要遍历上三角矩阵中的非对角线元素，共27 个元素即可.考虑到Hermite 矩阵的所有元素均为复数，如果比较模长则还需进行乘法和开根号运算，这将增加大量的计算和延时.

实际上，只需对比元素实部值的大小同样可以达到迭代逼近对角矩阵的目的，这种方式的寻找最大的非对角线元素的电路结构如图3 所示.

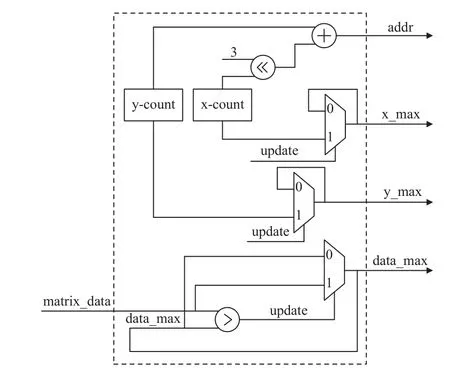
图3 寻找最大的非对角线元素架构Fig.3 Architecture for finding largest off-diagonal elements

首先分别使用行列计数器x-count 和y-count 来表示需要进行对比的元素的位置信息，Hermite 矩阵的所有元素均按照从左上角到右下角的顺序存储在RAM 中，所以可以用式(5)计算得到地址信号用于将所需要的元素值从RAM 中读出

此处8 为2 的整次幂，所以可以通过左移3 位来代替乘法运算.

为了找出最大的非对角线元素的值及其行列信息，还需要使用3 个寄存器x_max、y_max 和data_max，在开始之前将data_max 初始化为0，判断如果当前输入的值大于记录的最大值data_max 那么就将当前元素的值更新到data_max 并将行列信息值xcount 和y-count 更新到寄存器x_max 和y_max 中去，该方案共需要1 个比较器和3 个两路选择器.在比较完所有元素后将3 个寄存器的值输出即可得到最大的非对角线元素值及其行列信息.

3.2 构造酉矩阵

需要构造的酉矩阵如式(1)所示，其拥有4 个有效元素，需先后计算 cosθ 、 sinθ 、 eiφ和 e-iφ再进行数据相乘得到.

由欧拉公式

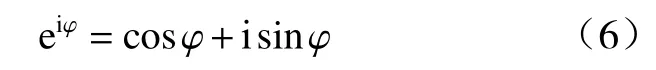
可知， eiφ和 e-iφ实部相等，虚部为相反数，又因为φ=arg(Hi,j) ，所以

经过上述分析可知，计算中涉及到的复杂运算包括开方运算、反三角函数 tan-1、三角函数sin 与cos 函数以及除法运算，前三者均可使用CORDIC 核IP 实现，除法运算则可使用现有除法器IP 实现，总的构造酉矩阵的电路结构如图4 所示.

图4 构造酉矩阵的电路结构（虚线包括的cos 和sin 表示两者共用一个CORDIC 核即可同时完成计算）Fig.4 The circuit structure for constructing a unitary matrix (the cos and sin included in the dotted line indicate that the two share a CORDIC core to complete the calculation at the same time)

从图4 中可以看到，构造酉矩阵的电路结构共需要3 种不同类型的基于CORDIC 核的运算，而且它们的功能并不相同，所以需要例化3 次.此外，运算中涉及到3 次除法，其功能都是一样的且输入值并不相互依赖，所以可以通过使用流水线结构的除法器，在相邻的计算周期完成3 次除法运算，共用一个除法器IP 以减少逻辑资源的消耗.所以只需符号变换即可同时得到两者数据，这点在图4中未画出.

3.3 更新特征值矩阵与特征向量矩阵

在完成酉矩阵U的构造之后还需使用式(2)和式(3)进行特征值矩阵和特征向量矩阵的更新，因为两者之间不存在依赖关系，因而可以并行计算，如图5所示.

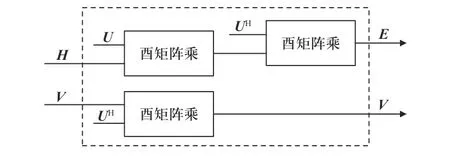
图5 更新特征值矩阵与特征向量矩阵电路Fig.5 Circuit for updating eigenvalue matrix and eigenvector matrix

由于3.2 节中构造的酉矩阵仅有4 个有效元素，所以在进行酉矩阵左乘时只会改变原矩阵的两行元素，进行酉矩阵右乘时只会改变原矩阵的两列元素[12].所以，利用这一特性可以避免大量的无效运算，进一步提高运算速度，酉矩阵左乘的电路结构如图6 所示.

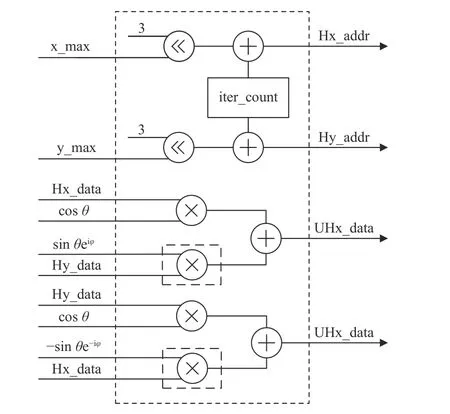
图6 酉矩阵左乘（带虚线框的乘法表示复数乘）Fig.6 Unitary matrix left multiplication (multiplication with dashed box indicates complex multiplication)

以酉矩阵U左乘原始矩阵H为例，酉矩阵乘单元包括用于读取原始矩阵对应元素的地址生成单元以及用于完成矩阵乘的计算单元.地址生成单元根据3.1 节寻找最大非对角线元素单元输出的行列信息

对于最终的结果输出，eiφ和 e-iφ虚部为相反数，生成Hx_addr 和Hy_addr，将所需要的H矩阵的元素读出.由于酉矩阵的特性，酉矩阵乘的计算单元完成一个元素的求解仅需两对数据相乘后再相加，这里使用了两路并行计算单元来同时计算有变化的两行数据，所以对于8×8 大小的矩阵来说，仅需iter_count迭代8 次即可输出所有的酉矩阵乘的结果，这里省略了输出数据的地址信号.

图6 中的虚线框中的乘法表示复数乘法，可以使用式(7)计算，利用乘法器和加法器即可完成.

4 性能分析

本文提出的硬件加速设计对8×8 大小的Hermite矩阵进行特征值分解的仿真时序图如图7 所示，其是在Modelsim 软件上的仿真结果.可以看出硬件加速同样需要进行多次迭代才能完成矩阵的特征值分解，其中“JACOBL_CNT”为迭代次数计数器.对于本次测试的特定矩阵来说，需进行26 次迭代.

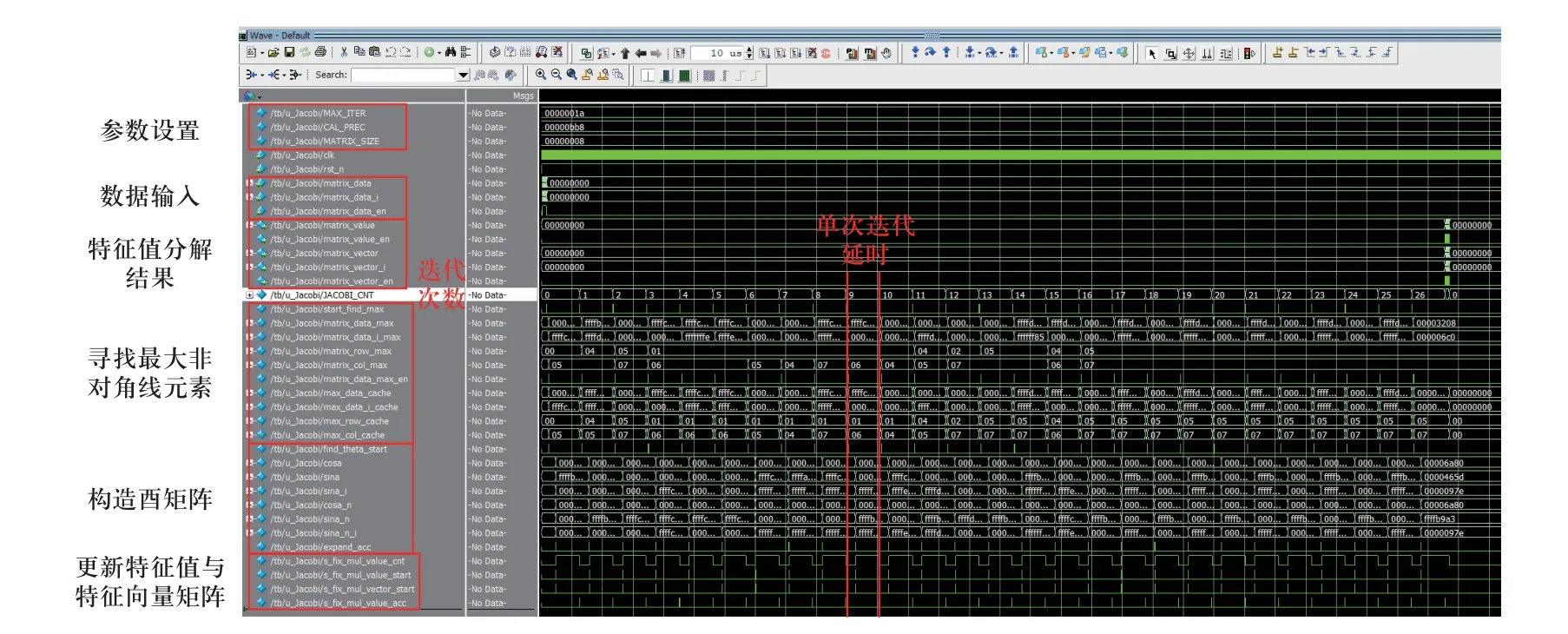
图7 8×8 大小的Hermite 矩阵特征值分解的仿真时序图Fig.7 Simulation sequence diagram of eigenvalue decomposition for 8×8 Hermite matrix

衡量硬件加速设计性能优劣的3 个指标分别是计算精度、计算速度以及资源占用情况，下边将分别对其进行探讨分析，并与现有的硬件解决方案进行对比.

4.1 计算精度分析

通过第2 节的分析，最后确定了采用小数位15位位宽的定点运算性价比最高，对计算精度的仿真结果表明其特征值的均方根误差RMSE 为0.097 0.

具体的，对于随机生成的一个8×8 大小的Hermite矩阵，其硬件计算结果与Matlab 中eig 函数计算结果相比误差如表1 所示.

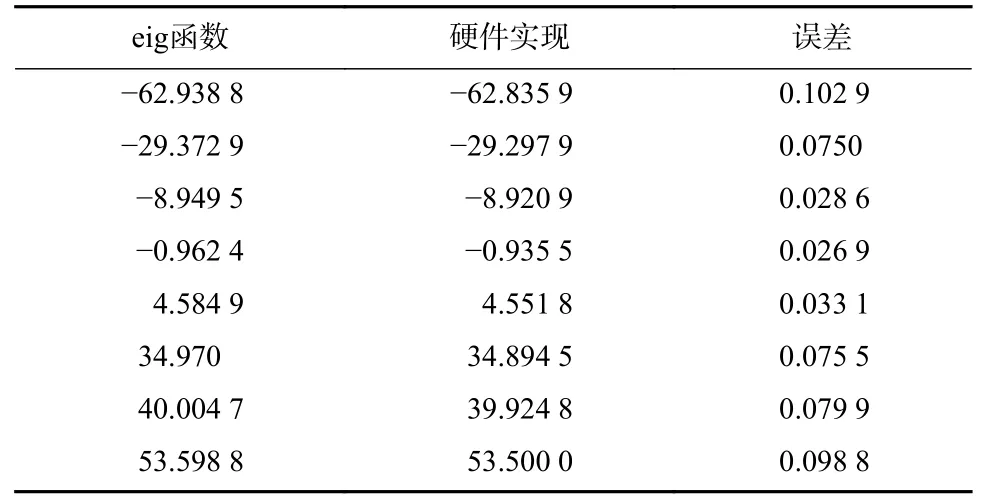
表1 硬件实现误差分析Tab.1 Error analysis of hardware implementation

可以看出，与eig 函数相比，本设计的计算精度较高，基本可保证在0.1 以内，可满足实际工程需求.

4.2 计算速度分析

硬件实现的计算速度由计算所需周期数和时钟频率共同决定，Jacobi 算法是一种迭代求解算法，其延时与单次迭代所需时间有很大关系.所以，下边将先对本设计中的单次迭代所需延时进行理论分析，然后将实际延时与现有硬件设计方案进行对比.

本设计的总体结构如图2 所示，其单次迭代的延时主要取决于寻找最大非对角线元素、构造酉矩阵以及特征值矩阵与特征向量矩阵的更新.寻找最大非对角线元素的电路结构如图3 所示，地址生成单元与比较单元并行计算，共需比较27 个元素因而需要27 个时钟周期；酉矩阵生成单元的关键路径为计算 sinθeiφ，其电路如图4 所示，中间过程数据位宽为32 bits，则除法器运算需要32 cycle，CORDIC 核运算需要35 个cycle，其他乘法和移位运算均在一个cycle 内完成，那么总的酉矩阵计算单元共需要142个时钟周期；最后的特征值矩阵和特征向量矩阵更新单元中，特征值矩阵和特征向量矩阵可以并行计算，且特征值矩阵需进行两次矩阵乘法，其为关键路径.酉矩阵乘法的电路结构如图6，采用流水线的复数乘法器，其延迟为13 个时钟周期，所以进行一次酉矩阵乘法需要20 个时钟周期，更新特征值矩阵需要40 个时钟周期.总的来说，完成一次迭代共需要209 个时钟周期.

本设计使用Zynq-7000 系列开发板进行开发，综合设计的最大频率可达到175 MHz，其实际计算速度与其他设计方案的对比如表2 所示.

表2 计算速度对比Tab.2 Computational speed comparison

与现有的设计相比，本文提出的设计在计算速度上更占优势，其中赵文扬[2]中的设计与本文一样使用了复数域的Jacobi 算法直接对Hermite 矩阵进行特征值分解，但本文所构造的酉矩阵简单且使用了流水线的设计方法.YAN 等[14]则使用了酉变换将Hermite 矩阵变为实对称矩阵再进行特征值分解，其引入和更多的计算步骤.GUPTA 等[7]则耗时最长，尽管其使用了并行Jacobi 的方法，但是一方面它使用了酉变换，所以需要对16×16 大小的实对称矩阵求解，另一方面其设置的精度更高，所以需要迭代更多的次数，所以耗时大大增加.

4.3 所需资源分析

本文所提出的硬件设计使用Verilog 语言描述，同时还使用了现有的硬件IP，主要包括由CORDIC 核构成的反三角函数 tan-1运算、三角函数sin 和cos 以及流水线结构的除法器.三者所需逻辑资源LUTs 分别是3 454、3 559 和1 728.除此之外，还需进行复数的乘加运算及逻辑控制，所需硬件资源将增加.

具体的，本设计在Zynq-7000 系列FPGA 上进行逻辑综合后，与其他设计方案在硬件资源消耗情况的对比如表3 所示.

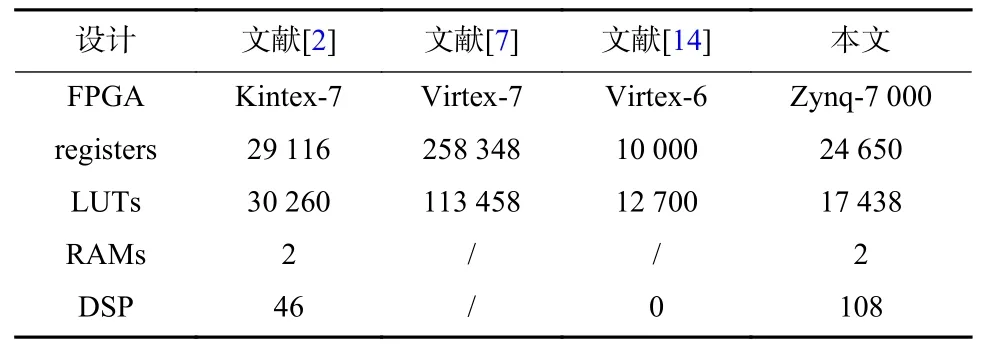
表3 硬件资源情况对比（/表示论文中未给出）Tab.3 Comparison of hardware resources (/ means not given in the paper)

可以看出，本文与文献[2]均使用了复数域的Jacobi 算法直接对Hermite 矩阵进行特征值分解，在该情况下本设计所需资源更少，这主要是本设计采用了更加简单的酉矩阵构造方法.与实数域的Jacobi 算法的文献[14]相比，实数域的Jacobi 算法的硬件设计所需资源要少很多，这是因为实数域的Jacobi 算法不需要进行复数的乘除运算且只需要更少的三角函数计算.文献[7]则采用了并行Jacobi 算法，其并行度更高，且采用了20 位的小数位量化位宽，这些都使得其所需资源的增加.总的来看，本文的设计对于Hermite 矩阵的求解在相同条件下具有更优的性能.

5 结 论

本文针对Hermite 矩阵的特征值分解问题，提出了一种基于复数域Jacobi 算法的资源高效的硬件加速方案，且该方案可应用于不同大小的Hermite 矩阵.本文首先从算法层面介绍了更为简单的复数域Jacobi 算法的计算流程，其构造了更便于硬件实现的酉矩阵.然后重点介绍了硬件加速方案的架构设计，特别是将判断迭代是否完成与寻找最大非对角线元素相结合，减少了单次迭代的延迟.在设计寻找最大非对角线元素、构造酉矩阵和更新特征值矩阵和特征向量矩阵的过程中使用了较多的逻辑复用和流水线技术，尽可能地减少不必要的资源占用并提高计算速度.

最后，将本设计在Zynq-7000 系列FPGA 开发板上进行了硬件实现，经过试验验证发现本设计在仅占用17 438 LUTs 和24 650 Registers 资源情况下在34.42 μs 内即可完成对8×8 大小的Hermite 矩阵的特征值分解，相比于现有的设计来说其资源更加高效.