开展多维探究发展核心素养——圆维曲线一类三点共线问题的探究及思考

广东省深圳市高级中学理慧高中(518040) 高军

1 引言

《普通高中数学课程标准(2017 年版)》必修课程主题五和选择性必修课程主题四设计了“数学建模和数学探究活动”主题,指出自主探索和合作交流是学生学习数学的重要方式,要让学生获得进行数学探究的切身体验和能力[1]. 笔者认为,深化普通高中课程改革的核心之一是转变教师的教育理念,坚持教学方式的改革,倡导积极主动、敢于质疑、自主探究、合作交流的学习方式. 因此,开展多维探究,构建有效探究式教学课堂是促进学生有效学习、发展数学核心素养的必然要求. 以下教学案例是基于这种理念下的尝试,与同行交流.

2 案例呈现

2.1 问题

如图1, 已知椭圆G:直线l:x= 4与x轴相交于点E,过椭圆G右焦点F的直线与椭圆相交于A,B两点, 点C在直线l上且BC//x轴,点M为线段EF中点,求证: 点A,M,C三点共线.

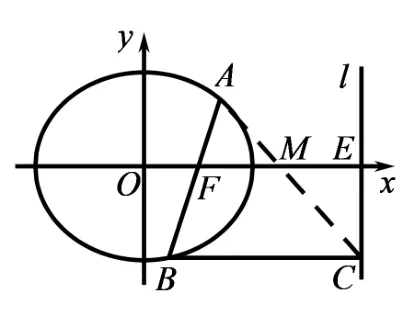
图1

2.2 解法探究

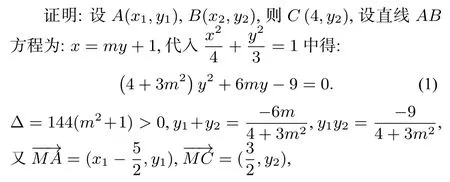
思路一(转化为向量共线)或定值问题,拓展了学生思维.

思路五(转化为几何证明)

评注: 结合几何性质及椭圆第二定义解决问题. 圆锥曲线第二定义在教材的阅读材料有专门介绍. 这说明好的方法源于丰富的知识储备,知识就是力量.

小结: 思路一和思路五是直接法,从代数和几何角度直接求证. 解法二、三、四是间接法,将求证结论合理进行转化,分别通过线线平行、定点问题、定值问题的解决来求证,蕴含同一法原理,体现了转化与化归的数学思想.

2.3 变式探究

一个问题的研究往往孕育着新的问题的产生,对应思路二、三、四,转化题目的条件和结论,可以得到有关线线平行、定点问题、定值问题为结论的三个命题. 还有没有其它变式,是与椭圆焦点弦有关且以三点共线为结论的命题? 经过教师引导,学生的独立探究、小组合作得到如下变式:

变式1如图2,已知椭圆直线l:x=4与x轴相交于点E,过椭圆G右焦点F的直线与椭圆相交于A,B两点,点A关于x轴的对称点为A1,求证: 点A1,B,E三点共线.

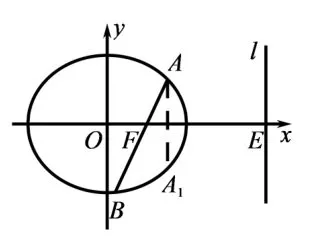
图2

变式2如图3,已知椭圆设椭圆的左、右顶点分别为M,N,A是椭圆上异于M,N的任意一点,点F为椭圆的右焦点,直线AF交椭圆于另一点B,直线AN交直线l:x=4 于点Q,求证: 点M,B,Q三点共线.

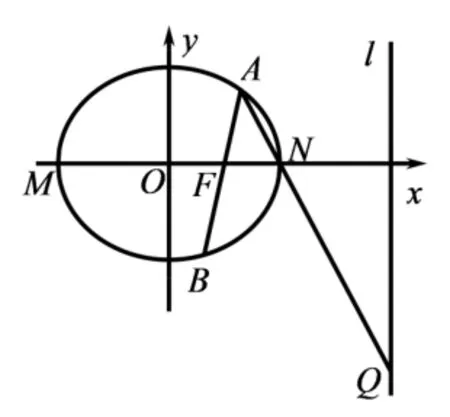
图3

变式3如图4,已知椭圆椭圆的左、右顶点分别为M,N,过椭圆G右焦点F的直线与椭圆相交于A,B两点,直线MA与直线l:x= 4 相交于点E,过点F作直线FD⊥FE与直线l:x= 4 相交于点D,求证: 点M,B,D三点共线.

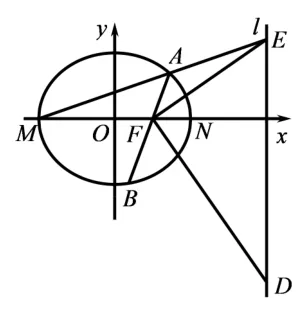
图4

变式4如图5, 已知椭圆过直线l:x= 4 上任意一点E作椭圆两条切线,切点分别为A,B,点F为椭圆的右焦点,求证: 点A,F,B三点共线.

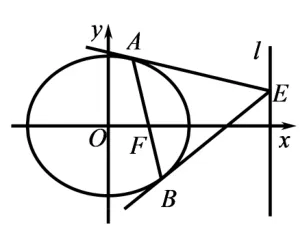
图5

评注: 这些命题都是对椭圆中一类有关焦点弦的命题,经过条件和结论的适当转换进行变式而成,类比前面三点共线问题的解决思路,这四个命题容易得到证明.

数学教育家波利亚说过:“解完题后还能不能换个角度考虑一下? 还能不能再推广呢? ”将椭圆类比到双曲线或抛物线,是否也有类似的结论?

2.4 类比探究

鼓励学生大胆猜想,引导学生结合图形进行验证,将椭圆类比到双曲线得到以下结论:

结论一已知双曲线直线与x轴相交于点E,过双曲线G右焦点F的直线与双曲线的右支相交于A,B两点,点C在直线l上且BC//x轴,点M为线段EF中点,则点A,M,C三点共线.

结论二已知双曲线直线与x轴相交于点E,过双曲线G右焦点F的直线与双曲线相交于A,B两点,点A关于x轴的对称点为A′,则点A′,B,E三点共线.

结论三已知双曲线设双曲线的左、右顶点分别为M,N,点F为双曲线的右焦点,A是双曲线上异于M,N的任意一点,直线AF交双曲线于另一点B,直线AN交直线于点Q,则点M,B,Q三点共线.

结论四已知双曲线设双曲线的左、右顶点分别为M,N,过双曲线G右焦点F的直线与双曲线右支相交于A,B两点, 直线MA与直线相交于点E,过点F作直线FD⊥FE与直线l相交于点D,则点M,B,D三点共线.

结论五已知双曲线过直线上一点E作双曲线两条切线,切点分别为A,B,点F为双曲线的右焦点,则点A,F,B三点共线.

评注: 如果将椭圆类比到抛物线,也会有相关类似的结论. 我们发现,问题及变式的条件有共同点: 直线AB过圆锥曲线焦点,直线l为圆锥曲线的准线. 如果直线AB过x轴上任意一点,是否也有更一般的结论?

2.5 归纳探究

条件是非本质的特殊情况,由特殊到一般,作如下推广:

结论六如图6,已知椭圆直线与x轴相交于点E,过x轴上的点T(t,0)的直线与椭圆相交于A,B两点,点C在直线l上且BC//y轴,点M为线段ER中点,点A,M,C三点共线.

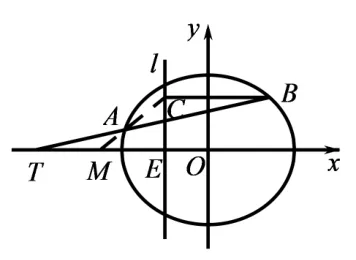
图6

如果直线AB过x轴上一点,也可作如下推广:

结论七如图7,已知椭圆直线与y轴相交于点E,过y轴上的点R(0,r)的直线与椭圆相交于A,B两点,点C在直线l上且BC//y轴,点M为线段ER中点,点A,M,C三点共线.

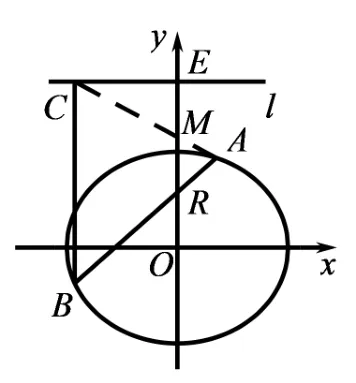
图7

评注: 由合情推理,前面结论可进行一般情况的推广,可以得到很多的新的命题和结论. 以上结论的推证过程与案例的探究过程相仿,这里从略.

3 教学思考

3.1 渗透数学思想,多解探究,发展核心素养

《普通高中数学课程标准(2017)》指出:“……突出数学主线,凸显数学的内在逻辑和思想方法. ”在案例的探究过程中,渗透转化与化归、数形结合、函数与方程等数学思想,体现了数学思想在解题中的重要作用. 通过数学思想的融会贯通,引导学生从多角度思考问题,有利于提高学生分析问题解决问题的能力,发展学生逻辑推理、直观想象、数学运算等数学核心素养.

3.2 以问题为导向,变式探究,发展核心素养

顾明远先生指出:“课堂教学是培养学生思维的主渠道,只有会思考并提出问题,才能培养学生的批判性思维、创新思维的能力. ”变式探究中的四个变式都是学生根据以往的数学学习经验及一类焦点弦的解题模型,对原命题的条件和结论进行变式提出的,体现了创新意识和创造性. 可见构建以问题为导向的探究式课堂,可以唤起学生对数学学习的热情,有利于发展学生的数学抽象、数学建模、逻辑推理等数学核心素养.

3.3 探寻数学本真,合情探究,发展核心素养

在类比归纳探究中,学生将椭圆类比到其它的圆锥曲线,将直线AB过焦点推广到直线AB过坐标轴上任意点,得到了一系列的相关结论. 一方面有效地将前后所学知识融合在一起,帮助学生建构完整的知识体系;另一方面可以提高学生的思维灵活性,激发学生的创造思维. 教师要有意识地去挖掘与合情推理有关联的数学问题,让学生养成运用合情推理去解决问题的习惯,发展学生逻辑推理核心素养.