防空反导战术级指挥控制目标分配发展研究

刘祥雨 王刚 李腾达 夏智权

摘要：      目标分配是指挥控制决策阶段的核心。 许多学者对目标分配问题进行了大量研究， 在目标分配模型和算法方面取得了较大进展， 但随着马赛克战、 分布式作战、 网络中心战等新型作战样式的演变和发展， 现代防空作战复杂度空前提升。 针对防空反导战术级指挥控制目标分配暴露出不同作战场景适应能力弱、 博弈对抗性和鲁棒性不足等问题， 通过总结梳理目标分配研究现状， 从攻防体系的发展角度深入探讨了目标分配理论研究在防空反导实际应用过程中所面临的挑战， 剖析了目前防空反导战术级指挥控制目标分配存在诸多问题的根本原因， 并针对不足提出了防空反导目标分配智能化、 网络化、 实战化的发展需求。

关键词：     目标分配； 防空反导； 人机交互； 杀伤网； 战术级; 指挥控制系统

中图分类号：      TJ760    文章编号：     1673-5048（2023）04-0067-11

文献标识码：    A    DOI： 10.12132/ISSN.1673-5048.2022.0273

0引言

随着现代战争的飞速发展， 战争方式快速更迭。 进入信息时代， 信息高度集中、 数据量激增的作战体系已成为主要的作战系统。 面对复杂多变的战场环境， 仅仅依靠指挥者的指挥能力难以驾驭现代战争， 必须要通过计算机技术、 自动化控制技术、 通信技术、 感知技术等对战场态势进行信息收集和融合， 指挥控制系统根据融合后的信息进行辅助决策， 从而对战场态势做出快速、 合理的判断， 为指挥员做出决策提供可行依据［1］。

战术级防空反导指挥控制决策阶段研究的主要问题是目标分配问题。 在新型作战样式的挑战下， 防空反导战术指挥控制目标分配也不断发展， 但是诸多模型和算法难以应用实际作战。 针对此问题， 本文以防空反导战术级指挥控制目标分配为切入点， 分析目标分配模型及算法在实际作战过程中存在的问题， 在此基础上提出目标分配的发展需求， 为目标分配研究发展提供方向。

1基本內容

1.1目标分配概念及分类

目标分配（Target Assignment）， 也叫武器-目标分配（Weapon-Target Assignment， WTA）， 是指挥控制系统根据目标运动参数、 数量和地空导弹火力单元数量、 性能、 弹药资源等， 将目标分配给不同火力单元拦截， 自动完成目标和火力单元的最优配对关系并实现作战效能最大化的过程［2］。

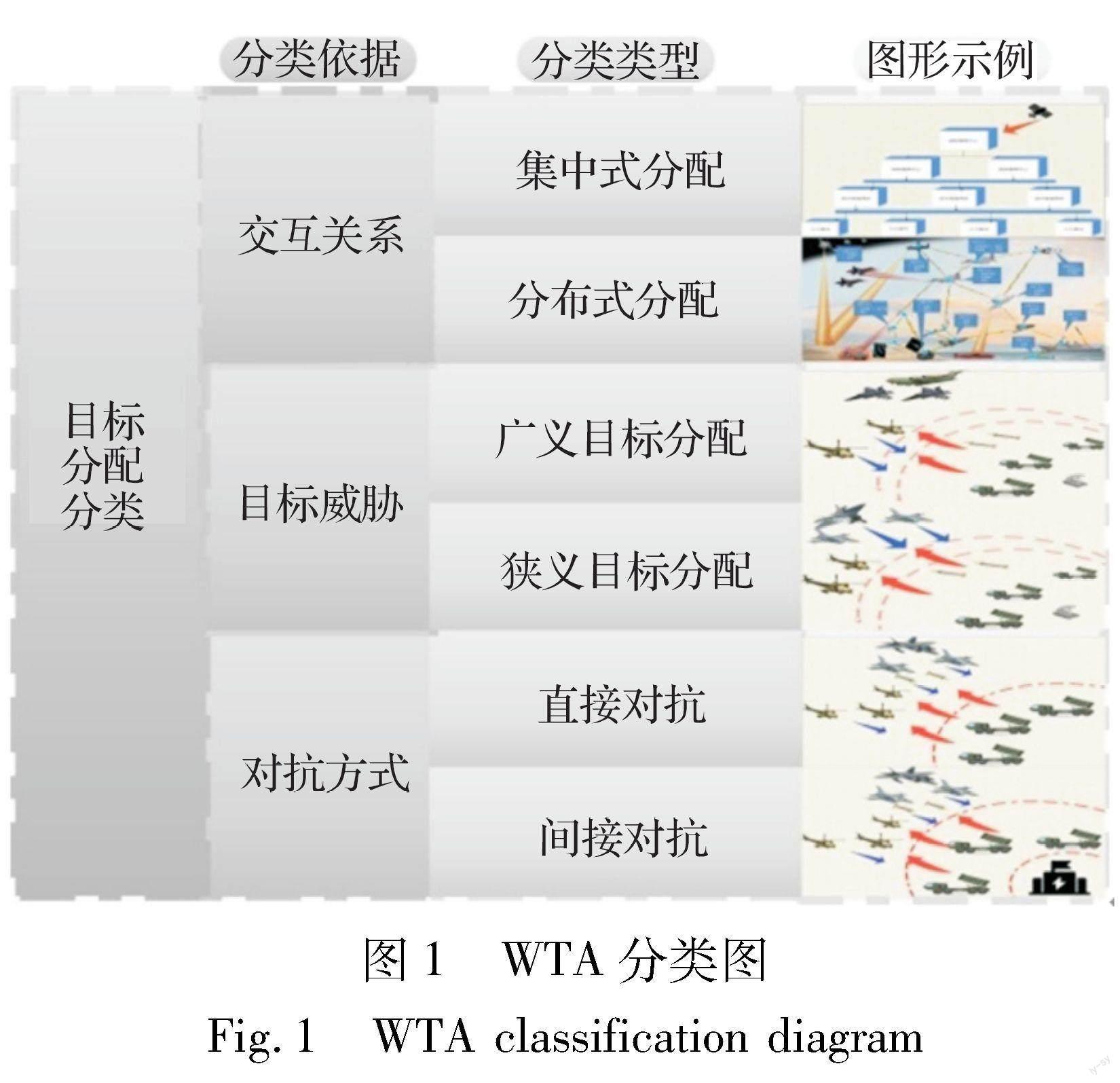
目标分配的分类如图1所示。 从系统的指挥方式分析， 目标分配分为集中式分配和分布式分配， 集中式分配是一种上级指令式的分配方式， 便于统一协调武器资源， 发挥武器系统的整体威力；  分布式分配是同等级的分配方式， 交互关系是双向的。 从判定目标是否具有威胁的角度， 可以分为广义的目标分配和狭义的目标分配。 广义的目标分配指目标既包含有攻击力和不确定是否有攻击力的目标， 狭义的目标分配是只包含攻击能力的目标。 从作战双方的对抗方式， 可以分为直接对抗式和间接对抗式， 两种类型的主要区别是来袭方攻击对象不同［3］。

1.2WTA建立的基本模型与算法研究

WTA问题的研究主要集中在目标分配模型和算法研究两方面， 常见的建模方法主要有两类：

（1） 基于复杂适应系统理论的建模方法。 该方法具备自适应性主体， 能够与环境进行交互学习， 在复杂系统中具备适应性主体和解决非线性问题等特征， 采用的技术包括Agent建模方法（Agent-Based Modeling， ABM）及通用的可视化建模语言等。

（2） 基于严格数学理论的建模方法。 通过具备一致性、 独立性和完备性的数学公理系统， 抽象化和逻辑推理地对数学模型进行分析描述， 以解决现实问题， 如整数规划、 马尔可夫决策过程、 图论、 Petri网等， 这些理论方法可以从数学的角度定量分析模型的可行性、 合理性、 有效性［4］。

模型的研究主要包括模型假设、 目标函数的选择、 约束条件和时间因素［5］， 其中动态模型与静态模型的主要标志指是否考虑时间因素。 以简单的静态目标分配模型为例， 其模型如图2所示。 防御方和来袭目标的武器状态固定， 所有参数公开且不会变化， 防御武器与对应拦截目标的杀伤概率已知， 防御方的作战目的是分配拦截武器去拦截目标， 使来袭目标的总威胁度最小。

在静态的目标分配中， 有两个假设：

（1） 同时对火力平台分配目标， 且防御武器发射拦截弹后可获得目标状态。

（2） 武器-目标分配关系之间相互独立。

在一场防空作战中， 袭击方派出n个来袭目标B1， B2， …， Bn， 防御方有m个火力平台A1， A2， …， Am。 第i（i=1， 2， …， m）个火力平台最多可使用Ti个武器， 对目标Bj（ j=1， 2， …， n）最多可以使用Cj个武器， 第j个威胁目标的威胁度为Vj， 第i个火力平台Ai成功击毁目标Bj的概率为qij， 武器最佳分配以使最终的来袭目标总体威胁度最小为目标。

若分配武器平台Ai迎击目标Bj， 目标选择的决策变量xij=1， 否则xij=0。 优化目标函数：

（4）同一火力平台不能同时攻击两个或两个以上目标， 即

xij=0或1（5）

以上为简单的WTA数学模型构建过程， 即便构建静态模型， 也要考虑众多约束条件， 如果构建基础的动态目标分配数学模型， 则要考虑更多的动态因素， 因此， 目标分配的理论求解与实际应用都是极为复杂的， 需要不断发展研究。

关于目标分配算法上的研究总体上可以分为两类： 集中式求解和分布式求解。

（1） 集中式求解方法

集中式求解方法主要集中在两个方向： ①多阶段匹配优化算法， 如动态规划、 整数规划等； ②智能算法， 如遗传算法、 免疫算法、 粒子群算法等。

（2） 分布式求解方法

分布式求解方法主要集中在两个方向： ①基于市场机制的求解算法， 如拍卖算法、 合同网等； ②群智能算法， 如人工鱼群算法、 蚁群算法等［4］。

1.3WTA模型与算法的国内外发展状况

1.3.1WTA模型发展情况

在20世纪， 导弹技术不断发展， 使得进攻方可以利用导弹从远距离攻击防守方的保护资源。 为了消除这种空袭威胁， 防空概念应运而生， 防空武器装备性能也不断提高， 从最初的单通道武器系统逐渐演变为多通道武器系统， 可分配的导弹资源数量也随之提高， 对有效分配防空资源使得资源利用最大化的研究也随之出现和发展。 WTA早期的研究主要集中在导弹防空等特定领域， 随后不断丰富发展。

（1）  整数规划模型

整数规划是指规划中的变量限制为整数， 常见的有纯整数规划、 混合整数规划、 0-1规划等。 其模型多样， 数学逻辑严谨， 有很大的应用领域。 WTA问题最初建立的数学模型为非线性整数规划模型， 开始于Manne的开创性工作， 在随后的几年里， 改进模型得到发展， 包括假设条件较少的模型和以时间为参数的模型。 Kline等通过传统的数学规划模型对武器目标分配问题进行求解［6］； 和传统的非线性模型不同， 陆一平等在不丧失模型最优解的前提下， 通过限定对目标分配武器的数量降低线性整数规划（ILP）模型维数， 将WTA问题建模为线性整数规划模型［7］； Li等通过验证传感器和武器的协同作战能力取决于SWTA方案， 在SWTA问题综合框架的基础上， 建立传感器和武器协同交战模式的整数规划模型［8］。

（2）  基于马尔可夫决策模型

为解决静态目标分配模型的适用性差等问题， 动态目标分配（Dynamic Target Assignment Weapon， DWTA）模型被广泛研究。 韩松臣等较早对此模型進行研究， 将马尔可夫决策过程应用于目标分配决策中， 考虑作战的多阶段特点， 追求决策的长期效益［9］； 张庆波等分析防空系统的作战特点， 将马尔可夫决策过程应用于防空系统目标分配中［10］； 蔡怀平等运用随机过程理论证明了动态WTA过程的马尔可夫性， 并且给出了决策过程的状态转移概率的解析表达式， 对于在目标分配问题中应用马尔可夫决策过程提供了理论依据［11］。

（3）  图论

作为运筹学的一个分支， 图论是一种研究节点和边组成的图形的数学理论和方法， 在目标分配问题中， 与其紧密联系的是匈牙利算法。 柳毅等运用此方法从单目标分配推广至多目标分配， 并验证此方法的有效性［12］； 黄力伟等利用匈牙利算法求解目标分配问题， 方法简单， 具有应用价值［13］； 殷红运用模糊匈牙利算法在决策过程中将主客观因素有机地结合起来， 有效解决炮兵火力单元的分配最优化问题［14］； 周洪喜等利用改进的匈牙利算法求解多导弹阵地协同拦截多目标模型， 有较快的求解速度［15］； 张进等提出统一效率矩阵， 在匈牙利算法耗时短、 求解稳定的基础上提高了算法的优越性， 进一步丰富了此方法在武器-目标分配问题中的运用［16］； 常雪凝等将匈牙利算法和模拟退火进行混合， 在求解多阶段武器目标分配问题方面较变邻域搜索算法减少了计算时间［17］。

（4） Agent建模方法

随着人工智能技术在军事领域中的应用， 对Agent建模方法的研究逐渐深入。 利用Agent技术的智能性和代理能力， 可以将目标分配这样庞大复杂的问题分解为许多较小、 较简单的问题， 使问题得以简化。 由于单个Agent解算能力有限， 难以完成复杂系统中的问题， 随后多智能体技术不断发展， 李伟等利用智能体技术在已有研究基础之上做出改进， 缩短决策时间， 相较于数学理论建模方法有较好的动态性［18］； 刘家义等利用多智能体系统（MAS）结合分布式多约束优化的思想解决了WTA的优化问题， 结合防空反导信息主导、 组网作战的特点， 创新性地将防空作战体系中各个作战实体设计为决策智能体、 武器智能体、 传感器智能体和拦截器智能体， 并改进加速梯队下降（Accelerated Gradient Descent， AGD）算法进行求解， 对于防空反导智能目标分配的发展研究起到促进作用［19］； 马悦等构建多智能体强化学习的协同目标分配模型， 聚焦于顶层分配策略的学习， 并采用Advantage Actor-Critic算法进行优化， 通过实验验证该方法能够实现大规模协同目标分配方案的动态生成［20］； 张杰等为解决分布式环境下多智能体系统的交互模型效率低、 局部冲突消解困难等问题， 设计了多主多从Stackelberg博弈的多智能体系统， 从多角度验证了模型的高效性和鲁棒性［21］； 赵鹏程针对空间众包中任务分配构建模型的局限性， 提出基于多智能体深度强化学习的模型来解决任务分配问题， 对武器目标分配有借鉴意义［22］。

通过分析， 目标分配模型由最初的静态模型逐渐向动态模型发展， 模型不断丰富， 但由于作战样式的快速发展， 模型研究的进展不能满足新型作战的需求， 主要表现在以下几个方面：

（1） 模型相对固化、 过度简化问题。 武器目标分配模型不是简单的数学模型， 而是借助数学手段构建的军事模型。 现有研究往往将此问题过度抽象简化为数学模型。 缺少对交战规则、 作战原则、 武器性能等约束条件的考虑， 导致模型的适用性差， 无法应对各种作战冲突。

（2） 现有研究中大部分模型是在完全信息条件下构建的， 假定防守方对攻击方的攻击信息无所不知， 并且忽略了传感器的配置， 在防空反导作战过程中传感器的准确性以及可靠性很大程度上影响目标分配效果， 通过传感器更新作战信息以及时推进更新策略的调整不失为提高模型动态性能的方法， 但对此方面的现有研究较少。

（3） 智能方法应用于军事领域是发展趋势， 但在智能目标分配的研究中仍存在一些问题： ①智能方法的训练数据不足， 缺少多样性， 数据库的数据质量和仿真环境的真实度关系智能体性能的优劣。 ②模型的可解释性和交互性弱， 指挥者对智能方法可信度低， 导致模型无法发挥其性能。 ③作为引导智能体趋于“智能”的奖励函数设计困难， 作战最终的胜利有时和作战过程中部分决策不相一致， 智能体的同一行动在不同作战背景下可能需要设计不同类型的奖励函数。 ④人工智能在游戏验证平台中取得显著突破， 但游戏平台和实际作战还有较大差距， 表现最突出的是实际作战中边界不确定， 这就给模型的构建带来复杂的因素， 包括环境、 人、 武器装备等。

1.3.2WTA算法发展情况

（1）  集中式求解算法

多階段匹配优化算法包括动态规划、 整数规划等。 Ahner等将作战任务分为两个阶段， 在动态规划框架内使用自适应规划算法， 并利用子梯度信息递归和CAVE函数逼近方法， 证明了算法在两阶段动态武器-目标分配中的最优性［23］； Camm等提出一种通过凸分段线性函数近似WTA问题的非线性问题， 降低计算难度［24］； OHanley等提出将WTA问题精确线性化的方法， 但是需要引入大量附加变量和约束条件， 难以解决大规模问题［25］。 Lu等不同于以往将WTA问题作为非线性模型的处理方法， 而是将问题描述为线性模型， 使用二进制线性规划， 通过列举法和分支定界技术求解该模型， 提出武器数量边界和武器支配新方法， 缩短执行时间， 同时可以精确解决有400个武器和400个目标的大规模目标分配问题， 为解决大规模的目标分配问题提供一定参考［26］； Andersen等为求解大规模问题， 提出一种精确求解方法， 即分支调整法。 该算法对现有的分支和边界算法进行优化， 通过实验进行验证， 该算法能处理1 500件武器和1 000个目标的大规模问题， 在求解问题的规模方面有较大提升［27］。

智能算法也称为元启发式方法。 其中遗传算法（GA）最早由Metler等提出用于解决对抗导弹威胁的WTA问题［28］； 王士同等提出基于遗传算法的动态武器目标分配策略DWTA-GA， 并通过实验证明其有效性［29］； 陶英歌等结合现代防空作战目标分配特点， 提出基于最大效益的目标分配模型， 利用遗传算法求解8个火力单元拦截8批来袭目标的作战问题， 证明该算法求解速度较快， 精度高［30］； 张晓丰等引入“优势”基因对标准遗传算法进行改进， 通过实例证明改进后的算法提高约60%的搜索效率［31］； 岳韶华等提出遗传蜂群算法， 将蜂群算法和遗传算法结合， 实现探索与开发的平衡， 兼顾了算法初期全局寻优和后期快速收敛的能力［32］。

粒子群算法的灵感源于鸟群觅食， 和遗传算法类似， 也采用“群体”和“进化”概念， 其通过个体间的协同与竞争， 实现复杂空间中最优解的搜索。 Zeng等首次将离散粒子群算法（DPSO）应用于求解武器目标分配问题中， 并在OPSO中引入贪婪搜索策略， 将置换的概念引入到更新策略中， 只要粒子在搜索空间中停滞， 就会被重新初始化， 一定程度上解决陷入局部最优问题［33］； 李欣然提出一种改进量子粒子群优化算法， 通过加入惯性变量使惯性权重具备自适应特点， 防止算法陷入局部最优［34］； 苏丁为等提出一种基于直觉模糊熵的改进粒子群算法， 采用一种交换操作和模拟退火机制对粒子群算法的局部最优解进行更新， 并根据直觉模糊熵值的大小对种群进行变异操作， 提高种群的多样性， 增加算法全局搜索能力［35］； Kong等提出一种基于学习策略的多目标粒子群优化算法（IMOPSO）。 为克服算法易陷入局部最优， 其通过建立模拟二元交叉和多项式变异的搜索策略， 增强了该算法的搜索能力， 实验表明具有较好的收敛性［36］。

由于各个算法都有其自身难以解决的缺点， 为了提高求解问题的能力， 许多学者将不同算法进行融合以弥补各算法的不足， 避免得到局部最优解， 或者求解效率不高等问题。 陈曼等设计了一种改善的混合粒子群优化算法， 引入了遗传算法中的杂交算子来解决此问题［37］； 邱少明等提出一种粒子多样性判别法， 通过求解粒子多样性贡献度， 用于混合量子行为粒子群和可调节遗传算法的粒子群迭代中， 避免早熟收敛， 具有较强的全局寻优能力［38］； Jiang等为提高目标分配效率， 提出了匈牙利融合遗传算法， 首先将匈牙利算法求解的可行解作为遗传算法初始种群的精英个体， 然后将分配模型中的目标函数作为适应度函数对结果进行优化， 既解决了匈牙利算法赋值结果不唯一的问题， 也优化了遗传算法易陷入局部最优的缺点， 并通过仿真实验验证了算法的有效性［39］。

（2）  分布式求解方法

基于市场机制的求解算法包括拍卖算法、 合同网等。 拍卖算法的本质是模拟人类拍卖活动的过程， 柳鹏等提出设立虚拟火力点和目标的方法对拍卖算法进行适当改进以解决目标分配问题［40］； 王增发等提出一种基于竞拍机制的战场目标分配方法， 兼顾目标分配的代价和作战效果， 能够在短时间内得出合理的分配方案［41］； 合同网是Smith于1980年提出的， 其思想源于人们在商务过程中用于管理商品和服务的合同机制（招标-投标-中标-签约）。 毛昭军等提出了一种在防空作战基于合同网协议的分布式目标分配算法， 通过对算法的实时性、 通讯量和优化程度进行比较， 证明了算法的有效性［42］； 唐苏妍等提出基于扩展合同网的动态目标分配算法， 相较于基本合同网的动态目标分配算法， 其更具有效性和优越性［43］。

智能算法包括人工鱼群算法、 蚁群算法等。 人工鱼群算法是一种利用鱼的三大基本行为（觅食、 聚群和追尾）进行寻优的优化算法。 林敏等采用人工鱼群算法对动态条件下武器目标分配问题进行求解， 并通过设计实例进行仿真实验， 验证了混沌人工鱼群算法在时间约束条件下相较遗传算法更具优越性［44］； 邵诗佳提出基于多目标人工鱼群算法的两阶段进化策略， 形成了新的状态更新规则， 在提高收敛速度的同时， 获得更好的解［45］。

蚁群算法于1992年由Marco Dorigo首次提出， 该算法来源于蚂蚁觅食行为。 蚂蚁在觅食过程中相互影响， 在爬行过程中通过信息素传递信息， 某一路径走过的蚂蚁越多， 后者选择此路径的可能性越大， 蚂蚁个体之间通过这种间接的通信机制实现协同搜索最短路径的目标， 以达到寻优的目的。 蚁群算法作为一种全局优化算法， 具有增强型学习效果好、 通用性强的优点。 范洁等提出混合蚁群算法求解WTA问题， 解决了蚁群算法求解速度过慢的缺点， 其首先通过遗传算法生成信息素的初始分布， 而后采用蚁群算法求精确解， 通过实验证明该算法在时间性上优于传统蚁群算法， 在求解精度上优于遗传算法［46］； 袁梅等采用信息素递减更新策略， 提高了收敛速度并缩短了求解时间［47］； 崔莉莉将蚁群算法与粒子群算法结合， 将粒子群算法中利用局部搜索和全局搜索经验对后继的粒子搜索进行指导的机制引入蚁群算法的信息素更新规则中， 提高算法的收敛效率， 并通过实验证明了此方法的可行性［48］； Hu等在空战背景下， 设计了改进蚁群优化算法（WIACO）， 提出基于优化的精英策略（Asrank）算法， 通过实验， 证明WIACO算法的迭代次数更少， 并且有效避免了局部最优［49］； Gao等将异构目标分为不同的目标类型， 与传统的蚁群算法相比， 将信息素分为隶属信息素和序列信息素， 以对应模型的分组排列特征， 不仅符合实际作战过程中目标的性能和异构特点， 在算法性能上也有较大提升， 且随着分配问题规模的扩大， 性能提升更加明显［50］；  Chen等提出新的信息素更新机制和新定义的启发式信息， 研究出一种多目标蚁群优化（MOACO）算法， 并在不同规模和实验背景下验证了该算法在收敛速度、 解质量和解多样性方面具有优越性［51］。

基于目前的算法研究， 主要集中于研究探索智能算法以及智能算法的混合优化算法， 以弥补各个算法的不足。 发展至今， 算法的寻优策略有了极大改进， 算法性能显著提升。 但是很多算法难以应用于武器装备， 主要表现在以下几个方面：

（1） 研究目的出现偏差。 现有研究主要目的是提升算法的寻优性能， 并且是在设定好的确定背景和数据环境下求解， 忽略了算法是否能够应用实际作战的根本问题。 军事作战过程是一个不确定过程， 人员、 武器、 环境随时可能发生难以预期的变化， 如在作战过程中突现的隐身目标、 超低空目标、 突分目标等冲突目标， 我方武器系统突遇故障或者被损， 敌方对我方武器系统施加强干扰等， 都可能导致算法瘫痪。 因此目标分配算法研究的首要目的不再单单是提高寻优性能， 而是寻求风险可控解， 提高在不确定环境下算法求解的宽容度， 确保在不确定风险环境下“有解”是首要任务。

（2） 算法设计脱离实际。 主要表现在两方面： 一方面忽略输出解的可行性， 即在求解时间内空袭态势的变化可导致输出解不符合当前目标的状态信息， 如图3所示。 现有方法主要通过提高初始解集合的质量或者改进寻优策略来提高算法求解效率， 但是在实际作战过程中， 无论求解速度如何提升， 模型输入和输出总会存在时间差， 并且随着空袭目标速度和机动能力的不断提升， 空袭态势变化程度不断加剧， 输出解与当前态势将会产生更加严重的冲突， 因此应寻求新的方法来提高输出解的可行性。 另一方面， 算法的变量设计存在问题， 实际作战问题中较多变量是有限测度和量化的“作战变量”， 但现有算法往往将变量定义为一个简单的技术或数学变量， 导致算法在底层设计过程中不符合实际作战逻辑。

（3） 算法边界不清晰。 现有研究主要验证其在既定背景下的最优性能， 但缺少边界测试， 以及一旦求解问题超出算法边界， 是否有相对较好的保底措施， 这些因素很大程度上降低了算法的可靠性， 使之无法应用于武器装备。

1.4WTA的作战应用

由于目标分配是指挥决策过程中的关键环节， 因此在进攻和防御的作战指挥决策过程中都被广泛应用。 在进攻作战中， 地对地打击、 空对地打击、 联合火力打击以及反舰、 反卫星都有极大的应用与发展； 在防御作战中， WTA的应用更加广泛和深入， 包括地面防空反导、 水面舰艇防空、 空中拦截等。

在防空反导作战过程中， 攻击方可根据防守方的防御资源快速、 机动、 灵活调配多种进攻力量， 而防空反导部队的火力单元机动能力相对较差、 资源配属相对固定， 如何利用现有的防空资源去抗击信息不完全的空袭体系， 特别是在攻防双方力量悬殊， 如（超）饱和攻击等战场态势下， 将现有的防空资源最大化利用显得尤为重要。 因此防空反导战术级指挥控制目标分配具有极大的研究和发展需求， 以应对现代化防空作战。

2存在问题

目标分配属于指挥控制流程中的核心环节， 其决策效能直接影响指挥质量和反应时间， 对于作战胜负起着至关重要的作用。 在分析目標分配问题国内外研究现状的基础上， 从攻防体系两个角度分析其理论研究在防空反导战术级指挥控制目标分配应用中存在的问题。

2.1空袭体系角度分析

（1） 针对逆梯度攻击的灵活性及适用性不足

在现代空防作战中， 空袭作战样式更加灵活多样， 空袭兵器性能不断提高， 采用“非线性作战方法”， 谋求作战的非对称优势和较高的作战效能， 而目前防空反导指挥控制系统目标分配模型还未达到真正意义上的动态分配， 大部分模型是基于已有场景构建的， 这就造成模型与作战目标脱离的情况较为严重， 导致理想化、 规则化的目标分配模型难以适应多变的战场环境。 在天基信息支持下的空袭作战中， 防空作战部署容易被敌方侦获， 进攻方不会在防守方设定好的作战背景下行动， 而是根据防空作战部署以及战法战术进行逆梯度攻击， 对防空体系造成严重威胁。 因此， 在防空反导战术级指挥控制决策系统中迫切需要具有高适应性的目标分配模型。

（2） 解决时空冲突的任务资源分配能力不足

从海湾战争到伊拉克战争， 多维空间联合空天进攻已是主要样式， 并更加注重将陆、 海、 空、 天、 电、 网多维空间的作战平台和资源通过信息系统为核心的网络化环境进行有机整合， 形成杀伤网（kill web）， 以“马赛克战”为代表的作战样式强调快速、 可伸缩、 自适应的联合多域杀伤力， 使之能够在多样化的作战环境中实施多样化的空袭行动， 并对防守体系造成了极大的威胁。 主要表现在两个方面： 一是战场态势单向透明， 借助雷达、 光电等传感器以及各种干扰方式， 扩大其认知域优势； 二是作战样式灵活多样， 致使防御难度大， 其利用平台优势， 可在平台上分布投放大量、 小型、 廉价以及多样的武器装备， 如巡航导弹、 无人机蜂群等， 增强其空袭的机动性和灵活性， 避免不同作战环境的限制。

空袭体系网络化能力的提升， 暴露出空防体系化作战能力的不足， 现有目标分配模型和算法难以在提升体系化作战能力方面有所贡献。 表现在两个方面： 一是大部分模型和算法不具备求解大规模目标分配的能力， 随着武器规模数量的提升， 求解效率下降明显； 二是部分模型和算法能够有效求解大规模武器系统的目标分配问题， 但仅考虑武器节点与目标节点的映射关系， 而真正的大规模目标分配不仅仅表现在武器系统数量规模， 大规模体系作战随之带来的是通信容量大、 武器节点类型多、 作战环路多。 在更加复杂的体系化作战场景下， 迫切需要模型和算法去解决多资源的时空冲突问题以及任务分配问题。

2.2防守体系角度分析

随着指挥控制系统的发展研究， 指挥控制模式由原有的手工指挥阶段， 经过半自动、 自动化指挥控制阶段， 向着智能化指挥控制阶段迈进， 人机关系也从指挥员决策、 机器辅助计算的方式向指挥员监督、 机器辅助决策的方式转变［52］。 其框架如图4所示。

为更好地发挥机器辅助决策优势， 需要处理好人机关系， 目前， 针对人机关系的处理存在以下问题。

（1） 人机交互能力差

防空反导作战中面临复杂的干扰环境及战场态势， 瞬息万变的战场态势留给指挥员决策处理的时间越来越少， 特别是在传统的战术级指挥控制目标分配模型中， 指挥员与计算机之间的任务分工较为模糊， 存在许多亟待解决的难点问题［53］， 如在作战过程中哪些是需要指挥人员干预的， 怎样干预， 干预的时机、 层次、 方式等， 使人员和机器无法利用各自优势充分发挥其作用， 导致两方面的问题： 一种情况是指挥员对系统利用度过高， 超出计算机的处理能力， 导致指挥员不能充分发挥自身的能动性， 过度依赖计算机的目标分配决策， 进行“流程式”作战， 导致误用； 另一种情况是没有充分利用机器擅长的能力， 极大浪费了机器的处理能力， 降低了人机系统的性能。 指挥员与决策系统之间的信任关系如图5所示， 以上两种情况都影响系统的整体作战能力［54］。

（2） 模型的可信度模糊

在作战过程中， 通过战术指揮控制目标分配自动决策辅助工具能够加快和加强决策过程， 人机系统可以应对更快的决策周期和大量的战场数据。 有效发挥系统性能的前提是指挥员需要对系统高度信任， 但在实际作战过程中， 指挥控制系统无法取得与之能力相匹配的信任度， 主要原因有两个方面： 一方面各种模型和算法在理论研究中大多验证其在理想情况下的最优性能， 指挥员无法掌握其对于处理边界和不确定因素的能力。 同时面对各种目标分配方法， 没有统一的评估体系去评估方法的性能和水平， 导致模型的性能无法量化评价［55］， 使指挥人员无法判断模型的水平， 这就造成了模型可信度无法衡量的问题。 另一方面， 对于指挥员来说， 机器系统就像一个黑匣子， 其单单注重信息的输入和结果的输出， 对分配的中间过程缺少直观形象的展示， 可解释性弱， 使指挥人员难以通过决策系统得出目标分配的分配依据、 分配过程、 考虑因素等， 导致模型的可信度不高［56］。

3发展需求

3.1综合集成分析、 建立高度智能的目标分配模块

防空作战中的指挥控制系统属于军事领域的复杂系统， 在目标分配决策过程中， 一方面需要考虑指挥员的经验知识与情感意志、 武器设备的工作状态、 空袭兵器的威胁程度、 敌方指挥人员的指挥习惯， 以及战场环境的地理、 气候、 水文、 社情等， 这些因素难以用现有的统计方法去量化表征； 另一方面需要针对多变的战场态势做出不同的反应， 将人的智慧与机器智能结合， 使之具有超强的自适应能力［57］。 而现有许多研究往往将目标分配问题设定为数学求解问题， 通过构建精确的数学模型和算法寻求分配策略最优解， 缺少将定性研究与定量研究、 宏观研究与微观研究、 经验知识与科学理论结合统一的过程， 从而造成了上述分析的诸多问题。 特别是在防空作战中， 我方临战时间仓促、 作战相对被动， 迫切需要构建新的模型框架去解决这些问题。

综合集成法可为解决此问题提供方向和思路， 其实质是通过将专家群体、 统计数据和信息资料三者有机结合， 构成一个高度智能化的人机交互系统， 其具体构成如图6所示。 随着不断丰富和发展， 借助智能Agent等技术形成多智能体技术、 分布式网络的研讨厅体系架构等。 现有目标分配智能化方法的研究也在不断深入， 但大部分是在传统模型的基础上借助机器学习手段进行智能优化， 没有上升到体系架构的智能化高度。 目标分配作为指挥控制系统的核心， 在指挥控制系统中发挥着至关重要的作用。 运用综合集成智能化理念， 使智能化目标分配实现感情的、 理性的、 经验的、 科学的、 定性的和定量的知识综合集成， 具备处理未来更加复杂的目标分配问题， 是智能化目标分配的发展需求。

3.2构建防空杀伤网、 建立基于“任务重心”的任务分配模式

在作战过程中， 防空部队运用各种侦察、 信息资源， 以构建自身的预警侦察系统和情报信息网络， 并有机融入预警侦察大系统， 同时预警探测、 识别跟踪、 拦截对抗等作战装备向着松耦合方向发展［58］， 各种作战资源实时共享， 各个作战节点各取所需， 打破了原有固化的资源配属关系， 将信息优势通过信息网络转化为行动优势和决策优势， 因此， 杀伤链-杀伤网［59］作战模式将逐渐取代传统目标分配模式， 杀伤网的构建如图7所示。 杀伤

链-杀伤网的信息共享、 各取所需的特点， 打破了捆绑的资源配属关系， 在一定程度上松懈了约束条件， 将火力单元从原有的固化关系中解放， 使其具备自任务、 自组织、 自适应能力， 跨越部门藩篱和上下级的指挥体制， 能够充分利用时间窗口， 适应防空反导作战特点， 极大增强了体系作战能力； 杀伤网作为一个类似万维网的作战网络， 每个武器节点不再受目标信息或制导信息的限制， 只要符合条件皆可参与作战， 同时其装备节点分布配置， 降低了节点受损而影响整体作战能力的风险［60］， 极大增强了指挥控制系统的韧性和弹性。 在防空作战中， 防空力量维持到作战结束， 在一定程度上就是胜利。 但现有防空反导目标分配模型还停留在武器-目标的分配关系上， 基于“任务重心”的网络化作战能力还远远不足［61］。

任务的分配理念可为杀伤链-杀伤网的资源及目标分配提供参考， 借助资源共享、 装备解耦、 体系紧耦的网络平台， 分配问题不再仅仅指武器和目标的分配， 而是基于任务规划出合适的作战资源抗击目标， 因为在杀伤网中， 构成一条杀伤链的侦察节点、 通信节点、 指挥控制节点、 打击节点有了更多的选择， 使任务分配有了更大的优化空间， 增强了作战的灵活性和抗击的可能性。

3.3 围绕实际作战需求、 建立符合作战逻辑的目标分配模型

随着实战化的迫切需求， 军事理论的研究要突出实战牵引。 提高作战指挥控制的自动化水平， 就要在研究中贴近实战环境、 考虑作战因素、 符合作战规则逻辑， 而不能仅仅追求模型和算法的理论性能， 要真正向可用于实战应用的方向发展 ［62］。

通过上述研究现状不难发现， 理论研究与实战应用脱节的情况较为严重， 实际作战中的目标分配决策绝不是仅依据目标函数进行简单的武器-目标关系配对， 而是要考虑复杂的现实因素。 指挥控制系统对来袭目标进行分配决策， 决策方案要确保武器系统能够执行， 使来袭目标能够进入火力通道，  继而才能对其进行打击。  在作战过程中， 首先要“能打”， 继而考虑“打好”， 但就目前的研究状况而言， 武器目标分配问题理论研究主要集中在模型和算法的优化， 关注的是如何又快又好地将目标与火力单元进行配对， 从而实现最大期望， 但忽视了分配过程要考虑的诸多基本因素， 缺少对作战逻辑模型的思考： 如来袭目标是否具有禁止分配标志； 相关火力单元是否有空闲的火力通道； 对于突现的高威胁目标是否要优先处理； 已分配的目标是否在对应武器系统的制导雷达扇区内或者可偏转角度内、 如果本级制导信息无法利用是否需要外部信息制导； 火力单元是否处于工作状态等诸多问题。 防空反导是一个高动态、 高实时、 多约束的作战过程， 因此应该充分考虑实际作战运用， 衡量“理论”和“应用”中的“度”， 找到“可行”和“优化”之间的“点”， 提高模型的实用性、 灵活性、 動态性和可扩展性， 使研究成果真正用于充满高不确定性风险的防空反导作战中。

4结论

随着战争形势的演变， WTA问题的发展研究要以实战应用为导向， 提高其智能化与网络化作战的能力， 让WTA问题的发展成果真正应用于作战并指导作战、 提高指挥自动化水平， 而不是仅仅停留在理论研究层面。

（1） 结合具体的兵种指挥控制系统（防空反导战术级指挥控制）对目标分配理论进行了研究， 详细阐述了目标分配的发展历程、 发展方向。

（2） 从理论研究、 实际应用等角度出发， 以攻防体系为切入点， 分析防空反导领域目标分配存在的针对逆梯度攻击的灵活性及适用性不足、 解决时空冲突的任务资源分配能力不足、 人机交互能力差、 模型的可信度模糊等问题， 为目标分配理论研究提供导向。

（3） 结合当前防空反导目标分配领域存在的问题， 提出了综合集成分析、 建立高度智能的目标分配模块， 构建防空杀伤网、 建立基于“任务重心”的任务分配模式， 围绕实际作战需求， 建立符合作战逻辑的目标分配模型， 为后续研究提供解决思路。

参考文献：

［1］ 孙立健， 周鋆， 余正飞.指挥与控制组织结构模型研究［J/OL］.系统工程理论与实践， 2022： 1-22.

Sun Lijian，  Zhou Yun，  Yu Zhengfei. Research on Organizational Structure Model of Command and Control ［J/OL］. Systems Engineering Theory and Practice，  2022： 1-22. （in Chinese）

［2］ 蔡怀平， 陈英武. 武器-目标分配（WTA）问题研究进展［J］. 火力与指挥控制， 2006， 31（12）： 11-15.

Cai Huaiping， Chen Yingwu. The Development of the Research on WeaponTarget Assignment（WTA） Problem［J］. Fire Control and Command Control， 2006， 31（12）：  11-15.（in Chinese）

［3］ 李勇君， 黄卓， 郭波. 武器-目标分配问题综述［J］. 兵工自动化， 2009， 28（11）： 1-4.

Li Yongjun， Huang Zhuo， Guo Bo. Review of WeaponTarget Assignment Problem［J］. Ordnance Industry Automation， 2009， 28（11）： 1-4. （in Chinese）

［4］ 韦刚， 高嘉乐， 孙文. 多目标-多武器系统目标分配模型与算法研究［J］. 飞航导弹， 2016（5）： 77-82.

Wei Gang， Gao Jiale， Sun Wen. Research on Target Assignment Model and Algorithm of MultiTargetMultiWeapon System［J］. Aerodynamic Missile Journal， 2016（5）：  77-82.（in Chinese）

［5］ 杨进帅， 李进， 王毅. 武器-目标分配问题研究［J］. 火力与指挥控制， 2019， 44（5）： 6-11.

Yang Jinshuai， Li Jin， Wang Yi. Study of Weapon Target Assignment Problem［J］. Fire Control & Command Control， 2019， 44（5）：  6-11.（in Chinese）

［6］ Kline A， Ahner D， Hill R. The WeaponTarget Assignment Problem［J］. Computers and Operations Research， 2019， 105（C）：  226-236.

［7］ 陆一平， 李慧慧. 静态武器目标分配问题的攻击界整数规划求解方法［J］. 系统工程理论与实践， 2019， 39（3）： 783-789.

Lu Yiping， Li Huihui. An AttackNumber Bounded Integer Programming Method for the Static WTA Problem［J］. Systems EngineeringTheory & Practice， 2019， 39（3）： 783-789.（in Chinese）

［8］ Li X Y， Zhou D Y， Yang Z， et al. A Novel Genetic Algorithm for the Synthetical SensorWeaponTarget Assignment Problem［J］. Applied Sciences， 2019， 9（18）：  68-69.

［9］ 韩松臣， 秦俊奇， 韩品尧， 等. 马尔可夫决策过程在目标分配中的应用［J］. 哈尔滨工业大学学报， 1996， 28（2）： 32-36.

Han Songchen， Qin Junqi， Han Pinyao， et al. An Application of the Markov Decision Process to Target Assignment［J］. Journal of Harbin Institute of Technology， 1996， 28（2）： 32-36.（in Chinese）

［10］ 张庆波， 周延延. 马尔可夫决策过程在防空系统目标分配中的应用［J］. 空军工程大学学报：自然科学版， 2001， 2（5）： 73-75.

Zhang Qingbo， Zhou Yanyan. An Application of the Markov Decision Process to the Target Assignment［J］. Journal of Air Force Engineering University： Natural Science Edition， 2001， 2（5）： 73-75.（in Chinese）

［11］ 蔡怀平， 刘靖旭， 陈英武. 动态武器目标分配问题的马尔可夫性［J］. 国防科技大学学报， 2006， 28（3）： 124-127.

Cai Huaiping， Liu Jingxu， Chen Yingwu. On the Markov Characteristic of Dynamic Weapon Target Assignment Problem［J］. Journal of National University of Defense Technology， 2006， 28（3）： 124-127.（in Chinese）

［12］ 柳毅， 佟明安. 匈牙利算法在多目標分配中的应用［J］. 火力与指挥控制， 2002， 27（4）： 34-37.

Liu Yi， Tong Mingan. An Application of Hungarian Algorithm to the MultiTarget Assignment［J］. Fire Control & Command Control， 2002， 27（4）： 34-37.（in Chinese）

［13］ 黄力伟， 许品刚， 王勤. 基于匈牙利算法求解的火力分配问题［J］. 火力与指挥控制， 2007， 32（6）： 25-28.

Huang Liwei， Xu Pingang， Wang Qin. Firepower Distribution Problems Based on Hungarian Method［J］. Fire Control and Command Control， 2007， 32（6）： 25-28.（in Chinese）

［14］ 殷红. 基于模糊匈牙利算法的炮兵火力单位分配问题［J］. 指挥控制与仿真， 2009， 31（3）： 26-28.

Yin Hong. Artillery Fire Units Distribution Based on Fuzzy Hungarian Method［J］. Command Control & Simulation， 2009， 31（3）： 26-28.（in Chinese）

［15］ 周洪喜， 张进， 彭晨远， 等. 基于匈牙利算法的多导弹阵地拦截指派规划［J］. 弹箭与制导学报， 2021， 41（4）： 79-84.

Zhou Hongxi， Zhang Jin， Peng Chenyuan， et al. Interception Assignment Planning of Multiple Missile Positions Based on Hunga￣rian Algorithm［J］. Journal of Projectiles， Rockets， Missiles and Guidance， 2021， 41（4）： 79-84.（in Chinese）

［16］ 张进， 郭浩， 陈统. 基于可适应匈牙利算法的武器-目标分配问题［J］. 兵工学报， 2021， 42（6）： 1339-1344.

Zhang Jin， Guo Hao， Chen Tong. WeaponTarget Assignment Based on Adaptable Hungarian Algorithm［J］. Acta Armamentarii， 2021， 42（6）： 1339-1344.（in Chinese）

［17］ 常雪凝， 石建迈， 陈超， 等.基于匈牙利-模拟退火算法的多阶段武器目标分配方法［J/OL］.系统工程与电子技术， 2022： 1-10.

Chang Xuening，  Shi Jianmai，  Chen Chao，  et al. MultiStage Weapon Target Assignment Method Based on HungarianSimulated Annealing Algorithm ［J/OL］. Systems Engineering and Electro￣nics， 2022： 1-10.（in Chinese）

［18］ 李伟， 康晓予， 赵晓哲. 基于多智能体的舰艇防空目标分配模型设计［J］. 军事运筹与系统工程， 2005， 19（3）：  30-33.

Li Wei， Kang Xiaoyu， Zhao Xiaozhe. Design of Warship Air Defense Target Assignment Model Based on MultiAgent［J］. Military Operations Research and Systems Engineering， 2005， 19（3）：  30-33.（in Chinese）

［19］ 刘家义， 王刚， 张杰， 等. 基于改进AGD-分布式多智能体系统的目标优化分配模型［J］. 系统工程与电子技术， 2020， 42（4）： 863-870.

Liu Jiayi， Wang Gang， Zhang Jie， et al. Target Optimal Assignment Model Based on Improved AGDDistributed MultiAgent System［J］. Systems Engineering and Electronics， 2020， 42（4）：  863-870.（in Chinese）

［20］ 马悦， 吴琳， 许霄.基于多智能体强化学习的协同目标分配［J/OL］.系统工程与电子技术， 2022： 1-12.

Ma Yue，  Wu Lin，  Xu Xiao. Collaborative Goal Assignment Based on MultiAgent Reinforcement Learning ［J/OL］. Systems Engineering and Electronics， 2022： 1-12.（in Chinese）

［21］ 張杰， 岳韶华， 王刚， 等. 基于Stackelberg与边拉普拉斯矩阵的多智能体系统［J］. 计算机科学， 2021， 48（8）：  253-262.

Zhang Jie， Yue Shaohua， Wang Gang， et al. MultiAgent System Based on Stackelberg and Edge Laplace Matrix［J］. Computer Scien￣ce， 2021， 48（8）：  253-262.（in Chinese）

［22］ 赵鹏程， 高尚， 于洪梅. 基于多智能体深度强化学习的空间众包任务分配［J］. 吉林大学学报： 理学版， 2022， 60（2）：  321-331.

Zhao Pengcheng， Gao Shang， Yu Hongmei. Spatial Crowdsourcing Task Assignment Based on MultiAgent Deep Reinforcement Learning［J］. Journal of Jilin University： Science Edition， 2022， 60（2）： 321-331.（in Chinese）

［23］ Ahner D K， Parson C R. Optimal MultiStage Allocation of Wea￣pons to Targets Using Adaptive Dynamic Programming［J］. Optimization Letters， 2015， 9（8）： 1689-1701.

［24］ Camm J D， Norman S K， Polasky S， et al. Nature Reserve Site Selection to Maximize Expected Species Covered［J］. Operations Research， 2002， 50（6）：  946-955.

［25］ OHanley J R，  Scaparra M P，  García S. Probability Chains： A General Linearization Technique for Modeling Reliability in Facility Location and Related Problems［J］. European Journal of Operational Research， 2013， 230（1）： 63-75.

［26］ Lu Y P， Chen D Z. A New Exact Algorithm for the WeaponTarget Assignment Problem［J］.OmegaInternational Journal of Management Science， 2021.

［27］ Andersen A C， Pavlikov K， Toffolo T A M. WeaponTarget Assignment Problem： Exact and Approximate Solution Algorithms［J］. Annals of Operations Research， 2022， 312（2）： 581-606.

［28］ Metler W A， Preston F L， Hofmann J. A Suite of Weapon Assignment Algorithms for a SDI MidCourse Battle Manager［R］. 1990.

［29］ 王士同， 劉征. 动态武器目标分配问题的DWTA-GA算法［J］. 华东船舶工业学院学报， 1999， 13（5）： 17-22.

Wang Shitong， Liu Zheng. DWTAGA Algorithm for the Dynamic Weapen Target Assignment Problem［J］. Journal of East China Shipbuilding Institute， 1999， 13（5）： 17-22.（in Chinese）

［30］ 陶英歌， 郭乃林. 基于遗传算法的目标分配优化模型研究［J］. 现代防御技术， 2003， 31（1）： 21-24.

Tao Yingge， Guo Nailin. Research on the Optimization Model of Target Assignment Based on GA［J］. Modern Defense Technology， 2003， 31（1）： 21-24.（in Chinese）

［31］ 张晓丰， 程红斌， 张凤鸣. 改进遗传算法的导弹目标分配方法［J］. 火力与指挥控制， 2007， 32（4）： 59-61.

Zhang Xiaofeng， Cheng Hongbin， Zhang Fengming. A Method for Missile Target Assignment Based on the Improved GA［J］. Fire Control and Command Control， 2007， 32（4）： 59-61. （in Chinese）

［32］ 岳韶华， 何晟， 王刚， 等. 基于改进遗传蜂群算法的武器系统优化部署问题研究［J］. 兵器装备工程学报， 2022， 43（8）： 80-86.

Yue Shaohua， He Sheng， Wang Gang， et al. Optimization of Weapon System Deployment Based on Improved Genetic Bee Colony Algorithm［J］. Journal of Ordnance Equipment Engineering， 2022， 43（8）： 80-86.（in Chinese）

［33］ Zeng X P， Zhu Y L， Nan L， et al. Solving WeaponTarget Assignment Problem Using Discrete Particle Swarm Optimization［C］∥the 6th World Congress on Intelligent Control and Automation， IEEE， 2006： 3562-3565.

［34］ 李欣然. 改进量子行为粒子群算法求解武器目标分配问题［J］. 计算机系统应用， 2013， 22（7）： 137-140.

Li Xinran. QuantumBehaved Particle Swarm Algorithm on Wea￣pon Target Assignment［J］. Computer Systems & Applications， 2013， 22（7）： 137-140.（in Chinese）

［35］ 苏丁为， 王毅， 周创明. 基于直觉模糊熵的改进粒子群算法求解WTA问题［J］. 计算机科学， 2016， 43（12）： 255-259.

Su Dingwei， Wang Yi， Zhou Chuangming. Improved Particle Swarm Optimization Algorithm for Solving WeaponTarget Assignment Problem Based on Intuitionistic Fuzzy Entropy［J］. Computer Science， 2016， 43（12）： 255-259.（in Chinese）

［36］ Kong L R， Wang J Z， Zhao P. Solving the Dynamic Weapon Target Assignment Problem by an Improved Multiobjective Particle Swarm Optimization Algorithm［J］. Applied Sciences， 2021， 11（19）： 9254.

［37］ 陳曼， 周凤星. 改进粒子群算法的舰载武器目标分配［J］. 火力与指挥控制， 2018， 43（11）： 72-76.

Chen Man， Zhou Fengxing. Shipborne Weapon Target Assignment Based on Improved Particle Swarm Optimization［J］. Fire Control & Command Control， 2018， 43（11）： 72-76.（in Chinese）

［38］ 邱少明， 冯江惠， 杜秀丽， 等. 基于改进多目标HQPSOGA求解武器目标分配问题［J］. 计算机应用与软件， 2021， 38（11）： 255-262.

Qiu Shaoming， Feng Jianghui， Du Xiuli， et al. Weapon Target Assignment Based on Improved MultiObjective HQPSOGA［J］. Computer Applications and Software， 2021， 38（11）： 255-262.（in Chinese）

［39］ Jiang Y， Wang D B， Bai T T， et al. MultiUAV Objective Assignment Using Hungarian Fusion Genetic Algorithm［J］. IEEE Access， 2022， 10： 43013-43021.

［40］ 柳鹏， 高杰， 刘扬. 基于拍卖算法的目标分配问题优化［J］. 兵工自动化， 2008， 27（9）： 22-24.

Liu Peng， Gao Jie， Liu Yang. Target Distribution Optimization Based on Auction Algorithm［J］. Ordnance Industry Automation， 2008， 27（9）： 22-24.（in Chinese）

［41］ 王增发， 徐克虎， 孔德鹏. 基于竞拍机制的复杂环境目标分配法［J］. 中国科技信息， 2017（7）： 68-69.

Wang Zengfa， Xu Kehu， Kong Depeng. Target Allocation Method for Complex Environment Based on Auction Mechanism［J］. China Science and Technology Information， 2017（7）： 68-69.（in Chinese）

［42］ 毛昭军， 李云芝， 蔡业泉. 防空作战中合同网协议分布式目标分配算法［J］. 火力与指挥控制， 2008， 33（1）： 90-93.

Mao Zhaojun， Li Yunzhi， Cai Yequan. Distributed WeaponTargetAssignment（WTA） Algorithm Based on Contract Net Protocol（CNP） in AntiAir Warfare［J］. Fire Control and Command Control， 2008， 33（1）： 90-93.（in Chinese）

［43］ 唐苏妍， 梅珊， 朱一凡， 等. 基于扩展合同网协议的分布式武器目标分配方法［J］. 系统工程与电子技术， 2011， 33（3）： 568-574.

Tang Suyan， Mei Shan， Zhu Yifan， et al. Distributed Weapon Target Assignment Algorithm Based on Extended Contract Net Protocol［J］. Systems Engineering and Electronics， 2011， 33（3）： 568-574.（in Chinese）

［44］ 林敏， 王成飞. 动态WTA问题的混沌人工鱼群算法［J］. 指挥控制与仿真， 2014， 36（5）： 63-66.

Lin Min， Wang Chengfei. Dynamic Weapon Target Assignment Method Based on Chaotic Artificial Fish Swarm Algorithm［J］. Command Control & Simulation， 2014， 36（5）： 63-66.（in Chinese）

［45］ 邵诗佳. 基于智能算法的武器目标分配问题研究［D］. 哈尔滨： 哈尔滨工程大学， 2019.

Shao Shijia. Research on Weapon Target Assignment Based on Intelligent Algorithm［D］. Harbin： Harbin Engineering University， 2019. （in Chinese）

［46］ 范潔， 刘玉树， 龚元明， 等. 基于混合蚁群算法的WTA问题求解［J］. 计算机工程与应用， 2005， 41（10）： 59-61.

Fan Jie， Liu Yushu， Gong Yuanming， et al. A Commingled Ant Colony Optimization Algorithm for Solving WTA Problem［J］. Computer Engineering and Applications， 2005， 41（10）： 59-61.（in Chinese）

［47］ 袁梅， 凌明祥， 曾庆双. 基于信息素递减的蚁群算法的WTA问题求解［J］. 计算机仿真， 2008， 25（2）： 23-25.

Yuan Mei， Ling Mingxiang， Zeng Qingshuang. An Ant Colony Algorithm Based on Pheromone Declining for Solving the WTA Problem［J］. Computer Simulation， 2008， 25（2）： 23-25.（in Chinese）

［48］ 崔莉莉. 基于蚁群算法的武器-目标分配问题研究［D］. 上海： 上海交通大学， 2011.

Cui Lili. Research on WeaponTarget Assignment Based on Ant Colony Algorithm［D］. Shanghai： Shanghai Jiao Tong University， 2011. （in Chinese）

［49］ Hu X W， Luo P C， Zhang X N， et al. Improved Ant Colony Optimization for WeaponTarget Assignment［J］. Mathematical Problems in Engineering， 2018： 1-14.

［50］ Gao S， Wu J Z， Ai J L. MultiUAV Reconnaissance Task Allocation for Heterogeneous Targets Using Grouping Ant Colony Optimization Algorithm［J］. Soft Computing， 2021， 25（10）： 7155-7167.

［51］ Chen L Z， Liu W L， Zhong J H. An Efficient MultiObjective Ant Colony Optimization for Task Allocation of Heterogeneous Unmanned Aerial Vehicles［J］. Journal of Computational Science， 2022， 58： 101545.

［52］ 孙涛， 龙庆华， 巢育龙， 等. 防空反导雷达高作战效能人机系统设计方法［J］. 现代防御技术， 2022， 50（4）： 107-115.

Sun Tao， Long Qinghua， Chao Yulong， et al. Design Method of ManMachine System with High Operational Efficiency for Air Defense and AntiMissile Radar［J］. Modern Defence Technology， 2022， 50（4）： 107-115.（in Chinese）

［53］ 罗建平， 刘岗， 陈超， 等. 防空指挥控制系统人机交互设计趋势研究［J］. 包装工程， 2020， 41（24）： 40-45.

Luo Jianping， Liu Gang， Chen Chao， et al. HumanComputer Interaction Design Process of Air Defense Command and Control System［J］. Packaging Engineering， 2020， 41（24）： 40-45.（in Chinese）

［54］ 付亚芝， 郭进利. 基于非合作博弈的动态人机系统功能分配法［J］. 火力与指挥控制， 2021， 46（2）： 30-34.

Fu Yazhi， Guo Jinli. A Dynamic Method of ManMachine System Function Allocation Based on NonCooperative Game Theory［J］. Fire Control & Command Control， 2021， 46（2）： 30-34.（in Chinese）

［55］ 于小岚， 熊伟， 韩驰， 等.天基信息支援装备体系作战效能评估方法研究［J/OL］.系统仿真学报， 2022： 1-15.

Yu Xiaolan，  Xiong Wei，  Han Chi，  et al. Research on Combat Effectiveness Evaluation Method of SpaceBased Information Support Equipment System ［J/OL］. Journal of System Simulation， 2022： 1-15.（in Chinese）

［56］ 王特， 沈阳， 王九龙， 等. 智能指挥信息系统作战效能评估研究［C］∥第十届中国指挥控制大会论文集（上册）. 北京， 2022：  384-387.

Wang Te，  Shen Yang， Wang Jiulong，  et al. Research on Combat Effectiveness Evaluation of Intelligent Command Information System ［C］∥Proceedings of the 10th China Command and Control Conference （Volume 1），  2022： 384-387.（in Chinese）

［57］ 付强， 王刚， 范成礼， 等. 防空反导智能指控系统作战需求研究［J］. 火力与指挥控制， 2020， 45（2）： 28-31.

Fu Qiang， Wang Gang， Fan Chengli， et al. Research on Combat Demand of Air Defense AntiMissile Intelligent Command and Control System［J］. Fire Control & Command Control， 2020， 45（2）： 28-31.（in Chinese）

［58］ 杨国利， 李云龙， 王宁. 网络化作战体系关键目标打击筹划研究［J］. 指挥与控制学报， 2020， 6（2）： 147-156.

Yang Guoli， Li Yunlong， Wang Ning. Attack Planning for Key Targets in Networked Operation System of Systems［J］. Journal of Command and Control， 2020， 6（2）： 147-156.（in Chinese）

［59］ 謝宇鹏， 侯学隆， 王宗杰， 等. 马赛克作战概念下多无人机网络化作战效率评估［J］. 战术导弹技术， 2022（4）： 196-202.

Xie Yupeng， Hou Xuelong， Wang Zongjie， et al. Efficiency Eva￣luation of MultiUAV Network Operation under Mosaic Operation Concept［J］. Tactical Missile Technology， 2022（4）： 196-202.（in Chinese）

［60］ 陈登， 陈楚湘， 周春华. 基于“OODA环”的杀伤网节点重要性评估［J/OL］.兵工学报， 2022： 1-11.

Chen Deng，  Chen Chuxiang，  Zhou Chunhua. Importance Evaluation of Kill Network Nodes Based on “OODA Ring” ［J/OL］. Acta Armamentarii， 2022： 1-11.（in Chinese）

［61］ Chen W H， Li J C， Jiang J. Heterogeneous Combat Network Link Prediction Based on Representation Learning［J］. IEEE Systems Journal， 2021， 15（3）：  4069-4077.

［62］ 张家瑞， 王刚， 王思远. 防空反导战术级指控系统体系架构研究［J］. 火力与指挥控制， 2021， 46（1）： 9-13.

Zhang Jiarui， Wang Gang， Wang Siyuan. Research on the Architecture of Air and Missile Defense of TacticsLevel Command and Control System［J］. Fire Control & Command Control， 2021， 46（1）：  9-13.（in Chinese）

Research on Target Assignment Development of Air Defense and AntiMissile Tactical Command and Control System

Liu Xiangyu1， 2，  Wang Gang1*， Li Tengda1， 2， Xia Zhiquan3

（1.Air and Missile Defense College， Air Force Engineering University， Xian  710051， China；2. Graduate College， Air Force Engineering University， Xian  710051， China；3. Unit 93126 of PLA， Beijing 100038， China）

Abstract： Target assignment is the core of command and control decisionmaking stage. Many scholars have done a lot of research on target assignment problem，  and made great progress in target assignment model and algorithm. However， with the evolution and development of new combat styles such as Mosaic warfare， distributed warfare and networkcentric warfare， the complexity of modern air defense operations has increased unprecedentedly. In view of the problems of air defense and antimissile tactical target assignment，  such as weak adaptability to different combat scena￣rios，  lack of game antagonism and robustness， etc.，  by summarizing and sorting out the research status of target assignment，  the challenges faced by the theoretical research of target assignment in the application process of air defense and antimissile operations are deeply discussed from the perspective of the development of offensive and defense systems. This paper answers the root causes of many problems in the tactical target allocation of air defense and missile defense，  and puts forward the development needs of intelligent，  networked and real combat target allocation in view of the deficiencies.

Key words： target assignment； air defense and antimissile； humancomputer interaction； kill web； tactical;  command and control system