一种SAR回波历程快速实时计算方法

邢晨 潘明海

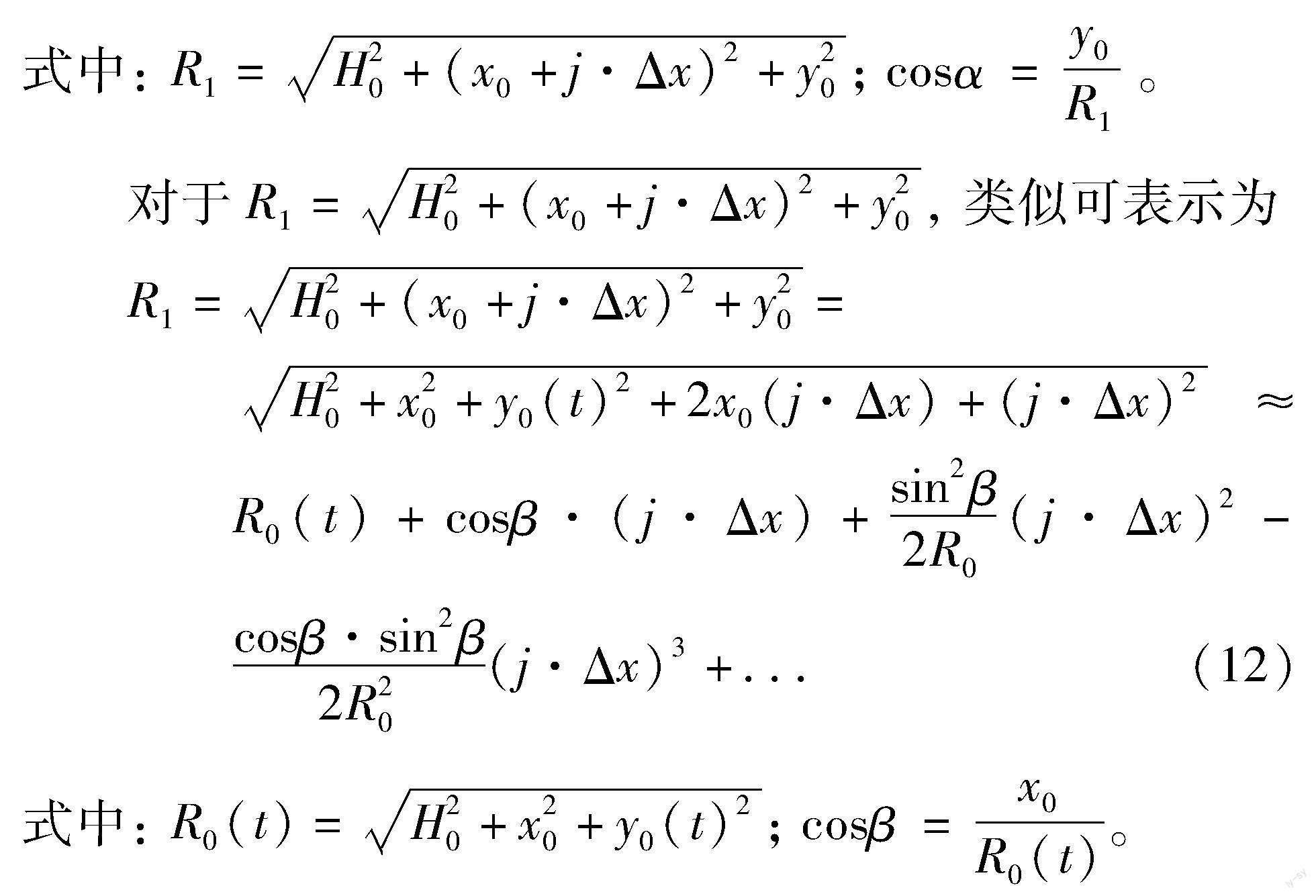
摘要：      针对合成孔径雷达（Synthetic Aperture Radar， SAR）目标回波模拟计算量过大的问题， 采用两次多阶泰勒级数展开对回波系统函数中的距离历程进行计算， 并结合数据外推的方法完成距离历程的快速实时计算。 该方法使用多次乘法和加法代替计算量较大的开方运算， 可保证在一定计算精度的前提下提高距离计算的实时性， 同时结合距离历程模型的规律性， 采用数据外推代替重复的计算过程， 进一步降低计算量， 提高实时性。 通过仿真对比不同阶数泰勒级数展开在同一距离处的计算误差， 得到了4阶为该仿真条件下的最优泰勒展开阶数，  最后分别对9个分布密集的点目标和真实场景目标进行回波模拟和成像。 点目标仿真结果表明， 该方法在不影响回波信号性能的前提下可以使生成回波信号的时间减少53%， 速度提升2倍； 真实场景仿真结果表明， 该方法可以应用于大场景的回波模拟。

关键词：     回波模拟； 回波系统函数； 实时计算； 距离历程； 数据外推； 点目标； SAR

中图分类号：     TJ760; TN95    文章编号：     1673-5048（2023）04-0098-08

文献标识码：    A    DOI： 10.12132/ISSN.1673-5048.2022.0269

0引言

合成孔径雷达（Synthetic Aperture Radar， SAR）是一种能实现高分辨、 远距离、 广范围的成像雷达［1］， 具有很高的应用价值， 是目前雷达的主要成像方式。

随着真实的雷达图像分辨率不断提高， 对模拟图像分辨率的要求也越来越高［2］， 研究人员普遍开始采用基于电磁计算的雷达成像仿真技术［3-4］， 但这种计算量是相当大的， 一般需要通过数字信号处理器（Digital Signal Processor， DSP）、 现场可编程逻辑门阵列（Field Programmable Gate Array， FPGA）等硬件加速来保证实时性［5-7］。 此外， 图形处理器（Graphics Processing Unit， GPU）由于多核多线程的特性被广泛应用于SAR回波模拟中。 早在2009年， 意大利萨勒诺大学的Clemente等人利用计算统一设备架构（Compute Unified Device Architecture， CUDA）编程平台， 在Nvidia Tesla C1060显卡上实现了SAR回波模拟［8］。 同年， 文献［9］利用中央处理器（Central Processing Unit， CPU）和GPU混合编程实现了SAR的面目标回波模拟。 目前， 国内大部分研究已经在GPU上实现了回波模拟算法的并行化， 但是其采用的回波模拟算法大多是传统的回波模拟算法， 在仿真大场景时依然存在效率较为低下的问题， 有进一步的加速空间。 为了实现实时计算， 文献［10］提出了等距离环的概念， 对成像场景进行等距分割， 并使用多个FPGA并行计算； 文献［11］通过使用宽带数字射频存储器（Digital Radio Frequency Memory， DRFM）技术和并行计算技术实现了较小延迟的SAR回波計算和生成。 即使在硬件平台上进行回波模拟， 仍存在模拟点数过多和系统函数计算量过大的问题， 当前大多数研究围绕在如何减少模拟点数， 针对SAR合成孔径的特性， 越来越多的研究采用子孔径处理［12-17］进行回波模拟， 通过在回波信号方位向划分子孔径， 分段处理， 一定程度上解决了模拟点数过多的问题， 而对系统函数计算量的研究数量不多。

距离历程是回波系统函数中的一个重要参数， 针对回波系统函数计算量过大的问题， 本文提出使用多阶泰勒级数展开对距离历程进行计算， 在保证一定精度的前提下提高距离计算的实时性， 通过对不同阶数泰勒级数展开产生的计算误差进行仿真对比， 找出最优泰勒级数展开阶数， 并从理论上分析了距离历程模型的规律性， 提出存储部分数据来代替重复计算， 进一步减少计算量。

1SAR目标回波信号模型

1.1SAR空间几何模型

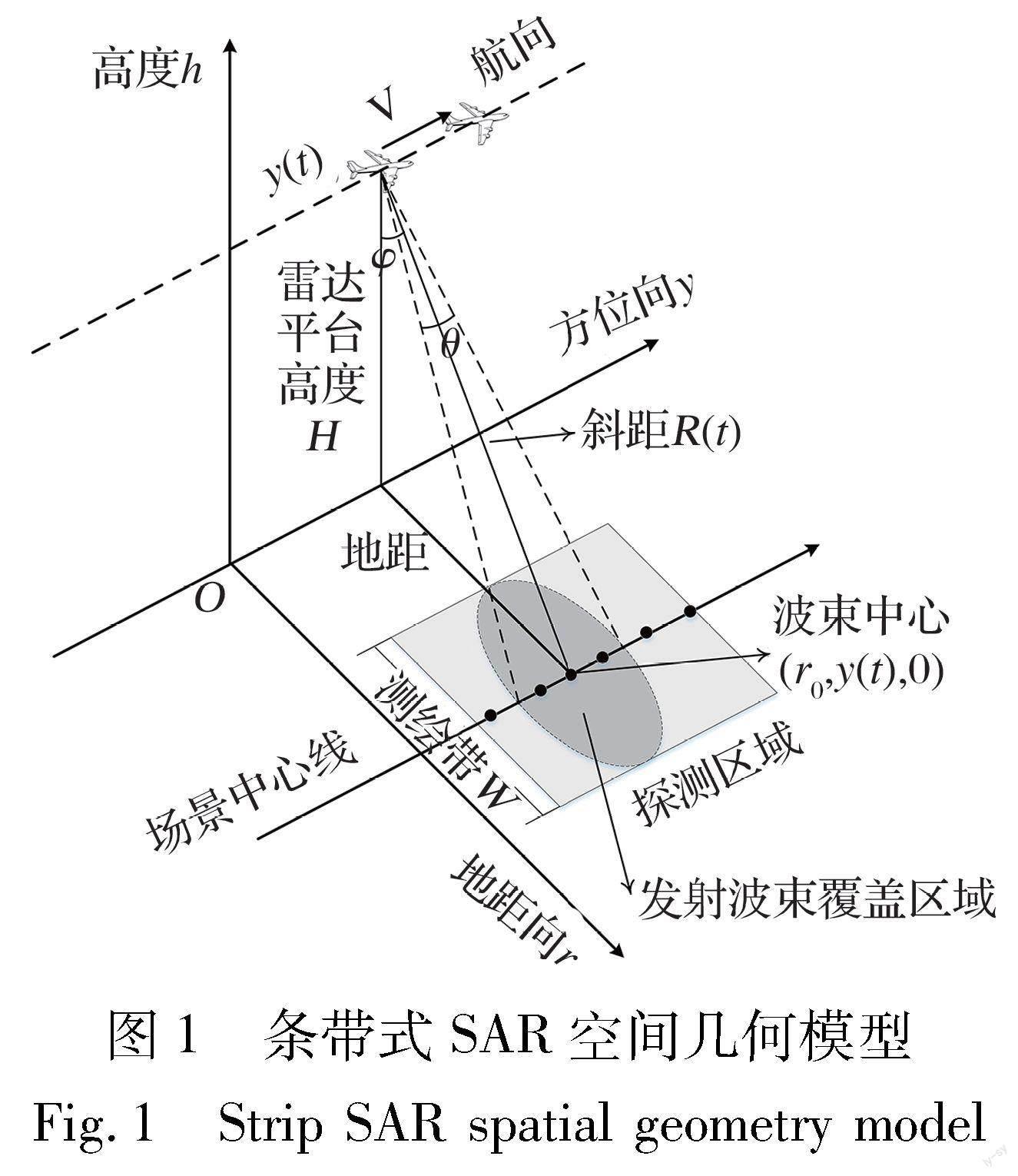
SAR的回波信号是雷达平台在各个时刻发射波束覆盖范围内每个点目标回波信号的叠加。 图1是条带式SAR的空间几何模型， 选取直角坐标系为参考坐标系， rOy为地平面， 假设雷达平台高度为H， 沿方位向y正方向以速度V匀速飞行， 机载平台向航向正侧方向地面发射电磁波， 俯仰角度为φ， t时刻平台坐标为（0， y（t）， H）， rOy平面上波束中心坐标为（r0， y（t）， 0）， 波束宽度为θ， 波束照射区域为阴影部分， 测绘带宽度为W。

1.2目标回波信号模型

假设雷达平台发射的脉冲串为

式中： rect［·］为矩形函数； Tp为发射信号的脉冲宽度； fc为载频； k为调频斜率。

假设（ri， yi，0）为探测区域内任一散射点， 由图1可得， 该点与雷达平台的瞬时斜距为

式中： t为慢时间； ta为快时间； A为接收信号的幅度因子， 与目标的后向散射系数和天线方向图有关； c为光速。

解调去掉载波后， 点目标的回波信号可以写为

式中： 第一个指数项为多普勒分量， 是回波信号的方位向相位； 第二个指数项为基带LFM的延迟分量。

实际上， 真实场景的目标是由地面大量散射点组成， 对于真实场景的模拟中， 把每个散射点当成一个单点目标考虑， 整个场景的目标回波可以看作所有散射点回波的叠加， 则真实场景回波信号模型可表示为

式中： L为场景中散射点的总个数； Ak为第k个散射点回波的幅度因子； Rk（t）为第k个散射点在t时刻的瞬时斜距。

2SAR目标回波系统函数的实时计算

2.1SAR目标回波系统函数模型

SAR目标回波是雷达照射波束内全部散射点回波的叠加， 可以看作是雷达发射信号经过一个系统后的输出。 因而SAR目标回波可表示为雷达发射脉冲s（t）与目标回波系统函数h（t）的卷积， 即

sr（t）=s（t）h（t） （7）

式中： 回波系统函数h（t）包含波束照射范围内所有散射点回波的延迟、 幅度以及方位相位等信息， 可表示为

由式（8）可知， 目标回波系统函数是一系列冲激函数的叠加， 这些冲激函数具有不同的延时、 幅度和相位， 其作用就是对雷达发射信号进行延迟、 幅度和相位的调制。 在距离时域脉冲相干法中， 将根据目标回波系统函数的采样周期对散射点的延迟进行近似处理。 此时在某个采样时刻的回波系统函数将是落入该时刻所代表距离门的所有散射点信息的叠加， 即

式中： M为落入该距离门散射点的个数； Ak， Rk和tk分别为该距离门内第k个散射点回波的幅度、 距离和延迟； Ts为系统函数的采样周期。

由于雷达波束在地面照射范围内的散射点數目非常多， 因而在SAR目标回波仿真中， 回波系统函数的计算量将非常大。

2.2高实时性距离历程的计算方法

2.2.1基于多阶泰勒级数展开的距离历程模型

回波系统函数主要是计算每个散射点的距离， 根据距离可以确定回波相位以及该散射点所处的距离门， 最后对处于同一个距离门的目标信息进行累加。 因此， 距离历程是回波系统函数的一个重要参量。

以等距离环和方位向分辨单元对目标场景进行网格化处理， 场景中散射点的瞬时斜距模型， 如图2所示。

设SAR雷达高度为H0， t时刻波束中心的坐标为（x0， y0（t）， 0）， 则雷达发射波束覆盖区域内某个散射点（i， j）的瞬时斜距为

式中： Δx和Δy分别为地面上相邻散射点在距离向和方位向的分辨间隔； i和j分别为目标区域中散射点位于第i个距离环（距离向分辨单元）和位于第j个方位向分辨单元， 即i和j可表示散射点的行列号。

由式（10）可见， 传统的距离计算方法存在两个缺点： （1）使用开方进行计算， 开方运算具有很大的计算量， 且不便于FPGA等硬件平台实现， 不利于成像目标回波的实时计算； （2）通常H0， x0两个参数的数值会很大， 会导致每次计算的距离数值过大。

为了便于目标回波实时计算， 本文提出采用多阶泰勒级数展开对式（10）进行计算， 使用多个乘法和加法来代替开方计算。 考虑到某一行目标数量通常比某一列目标数量多， 首先对于中心列的散射点进行泰勒级数展开。 对于某一列目标， 其行号都相同， 视（i·Δy）为一个整体进行多阶泰勒级数展开， 则式（10）可表示为

R0（t）为雷达平台到波束中心点的斜距， 通过对距离历程模型进行多阶泰勒级数展开， 这个数值最大的参数被分离， 可以作为一个常数来处理， 只需要计算泰勒展开项的各次幂和各次幂的系数即可， 避免了大数值参数的重复计算。

此外， 由于雷达载波信号的波长很短， 因而散射点距离的计算必须保持很高的精度， 以保证回波信号相位的计算精度， 这便为式（11）～（12）中泰勒级数展开所取的阶数提出了一定的要求， 仿真时需要根据具体的参数选取最优泰勒级数展开阶数。

2.2.2距离历程模型的规律性

假设SAR目标模拟器数据参数更新周期为T， T=Δy/v， 表示每当雷达平台移动一个方位分辨单元的距离， 数据更新一次， 则t时刻与经历多个T后某等距离环中心处各等效散射点的距离变化， 如图3所示。

对于任意t+m·T时刻， （i+m，j）处等效散射点的距离如式（13）所示， 其与t时刻（i，j）处等效散射点的距离完全一致：

由于i， j， t， m均是随机取值， 故式（13）具有普遍性， 可以得到

R（i， j， t）=R（i+m， j， t+m·T）（14）

式中： 0≤t

利用R（i，j，t）的规律性， 采用数据外推的方法对距离历程进行实时计算： 首先将t∈［0，T）内所有发射波束覆盖范围内各散射点的距离数据按脉冲编号存储起来， 在后续周期中按照脉冲在该周期中的编号直接调用所需的数据， 以此来代替每个周期都对覆盖范围内各散射点进行距离计算， 可以减少大量的重复操作。 此方法以一定的存储器资源为代价， 大大降低了运算量， 在存储器资源足够的情况下， 对于距离历程以及回波系统函数的实时计算有很大的帮助。

2.3系统函数的实时计算

散射点回波方位向相位表达式为

利用FPGA计算回波相位时， 三角函数的计算需要利用查表的方法来实现， 所以相位计算将转换为计算相位查询表的地址。

文中使用两次多阶泰勒级数展开计算各散射点距离， 两次展开的实现方式分别如下：

（1） 首先计算中心行目标距离及相关信息。 根据泰勒级数展开公式， 可得各目标相对于波束中心点的相对距离表达式为

R1=R0+k1·C1+k2·C2－k3·C3+…（16）

式中： C1， C2， C3， …为泰勒展开项的各次幂； k1， k2， k3， …为展开式中各次幂的系数的分子部分。

各参数表达式为

由于x0， y0， H0， Δy均为定值， 所以式（17）中的所有参数均为定值， 可以直接从上位机中获取。

以4阶泰勒展开级数为例， 假设中心行网格数为L， 则计算中心列目标距离信息需要（4*L）次乘法和（4*L）次加法运算。

（2） 对于某一列目标， 只计算其到该列中心行目标的相对距离即可， 即

式中： D1， D2， D3等参数为定值， 将存储在硬件中， 而l1， l2， l3， N1， N2， N3等参数则由DSP板负责计算。

l1， l2， l3， N1， N2， N3计算公式如下：

由于l2中包含1， 所以l2·D2可以化简为D2-lp2·D2， 减少一个乘法器的消耗。

同样地， 以4阶泰勒级数展开为例， 假设列网格数为Q， 计算每列目标的相对距离信息需要（9*Q）次乘法和（8*Q）次加法运算， 除法运算由移位寄存器完成。

对单个发射脉冲覆盖范围内所有散射点， 计算距离需要（9*Q+4*L）次乘法和（8*Q+4*L）次加法运算。

假设回波模拟过程中， 共发射N个脉冲， 且［0，T）内发射M（N=k·M， k为整数）个脉冲， 则回波模拟过程中距离计算部分共需要（9*Q+4*L）*N次乘法和（8*Q+4*L）*N次加法运算， 而利用式（14）进行数据外推后， 仅需要（9*Q+4*L）*M次乘法和（8*Q+4*L）*M次加法运算， 为原来计算量的1/k。

对于各目标的相位信息， 需要计算的部分为

式中： Z0=2n（n为整数）; Z=1 024。

选取合适的Z0， 使得Rλ的分子和分母部分均为整数， 便于计算。 计算得到Rλ后通过查表可以得到各目标的方位向相位信息， Z为查找表的深度。

对于各目标的的延迟， 等效为计算各散射点所处的距离门， 处理方法与计算Rλ时采用的方法类似， 其表达式为

式中： Z1=2m（m为整数）； ΔR=c/（2fs）， c为光速， fs为系统函数采样频率； Z1的作用与Z0相同。

3实验仿真步骤

本文采用基于等效散射体的回波模拟算法［18-19］作为信号处理的算法。

首先设置雷达参数， 根据已设置的参数生成LFM作为雷达发射信号， 再输入仿真场景参数， 以等距离环和方位向分辨单元对仿真场景进行网格划分， 对于t∈［0，T）， 使用多阶泰勒级数展开计算当前时刻雷达天线发射波束覆盖范围内所有等效散射点的距离历程， 并按编号R-1～R-m依次进行存储（软件上直接存为当前目录下的文件）， 然后根据式（8）计算覆盖范围内所有散射点的回波系统函数并叠加， 然后对雷达发射信号s（t）和回波系统函数进行卷积处理得到当前时刻的回波信号； 对于t≥T， 根据n=MOD（t/T）/PRI调用编号为n的距离历程数据， 之后的回波系统函数继续按式（8）计算， 然后通过卷积得到回波信号； 当t>N*T时仿真结束， 得到了整个场景的目标回波信号。 具体仿真流程， 如图4所示。

本文选用线性调频变标（Chirp Scaling， CS）算法作为成像算法。 如图5所示， 首先将仿真得到的场景回波数据在方位向做快速傅里叶变换（Fast Fourier Transform， FFT）， 并做变标处理， 使所有距离单元的距离徙动与参考距离处的距离徙动曲线相同， 然后距离向FFT， 进行一致距离徙动校正和距离匹配滤波， 经由距离向逆快速傅里叶变换（Inverse Fast Fourier Transform， IFFT）后进行残余相位补偿和方位匹配滤波， 最后经方位向IFFT完成方位压缩后可以得到最终成像结果。

4仿真实验与分析

4.1最优泰勒级数展开阶数仿真

以式（11）为例进行仿真， 仿真区域中心距离为20 km， 仿真中心所在平面与雷达平台呈45°俯仰角， 仿真中偏离中心点x0的距离范围为［-1 km，1 km］， 仿真选取的阶数为3～6项， 仿真结果如图6所示。

由图6可以看出， 偏离中心距离越远， 距离计算的误差越大， 根据仿真结果， 表1列出了不同阶数泰勒级数展开在偏离中心距离1 km处的距离计算误差。

根据所要求的相位误差， 可以求得距离计算误差的精度， 其表达式为

式中： ΔR为距离计算的误差； Δθ为所要求的相位误差； c为光速； fc为雷达载频。

根据后续仿真要求， 雷达载频为16 GHz， 相位误差为3°时要求距离精度为0.156 mm。 由表1可以看出， 如果偏离仿真中心的距离小于1 km时， 采用4阶、 5阶、 6阶泰勒级数展开进行仿真得到的距离计算误差非常小， 均小于0.1 mm， 可以满足仿真要求。

考虑到泰勒展开项数越多， 资源消耗越大， 4阶泰勒级数展开为最优泰勒级数展开阶数。 计算回波系统函数时， 使用4阶泰勒级数展开对距离历程进行计算。 其中， 1阶展开项负责对该目标点相对于基准点在距离向或方位向的直线距离进行计算； 2阶展开项反映了距离历程曲线的凹凸性， 当2阶系数不为0时， 该项是对1阶展开项产生的计算误差进行大幅度校正； 3阶、 4阶展开项都是对前项产生的距离计算误差进行小幅度校正。

4.2点目标回波模拟和成像

设参考距离R0=20 km， 对9个位置分布如表2所示的点目标进行回波模拟和成像。

仿真时设置的雷达参数如表3所示。

使用MATLAB軟件作为仿真工具， 分别使用开方和4阶泰勒级数展开对点目标的距离历程进行计算， 并用CS算法进行最终成像， 得到的成像结果， 如图7所示。

由图7可以看出， 使用两种方法生成的回波信号均具有良好的成像效果， 能有效分辨9个目标。

下面对位于场景中心的点目标1的性能参数进行分析， 包括冲击响应宽度（Impulse Response Width， IRW）、 峰值旁瓣比（Peak Sidelobe Ratio， PSLR）和积分旁瓣比（Integrated Sidelobe Ratio， ISLR）， 并与基于二维频域的快速算法的回波模拟算法进行比较。 距离向上各参数对比如表4所示， 方位向上各参数对比如表5所示。

由表4～5中数据可以看出， 使用3种仿真方法生成的点目标1的回波信号距离向和方位向的3种性能参数相差不多， 均与理论值相似， 只有基于二维频域的快速算法在IBW参数上与理论值存在偏差。 3种方法生成回波的用时如表6所示。

由表6可以看出， 使用4阶泰勒级数展开对距离历程计算可以使得生成回波信号的时间减少约53%， 虽然不及基于二维频域的快速算法快， 但也相差不大， 且二维频域快速算法存在局限性， 仅适用于正侧视及小斜视角情况， 而前面两种方法不存在此问题。

4.3真实场景回波模拟和成像

仿真设置的雷达参数如表3所示。 以自然场景的数据-RADARSAT-1的部分数据作为实验对象， 该场景大小为1 536（方位向）×2 048（距离向）， 原始图像如图8所示。

采用基于等效散射体的回波模拟算法对原始图像数据进行信号处理， 得到的回波信号如图9（a）所示， 对得到的回波信号进行CS算法重构， 重构后的回波信号如图9（b）所示。

对重构后的信号方位匹配滤波、 相位滤波后进行成像， 得到自然场景成像图， 如图10所示。

从成像结果可以看出， 文中算法所生成的回波信号经CS算法成像后具有良好的成像效果， 能将原始图像中的大多数细节展现出来， 表明该算法可以应用于大场景的回波模拟； 从过程来看， 该算法使用多阶泰勒级数展开和数据外推对距离历程进行计算， 使得回波系统函数的计算量大大减少， 在提高回波模拟实时性方面具有一定的意义。

5结论

本文提出使用多阶泰勒级数展开对距离历程的计算， 通过对比不同阶数泰勒级数展开所引起的计算误差大小， 根据仿真要求选取了误差精度达到0.085 mm且资源消耗最少的4阶泰勒级数展开。 从理论上分析了距离历程模型的规律性， 提出存储部分距离数据供后续时刻计算时调用， 进一步降低计算量。 通过对9个分布密集的点目标的回波模拟和成像， 验证了使用4阶泰勒级数展开计算距离历程对回波模拟实时性的提升， 最后通过仿真得到一幅SAR真实场景的回波信号， 并使用CS算法重构得到原场景， 证明了该方法的可行性。

参考文献：

［1］ 张洪欣，  张成亮. 基于复杂真实场景的合成孔径雷达原始回波数据的一种模拟方法［J］. 现代电子技术，  2001，  24（3）：  25-27.

Zhang Hongxin，  Zhang Chengliang. A Simulation Method of Raw Echo Data of Synthetic Aperture Radar Based on Complex Real Scene［J］. Modern Electronics Technique，  2001，  24（3）：  25-27.（in Chinese）

［2］ 周秀芝，  崔益鹏，  孙忠云. 雷达成像仿真研究综述［J］. 计算机与现代化，  2021（8）：  30-34.

Zhou Xiuzhi，  Cui Yipeng，  Sun Zhongyun. Overview of Radar Imaging Simulation Research［J］. Computer and Modernization，  2021（8）：  30-34.（in Chinese）

［3］ 李高源，  王晋宇，  张长弓，  等. SAR图像仿真方法研究综述［J］. 计算机工程与应用，  2021，  57（15）：  62-72.

Li Gaoyuan，  Wang Jinyu，  Zhang Changgong，  et al. Review of SAR Image Simulation Methods［J］. Computer Engineering and Applications，  2021，  57（15）：  62-72.（in Chinese）

［4］  Lin P，  Yu Z，  Li C S. A Generalized Method of Synthetic Aperture Radar Echo Simulation Based on the Theory of Electromagnetic Scattering［C］∥IEEE International Geoscience and Remote Sensing Symposium （IGARSS）， 2014：  1340-1343.

［5］  Luo Y H，  Song H J，  Wang R，  et al. An Accurate and Efficient Extended Scene Simulator for FMCW SAR with Static and Moving Targets［J］. IEEE Geoscience and Remote Sensing Letters，  2014，  11（10）：  1672-1676.

［6］  梁昕，  李海林. SAR目標回波模拟器的设计与实现［J］. 自动化技术与应用，  2020，  39（11）：  55-59.

Liang Xin，  Li Hailin. Design and Implementation of SAR Target Echo Simulator［J］. Techniques of Automation and Applications，  2020，  39（11）：  55-59.（in Chinese）

［7］ 易勇军，  宗竹林，  田忠. 一种基于FPGA的自然场景的实时SAR回波模拟器［J］. 现代雷达，  2013，  35（2）：  13-17.

Yi Yongjun，  Zong Zhulin，  Tian Zhong. A Real-Time SAR Echo Simulator for Natural Scene Based on FPGA［J］. Modern Radar，  2013，  35（2）：  13-17.（in Chinese）

［8］  Clemente C，  di Bisceglie M，  Di Santo M，  et al. Processing of Synthetic Aperture Radar Data with GPGPU［C］∥IEEE Workshop on Signal Processing Systems，  2009：  309-314.

［9］  王海華. 基于GPU的合成孔径雷达回波仿真技术研究［D］. 成都：  电子科技大学，  2009.

Wang Haihua. Research on Simulation Technology of Synthetic Aperture Radar Echo Based on GPU［D］.Chengdu：  University of Electronic Science and Technology of China，  2009. （in Chinese）

［10］  Xu Y H，  Zeng D Z，  Yan T，  et al. A Real-Time SAR Echo Simulator Based on FPGA and Parallel Computing［J］. TELKOMNIKA （Telecommunication Computing Electronics and Control），  2015，  13（3）：  806.

［11］  Shu T，  Tang B，  Yin K J，  et al. Development of Multichannel Real-Time Hardware-in-the-Loop Radar Environment Simulator for Missile-Borne Synthetic Aperture Radar［C］∥IEEE Radar Conference （RadarCon），  2015：  368-373.

［12］ 吴佳晔， 顾丹丹， 刘鹏.基于子孔径处理的大斜视SAR点目标仿真［J］.上海航天（中英文）， 2021， 38（05）： 120-130.

Wu Jiaye，  Gu Dandan，  Liu Peng. Point Target Simulation of Large Squint SAR Based on Subaperture Processing［J］. Aerospace Shanghai （Chinese & English）， 2021，  38（5）：  120-130.

［13］ 刘彦斌，  孙光才，  邢孟道，  等. 基于子孔径数据流的星载SAR实时成像算法研究［C］∥第六届高分辨率对地观测学术年会论文集（下）， 2019：  204-214.

Liu Yanbin，  Sun Guangcai，Xing Mengdao，et al. Research on Real-Time Imaging Algorithm for Spaceborne SAR Based on Sub Aperture Data Streams［C］∥6th Annual High Resolution Earth Observation Academic Conference （Part 2），  2019：  204-214.（in Chinese）

［14］ 叶铮，  朱岱寅，  吴迪. 一种基于重叠子孔径回波信息的SAR图像配准算法［J/OL］. 航空学报，  2022： 1-12.

Ye Zheng，  Zhu Daiyin，  Wu Di. SAR Image Registration Algorithm Based on Echo Information of Overlapping Subaperture［J/OL］. Acta Aeronautica et Astronautica Sinica，  2022： 1-12.（in Chinese）

［15］  戴长俊. 合成孔径雷达高效回波与干扰模拟方法［D］. 成都：  电子科技大学，  2022.

Dai Changjun. Simulation Method of High-Efficiency Echo and Interference of Synthetic Aperture Radar［D］.Chengdu：  University of Electronic Science and Technology of China，  2022. （in Chinese）

［16］  Zhang S，  Hou X，  Hu X C，  et al. Stitching Interferometry Using Computer-Generated Hologram （CGH） Based on Sub-Aperture Adjustment Aberration of 2-D Chebyshev Polynomial［J］. Optics and Lasers in Engineering，  2021，  143：  106618.

［17］  Li N，  Sun G C，  Li B Y，  et al. High Squint Multichannel SAR Imaging Algorithm for High Speed Maneuvering Platforms with Small-Aperture［J］. Signal Processing，  2021，  185：  108078.

［18］  Xie H T，  An D X，  Huang X T，  et al. Efficient Raw Signal Generation Based on Equivalent Scatterer and Subaperture Processing for One-Stationary Bistatic SAR Including Motion Errors［J］. IEEE Transactions on Geoscience and Remote Sensing，  2016，  54（6）：  3360-3377.

［19］  Lu Y，  Zhang S S，  Cao J S. A Raw Echo Simulation Algorithm Based on Equivalent Scatterer for Bistatic SAR［C］∥International Workshop on Microwave and Millimeter Wave Circuits and System Technology，  2012：  1-4.

A Fast RealTime Calculation Method for SAR Echo History

Xing Chen， Pan Minghai*

（College of Electronic and Information Engineering ， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China）

Abstract：

Aiming at the problem that the simulation calculation of synthetic aperture radar （SAR） target echo is too large， two multiorder Taylor series expansions are used to calculate the distance history in the echo system function， and the fast realtime calculation of the distance history is completed by combining the data extrapolation method. This method uses multiple multiplications and additions instead of square root operation with large amount of calculation， which can ensure the realtime performance of distance calculation under the premise of certain calculation accuracy. At the same time， combined with the regularity of distance history model， data extrapolation is used instead of repeated calculation process to further reduce the amount of calculation and improve realtime performance. By comparing the calculation error of different orders of Taylor series expansion at the same distance， the fourth order is the optimal Taylor expansion order under this simulation condition. Finally， the echo simulation and imaging of 9 densely distributed point targets and real scene targets are carried out respectively. The point target simulation results show that the method can reduce the time of generating echo signal by 53 % and increase the speed by 2 times without affecting the performance of echo signal. The real scene simulation results show that the method can be applied to the echo simulation of large scenes.

Key words： echo simulation； echo system function； realtime calculation； distance history；  data extrapolation; point target; SAR