一种高精度星敏感器抗地气光星图预处理算法

刘宇鑫 王新龙 胡晓东 王勋

摘要：      近地空间飞行器所搭载的星敏感器易受地气光影响， 导致星点提取精度较低进而影响天文导航的精度。 针对这一问题， 本文提出了一种高精度的抗地气光星图预处理算法。 通过分析地气光的传播机理， 建立地球大气散射以及地表反射模型， 构建了一种精确的地气光辐射强度模型。 通过分析星敏感器像面上局部范围内所接收地气光的传输路径与像素坐标之间的关系， 对辐射强度模型进行变换得到了局部邻域内的地气光背景灰度模型， 进而利用背景估计法实现对地气光影响下的杂散光背景的精确估计与补偿。 最后， 通过仿真以及实拍星图对算法性能进行验证， 结果表明所设计算法能有效提升星图信噪比以及质心提取精度， 并且具有较好的抗干扰能力。

关键词：     星敏感器； 地气光； 大气散射； 背景估计； 星图预处理; 导航

中图分类号：     TJ760; V448    文章编号：     1673-5048（2023）04-0091-07

文献标识码：    A    DOI： 10.12132/ISSN.1673-5048.2022.0224

0引言

星敏感器是一种以恒星作为观测对象的天体敏感器， 具有自主性好、 测量精度高、 无累积误差、 体积和质量小等优势［1］， 在航空航天飞行器上有广泛应用。 星敏感器工作时， 除了接收到目标恒星的辐射能量外， 还会受到太阳光、 月光、 地气光、 地球热等杂散辐射的影响［2］。 其中， 地气光是太阳光经复杂的大气散射及地表反射后形成的［3］， 会在星敏感器像平面上形成非均匀背景灰度， 进而降低像平面的对比度以及恒星的信噪比， 影响星点质心的提取精度及天文导航精度。 因此， 对于近地空间飞行器所搭载的星敏感器而言， 如何消除地气光对星图的影响是天文导航亟待解决的一项关键技术。

目前消除地气光对星图影响的方法有三类： 频域特征消除法、 空间域特征消除法和背景估计消除法。 频域特征消除法是利用星点在频域中呈现的高频特性， 与低频的背景进行区分， 进而去除地气光导致的背景灰度［4-5］。 但由于星图中地气光背景的频谱范围广， 星点与地气光背景在频域上存在混叠［6］， 使得该方法对地气光去除的效果不佳； 由于星点在空间域上表现出“凸起”的特点， 而地气光背景在空间域上变化较为平缓， 因此， 空间域特征消除法是利用星点与地气光背景在空间域上的差异， 使用形态学滤波或灰度前向差分等算法去除地气光背景［7-9］。 但对于地气光影响下的低信噪比星图而言， 星点通常被背景淹没导致其形态特点不显著， 该方法会将星点的部分区域视为背景予以去除， 进而破坏星点的能量分布， 影响质心提取精度； 背景估计消除法是基于局部区域内地气光背景灰度值的相关性， 将背景灰度建模成一个平面， 再利用相邻像素的灰度值对星点处的背景灰度进行估计与补偿［10-12］， 进而消除地气光对星图的影响。 由于星点成像的几何位置集中， 在背景估计时可以通过设计模板对星点进行规避［10，  13］， 使得该算法对星点能像分布的破坏程度较小， 具有较好的预处理效果。 但实际的地气光是经复杂的散射以及反射后形成的， 其在像平面上的分布规律复杂多变， 难以使用平面背景模型对其进行精确描述， 导致对地气光背景的估计精度不佳， 制约了其对地气光背景的去除效果。

本文通过分析太阳光经过地球-大气系统的散射以 及反射，  構建了一种精确的地气光辐射强度模型， 并分析地气光背景灰度在星图中的分布规律， 进而设计了一种基于三次曲面模型的抗地气光星图预处理算法。

1地气光辐射强度模型

地气光会在星敏感器像平面上形成非均匀的背景灰度， 影响星点质心的提取精度及天文导航精度。 为定量分析其在星敏感器像平面上的分布规律， 需建立地气光的辐射强度模型，  以分析像平面上各像素所接收到的地气光辐射强度。

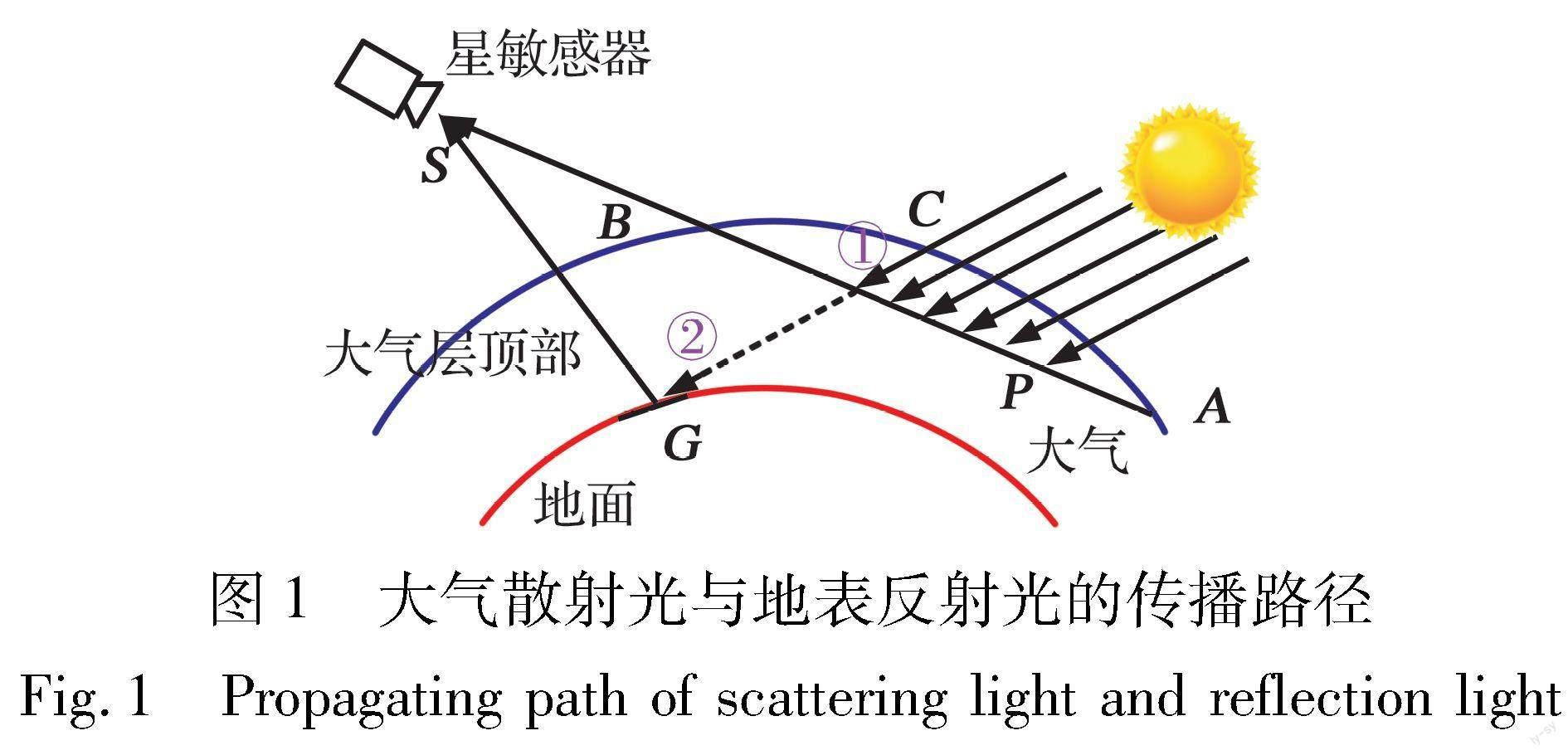
太阳光经过地球大气散射与地表反射作用后形成地气光。 实际上，  由于大气密度随高度和大气层温度变化较大， 受非均匀大气的折射作用， 光线沿曲线传播， 但大气折射所导致的光线偏折角小于38′， 对光线的辐射强度影响及其分布规律影响不大。 因此， 为简化分析过程， 对光线到达星敏感器入瞳平面的路径采用了直线假设， 其传播路径如图1所示。

图中， 路径①为大气散射光的传播路径， 太阳光从大气C处射入， 在大气中P发生散射， 再从A点穿出大气层到达星敏感器入瞳平面S。 路径②为地表反射光的传播路径， 太阳光经大气C处射入， 穿过大气到达地球表面G， 在地表反射后穿出大气层达到星敏感器入瞳平面S。

大气散射光与地表散射光叠加后形成地气光。 为建立地气光的辐射强度模型， 可先分别建立大气散射光与地表散射光的辐射强度模型。

1.1大气散射光辐射强度模型

为建立大气散射光的辐射强度模型， 以一束大气散射光线为例， 其在大气中的传播路径如图2所示。

太阳光从C点射入大气， 在P点以散射角θ发生散射， 散射后光线从A点射出大气。

光线在大气中传输， 受大气的吸收和散射作用后发生衰减， 根据朗伯-比尔定律［13］ ， 可计算得到P点的光线辐射强度为

IP=IsT（CP）（1）

式中： Is为大气表面的太阳光辐射强度； T（CP）是衰减系数， 表示光线在CP路径上传输过程中的衰减程度， 可表示为

式中： β（λ）为散射系数； D（CP）为路径CP的光学距离； ρ（h）为不同高度处的大气密度； s为光线传输路径长度。

光线在P点发生散射， 散射光沿路径PA传播， 经大气影响衰减后从A点射出大气， 其辐射强度为

IPA=IPS（λ，  θ，  h）T（PA）（4）

式中： S为散射方程，  S=β（λ）ρ（h）γ（θ）， γ（θ）为散射的相位函数； T（PA）为光线在路径PA上的衰减系数。

在实际过程中， 太阳光在路径AB上各点都发生了散射， 因此将式（4）的单束散射光在A点的辐射强度沿散射路径AB积分， 可得A点射出的大气散射光辐射强度表示为

式中： l为散射路径长度。

根据A点的大气散射光辐射强度， 可计算得到以不同散射角散射的光线辐射强度。

1.2地表反射光辐射强度模型

太阳照射在地球表面形成阳照区， 阳照区内的地表面元向外反射太阳光， 穿出大气后形成地表反射光。 取地表G点处的面元i进行分析， 在该面元处发生反射的光路如图3所示。

式中： d为日地距离； BRDFi为该地表面元沿着目标方向的双向反射分布函数， 可由参数化的BRDF模型计算得到［15］； 面元i的面积为dAi； θr为反射光与法线的夹角。

反射光线受大气影响衰减后从A点射出大气， 其辐射强度为

exp{－β（λ）［D（CG）+D（GA）］}dAi（9）

综合考虑大气散射效应及地表反射效应， 对式（5）的大气散射光辐射度与式（9）的地表反射光辐射强度求和， 得到从A点处射出大气的地气光辐射强度模型：

IA=IA， s+IA， r（10）

基于式（10）的地气光辐射强度模型， 可探究影响地气光辐射强度的因素， 进而分析地气光背景在星敏感器像平面上的分布规律。

2地气光辐射强度特性分析

地气光由地表反射光与大气散射光共同构成， 但由于地球对导航星的遮挡作用， 地表反射光所影响的星图区域内不存在星像点， 因此地表反射光不会影响星点的成像。 星图中星像点的背景灰度主要由大气散射光所导致， 它是影响星点成像的主要因素， 需对其辐射强度特性进行分析。

如式（5）所示， 大气散射光的辐射强度模型描述为

由于大气的厚度远小于地球半径， 且大气层的曲率较小， 太阳光入射路径CP的长度远小于出射路径PA的长度。 此外， 太阳光入射所处的高度较高， 大气稀薄， 因此， 光线传输过程的光学距离D（CP）远小于D（PA）。 为简化分析过程， 可忽略D（CP）项， 将式（11）简化为

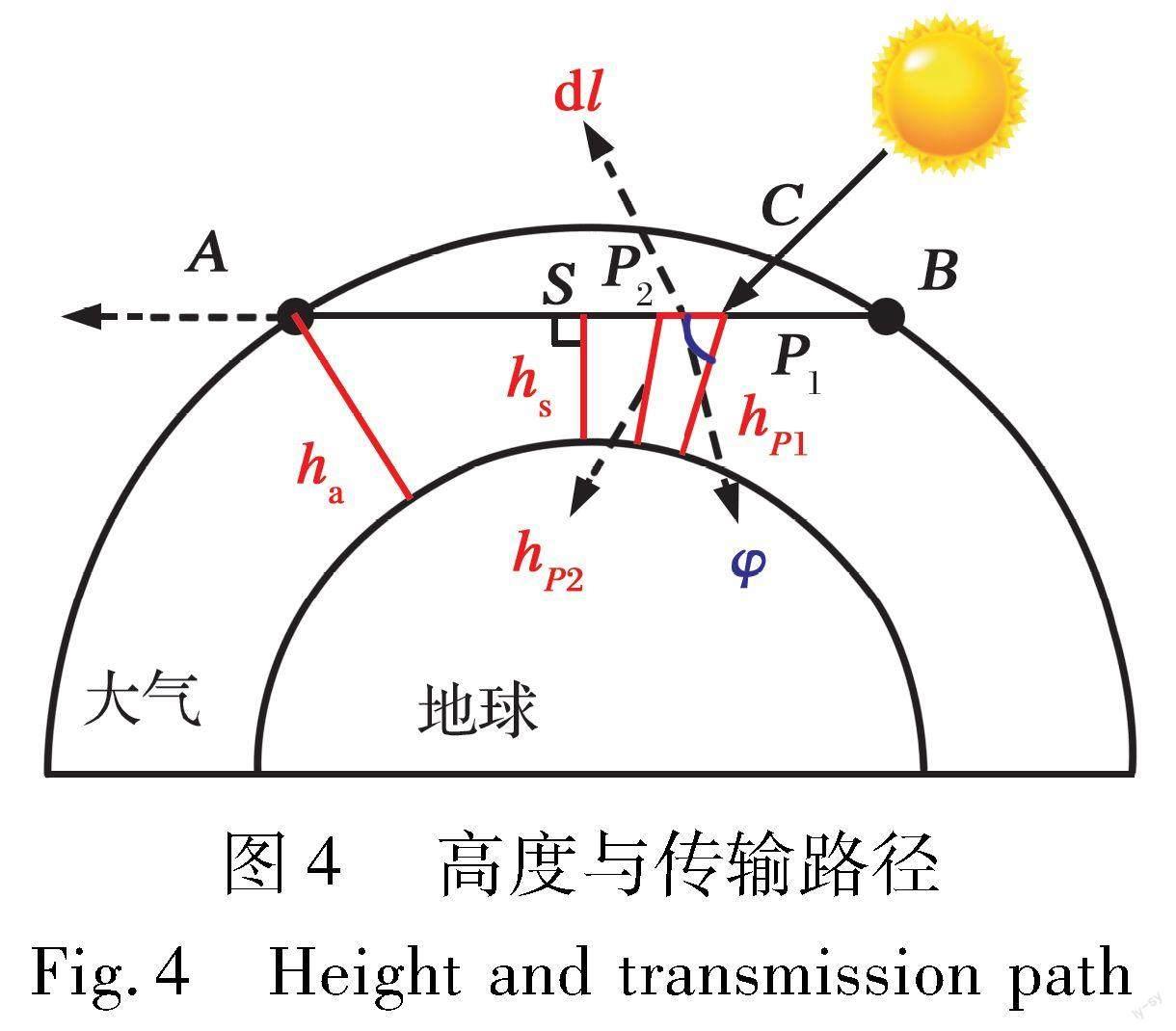
如图4所示， 根据几何关系， 可得散射路径长度的微分dl与散射点高度的微分dh间的关系：

dl=k（hP1－hP2）=kdh （13）

式中： k=secφ， φ为散射路径方向矢量与散射点的位置矢量之间夹角的补角。

由于光线传输路径长度远小于地球半径， 散射路径上各点所对应的φ变化幅度较小， 不超过5°， 可视为常值。 对式（13）积分， 可得散射路径长度l与高度h间的关系， 即

式中： hs为散射路径的高度。

大气密度ρ与高度h近似成指数关系［16］， 即

式中： ρ0为高度h0处的大气密度； H为密度标尺高度。

将式（13）～（15）代入D（PA）， 则

将式（16）代入式（12）中， 并将积分变量散射路径长度l替换为散射高度h可得

由上式可知， 大气散射光的辐射强度可表示为光线波长λ、 散射角度θ以及散射高度hs的函数。

將地球和大气视为理想的球体， 则根据几何关系， 可得散射高度hs和散射路径长度l间的关系， 即

式中： Re为地球半径； datm为地球大气厚度。

由此可将大气散射光辐射强度模型中的f（hs）表示为散射路径长度l的函数f（l）。

对星敏感器而言， 其所能敏感的光线波长固定， 即β（λ）为常数。 令传输系数T（l）=β（λ）f（l）， 则可将大气散射光辐射强度模型改写为

IA， s=Isγ（θ）T（l） （19）

式（19）表示了大气散射光的辐射强度IA， s和日光辐射强度Is、 散射角θ以及散射路径长度l的关系。 由于日光辐射强度为常数， 可知大气散射光的辐射强度仅与散射角以及散射路径长度相关， 即影响星点成像的地气光的辐射强度受散射角和散射路径长度的影响。

3基于地气光背景灰度模型的预处理算法

基于以上对地气光辐射强度特性的分析， 探究了地气光背景在星图中的分布规律， 进而构建了局部区域内的地气光背景灰度模型， 然后基于该模型设计了一种抗地气光的星图预处理算法， 如图5所示。

利用星图中某点的相邻像素的灰度值， 对局部范围内背景灰度模型的相关参数进行估计， 进而计算得到该点的背景灰度值。 再从原始星图中减去该灰度值， 以实现地气光背景的补偿， 得到预处理后星图。

3.1局部范围的背景灰度模型

天文导航中使用的导航星光高度通常高于20 km［16］， 相对应区域内大气散射光的散射路径长度l与传输系数T（l）的关系如图6所示。

在背景估计过程中， 取像素邻域的范围为10 pixel×10 pixel。 对于近地空间飞行器而言， 其飞行高度通常低于200 km， 在局部像素邻域范围内所接收到的地气光在大气中的散射路径长度变化幅度不超过300 km， 因此， 可用三次函数对图6中的传输系数进行分段拟合， 即

T（l）=k1l3+k2l2+k3l+k4（20）

式中： ki（i=1，  2，  3，  4）为模型系数。

此外， 由几何关系可知， 在局部像素邻域范围内， 所接收到的地气光在大气中的散射路径长度连续单调变化， 如图7所示。 由于其变化幅度远小于散射路径长度， 因此可认为该散射路径沿长度星图的x方向与y方向线性变化， 利用斜面模型近似描述局部区域内光线在大气中的散射路径长度， 即

l（x， y）=k5x+k6y+k7（21）

式中： ki（i=5， 6， 7）为模型系数。

将式（20）～（21）代入式（19）的大气散射辐射强度模型中， 可得到局部像素范围内的地气光辐射强度模型：

IA， s=Isγ（θ）T（λ， l）=Isγ（θ）（ax3+bx2y+cx2+dxy2+exy+fx+gy3+hy2+iy+j） （22）

式中： a， b， c， d， e， f， g， h， i， j为模型的系数， 在局部像素范围内为常值。

大气中发生的散射以瑞利散射与米氏散射为主［17］， 其散射相位方程为

式中： k为对称系数。

对式（23）和式（24）两侧同时微分， 可得

在局部像素邻域范围内， 散射角度的变化幅度不超过0.2°， 散射系数γ（θ）的变化幅度不超过6.5×10-4， 其变化率低于0.035%， 远小于传输系数的变化率， 因此在局部像素邻域范围内， 可将散射系数γ（θ）视为常值。

由此可将式（22）的地气光辐射强度模型改写为

IA， s=c2（ax3+bx2y+cx2+dxy2+exy+fx+

gy3+hy2+iy+j） （27）

式中： c2为常数， c2=Isγ（θ）。

式（27）即为局部范围内的地气光辐射强度模型， 其光线辐射强度为像素坐标的函数。

根据星敏感器入射光强与像素成像灰度间的线性关系， 可建立局部范围内的背景灰度模型：

G（x， y）=KIA， s（x， y）+G0=aKc2x3+bKc2x2y+cKc2x2+dKc2xy2+eKc2xy+fKc2x+gKc2y3+

hKc2y2+iKc2y+jKc2+G0 （28）

式中： G（x， y）为像素的灰度值； K为常值比例系数，

由星敏感器硬件参数决定； G0为初始背景灰度值。

由式（28）可知， 局部区域内的地气光背景灰度沿三次曲面分布。

3.2模型参数估计

为减小随机成像噪声对地气光背景估计产生干扰， 使用最小二乘法利用星点周围像素的灰度对地气光背景灰度模型的参数进行估计。

利用最小二乘法， 使残差平方和取极小值， 令残差平方和对各参数的导数为0， 可得方程组

AX^=Y（29）

求解此线性方程组得到高斯函数的各项参数：

X^=A－1Y（30）

式中： X^为式（28）中各参数的估计值； 矩阵A中各元素可根据滤波模板大小离线计算得到； 矩阵Y中各元素可通过对局部区域内的图像进行滤波得到。

因此， 使用本文算法进行预处理时， 只需构建相应的滤波模板， 通过图像的滤波处理来估计未知参数， 最终根据拟合参数求解中心像素的背景估计值， 则可得到星点处的地气光背景。 然后， 再从去噪后星图中减去背景估计值， 即可获得预处理后的星图。

4实验结果与分析

4.1仿真星图验证

4.1.1地气光影响下星图的仿真

以飞行高度为150 km的低轨飞行器为例， 设定其在惯性坐标系下的位置矢量rs=［0，  6 528.14，  0］（km）； 日光方向矢量rsun=［0，  0.493，  0.871］；  星敏感器的视轴指向地球边缘， 其方向矢量为raxis=［0.337，  -0.171，  0.926］。 星敏感器视场为12°×12°， 分辨率为1 024×1 024， 像元尺寸为0.012 mm。 采用SAO J2000星表中星等小于6 Mv的星构成用于生成模拟星图的星表。 仿真得到的地气光影响下的星图如图8所示。

图中的红框为星点位置， 紫色的横线为地球边缘在星图中的位置， 星图底部的星光被地球遮挡。

通过分析图像可知， 地气光在像平面上形成灰度连续渐变分布的背景， 覆盖了从地面到距离地表约60 km高度的区域。 其造成的背景灰度分布不均， 且随着离地距离的增加先增加后减小， 难以用简单的平面描述。 若直接对该星图进行阈值分割与质心提取， 则星图下部区域的低信噪比星点容易发生漏检， 而上部将出现大量的虚警， 难以精确地完成质心提取任务。

4.1.2仿真星图預处理

利用本文算法对星图进行预处理， 得到的结果如图9所示。

通过分析预处理后的星图可知， 本文算法能有效去除地气光所造成的背景灰度。

为验证算法的性能， 选用基于平面模型的最大背景估计法［10］， 基于改进Top-Hat变换的形态学滤波法［7］， 与本文算法对星图进行预处理。 以星图中最左侧受地气光影响较为严重的星点为例进行分析， 标准星图、 地气光影响下的星图与预处理后局部星图如图10所示。

通过对比标准星图与预处理后的局部星图可知， 最大背景估计法预处理后能保持星点的灰度分布特征， 但由于该算法将杂光背景灰度建模为等值面， 与实际的地气光分布规律不符， 导致该算法仅能对地气光背景中分布较为均匀的部分进行估计与补偿， 对地气光背景的去除效果不佳； 基于改进Top-Hat变换的形态学滤波法能有效去除星图中的背景， 但由于地气光影响下星点被淹没在背景中， 与背景间的形态学关系不明显， 该算法将星像点的边缘部分视为背景灰度予以去除， 严重破坏了星点灰度分布特征； 本文算法通过设计滤波模板对星点进行规避， 可有效保护星点的灰度分布特征。 此外， 本文算法采用了较为精准的背景模型， 符合背景灰度的变化规律， 因此能有效去除地气光造成的非均匀背景灰度。

为进一步分析各算法性能， 将星图预处理前后的背景平均灰度、 单星信噪比、 信噪比提升倍数以及质心提取精度进行对比， 如表1所示。

从表1可以看出， 最大背景估计法预处理后的星图中背景灰度较高， 对地气光背景的去除不充分， 星图中残余的地气光背景灰度会影响质心提取精度， 导致其提取精度低； 形态学滤波法预处理后星图信噪比较低， 并且破坏了星点的灰度分布特征， 进而导致其质心提取成功率以及提取精度低； 本文算法能在保留星点特征的前提下精确地去除非均匀背景灰度， 显著提升了星图信噪比， 并且相比于最大背景估计法能提高约40%的质心提取精度， 具有较好的预处理效果。

4.2实拍星图验证

进一步开展地气光影响下的观星实验， 得到了地气光影响下的实拍星图。  利用基于平面模型的最大背景估计法、 基于改进Top-Hat变换的形态学滤波法， 与本文算法对星图进行预处理， 以其中一幅典型星图为例进行对比， 如图11所示。

如图11（a）所示， 实拍星图中除了地气光所导致的背景灰度外， 还可能受到云层、 空间碎片等其他干扰源的影响， 在星图中形成局部高亮区域。 在局部高亮区域内， 背景灰度的变化剧烈， 难以用简单的平面模型描述其变化规律， 因此， 基于平面模型的最大背景估计法对实拍星图中的背景灰度去除效果不佳， 保留了背景中的高亮部分， 进而造成误识别的现象； 形态学滤波法严重破坏了星点的能量分布， 因而对星点的提取失败； 本文设计算法基于三次曲面模型对星图背景进行估计， 对于背景灰度变化剧烈的高亮区域， 所建立的三次曲面模型仍能较为精准地反映背景灰度在局部区域内的分布规律， 进而通过对曲面模型参数进行拟合， 可对背景灰度进行有效的估计与补偿， 解决了将杂散光背景误识别为星点的问题， 具有较强的抗干扰能力， 适用范围较广。

利用以上三种算法对20张实拍星图进行预处理， 统计所得的星点检测率、 星点误检率以及信噪比提升倍数如表2所示。

通过分析预处理结果可知， 本文算法能更有效地提高星图的信噪比， 进而提升星点检测率。 此外， 该算法对复杂背景也有较好的去除效果， 减少了背景所造成的伪星， 降低星点误检率， 具有较强的抗干扰能力。

5结论

为消除地气光对星图的影响， 本文提出了一种基于地气光背景灰度模型的星图预处理算法。 通过分析地气光的传播机理， 构建了一种精确的地气光辐射强度模型， 并揭示了地气光的辐射强度与散射角和散射路径长度之间的关系。 基于此， 构建局部范围的地气光背景灰度模型用于地气光背景的估计与补偿。 本文算法采用的背景灰度模型能精确地反映地气光背景的复杂分布规律， 通过拟合模型中的参数， 可实现对分布复杂的杂散光背景的精确估计与补偿。 此外， 对于其他干扰源所造成的杂散光， 所建立的背景模型在局部区域内仍能较精确地描述其变化规律， 能对其进行精确的估计与补偿， 具有较强的抗干扰能力， 可有效消除地气光对星图的影响， 保证了地气光干扰下的星像点质心定位精度。

参考文献：

［1］ 杨阳，  王宏力，  陆敬辉，  等. 地气光对星敏感器星提取精度影响分析［J］. 光电工程，  2016，  43（4）： 8-14.

Yang Yang，  Wang Hongli，  Lu Jinghui，  et al. Analysis of Impact of Earth and Atmosphere Radiation on Star Extraction Accuracy of the Star Sensor［J］. OptoElectronic Engineering，  2016，  43（4）： 8-14.（in Chinese）

［2］ 杜伟峰，  王燕清，  郑循江，  等. 星敏感器杂散光抑制设计与验证［J/OL］. 光学学报，  2022： 1-10.

Du Weifeng，  Wang Yanqing，  Zheng Xunjiang，  et al. Design and Verification of Stray Light Suppression for Star Sensor［J/OL］. Acta Optica Sinica，  2022： 1-10.（in Chinese）

［3］ Nayar S K，  Narasimhan S G. Vision in Bad Weather［C］∥Proceedings of the Seventh IEEE International Conference on Computer Vision，  2002： 820-827.

［4］ Wen J T . A New Binarization Method for NonUniform Illuminated Document Images［J］. Pattern Recognition，  2013，  46（6）： 1670-1690.

［5］ Liu N，  Xie J. Interframe PhaseCorrelated Registration SceneBased Nonuniformity Correction Technology［J］. Infrared Physics & Technology，  2015，  69： 198-205.

［6］ 毛曉楠，  梁为升，  郑循江. 基于并行运算体系结构的星敏感器图像处理算法［J］. 宇航学报，  2011，  32（3）： 613-619.

Mao Xiaonan，  Liang Weisheng，  Zheng Xunjiang. A Parallel Computing Architecture Based Image Processing Algorithm for Star Sensor［J］. Journal of Astronautics，  2011，  32（3）： 613-619.（in Chinese）

［7］ Xu Z M，  Liu D，  Yan C X，  et al. Stray Light Nonuniform Background Correction for a WideField Surveillance System［J］. Applied Optics，  2020，  59（34）： 10719-10728.

［8］ Wang J N，  Wang X D，  Li Y H. Stray Light Nonuniform Background Elimination Method Based on Image Block SelfAdaptive GrayScale Morphology for WideField Surveillance［J］. Applied Sciences，  2022，  12（14）： 7299.

［9］ He Y Y，  Wang H L，  Feng L，  et al. A Novel Method of Eliminating Stray Light Interference for Star Sensor［J］. IEEE Sensors Journal，  2020，  20（15）： 8586-8596.

［10］ 余路伟，  毛晓楠，  周琦，  等. 采用最大背景估计的星敏感器图像处理方法［J］. 激光与红外，  2017，  47（7）： 889-895.

Yu Luwei，  Mao Xiaonan，  Zhou Qi，  et al. Image Processing of Star Sensor Based on Maximum Background Estimation［J］. Laser & Infrared，  2017，  47（7）： 889-895.（in Chinese）

［11］ Xu Q，  Zhao C H，  Qiao C，  et al. Star Centroid Extraction in Stray Light Background for Star Sensor［C］∥ International Conference on Signal Image Processing and Communication，  2021，  11848： 19-29.

［12］ 萬晓伟，  王刚毅，  魏新国，  等. 基于最优背景估计的星敏感器抗杂散光星点提取方法［J］. 红外与激光工程，  2022，  51（8）： 3788.

Wan Xiaowei，  Wang Gangyi，  Wei Xinguo，  et al. Star Spot Extraction Based on Optimal Background Estimation for Star Sensor Anti Stray Light［J］. Infrared and Laser Engineering，  2022，  51（8）： 3788.（in Chinese）

［13］ Cao Z，  Wang G Y，  Wei X G. Improving Star Centroiding Accuracy in Stray Light Base on Background Estimation［C］∥ IEEE 9th Annual Information Technology，  Electronics and Mobile Communication Conference （IEMCON），  2019： 513-518.

［14］ 张利强，  苏康，  郑昌文，  等. 地球与大气反射光对空间光学传感器探测能力的影响仿真研究［J］. 宇航学报，  2011，  32（2）： 233-241.

Zhang Liqiang，  Su Kang，  Zheng Changwen，  et al. Research on Simulation for Influence of Earth and Atmosphere Reflected Light on Detect Ability of Space Optical Sensor［J］. Journal of Astronautics，  2011，  32（2）： 233-241.（in Chinese）

［15］ Maignan F，  Breon F M，  Lacaze R. Bidirectional Reflectance of Earth Targets： Evaluation of Analytical Models Using a Large Set of Spaceborne Measurements with Emphasis on the Hot Spot［J］. Remote Sensing of Environment，  2004，  90（2）： 210-220.

［16］ 詹先軍，  王新龙，  胡晓东，  等. 大气层内载体星光折射间接敏感地平定位可行性分析［J］. 航空兵器，  2022，  29（1）： 107-112.

Zhan Xianjun，  Wang Xinlong，  Hu Xiaodong，  et al. Feasibility Analysis of Stellar Refraction Indirect Horizon Sensing Positioning on the Carrier Inside the Atmosphere［J］. Aero Weaponry，  2022，  29（1）： 107-112.（in Chinese）

［17］ Bruneton E，  Neyret F. Precomputed Atmospheric Scattering［J］. Computer Graphics Forum，  2008，  27（4）： 1079-1086.

A High Precision Star Image PreProcessing Method Against EarthAtmosphere Radiation of Star Sensor

Liu Yuxin1，  Wang Xinlong1*，  Hu Xiaodong2，  Wang Xun3

（1. School of Astronautics， Beihang University， Beijing 100083， China;

2. AVIC Xian Flight Automatic Control Research Institute， Xian 710065， China;

3. Beijing Institute of Automatic Control Equipment， Beijing 100074，  China）

Abstract： Star sensors installed on nearspace vehicles are susceptible to earthatmosphere radiation. As a result，  the accuracy of star extraction and the performance of celestial system is significantly degraded. Aiming at this problem，  a high precision star image preprocessing method to eliminate earthatmosphere radiation is proposed. By analyzing the propagation mechanism of earthatmosphere radiation，  the atmospheric scattering model and ground reflection model are established，  and an accurate earthatmosphere radiation intensity model is constructed. Subsequently，  the radiation intensity model is transformed into the background grayscale model in local ranges with the analysis of the relationship between the transmission path of the earthatmosphere radiation received in the local ranges of the star sensor image plane and the pixel coordinates. Furthermore，  the background estimation method is used to accurately estimate and compensate the stray light background under the influence of the earthatmosphere radiation. Eventually，  the performance of the proposed method is verified by simulated and real star images. The results show that the proposed method can effectively improve the SNR of star images and the accuracy of star extraction， and has good antiinterference performance.

Key words：star sensor; earthatmosphere radiation; atmospheric scattering; background estimation; star image preprocessing; navigation