BRIFT： 一种基于二值描述符的多模态图像匹配方法

许凯凯 郭鹏程 王晶晶

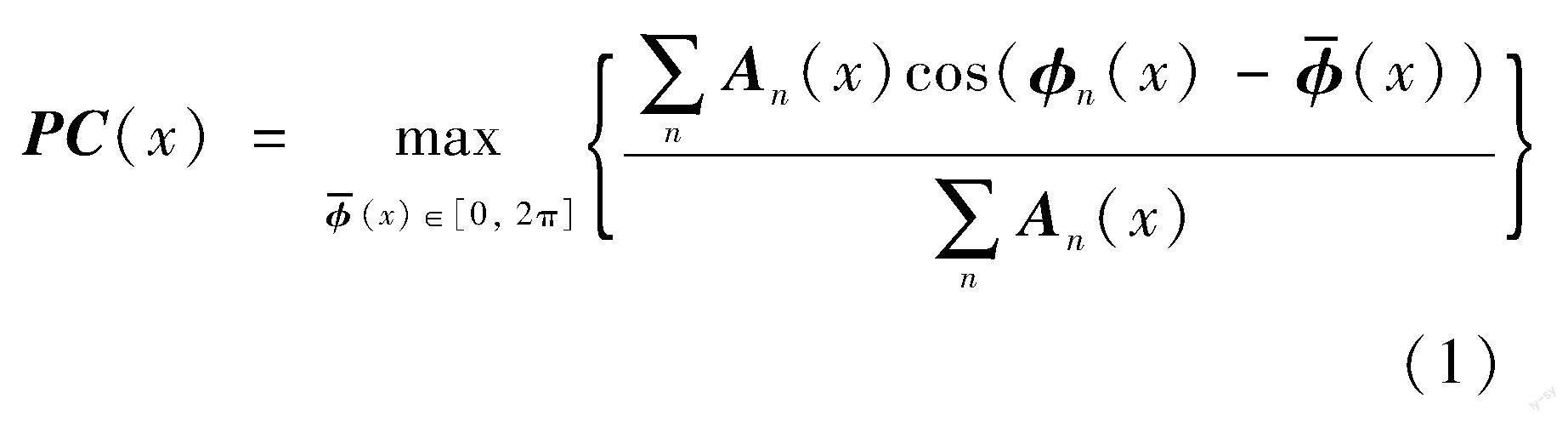
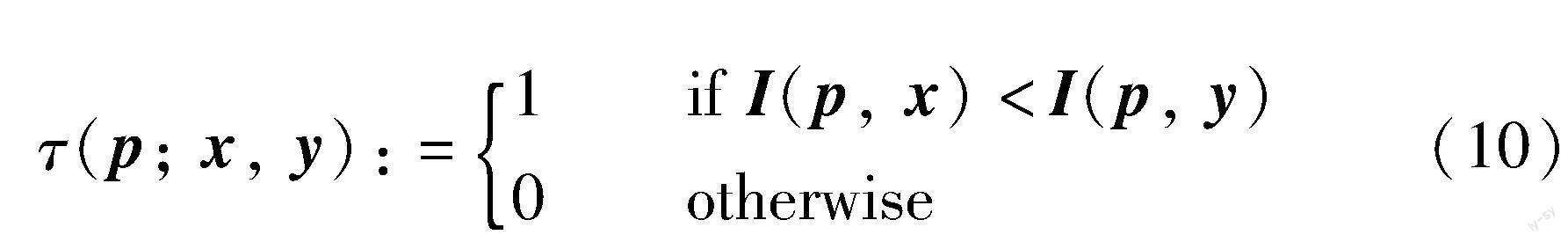
摘要：       针对使用辐射变化不敏感特征變换（RIFT）在最大索引图（MIM）上计算特征描述符、 进行特征匹配耗费时间长的问题， 提出了基于RIFT的二值描述符算法（BRIFT）。 首先计算图像的相位一致性并得到MIM， 然后在MIM上通过快速算法计算特征描述符并将其二值化， 最后利用Hamming距离作为距离测度进行匹配。 将存在多种几何畸变和辐射度变化的异源遥感图像作为测试数据， 将BRIFT算法分别与SIFT， BRISK， BRIEF， RIFT等方法进行对比， 结果表明， 在略微损失匹配精度的情况下， 所提BRIFT算法能节省约80%～90%的特征描述符计算时间， 节省约50%的特征匹配时间， 实现异源遥感图像的快速鲁棒匹配。

关键词：      图像匹配；  特征匹配；  相位一致性；  最大索引图；  二值描述符

中图分类号：       TJ760；  TP751    文章编号：      1673-5048（2023）04-0115-08

文献标识码：     A    DOI：  10.12132/ISSN.1673-5048.2022.0263

0引言

图像匹配是将由不同传感器、 在不同时间拍摄的图像在空间位置上进行对齐配准的过程。 由于不同传感器成像机理不同， 成像时间、 视角也不同， 因此图像配准可以提供互补的信息， 被广泛应用于如地物勘测、 图像融合、 图像检索、 变化检测、 计算机视觉等方面。 近年来， 随着红外、 激光、 SAR等成像技术的快速发展， 产生的海量数据对图像的快速鲁棒配准提出了更高要求。 此外， 由于异源图像通常由不同传感器在不同时间获得， 因此图像之间存在较大的非线性辐射度差异及时相差异， 导致图像匹配性能较差。

图像匹配方法通常分为三类： 基于灰度的图像匹配方法、 基于特征的图像匹配方法和基于表示的图像匹配方法。 基于灰度的图像匹配方法直接利用图像的灰度值， 即根据一定的相似性度量方法， 计算模板窗内两幅图像灰度值的相似度， 从而将相似度最大的位置作为匹配位置。 常用的相似性度量方法有平方差（Sum of Squared Difference，  SSD）［1］、 互相关（Cross Correlation，  CC）、 归一化互相关（Normalized Cross Correlation，  NCC）［2］和互信息（Mutual Information，  MI）［3］。 这类方法通常无法用来匹配含有非线性辐射度变化的多模态图像。 基于表示的图像匹配方法［4］首先利用机器学习等方法获得对待匹配区域的解释表示， 然后借助语义网络等方法， 实现图像的配准， 在缺少训练样本时或者实时性要求比较高时， 无法实现异源图像的快速鲁棒配准。

基于特征的图像匹配方法首先在待匹配图像之间寻找具有显著特征的点， 如角点、 线交叉点、 边缘点等， 然后利用特征点及其周围的像素形成特征点的特征表示， 最后再根据一定的搜索策略在特征表示之间寻找具有匹配关系的特征点。 由于考虑了特征点周围的统计信息， 并对特征向量进行了归一化， 因此能抵抗旋转、 光照和尺度变化。 基于特征的图像匹配方法中， 尺度不变特征变换（Scale Invariant Feature Transform，  SIFT）［5-7］最早被提出。 SIFT在高斯差分尺度空间（Laplacian of Gaussian，  LoG）中检测角点， 并利用特征点周围的梯度信息构造特征点的特征描述， 因此对一般的仿射变换都具有不变性， 但是受限于计算效率问题。  加速鲁棒特征（Speed-up Robust Features，  SURF）［8］和PCA-SIFT［9］以损失一定匹配精度为代价， 通过降低特征描述符的长度以实现对SIFT算法的加速。  BRIEF（Binary Robust Independent Elementary Features）［10］和ORB特征［11］也是以损失匹配精度为代价， 利用二值特征描述符减少描述符的占用空间并利用二值描述符的快速匹配策略加速匹配。  BRISK（Binary Robust Invariant Scalable Keypoints）［12］算法利用环形采样模式以解决BRIEF［10］算法存在的不能抵抗旋转差异的问题。  SAR-SIFT［13］利用比率梯度代替差分梯度， 从而增强SAR图像匹配的鲁棒性。 近年来， 国内一些学者提出了多种新的多模图像匹配方法， LSS［1］利用局部自相似性即图像块与周围区域的相关系数进行匹配， 可以实现具有相同区域模式图像的匹配。 CFOG［14］利用图像在多个方向上的变化率（多方向梯度）构造每个像素的特征表示， 可以实现多模图像匹配。 HOPC［15］和RIFT（Radiation-Variation Insensitive Feature Transform）［16］利用图像相位一致性提取图像的特征点， 可以实现具有非线性灰度变化的多模图像的鲁棒匹配， 但是对图像之间的旋转差异适应性差且运算量大。 HAPCG［17］利用各向异性加权力矩和绝对相位一致性方向直方图进行多模图像匹配， 提高了多模图像匹配的精度。

总而言之， 基于特征的图像匹配方法利用了特征点及其周围像素的统计信息， 在存在光照、 旋转和尺度差异的图像匹配上效果较好。 由于多模图像之间存在非常大的几何、 灰度、 时相差异， 因此使用SIFT等依赖梯度的方法并不能取得令人满意的效果。 较新的方法如HOPC［15］和RIFT［16］等不依赖于图像的梯度信息， 对具有非线性灰度差异的多模图像匹配效果较好， 但存在计算效率不高、 不利于工程应用的问题。 本文提出的基于RIFT［16］的二值描述符算法（Binary Descriptor for RIFT，  BRIFT）利用相位一致性和RIFT［16］算法中的最大索引图（Maximum Index Map，  MIM）， 结合BRIEF［10］算法中将特征描述符二值化的思想， 对RIFT算法计算效率不高的问题进行了改进， 将RIFT算法运算速度提高了一个数量级。 所提BRIFT算法首先利用快速算法在MIM上计算二值特征描述符， 然后利用Hamming距离作为测度进行特征匹配， 最后利用随机采样一致性算法［18］估算两幅图像之间的仿射变换矩阵， 从而剔除误匹配点， 实现多模图像的快速鲁棒匹配。

1相位一致性及特征描述符的快速计算

1.1相位一致性

使用相位一致性提取特征的思路来源于信号的Fourier分解， 考虑如图1所示的方波信号和三角波信号及其谐波分量。 在方波信号的阶跃位置和三角波信号的波峰波谷位置， 其谐波分量有近似一致的相位， 如谐波分量在方波阶跃位置相位均为0， 在三角波波峰波谷的位置相位均为0或者π， 而方波的阶跃位置和三角波的波峰波谷一般是信号中具有明显特征的位置。

相位一致性通过式（1）计算：

式中： ω0（x， y）为一频率扩展加权函数， 作用是当（x， y）处信号的频率分布较窄时对该位置进行惩罚， 即信号所包含的频率范围越宽， 其对相位一致性的贡献越大；  Aso（x， y）表示将图像I与尺度为s、 方向为o的log-Gabor正交滤波器Leven和Lodd卷积的幅度响应， 即

［Eso（x， y）， Oso（x， y）］=［I（x， y）*Leven（x， y， s， o）， I（x， y）*Lodd（x， y， s， o）］

log-Gabor滤波器定义在频域［19］， 其IFFT的實部对应滤波器的偶对称部分Leven， 虚部对应滤波器的奇对称部分Lodd；  ·」是为了防止所包含的部分为负数， 即当所包含的部分为负数时将其置为0；  ε为一个避免分母为零的小的常数；  T为一噪声阈值， 其作用是提高对含有噪声信号的特征检测能力；  ΔΦso为相位偏差函数， 其定义如下：

相比于式（1）中的相位偏差， 该定义下的相位偏差可以提供更好的特征定位能力。

根据式（2）， 为计算相位一致性， 需要将图像与多个尺度和方向上的log-Gabor滤波器进行卷积， 对于所有方向θo， 相位一致性的协方差矩阵为

根据矩分析理论， 最小矩mψ对应于图像中的角特征， 最大矩Mψ对应图像中边缘线特征。 由于最大矩Mψ图中非零元素更多， 因此可以检测到更鲁棒的特征。 本算法通过在最大矩图中执行FAST［20］检测得到特征点的位置。

1.2最大索引图及特征描述符快速计算方法

Li等［16］在RIFT算法中指出， 由于相位一致性图中大部分像素为0， 在相位一致性图上构造的特征描述符不足以完成多模图像的鲁棒匹配， 因此RIFT在最大索引图（MIM）上构造特征描述符。 最大索引图构造方式如图2所示，

其中：  A1～A6为将原图像在各尺度滤波结果相加， 得到在不同相角处的相位一致性； MIM为相位一致性最大处所在相角的索引。

在计算相位一致性时， 将图像与Ns个尺度和No个方向上的log-Gabor正交滤波器对进行卷积， 其幅度响应为Aso， 因此在给定方向o上的相位一致性Ao为最大索引图定义为所有No个方向中， 相位一致性最大的Ao所在的方向序号。 考察相位一致性的意义可知， 最大索引图实质上是将相位一致性方向量化到No个方向， 因此MIM（x， y）∈［1， No］。 RIFT算法［16］中通过实验确定使用Ns=4个尺度和No=6个方向以得到最优的结果。 为了与该算法对比， 所提BRIFT算法使用了相同的参数设置。

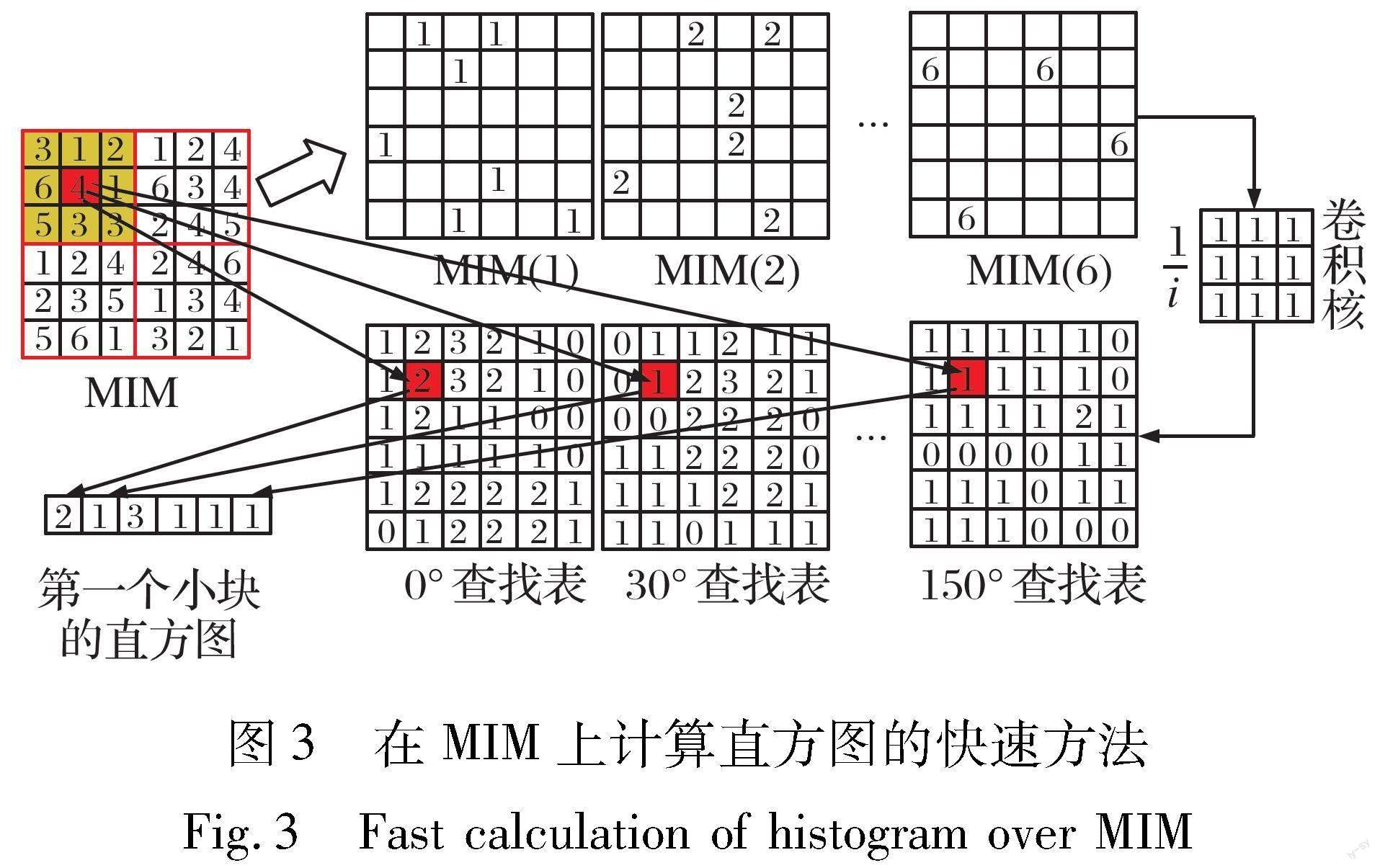
RIFT算法使用最大索引图构造特征描述符， 即对1.1节中检测到的特征点， 将以特征点为中心的图像区域切分为若干个block， 统计每个block的直方图， 将统计得到的直方图级联为一特征向量形成对特征点的特征描述。 然而， 统计直方图至少需要对每个block内的像素进行遍历， 时间复杂度为O（n）， 当特征点数量比较多时， 该步骤将耗费大量时间。 实际上， 由于MIM（x， y）∈［1， No］， 所以计算直方图可以通过盒式滤波简化为No次查表操作， 时间复杂度降低为O（c）， 具体如图3所示。 首先， 将MIM分解为No个子图， 每个子图仅包含相同的相位一致性方向索引。 其次， 将每个子图与求和滤波器进行卷积， 卷积核的大小与计算直方图的block的大小一致， 其中i表示方向索引。 因此， 卷积结果（查找表）中每个像素的值就表示以该像素为中心， 大小为block的范围内， 含有相同相位一致性方向索引像素的个数。 最后， 当需要计算某个block内的直方图时， 只需要在No个查找表上查找与block中心像素相同位置的元素值， 将这No个结果合在一起， 就构成了该block的直方图表示。 在实验部分， 对于含有5 000个特征点的图像（图像大小为500×500）， BRIFT算法可以节省约90%的计算时间。

2二值特征描述符

使用二值特征描述符的优势在于节省特征描述符的存储空间并加速特征匹配过程。 对于浮点数据类型的描述符， 在描述符长度相同时其占用空间约为二值化特征描述符的4倍。 其次， 浮点类型的特征描述符匹配需要计算浮点向量之间的欧氏距离， 由于现代计算机浮点数据的运算指令周期长于整型数据的运算指令周期， 因此特征匹配耗时更长， 而对于二值化的特征描述符， 特征匹配只需要计算特征描述符之间的Hamming距离， 即只需要将两个特征描述符进行异或操作即可， 可以大大节省特征匹配耗时。

2.1在MIM上应用BRIEF描述符

BRIEF［10］算法改进特征描述符的方式如下， 对于大小为S×S的像素区域p， 定义测试τ为

式中： I（p， x）为图像区域p中在位置x=（u， v）T处的图像灰度值。 通过选择nd个点对（x， y）， 就构成了区域p上的一个二值测试集， nd就是特征描述符的长度， 其BRIEF描述符定义如下：

BRIEF算法中给出了五种测试点对（x， y）的分布， 并指出当点对（x， y）相对于区域中心均服从高斯分布时， 所形成的二值描述符具有最高的识别率。 然而， 将BRIEF算法直接应用于相位一致性图或者最大索引图时， 均未取得期望的结果。 主要原因为： （1）将BRIEF算法应用于相位一致性图时， 由于相位一致性图中大部分像素均为0， 因此在给定的nd次测试下， 其结果也大部分为0， 因此形成的特征描述符可分性不高， 不能实现多模图像的鲁棒匹配；  （2）将BRIEF算法应用于最大索引图时， 由于多模图像之间非线性灰度差异较大， 因此两幅图像在相同测试点对处不一定有相同的相位一致性方向关系；  （3）将BRIEF算法应用于最大索引图时， 由于受到噪声等因素的影响， 单个点处的相位一致性方向可能并不准确， 其位置可能发生偏移， 从而造成该位置处的测试失效， 影响最终的匹配性能。

2.2新的二值化描述符

针对2.1节中直接将BRIEF算法应用于最大索引图所得描述符鲁棒性不足， 结合SIFT和RIFT等构造描述符的方式， 利用1.2节中所提的快速算法， 给出一种新的二值描述符构造算法。 对于大小为S×S的像素区域p， 将其划分为n×n个block， 每个block大小为m×m， 其中m=S/n。 在每一个block上定义测试τ为

式中： O（n）为每个block内相位一致性方向的主方向， 其可以通过1.2节所述方法获得， 则按照式（13）将区域p上的n×n个测试τ组和起来， 就构成了该区域中心处特征点的特征描述：

利用这种方法构造的特征描述符可以提供更好的鲁棒性， 这是因为每个测试都是在一个小的区域内完成的， 单个像素点处相位一致性方向产生的误差不会对整个小区域相位一致性的主方向产生大的影响。 此外， 由于可以使用1.2节方法快速计算每个block的主方向， 因此即使在p或n较大时， BRIFT算法也仍然可以取得优于RIFT算法的计算效率。

3實验

3.1数据集

本文实验数据［21］共包含光学-光学、 红外-光学、 深度-光学、 地图-光学、 SAR-光学、 白天-黑夜六组多模图像， 每组都包含了多个图像对， 共76对多模图像数据， 数据集中的部分数据如图4所示。

该数据集中的数据不仅涵盖了多传感器数据、 多时相数据， 还包含了地图数据；  图像的地距分辨率从0.1 m到数百米；  数据来源有卫星、 无人机等；  数据区域覆盖城区、 山地、 海岸等。 因此， 存在非常严重的辐射度畸变和局部几何畸变， 对多模态图像匹配而言存在巨大挑战。

为了评估算法性能， 从五个指标对匹配效果与匹配效率进行评估：

（1） 匹配点的个数（Number of Correct Match，  NCM）， 即进行外点剔除后两幅图像中匹配点对的数量。 由于每幅图像匹配点个数易受到外点剔除算法的影响， 因此NCM一般指每组数据的平均匹配点数， 即

式中： k表示该组数据集中图像对的个数；  NCMi表示第i对图像匹配点的个数。 实验中， 对于经过最近邻搜索得到的匹配点对， 使用文献［18］中的随机采样一致性算法剔除外点。 对于得到的仿射变换矩阵， 计算待匹配图像中同名点坐标在仿射变换矩阵转换下的坐标与参考图中同名点坐标的距离， 将距离小于3像素的匹配点对视为正确匹配点对。

（2） 匹配成功率（Correct Match Ratio，  CMR）。 精确的量化评估需要知道两幅图像之间的真实仿射变换矩阵， 然而， 由于受多种因素的影响， 实际的多模态数据集通常不含精确的对应关系， 因此需要在图像中选取多个均匀分布的点对以获得近似的仿射变换矩阵。 匹配点越多， 匹配点在图像上分布越均匀， 得到的近似仿射变换矩阵就越准确。 因此， 当两幅图像中的匹配点对非常集中， 或者当匹配点个数少于10时， 认为该匹配结果不正确。

（3） RMSE（Root Mean Square Error）， 其定义如下：

式中： （xi， yi）表示参考图像与待匹配图像的同名点坐标; （x′i， y′i）表示待匹配图像中的同名点坐标经仿射变换矩阵转换后的坐标。

（4） 匹配点的可分性（Ratio of Repeatability，  RR）， 即进行外点剔除后剩余匹配点对的个数与剔除前的比值， 该指标实际反映的是算法中每个描述符相对于其他描述符的显著性。

（5） 时间复杂度， 包括特征描述符计算时间与特征匹配时间。

3.2参数选择

影响BRIFT算法复杂度与匹配性能的参数有4个， 即计算相位一致性使用的log-Gabor滤波器的尺度个数Ns、 方向个数No、 计算特征描述符的区域大小S和每个block的大小m。 RIFT算法通过实验确定Ns=4， No=6。 使用本算法验证发现， Ns和No对匹配点数量的影响较小， 如在所有测试的4个方向个数（No=2， 4， 6， 8）中， 匹配点数量分别为340.60， 322.20， 311.90， 284.10， 变化不大， 这是因为本算法实际上将相位一致性量化到两个方向。 为了与RIFT算法对比， 将No设置为6， 但实际上将No设置得小一点可以获得更快的速度。

在区域大小S固定的情况下， 每个block的大小m影响计算描述符的复杂度， 也影响特征描述符的长度， 并最终影响匹配时间。 实验中， 将m分别设置为3， 4， 6， 8， 12， 16， 其结果如表1所示。 从表中可以看出， m越小， 描述符中每一bit的影响就越“局部”， 对区域的描述就更加细致；  描述符越长， 描述符之间的可区分度也更高， 正确匹配的点数就越多， 其代价是描述符计算时间的增加。 如m=3时， 描述符长度为（S/m）×（S/m）=1 024 bit（占用空间仍远低于RIFT描述符）， 其描述符计算时间约为m=4时（对应的描述符长度为576 bit）的1.4倍。 另外， m的值不宜设置过大， 除非区域S也非常大， 否则得到的描述过短， 对特征点的描述不精细， 描述符显著性严重降低， 将不足以完成多模图像的鲁棒匹配。 根据实验结果， 综合考虑算法的时间复杂度和匹配性能， 将m设置为4。

在block大小固定的情况下， 区域大小S也会影响描述符计算的时间复杂度和匹配性能。 实验中， 将S分别设置为48， 72， 96， 120， 144， 其结果如表2所示。 可以看到， 随着区域尺寸的增大， 描述符的长度变得更长， 因此描述符之间的可分性更强， 正确匹配点的个数也在增加， 但相应的描述符的计算时间也增加。 综合考虑算法的时间复杂度和匹配性能， 本文将S设置为96。

3.3與其他算法对比

图 5从左到右依次展示了SIFT， BRISK， BRIEF， RIFT， BRIFT算法的运行结果。 从结果来看， 对于多模图像， 由于图像对之间存在的非线性灰度差异和时相差异， SIFT算法和BRISK算法在所给的六组多模图像上均未取得正确的配准结果， 图中所给出的匹配点对也全部是误匹配。 直接在MIM上使用BRIEF算法（第三列）在部分多模图像上可以得到正确的结果， 但由于匹配点数远少于RIFT和所提BRIFT算法， 因此在另外的一些多模图像上匹配结果不理想， 如深度-光学、 白天-黑夜数据集。 RIFT算法在所给的六组多模图像上均取得了较好的配准效果， 但算法运行时间长， 计算量大， 不利于工程应用和实现。 所提BRIFT算法在六组多模图像数据集上也取得了较好的效果，虽然最终的匹配点对数量略小于RIFT算法，   如第三组深度-光学图像， 但通过这些匹配点对仍能得到正确的仿射变换矩阵， 对配准精度几乎无损失。

为了对比几种算法的优劣， 图6给出了SIFT， BRISK， BRIEF， RIFT， BRIFT在各数据集上匹配点个数（NCM）， 图7给出了各算法在各数据集上正确匹配图像个数的实验结果。 可以看到SIFT算法仅在个别图像上可以正确匹配， BRISK算法在所有图像上都未能匹配。 在MIM上使用BRIEF算法， 可以取得相对较好的效果， 但仍不及RIFT和所提BRIFT算法。 RIFT算法在所有的图像对上都可以匹配成功， 说明使用相位一致性进行多模图像匹配效果较好。 相比于RIFT算法， 所提BRIFT算法在NCM指标上略逊于RIFT算法， 在各数据集上其平均NCM约为RIFT算法的90.62%， 88.40%， 72.50%， 75.48%， 83.19%， 55.82%， 但正确匹配图像对的个数却与RIFT相差不大， 仅在红外-光学数据集（序号为1的图像对）和白天-黑夜数据集（序号为12的图像对）上有两幅图像未能正确匹配。 RIFT在这两对图像上的表现也同样不容乐观， 其NCM仅为20和37， 说明这两个图像对之间差异更大， 匹配更具挑战性。 BRIFT算法NCM指标低于RIFT算法的一个原因是RIFT算法在计算描述符时使用了归一化策略， 即将所有描述符按其L-1范数进行了归一化， 因此对非线性灰度变化的适应能力更强， 而所提BRIFT算法使用二值描述符， 没有归一化步骤， 因此在非线性灰度变化较大（如第六组白天-黑夜数据）时， 算法性能会出现一定下降。 其次， 由于在匹配时使用双向匹配策略， RIFT算法描述符在进行归一化后可分性更强， 而所提BRIFT算法使用的二值描述符受限于描述符的长度， 因此NCM指标不如RIFT。 NCM实际是与描述符长度正相关的， 这一点可以通过增加二值描述符的长度改善， 也可以使用多个大小的block从而形成多种长度的特征描述符进行匹配。 实际上， 对于图6中的所有图像对， 都可以通过增大区域S的大小和减小m的大小来构造更长的描述符， 从而达到优于RIFT算法的NCM指标。 如对于未能匹配的红外-光学数据集中序号为1的图像对， 如果将S设置为144， 将m设置为3， 此时描述符长度为2 304 bit， 占用空间仍低于RIFT算法， 其NCM可达到73左右， 从而成功匹配， 代价是描述符计算时间增加。

3.4时间测试

图8显示了RIFT算法与所提BRIFT算法在各数据集上的运行时长。 从实验结果可以看出， 所提算法在计算特征描述符时所用时间约为RIFT算法的12.2%， 特征匹配时间约为RIFT算法的53.66%。 因此， 在损失一定的NCM精度下， BRIFT算法使用的时间更少， 可以实现多模图像的快速鲁棒匹配。

4结论

本文提出了一种基于相位一致性和二值描述符的多模图像匹配方法。 该方法以MIM为基础， 通过盒式滤波器获得多模图像中每个像素点周围小范围内相位一致性的主方向， 然后将每个block的主方向根据其范围量化为1 bit符号， 通过在特征点周围选取若干个block构成特征点的二值描述符， 然后使用Hamming距离在特征描述符之间进行匹配， 最后通过随机采样一致性算法估计两幅图像之间的仿射变换矩阵并剔除误匹配点。 通过实验确定了BRIFT算法中所需参数的最优值， 并以此为基础与其他算法特别是RIFT算法进行了对比。 实验结果表明， 所提方法以损失少量匹配精度为代价， 将RIFT算法的运行速度提升了一个数量级， 提高了算法的执行效率， 实现了多模图像的快速鲁棒匹配。

参考文献：

［1］ Shechtman E，  Irani M. Matching Local SelfSimilarities across Images and Videos［C］∥IEEE Conference on Computer Vision and Pattern Recognition，  2007： 1-8.

［2］ Briechle K，  Hanebeck U D. Template Matching Using Fast Normalized Cross Correlation［C］∥ Optical Pattern Recognition XII，  2001，  4387： 95-102.

［3］ Chen H M，  Arora M K，  Varshney P K. Mutual InformationBased Image Registration for Remote Sensing Data［J］. International Journal of Remote Sensing，  2003，  24（18）： 3701-3706.

［4］ Haskins G，  Kruger U，  Yan P K. Deep Learning in Medical Image Registration： A Survey［J］. Machine Vision and Applications，  2020，  31（1）： 1-18.

［5］ Lowe D G. Object Recognition from Local ScaleInvariant Features［C］∥7th IEEE International Conference on Computer Vision，  1999： 1150-1157.

［6］ Lowe D G. Local Feature View Clustering for 3D Object Recognition［C］∥ IEEE Computer Society Conference on Computer Vision and Pattern Recognition，  2001.

［7］ Lowe D G. Distinctive Image Features from ScaleInvariant Keypoints［J］. International Journal of Computer Vision，  2004，  60（2）： 91-110.

［8］ Bay H，  Ess A，  Tuytelaars T，  et al. SpeededUp Robust Features （SURF）［J］. Computer Vision and Image Understanding，  2008，  110（3）： 346-359.

［9］ Ke Y，  Sukthankar R. PCASIFT： A More Distinctive Representation for Local Image Descriptors［C］∥ IEEE Computer Society Conference on Computer Vision and Pattern Recognition，  2004.

［10］ Calonder M，  Lepetit V，  Ozuysal M，  et al. BRIEF： Computing a Local Binary Descriptor Very Fast［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence，  2012，  34（7）： 1281-1298.

［11］ Rublee E，  Rabaud V，  Konolige K，  et al. ORB： An Efficient Alternative to SIFT or SURF［C］∥International Conference on Computer Vision，  2011： 2564-2571.

［12］ Leutenegger S，  Chli M，  Siegwart R Y. BRISK： Binary Robust Invariant Scalable Keypoints［C］∥International Conference on Computer Vision，  2011： 2548-2555.

［13］ Dellinger F，  Delon J，  Gousseau Y，  et al. SARSIFT： A SIFTLike Algorithm for SAR Images［J］. IEEE Transactions on Geoscience and Remote Sensing，  2015，  53（1）： 453-466.

［14］ Ye Y X，  Bruzzone L，  Shan J，  et al. Fast and Robust Matching for Multimodal Remote Sensing Image Registration［J］. IEEE Transactions on Geoscience and Remote Sensing，  2019，  57（11）： 9059-9070.

［15］ Ye Y X，  Shan J，  Bruzzone L，  et al. Robust Registration of Multimodal Remote Sensing Images Based on Structural Similarity［J］. IEEE Transactions on Geoscience and Remote Sensing，  2017，  55（5）： 2941-2958.

［16］ Li J Y，  Hu Q W，  Ai M Y. RIFT： MultiModal Image Matching Based on RadiationVariation Insensitive Feature Transform［J］. IEEE Transactions on Image Processing，  2019，  29： 3296-3310.

［17］ 姚永祥，  張永军，  万一，  等. 顾及各向异性加权力矩与绝对相位方向的异源影像匹配［J］. 武汉大学学报： 信息科学版，  2021，  46（11）： 1727-1736.

Yao Yongxiang，  Zhang Yongjun，  Wan Yi，  et al. Heterologous Images Matching Considering Anisotropic Weighted Moment and Absolute Phase Orientation［J］. Geomatics and Information Science of Wuhan University，  2021，  46（11）： 1727-1736.（in Chinese）

［18］ Li J Y，  Hu Q W，  Ai M Y. Robust Feature Matching for Geospatial Images via an AffineInvariant Coordinate System［J］. The Photogrammetric Record，  2017，  32（159）： 317-331.

［19］ Kovesi P. Image Features from Phase Congruency［J］. Videre： Journal of Computer Vision Research，  1999，  1（3）： 1-26.

［20］ Rosten E，  Porter R，  Drummond T. Faster and Better： A Machine Learning Approach to Corner Detection［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence，  2010，  32（1）： 105-119.

［21］ Zhang Y J，  Yao Y X，  Wan Yi，  et al.Research Resources［EB/OL］. （2022-03-14） ［2022-11-06］.https：∥skyearth.org/research/.

BRIFT： A Binary Descriptor for MultiModal Image Registration

Xu Kaikai，  Guo Pengcheng*，  Wang Jingjing

（Xian Electronic Engineering Research Institute，  Xian 710100，  China）

[HT]Abstract： Using radiationvariation insensitivity feature transform （RIFT） to calculate feature descriptors and perform feature matching on the maximum index map （MIM） is timeconsuming. To solve this problem，  an algorithm named binary descriptor for RIFT （BRIFT） is proposed. First，  the phase consistency of the image is calculated and the MIM is obtained. Then， the feature descriptor is calculated and binarized through fast algorithm on MIM. Finally，  the descriptor of each feature point is matched based on Hamming distance. Taking the remote sensing images with various geometric distortions and nonlinear radiation distortions as the test data，  the BRIFT algorithm is compared with other feature matching algorithms including SIFT， BRISK， BRIEF， RIFT. The comparison result shows that the proposed BRIFT algorithm can save about 80% to 90% of time consumption of feature descriptor evaluation and about 50% of feature matching time consumption with a slight loss of matching accuracy，  and achieve fast and robust matching of remote sensing images from different sources.

Key words： image matching; feature matching; phase consistency; maximum index map; binary descriptor