基于参考点之间水声传播的声速剖面反演
李鹏程,冯海泓,李记龙
(1.中国科学院声学研究所东海研究站,上海 201815;2.中国科学院大学,北京 100049)
0 引 言
影响水声目标定位、目标探测距离的一个重要因素就是水中的声速[1]。海水中的声速是对声传播有重要影响的海洋环境参数之一,在不同深度、不同地域会出现不同的声速梯度,声传播也会随着声速梯度的不同而发生变化,声线会向声速较小的方向发生偏转[2]。海洋中一定范围内的声速数据可以通过温盐深仪(Conductivity,Temperature,Depth,CTD)、声速剖面仪等设备直接测量获得。但是通过直接测量获取较大范围和较深海域的声速需要耗费大量的时间,并且需要投入较大的人力物力,难以满足实际中的需求[3]。
海水中的声速剖面反演研究为快速获取海区的实际声速剖面提供了新的有效方法,并且可以实现长时间的连续监测[4]。在声速剖面反演方面有许多学者进行了研究,Tolstoy等[5]将匹配场处理应用到海洋声层析中,对经验声速剖面进行经验正交函数分解,提取声速分布的特征,通过理论计算声场与实测声场进行匹配,最优声场匹配结果对应的声速作为声速反演结果。张忠兵[6]针对匹配场处理容易受到海底参数失配影响的问题,提出匹配波束反演方法,利用声信号到达接收点的时间差进行反演。唐俊峰等[7]采用微扰法,将声速剖面反演由非线性优化转化为线性方程组的形式,利用声信号的传播时间,提出了基于传播时间的声速剖面反演方法,以测得声信号到达接收阵的时间差构建代价函数,利用遗传算法全局优化性能得到最优结果。张维等[8-9]针对不平整海底反射时的传播规律,提出了一种三维空间特征声线搜索和声传播计算模型,研究了海底深度、声源位置和基阵倾斜等参数失配对声速剖面反演性能的影响。胡军[10]提出了基于径向基函数(Radial Basis Function,RBF)神经网络的声速剖面反演方法,利用RBF神经网络的逼近性能和自学习能力以及遗传算法的全局优化性能,得到最优参数的反演模型,实现了基于海表实测温度和历史数据的声速剖面反演。国家海洋局第二研究所研制了应用于近海的基于声线传播时间层析的海洋声层析仪,通过反演可以观测海域的温度、盐度、声速等海洋环境参数信息[11]。
海洋大地控制网是由一系列布设在海洋中的测量控制点构成的大地控制网,是国家测绘局布设的“2000国家大地控制网”的重要组成部分,由陆上、海面和海底三方面的控制点组成,其中最主要的是海底控制点[12]。海底控制网是海洋大地测量、海洋测绘和水下导航定位的基础,是海洋活动尤其是水下航行的重要参考基准,也是海洋权益维护、海洋资源勘探、海洋环境监测的重要基础设施[13]。海底控制点位置标定后,海底控制点、水中或水面声信号接收点及其相互间的声信号传输过程也为声速剖面反演带来了新的思路。本文将海底控制点作为水下固定参考点,通过研究利用水下固定参考点与水面已知位置之间的声信号传播时延来反演海水声速剖面的方法,尝试求解逆问题,建立一种针对目标海域进行快速、精确的声速剖面反演方法。
1 基本原理
1.1 声速反演模型建立
设水平方向上为x轴,垂直方向上为z轴,深度向下取正值,水面舰船的坐标为(xF,zF),根据海底参考点应答器的定位结果可以确定水下参考点应答器的坐标为(xB,zB)。声速在深度方向上的各层分布用C(z)表示,声线与深度垂直向下方向的夹角为θ(x,z),声信号从水下参考点应答器开始发射,经过时间τ被水面船只换能器基阵接收,如图1所示。
根据斯涅耳(Snell)定律:
k(xF)为一条声线所对应的常数。对于一条声线的传播时间,有:
水面船只和水下参考点应答器的水平距离为
根据式(1)中方程,可以得出:
代入式(2)、(3),声信号传播时间为
水面船只和水下参考点应答器的水平距离为
将水深等间距分为N层,水面船只接收声信号位置记为M,根据斯涅耳定律,可得:
将式(7)、(8)离散化[14-15],可得:
式(10)和(11)组成用来反演各层声速的非线性方程组,方程组中声信号传播时延τm,每层深度hn,水下参考点与水面测量点的水平距离xB-xFm都为已知参数;未知数为各层声速Cn和每条声线对应的常数值km。
1.2 牛顿迭代法求解非线性方程组
牛顿迭代法[16]是将非线性方程f(x)=0在x0点展开,即:
令:
用线性方程p(x)=0 近似代替非线性方程f(x)=0,再从p(x)=0 中解得x=x0-并令x1=x0-作为f(x)=0 的根的第一级近似值。同理,xk+1=xk-作为方程f(x)=0的根的第k+1级近似值,也作为牛顿迭代公式,xk为第k次迭代的初值。选取精度ε,判断若|xk-x0|<ε,则输出满足精度的解。
用牛顿迭代算法来求解由式(10)、(11)组成的非线性方程组,非线性方程组中方程的个数为2M,未知数为各层声速Cn和每条声线对应的常数km,未知数个数为M+N+1,方程个数和未知数个数相等时方程组可解,所以M=N+1,即水面船只声信号接收点的个数等于水深分层数加一。
声速反演的流程为:
(1) 将水中声速设为常数,即分为一层,水面选取两个关于水下参考点对称的测量点,通过迭代选取声线的初始入射角,确定该测量点对应声线的常数k;
(2) 重复M次步骤(1),确定2M个测量点处对应声线的k;
(3) 选取水下参考点其中一侧的M个水面测量点,将水深分为M-1层,将各层平均声速和每个测量点处的k作为初始迭代值代入,通过牛顿迭代法求解得到各层声速。
2 仿真计算
仿真环境采用2 维坐标,设水深为1 000 m,将水深等分为10 层,水下参考点坐标为xB=0。选取常见的声速剖面进行仿真验证,分别为负梯度声速剖面、正梯度声速剖面和C形声速剖面。
声速剖面为负梯度声速剖面时,设置的仿真参数如表1所示。设置好各层声速后,随机选取M个初始入射角,每条声线对应的常数k可由式(1)计算,因此仿真过程不需要选取水下参考点对称的点,水面测量点的位置和时延值可以由式(10)和(11)计算获得。建立关于声信号传播时间和接收位置水平距离的非线性方程组,将设置的声速加上50%的正态分布误差后作为迭代初始值,通过牛顿迭代法对非线性方程组迭代求解,解得各层声速如表2所示。

表1 负梯度声速剖面的仿真参数设置Table 1 Simulation parameter setting for negative gradient typed sound velocity profile
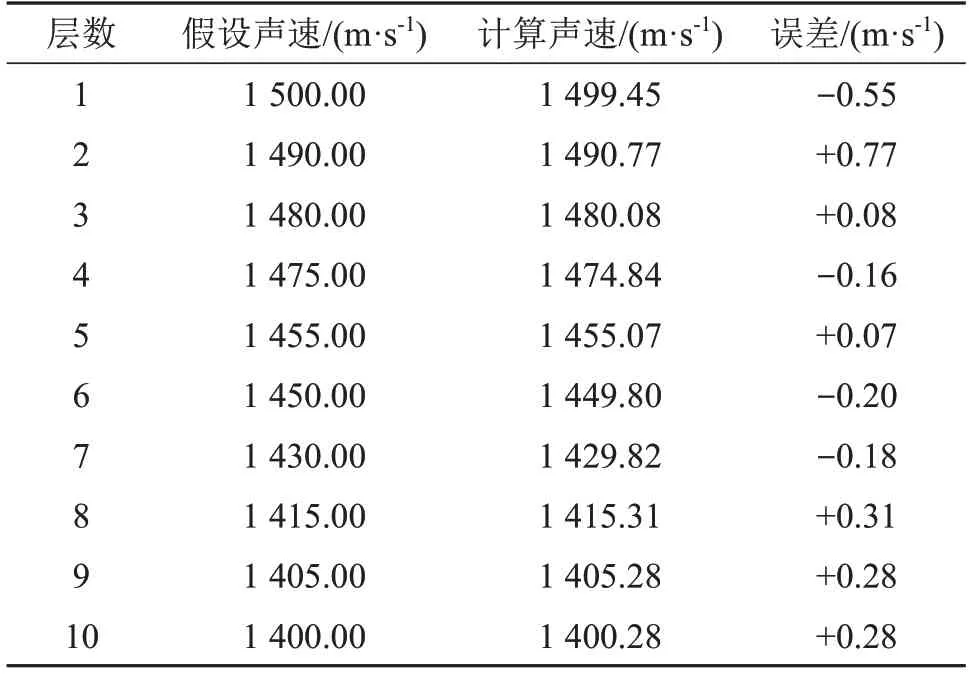
表2 各层反演声速与假设声速比较(对应于表1)Table 2 Comparison between inverted and assumed sound velocities of each layer corresponding to Table 1
声速剖面为正梯度声速剖面时,设置的仿真参数如表3所示。建立关于声信号传播时间和接收位置水平距离的非线性方程组,将设置的声速加上50%的正态分布误差后作为迭代初始值,通过牛顿迭代法对非线性方程组迭代求解,解得各层声速如表4所示。

表3 正梯度声速剖面的仿真参数设置Table 3 Simulation parameter setting for positive gradient typed sound velocity profile
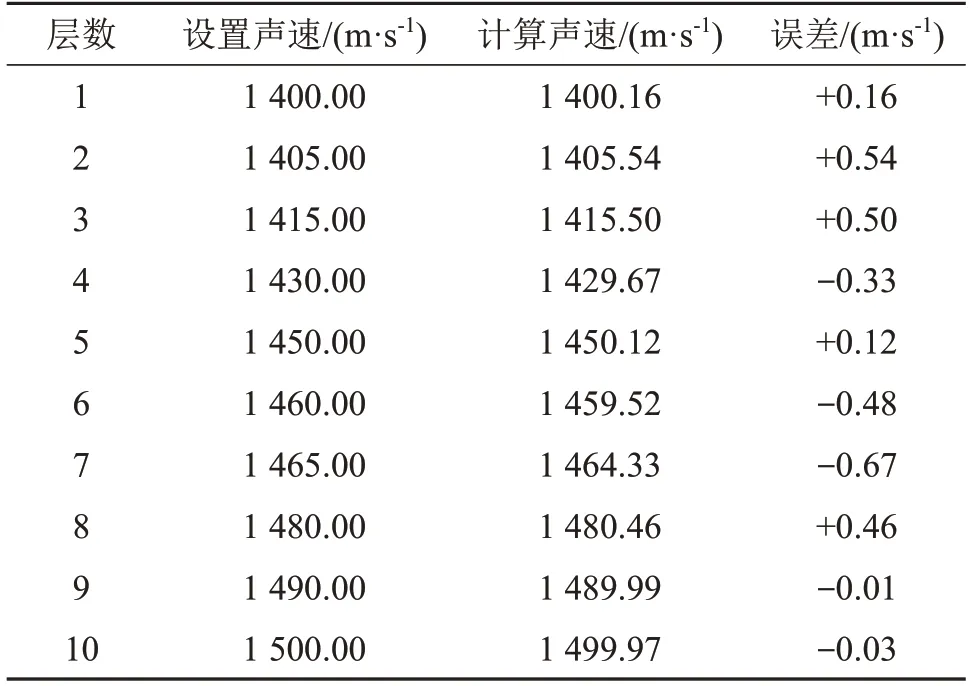
表4 各层反演声速与假设声速比较(对应于表3)Table 4 Comparison between inverted and assumed sound velocities of each layer corresponding to Table 3
声速剖面为C形声速剖面时,设置的仿真参数如表5所示。建立关于声信号传播时间和接收位置水平距离的非线性方程组,将设置的声速加上50%的正态分布误差后作为迭代初始值,通过牛顿迭代法对非线性方程组迭代求解,解得各层声速如表6所示。

表5 C形声速剖面的仿真参数设置Table 5 Simulation parameter setting for C typed velocity speed profile
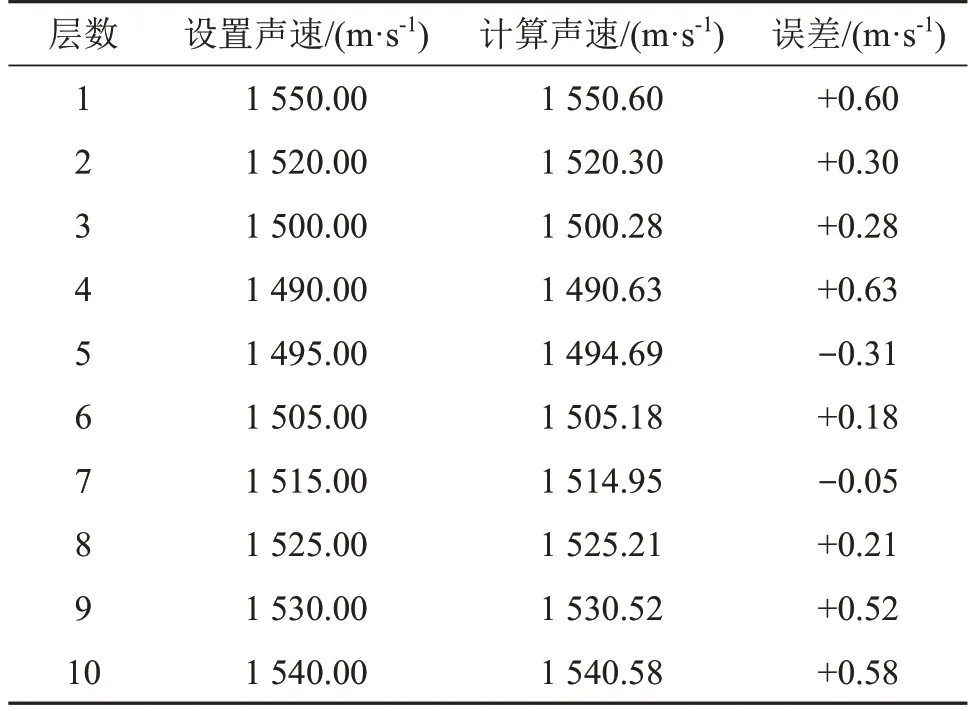
表6 各层反演声速与假设声速比较(对应于表5)Table 6 Comparison between inverted and assumed sound velocities of each layer corresponding to Table 5
对三种声速剖面进行了反演仿真,仿真得到的声速和仿真设置的声速相比误差较小。结果证明了反演模型的有效性。
3 海试数据验证
3.1 海试试验设计
试验数据来源于2021年5月某海上试验,在海上试验中,海况良好,试验海域的海底平坦,平均水深约为3 000 m,在海底布放1个可以发射声信号的潜标作为水下参考点,其中发射的声信号为8~16 kHz 的宽带复杂编码信号,发射周期为6 s。实验船底部有接收声信号的换能器基阵,船的位置可以通过GPS来精确定位,声信号在实验船底换能器基阵和海底应答器潜标之间的信号时延也可以精确测量,其中GPS 的定位精度为0.2 m,测时精度为50 μs。潜标标定完毕后,实验船的航行轨迹如图2所示。
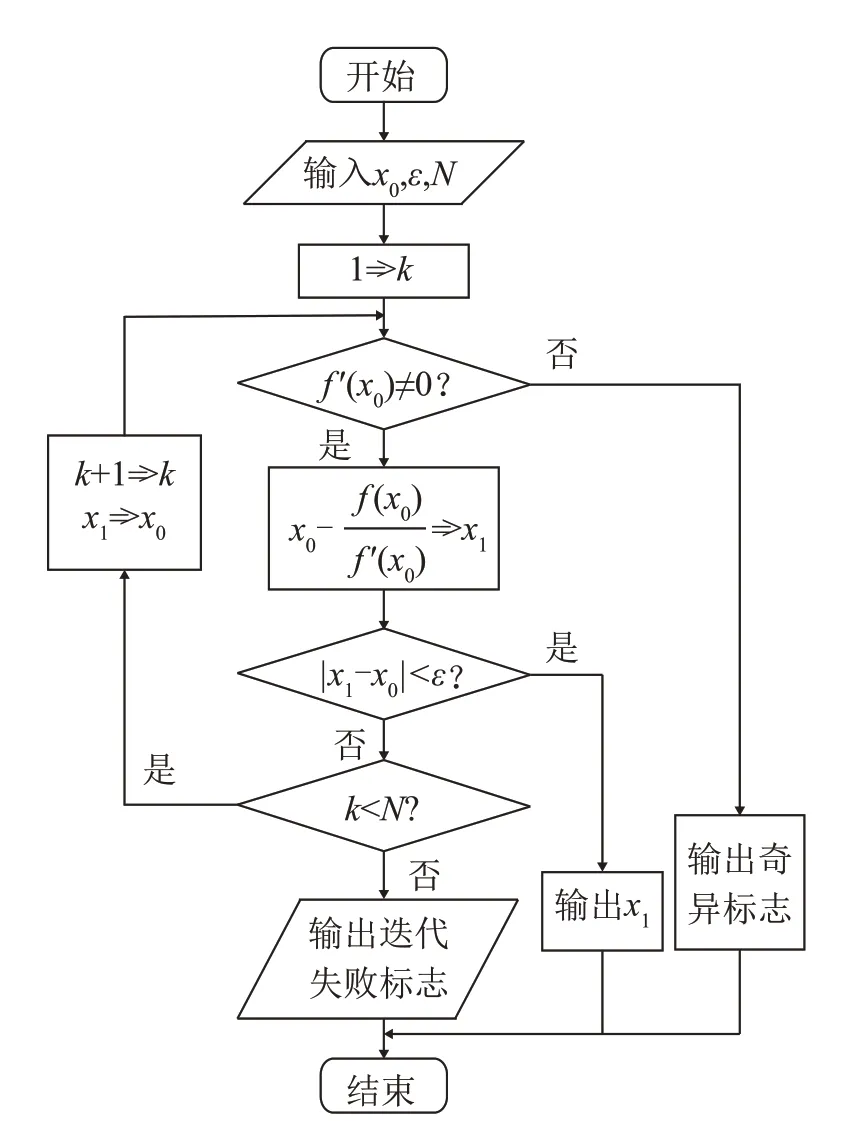
图2 牛顿迭代算法流程图Fig.2 Flow chart of Newton iterative algorithm
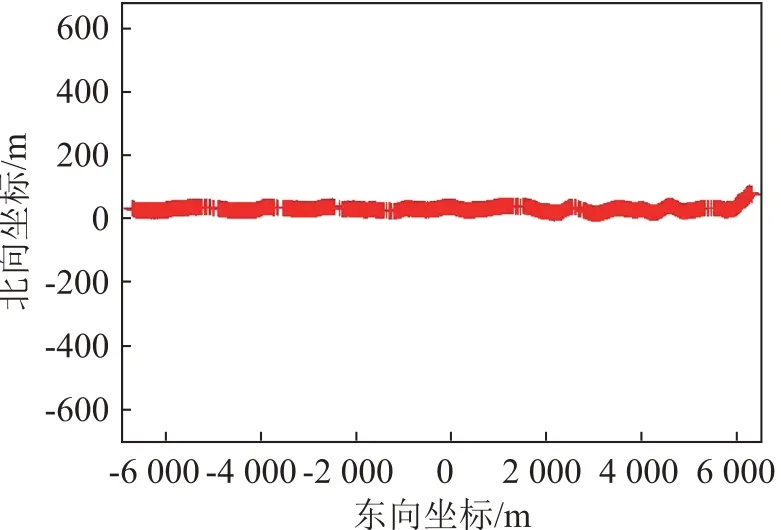
图3 实验船直线走航轨迹Fig.3 Straight route of the trial ship
3.2 声速反演
将潜标作为水下参考点应答器,并将潜标设置为坐标系的参考坐标系原点,在实验船航线上根据分层数来选择适量的测量点。
将水深等分为10层时,每层深度为300 m,水面船声信号接收点需要取11 个点。在潜标两侧分别选取与水下参考点的水平距离分别为1 000,1 500,2 000,2 500,3 000,3 500,4 000,4 500,5 000,5 500,6 000 m 处作为水面的测量点。将CTD 实测声速剖面数据按分的层数每层取平均,各层的平均值作为测量声速来和反演计算声速做对比,各层平均声速的计算公式为
通过前文反演流程中的步骤(2)迭代求得这11个测量点处的声线初始入射角和常数k。将测量声速加上50 %的正态分布误差后作为迭代的初始值,通过牛顿迭代算法迭代收敛得到各层水深的声速,结果如表7所示,计算声速与测量声速的平均误差为0.79 m·s-1。
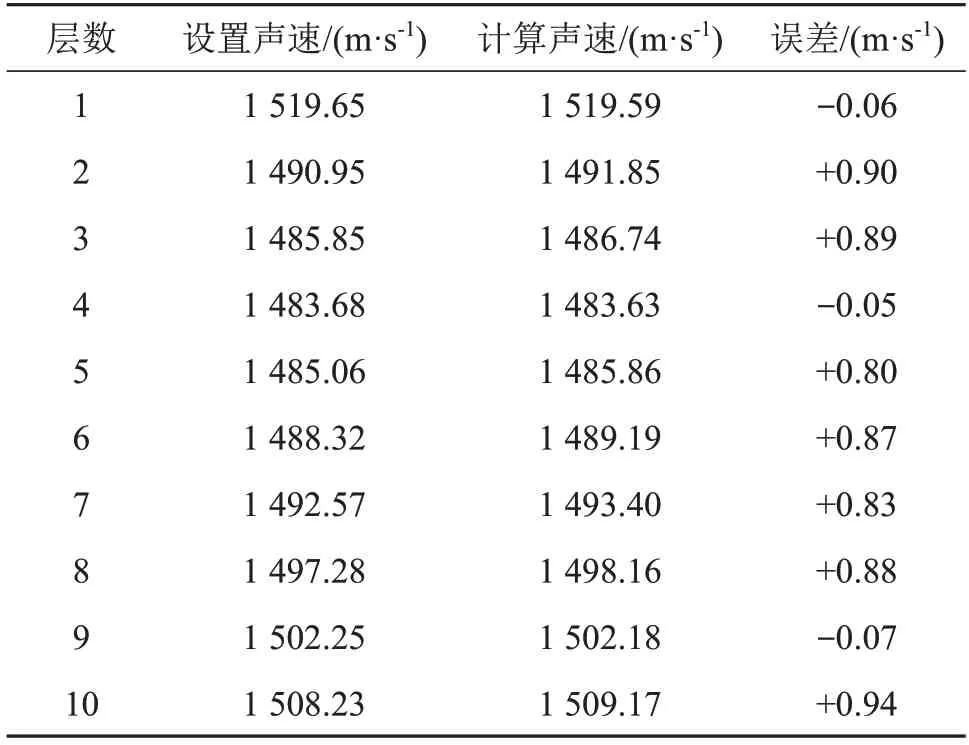
表7 各层反演声速与测量声速比较Table 7 Comparison between inverted and measured sound velocities of each layer
将水深等分为30层时,每层深度为100 m,水面船声信号接收点取31 个点。反演得到的声速剖面与实测声速剖面如图4所示。
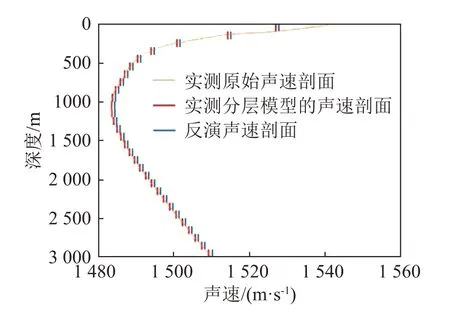
图4 反演声速剖面与真实声测剖面比较Fig.4 Comparisons between inversion and real sound velocity profile
在不同分层情况下,反演声速的平均误差如表8所示。将水深分为3~30层的过程中,反演的声速与实测声速之间的平均误差逐渐减小到0.8 m·s-1左右。分层数逐渐增加后,声速梯度包含更多层的声速信息,声速随深度的变化特征会更加明显、更加具体;在分层数较少时,声速梯度包含的声速信息较少,声速剖面每层之间的特征变化较大,不能完全体现声速随深度的变化特征,所以进行声速反演时误差较大。当分层增加到一定层数时,声速变化已经能够体现声速剖面的变化特征,而且在等声速分层模型中,误差只体现在各层的声速上,在牛顿迭代过程中近似值满足精度后输出的结果就是满足精度的声速,因此反演误差趋于稳定。
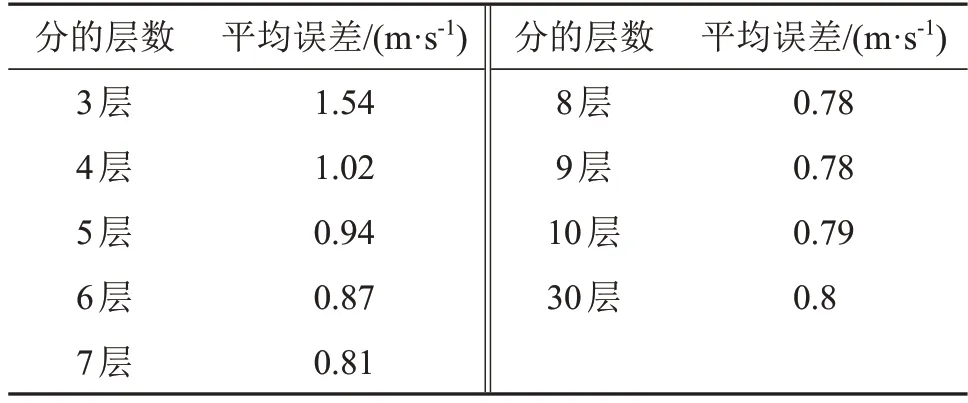
表8 不同的分层数对应的声速反演的平均误差Table 8 Average errors of sound velocity inversion corresponding to different numbers of layers
4 结 论
本文通过研究海底控制点定位的逆过程,提出了一种新的声速剖面反演方法。通过仿真验证了反演模型的有效性。再利用某海试数据对模型进行了进一步的验证,将水深分为3~30 层的过程中,反演的声速值与实际的声速值之间的平均误差会逐渐减小到0.8 m·s-1左右。但是随着分层数增加,非线性方程组变得越来越复杂,反演效率会逐渐下降。
由于解非线性方程组时要先确定解的范围,再确定精度,所以当初始迭代值改变时,迭代后的解会发生改变,迭代后的解是范围内满足精度的解,每次的解虽然不同,但是都在提前设的初始范围内,满足精度,误差小。针对初值选取的问题,还有待进一步的研究。

