变负载工况下滚动轴承故障分类识别方法研究

尹博文, 任 彬, 郝如江, 张建超

(石家庄铁道大学 机械工程学院,河北 石家庄 050043)

0 引言

机械故障诊断已进入“大数据”时代[1]。深度学习模型强大的特征提取能力以及对大批量数据的处理能力,使得基于深度学习的轴承故障诊断在近年来得到了广泛应用,并取得了很好的效果。YOU et al[2]提出了一种基于CNN和双向长短时记忆网络的(BiLSTM)的轴承故障诊断方法,获取滚动轴承故障特征的同时又防止了深度学习模型的过拟合;QIAO et al[3]提出一种基于卷积神经网络(CNN)和长短时记忆(LSTM)神经网络的双输入模型,利用原始振动信号和时频图对模型进行训练从而使用时域和频域特征来实现对滚动轴承的端对端故障诊断;徐先峰等[4]提出了一种基于CNN-LSTM的轴承故障诊断模型,实现了端对端的轴承健康状态分类。这些方法都利用了卷积神经网络强大的空间提取能力和长短时记忆网络处理序列信息的能力,具有很好的泛化性和鲁棒性,但单尺度的CNN往往对轴承故障特征提取不充分,并且在变负载的情况下滚动轴承的振动信号具有非线性特征,很难区分相同的故障类型[5],从而导致深度学习模型故障诊断的准确率降低。

为了充分提取变负载工况下滚动轴承振动信号的空间特征和时序特征,以适应现实工业生产中机械设备复杂多变工况,提出了一种双尺度卷积神经网络——长短时记忆网络(Dual-Scale Convolutional Neural Network—Bidirectional Long Short-Term Memory,DSCNN-BiLSTM)模型,通过设置2种不同变负载情况对该模型进行了变负载实验,验证了DSCNN-BiLSTM模型的可行性和泛化性。

1 DSCNN-BiLSTM模型理论

1.1 基础理论

1.1.1 粗粒度化

给定原始输入振动信号,粗粒度化的运算过程为

(1)

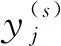
由式(1)可知,当s=1时,振动信号为其本身,以s=2和s=3为例,其运算过程如图1所示。

图1 粗粒度化过程

1.1.2 双向长短时记忆网络

双向长短时记忆网络(BiLSTM)[6]由正向LSTM和反向LSTM组成,其计算过程为

(2)

(3)

(4)

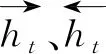
1.2 DSCNN-BiLSTM模型

DSCNN-BiLSTM模型只需输入原始振动数据,就可实现对滚动轴承的运行情况进行在线监测。其具体结构如图2所示,主要由双通道的卷积神经网络、BiLSTM层和全连接层组成。

图2 DSCNN-BiLSTM模型结构

在模型的第2通道,受粗粒度化原理启发,采用平均池化层来替换双尺度粗粒度层,在s=1时,通道输入为原始振动信号本身。s=2时,采用池化尺寸为2、步长为2的一维平均池化层,即当s=n时,用池化尺度为n、步长为n的一维池化层来代替双尺度粗粒度层。采取此种方式建立双通道输入对滚动轴承振动数据进行粗粒度化处理,充分提取其空间特征。其中平均池化层的计算过程为

(5)

DSCNN-BiLSTM模型采用一维卷积层、BN层和最大池化层来构建卷积神经网络模块,对滚动轴承振动信号进行空间特征提取。在卷积神经网络模块中,设置2个一维卷积层(Conv1D),每个一维卷积层后添加批量归一化层(BN层)并使用ReLu激活函数,在保证模型训练过程稳定的同时,也可以加快模型训练和准确率收敛的速度,防止梯度爆炸和梯度消失。

卷积层和最大池化层的运算过程为

(6)

(7)

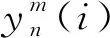
在卷积神经网络模块中,根据人工经验设置各个层的参数,如表1所示。

表1 卷积神经网络模块参数设置

经过双通道的卷积神经网络对滚动轴承数据进行空间特征提取后,使用concentrate层对两通道的数据进行特征融合,其运算过程为

(8)

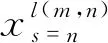
将融合后的特征输入到BiLSTM层中来提取滚动轴承数据的时序特征,并且在BiLSTM层后加入dropout层,来防止深度学习模型参数量过大导致的过拟合。其中BiLSTM层隐藏层单元数为128,设定dropout值为0.5。模型的最后为2个全连接层,第1个全连接层神经元个数为100,第2个全连接层神经元个数为训练数据的种类数,激活函数为Softmax。在模型编译中,采用Adadelta优化器,初始学习率为默认值1,衰减因子decay值为0.006,批大小为64,迭代次数为50。

2 实验验证

为了验证DSCNN-BiLSTM模型在变负载工况下的滚动轴承故障诊断的准确性和泛化性,采用美国凯斯西储大学(Case Western Reserve University,CWRU)和德国帕德博恩大学(Paderborn University)轴承数据集来设置2种不同的变负载情况作为DSCNN-BiLSTM模型的实验验证。

2.1 实验验证1

CWRU数据集试验平台[7]如图3所示,通过电机在不同负载工况下采集滚动轴承的振动数据。

图3 CWRU试验平台

实验采用采样频率为12 kHz的驱动端加速度数据,轴承损伤采用电火花加工的单点损伤,分别在电机0、746、1 492、2 238 W 4种负载工况下,对滚动轴承的正常状态、内圈故障、外圈故障和滚动体故障数据进行分析。因本数据集故障数据较少,且深度学习训练样本数较少时,训练模型识别性能将下降[8],故采用重叠采样方式,参考文献[9]样本处理方式,获取轴承在4种负载条件下的10种轴承健康状况数据,每种健康状况为600个样本,每个样本为1 000个数据点,得到每种负载情况下6 000个样本,共计24 000个样本。其中每种健康状况的轴承在不同负载条件下的标签为同一类别,如表2所示。

为了验证DSCNN-BiLSTM模型在变负载情况下的故障诊断精度,设定4种类型的负载任务进行实验,将4种不同负载情况下的数据进行划分,训练集和测试集比例为3∶1,如表3所示。

表3 CWRU数据集变负载实验设置 W

DSCNN-BiLSTM模型采用双尺度通道对滚动轴承振动信号进行双尺度特征提取,为验证DSCNN-BiLSTM模型中添加双尺度通道的可行性,调整和拆解模型结构进行对比实验分析:①CNN+BiLSTM[10],将DSCNN-BiLSTM模型第2尺度层通道去除,只保留s=1通道与BiLSTM衔接;②三尺度CNN+BiLSTM,在DSCNN-BiLSTM模型的基础上添加s=3尺度通道;③双尺度CNN,将DSCNN-BiLSTM模型中的BiLSTM层和dropout去除,在二尺度的卷积神经网络模块后添加Flatten层;④BiLSTM[11],将DSCNN-BiLSTM模型中的卷积神经网络模块去除,保留BiLSTM层。

在实验过程中,各个模型的超参数设置与DSCNN-BiLSTM相同,dropout率为0.5,批次大小为64,优化器为Adadelta,迭代次数为50次。采用Keras库和TensorFlow框架,计算机配置为Intel(R) Core(TM)i5-7300HQ CPU @ 2.50 Hz,NVIDIA GeForce GTX 1050Ti 显卡,8.0 GB运行内存。实验对比结果如表4所示。

由表4可知,DSCNN-BiLSTM模型的平均准确率分别比CNN+BiLSTM、三尺度CNN+BiLSTM、双尺度CNN和BiLSTM模型提高了2%、3.12%、8.62%和43.82%。

采用混淆矩阵方法进行故障状态识别,从而获取模型诊断的样本数据,为DSCNN-BiLSTM模型故障诊断结果提供可靠数据来源。如图4所示,横坐标轴为模型预测的滚动轴承健康状态标签,纵坐标轴为实际的滚动轴承健康状态标签。由图4(a)可知,负载任务A中,模型将33个标签为2的外圈-0.355 6 mm故障样本识别为了标签为8的滚动体-0.355 6 mm故障,12个标签为4的内圈-0.177 8 mm故障样本识别为了标签为2的外圈-0.355 6 mm故障。在负载任务B中,由图4(b)所示,模型预测标签与实际标签基本一致。在负载任务C中,如图4(c)所示,模型将138个标签为8的滚动体-0.355 6 mm故障样本识别为标签为2的外圈-0.355 6 mm故障。在负载任务D中,如图4(d)所示,标签为5的内圈-0.355 6 mm故障样本中有220个样本被模型识别为标签为8的滚动体-0.355 6 mm故障,28个样本识别为标签为4的内圈-0.177 8 mm故障,10个样本识别为标签为6的内圈-0.533 4 mm故障。另外模型将75个标签为4的内圈-0.177 8 mm故障识别为标签为6的内圈-0.533 4 mm故障,20个标签为8的滚动体-0.355 6 mm故障样本识别为标签为2的外圈-0.355 6 mm故障。

图4 CWRU数据集变负载实验混淆矩阵

2.2 实验验证2

选取德国帕德博恩大学数据集[12]进行变负载实验,其试验台如图5所示。

图5 德国帕德博恩大学试验台

选取不同的负载扭矩和轴承所受径向力数据作为变负载情况进行实验验证,其中损伤轴承采用电雕刻的单点损伤,损伤长度为1～4 mm,分为1、2共2种损伤程度,采样频率为64 kHz。因本数据集人为损伤轴承故障类型有限,故选取转速为1 500 r/min的正常轴承、轴承外圈故障程度1-2和轴承内圈故障程度1-2的振动数据作为实验数据进行验证。为了使每个样本尽可能多地包含滚动轴承振动数据的分布情况,设置每种类型的轴承健康状态数据样本数量为1 250个,每个样本为2 000个数据点。

变负载实验验证选取以下3种负载情况的滚动轴承振动数据:①负载情况A,负载扭矩为0.1 N·m,轴承所受径向力1 000 N;②负载情况B,负载扭矩为0.7 N·m,轴承所受径向力400 N;③负载情况C,负载扭矩为0.7 N·m,轴承所受径向力1 000 N。

样本设置如表5所示。

表5 帕德博恩大学数据集变负载工况样本设置

与2.1节凯斯西储变负载实验类似,选用其中2种负载情况作为训练集,另一种负载情况为测试集。负载任务分布如表6所示。

表6 帕德博恩数据集变负载实验设置

与CWRU变负载实验相同,分别用DSCNN-BiLSTM模型与上述几种模型进行对比,实验结果如表7所示。

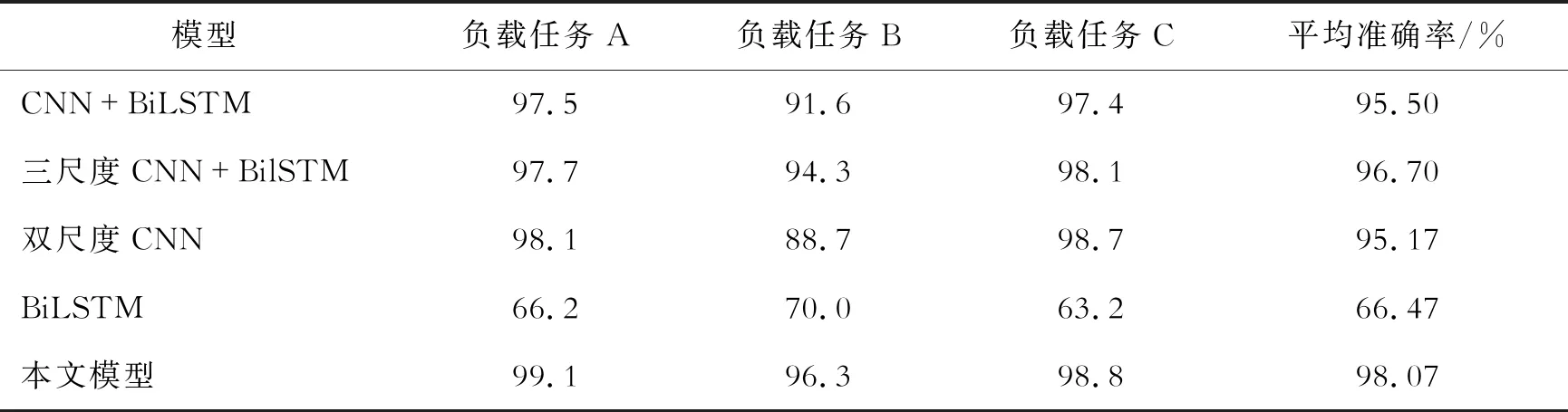
表7 帕德博恩大学数据集变负载实验模型对比

由表7可知,DSCNN-BiLSTM模型的平均准确率分别比CNN+BiLSTM、三尺度CNN+BiLSTM、双尺度CNN和BiLSTM模型提高了2.57%、1.37%、2.9%和31.6%。

如图6所示,在图6(a)中,各个健康状态的滚动轴承样本均有混淆,但预测标签与实际标签不一致的数目相当于总体样本数目较少。在图6(b)中,模型主要将206个标签为4的内圈故障-2样本识别成标签为0的正常状态轴承。在图6(c)中,模型主要将43个标签为4的内圈故障-2样本识别成标签为1的外圈故障-1轴承。

图6 帕德博恩大学数据集变负载实验混淆矩阵

综上所述,通过2组实验验证表明了DSCNN-BiLSTM模型能够较好实现滚动轴承的故障分类与状态识别,为滚动轴承的智能故障诊断与预测研究提供了关键技术。

3 结论

针对变负载工况下单尺度CNN提取滚动轴承健康状态特征不充分的问题,提出了一种基于DSCNN-BiLSTM的滚动轴承故障诊断模型。得到结论如下:

(1)DSCNN-BiLSTM模型采用两通道的卷积神经网络模块与双向长短时记忆网络相结合,可以在空间上提取滚动轴承振动信号的双尺度特征,并由双向长短时记忆网络提取其时序特征,实现了端对端的滚动轴承故障诊断。

(2)通过设置2种不同变负载情况对DSCNN-BiLSTM模型进行了变负载实验,模型的平均准确率分别为97.55%和98.07%,有效提高了在变负载工况下的滚动轴承故障诊断准确率。