S型齿廓齿轮滚铣2步加工技术研究

田宇宙, 孙 强, 吴建伟

(石家庄铁道大学 机械工程学院,河北 石家庄 050043)

0 引言

随着齿轮传动应用的不断深入,传统渐开线齿轮已然满足不了一些特殊场合的需求,越来越多的新型齿轮应运而生。其中新型LogiX齿轮[1]、分阶式双渐开线齿轮[2]、渐开圆弧齿轮[3]、余弦齿轮[4]、S型齿廓齿轮[5]等为典型的新型齿廓齿轮,新理论的出现也给实际加工带来了难题。新型齿轮理论的提出一定要以实际应用为目标,所以寻求特殊齿廓齿轮通用型加工方法是研究的关键。

KAWASAKI et al[6]针对双斜齿轮的加工,提出了基于计算机辅助系统的三轴数控加工中心的加工方法,不需要专业刀具即可完成齿轮加工并进行了误差测量和寿命评估。LI et al[7]首次提出并建立了非圆齿轮成形的数值模型,并利用电磁放电(EMD)成功地加工了齿轮。该方法具有一定的通用性,适用于任何节线,为非圆齿轮加工开辟了新的前景。国内学者对齿轮加工技术的研究也取得了长足的进步。FENG et al[8]提出了基于渐开线齿轮滚刀,在双向正交联动变位理论支持下,由CNC滚刀柔性控制刀具和工件间的创成运动来实现特殊齿形的加工。于晨伟等[9]针对椭圆弧齿线圆柱齿轮的加工提出了倾斜式旋转刀盘加工方法,并建立刀具仿真模型验证其方法的可行性。谢云汉[10]为提高直齿锥齿轮的加工效率,提出了一种可以进行连续展成的滚齿加工方法,并进行仿真加工验证了其可行性。唐进元等[11]根据齿轮插齿原理对面齿轮设计了一种多线包络加工的方法,并进行了刀具轨迹规划与数控加工仿真,得到了一种新的面齿轮加工方法。针对线接触曲线圆柱齿轮,张学刚等[12]提出一种采用现有六轴数控铣齿机和单刃面铣刀盘的线接触曲线齿轮加工方法。任建平等[13]为解决传统弧面锥齿轮加工质量难以控制的问题,从加工理论和机床性能方面提出了一种小模数弧齿锥齿轮半滚切加工方法,提高了齿面啮合质量。罗善明等[14]创造性地将滚齿与铣削加工结合起来,分步对余弦齿廓进行加工,得到了基于普通加工方法对特殊齿形进行加工的通用方法,为特殊齿廓的大批量加工开辟了新的思路。

现针对S型齿廓曲线的加工,拟采用更适用于通用加工的滚切和铣削加工相结合的2步加工思路。该方案无需专用机床和刀具,加工简单,通用性强,为今后S型齿廓齿轮的实际应用奠定了基础。

1 滚切加工数学模型

1.1 S型齿廓齿轮数学模型

S型齿廓成形机理为用正弦曲线代替直线进行包络加工形成齿廓。由文献[15]得,其通用数学模型如下

(1)

(2)

(3)

由S型齿廓刀具产生机理[16]可知,当衍生系数为0时,齿廓为渐开线形。所以相同参数下的S型齿轮和渐开线齿轮齿厚在分度圆是一致的,但是其他位置齿厚完全不同,所以不能在渐开线齿廓基础上铣削得到S型齿廓,即在加工时要考虑变位系数。

考虑到刀具的通用性、加工效率及成本等因素,在第1步齿坯粗加工时采用滚齿加工。

为方便下文计算,现将S型齿廓模型简化如下

F[x(m,α,Z,λ),y(m,α,Z,λ),z(m,α,Z,λ)]=0

(4)

1.2 最小变位系数的确定

确定最小变位系数xrmin,就是保证渐开线齿厚在任意圆处至少大于S型齿廓齿厚,即在后续加工不产生干涉或过切。S型齿廓与渐开线齿廓对比示意图如图1所示。

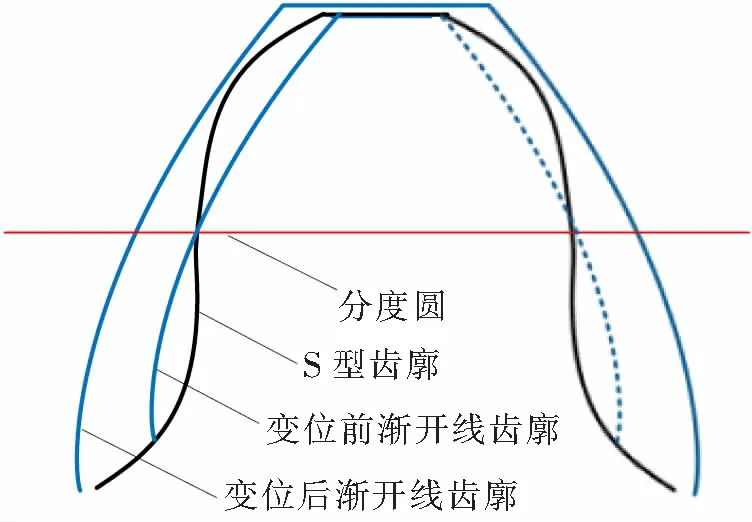
图1 S型齿廓与渐开线齿廓对比示意图

为方便计算,可比较基圆处的齿厚。

S型齿廓在基圆处齿厚Ssb为[17]

(5)

式中,rb为基圆半径;xsb、ysb分别为基圆与S型齿廓交点横纵坐标。

渐开线齿廓在基圆处的齿厚Sjb为

(6)

式中,z为齿数;xr为滚切加工径向变位系数;αb为基圆处压力角。

二者满足条件为Sjb≥Ssb。

将式(5)、式(6)代入上述齿厚关系,得到径向变位系数的范围为

(7)

即最小变位系数xrmin为

(8)

上述得到的就是滚齿加工的最小变位系数,同时也达到了尽可能减少加工量的目的,提高了加工效率。考虑到加工余量和过渡圆弧干涉可适量增加0.1～0.2。

2 铣削加工运动控制模型

2.1 坐标系的建立

S型齿廓加工处于初期研究,所以从加工较为简单直齿齿轮出发,故铣削加工采用三轴数控加工铣削即可完成,坐标系建立如图2所示。

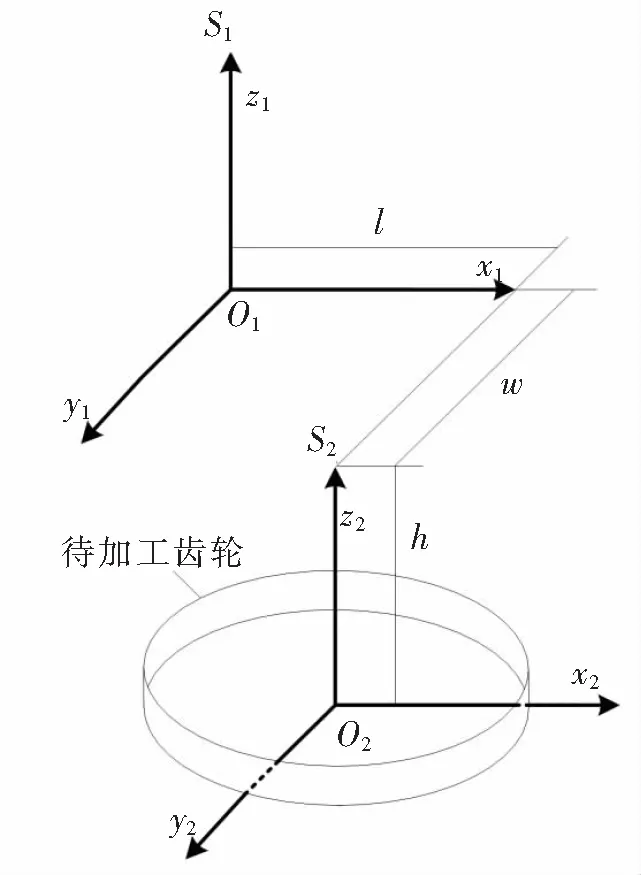
图2 铣削加工坐标系

图2中,S1、S2分别为铣刀固连坐标系和工件固连坐标系;O1、O2分别为对应坐标系原点;l、w、h分别为x、y、z方向的进给量。

铣削加工过程中主运动为铣刀的回转运动,与待加工齿轮相切达到铣削的目的。进给运动主要包括铣刀在齿轮轴向、径向和切向3个方向的进给运动。3个方向联动配合最终加工得到目标齿廓。

2.2 空间变换矩阵

数控铣床加工时,必须将铣刀坐标系转换到工件坐标系下进行,才能将所需齿廓形状加工完成。空间转换矩阵如下

(x2,y2,z2,1)T=M12(x1,y1,z1,1)T

(9)

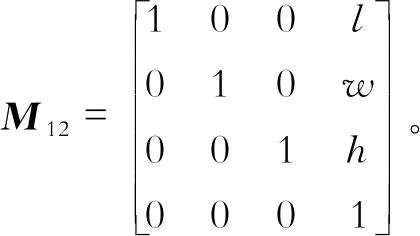
故铣刀轨迹坐标(x1,y1,z1)根据式(10)即可求得。

(10)

3 S型齿廓铣削加工数学模型

由上述坐标系的确立可知,对齿轮进行铣削加工时,铣刀轴线与齿轮轴线平行并对齿轮进行轮廓铣削,所以铣刀选择轮廓铣削最常用的球头铣刀。

S型齿廓铣削示意图如图3所示,使得球头铣刀的中心运动轨迹落在S型齿廓的法向等距曲线上,所对应的区域即完成铣削加工,铣刀中心的轨迹坐标即为所求。

图3 S型齿廓铣削模型示意图

如图3所示,首先得到p点矢量rp

rp=(xp,yp,zp)

(11)

式中,xp、yp、zp满足式(4),接着求出p点法向量n

n=(xn,yn,zn)

(12)

式中

(13)

式中,Fx为函数F在p点对x的偏导数;Fy为函数F在p点对y的偏导数;Fz为函数F在p点对z的偏导数。

根据矢量关系铣刀中心轨迹可表示为

rBo=rp+Rn

(14)

式中,R为铣刀半径。

将式(11)～式(13)带入式(14),可得刀心轨迹坐标Bo(xBo,yBo,zBo)。

(15)

因从初期的S型齿廓直齿齿轮加工出发,故只需考虑x,y2个方向的运动,对于z轴方向只需均匀平移进给即可。

将整个齿廓分为齿侧、齿顶及齿根过渡圆弧部分,分别进行模型分析。

3.1 S型齿廓齿侧加工数学模型

齿侧铣削加工数学模型如图4所示。

图4 S型齿廓齿侧铣削模型示意图

图4中,α为齿侧上任意一点p的法向量与x轴正向夹角,满足以下关系

(16)

式中,Kn为p点法向量所在直线斜率;Kτ为p点切线斜率;F、x、y满足式(4)。

将式(16)带入式(14)可得S型齿廓齿侧铣削刀具中心坐标为

(17)

式中,ΔT为总的加工余量;ΔTi为第i次法向进给量。

3.2 S型齿廓齿顶加工模型

齿顶圆弧铣削加工数学模型如图5所示。

图5 S型齿廓齿顶圆弧铣削模型示意图

图5中,β为齿顶上任意一点p的法向量与x轴正向夹角,满足以下关系

(18)

式中,Kn为p点法向量所在直线斜率;Kτ为p点切线斜率;F、x、y满足式(4)。

(19)

式中,ra为齿顶圆半径;θ1为参数。式(19)为齿顶圆参数方程。

将式(18)带入式(14)可得S型齿廓齿顶圆弧铣削刀具中心坐标为

(20)

3.3 S型齿廓齿根过渡圆弧加工数学模型

齿根过渡圆弧加工数学模型如图6所示。

图6 S型齿廓齿根过渡圆弧铣削模型示意图

如图6所示,S型齿廓与过渡圆弧相切,假设过渡圆弧半径为r,则其参数方程如下

(21)

式中,xa、ya为过渡圆弧中心坐标;θ2为圆弧参数。

图6中,γ为过渡圆弧上任意一点p的法向量与x轴正向夹角,满足以下关系

(22)

式中,Kn为p点法向量所在直线斜率;Kτ为p点切线斜率;F、x、y满足式(4)。

将式(22)带入式(14)可得S型齿廓过渡圆弧铣削刀具中心坐标为

(23)

综上,式(17) 、式(20) 、式(23)分别得到了S型齿廓齿侧、齿顶及过渡圆弧部分的刀具中心坐标,即完成了一个齿单侧的铣削加工。所以通过坐标的对称及旋转变换即可得到整个齿轮的刀具加工坐标,之后转换到数控铣床所对应的坐标即可完成加工。

4 实例分析及仿真加工

现以模数m=2、齿数z=20、压力角=25°的S型齿轮为例进行加工仿真。

4.1 滚切加工

首先进行粗加工,为最大程度去除加工余量,提高工作效率,按照式(8)并带入数据计算得到的最小变位系数xrmin=0.109,考虑到齿根过渡圆弧的干涉以及加工余量,现确定滚切加工径向变为系数为xr=0.3,求解出变位后的渐开线齿形并画图,如图7所示。

图7 变位渐开线齿廓与S型齿廓加工对比图

如图7所示,变位渐开线齿廓完全包裹S型齿廓,并预留了刀具加工余量,符合数学模型及预期要求。

4.2 铣削加工

在得到变位渐开线齿轮基础上进行铣削加工仿真。首先,已知分析案例的S型齿廓过渡圆弧直径为1.2 mm,考虑到铣刀尺寸的通用性及与被加工圆弧尺寸关系,所以铣刀选择为直径1 mm的球头铣刀。

严格按照上述建立的S型齿廓铣削加工数学模型对铣削过程进行计算机仿真。

第1步利用Matlab进行刀具铣削的轨迹仿真以验证基于上述S型齿廓加工数学模型的有效性。具体仿真过程如下:基于S型齿廓方程在Matlab中进行数据离散,求出齿面方程的法向等距曲线作为铣刀的中心轨迹所在曲线,然后进行刀具铣削轨迹的绘制从而得到S型齿廓曲线。基于上述仿真过程的刀具轨迹仿真图如图8所示,从图8可以看出,无欠切和过切现象,进一步证明了数学模型的正确性和加工方法的可行性。仿真第2步,利用三维软件分别对变位渐开线齿轮和S型齿廓进行参数化建模,如图9所示。基于三维软件的数控加工模块进行S型齿轮的齿廓铣削仿真加工,刀具中心铣削轨迹如图10所示。

图8 铣削加工S型齿廓刀具中心轨迹仿真图

图9 变位渐开线齿轮与S型齿廓齿轮参数化建模

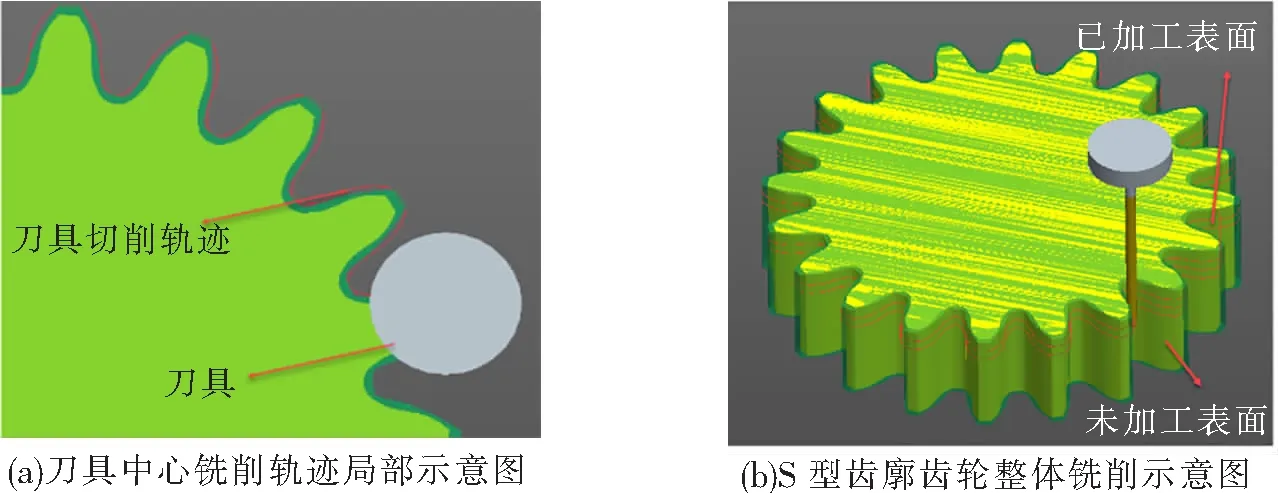
图10 S型齿廓齿轮铣削仿真图

由仿真结果可知,与理论数学模型以及Matlab仿真结果相一致,具有良好的铣削效果。在此基础上生成铣刀铣削ncl文件,处理后可得到用于后续数控铣床加工的tap文件,为后续的实物加工打下基础。

5 滚铣2步加工方法误差分析

滚铣2步加工方法为分步式加工,误差来源主要为滚切加工与铣削加工。

对于滚切加工,由文献[18]可知,综合考虑机床运动误差、刀具几何与安装误差,得到映射在齿廓上的几何误差范围为10～20,而本文所研究加工方法为分步加工,在滚切加工后所产生的加工误差会被铣削加工所去除,且铣削加工去除量远大于10～20。因此,滚切加工误差可忽略。

对于铣削加工,加工误差主要来自机床本身误差,包括零件几何误差、坐标轴对齐误差、热变形误差等[19-20]。这些误差均可以通过对机床定期维护、加工前的调零与检查等来进行有效控制。而对于本文加工方法在控制误差上还有以下几点优势:①加工对象为强度较大的齿轮,非轻薄件,对于装夹误差的控制较为容易;②在铣削加工时,只存在铣刀的运动控制,避免了工件与铣刀的相对运动误差(顺铣与逆铣);③在整个铣削过程,铣刀只需装夹一次即可完成铣削,避免了重新对刀的误差,且齿轮齿厚较小,减少了刀具过长因径向力产生的挠度偏差。

综上,对于滚铣2步加工方法的误差均为可控的,对于精度有一定的保证,所以该加工方法是可行的。

6 结论

基于一种新型S型齿廓提出了一种通用性较强的滚铣2步加工方案并进行了理论案例分析及仿真,主要得出以下结论:

(1)选择普通滚齿加工与铣削加工组合,很好地解决了S型齿廓的高效加工问题,考虑加工误差后具有较强的可实施性。

(2)因S型齿廓加工理论处于初期,所以只研究了直齿齿轮的加工,为后期的斜齿齿轮加工理论做了一定的铺垫。