分布式驱动电动汽车多电机系统改进型环形耦合控制

吴宇航, 许鸣珠

(石家庄铁道大学 机械工程学院,河北 石家庄 050043)

0 引言

随着现代科技的发展,电动汽车逐渐普及。传统的电动汽车采用中央式驱动的形式[1],需要传动装置将动能从中央电机传递到每个车轮,传递过程造成了动能浪费。由轮毂电机驱动的电动汽车采用轮毂电机作为动力源,对电动汽车的4个车轮进行独立驱动,摆脱了传统集中驱动汽车传动效率较低的问题,大大减少了传动过程中的损耗[2]。采用独立轮毂电机驱动要求车辆对电机有更加精准的控制能力,同时要求4个车轮有很好的同步性能[3]。各轮毂电机之间的协同控制非常重要,已经成为电动汽车研究的热点方向之一。

在轮毂电机的协同控制中,各轮之间的同步精度和跟踪精度是影响四轮独立驱动电动汽车稳定性的重要因素,也是衡量控制形式优越的重要指标。

多电机之间的协同控制形式可分为非耦合控制和耦合控制。非耦合控制主要包括主从控制、并行控制以及虚拟主轴控制[4],在非耦合控制中各电机之间没有信号的反馈和补偿,末端信号反馈到自身的控制器上,通过设定的初始值来达到各电机之间的同步。非耦合控制的优点是结构简单容易实现,但其同步精度较差,难以完成四轮独立驱动电动汽车各轮电机之间的协同控制要求。

耦合控制目前主要包括偏差耦合控制[5]、环形耦合控制[6-8]、相邻耦合控制[9]、相对耦合控制、组合交叉耦合控制[10]、协调耦合控制[11]。在耦合控制中,各电机之间建立相互联系,末端信号不仅反馈到自身的控制器中,还会通过速度控制器或直接反馈到其他电机的控制器中,实现多电机之间的耦合控制。耦合控制形式下各电机之间相互联系,同步精度以及跟踪精度较高,有利于多电机协同,适合轮毂电机驱动的电动汽车。

偏差耦合控制以建立所有电机之间连接的方式控制各个电机之间的同步精度[4],实际跟踪精度较高,但是各个电机之间的联系复杂,在要求高精度同步的情况下,系统可能不够稳定。文献[12]提出了一种改进型相对耦合控制形式,在偏差耦合的基础上为每一个电机附加优先级系数,但是响应速度比较慢。文献[13]改进了相邻耦合控制方法,降低了控制器的复杂性,被控系统的稳定性得到了提高,但响应速度在四轮独立驱动电动汽车的多电机协同控制中并不理想。

轮毂电机独立驱动电动汽车各轮之间的同步精度和跟踪精度需要同时得到保证,环形耦合控制建立了每台电机之间的耦合关系,可以在降低同步误差的同时保证跟踪精度,且控制系统的复杂性较低。现针对高性能永磁同步轮毂电机(PMSM,permanent magnet synchronous motor),选择环形耦合控制方法对其进行控制研究。设计了基于傅里叶级数循环学习[14]的改进型环形耦合控制方法。通过Simulink仿真初步验证该算法的有效性。然后,利用CARSIM搭建整车模型和Simulink进行联合仿真,进一步验证其在实车控制中的可行性。

1 三相PMSM的数学建模

为简化PMSM分析研究,假设PMSM能够满足以下3个条件:

(1)电机铁芯饱和忽略不计;

(2)电机中的涡流和磁滞损耗忽略不计;

(3)电机中的电流为对称的三相正弦波电流。

则PMSM在同步旋转坐标系下的电压方程为

(1)

通过同步旋转坐标系后,电机的转矩方程为

(2)

式中,ud、uq分别为定子电压d-q轴分量;id、iq分别为定子电流的d-q轴分量;R为定子电阻;ωe为电角速度;Ld、Lq分别为d-q轴的电感分量;φf为永磁体磁链;Te为电机转矩。

将坐标系同步旋转后,电机的矢量控制通过控制定子电流的大小和方向实现对电机各方面的控制。通过对直轴和交轴分量进行解耦,使得交流电机拥有像直流电机一样的控制形式。通过PI电流控制实现对PMSM的基本控制,为之后的控制算法研究提供基础。

2 四轮独立驱动汽车环形耦合控制

2.1 传统环形耦合控制

环形耦合控制是在传统多电机控制的基础上,考虑到任一电机受到扰动都需要整个系统进行调节的问题而建立目标电机与下一个电机之间的联系(末端电机与首个电机建立联系,保证系统形成闭环),以达到任何一个车轮在受到外力的干扰下,其他车轮都可以保持同步的效果[15]。在环形耦合控制中,只有一个速度参考信号,每一个电机在不受到外力干扰的情况下,均与这一参考信号进行比对,以达到跟踪精度的要求。当一个车轮出现扰动时,每一个轮毂电机都与下一个轮毂电机之间建立联系,速度补偿器能保证各轮之间进行转速跟踪,达到相应的同步精度。

环形耦合控制可以保证四轮独立驱动电动汽车在行驶过程中不论一个或者多个车轮受到扰动的情况下,各轮毂电机都可以同步运行。不同于偏差耦合控制,环形耦合控制没有建立目标电机和所有电机之间的联系,而是将各个电机之间的连接形成一个闭环。这种形式大大减少了控制系统的复杂性,提高了控制系统的稳定性。

对于四轮独立驱动形式,采用环形耦合控制方法需要8个控制器。其中4个控制器将电机末端转速信号和目标转速信号进行比对,用于保证各个电机之间的跟踪精度,另外4个控制器将目标电机和下一个电机之间的转速信号进行比对,用于保证各个电机之间的同步精度,控制系统的结构如图1所示。

图1 环形耦合控制原理图

图1中永磁同步轮毂电机采用矢量控制方法,其中,ω*为参考转速信号即给定转速,ω1、ω2、ω3、ω4为轮毂电机末端实时转速,行驶过程中的扰动用给定负载信号的方式代替。

环形耦合控制的速度补偿器结构相比其他速度补偿器较为简单、稳定性更强,是整个控制系统提高跟踪精度的重要部分。该补偿器的工作原理是将目标电机的末端实时转速信号和下一个电机的末端实时转速信号进行比对求差,将速度差值转换为补偿信号补偿给目标电机,从而实现转速的同步。

文献[16]通过李雅普诺夫直接法验证了环形耦合控制的稳定性,系统启动时的同步误差得到控制,可以快速地收敛到零。

2.2 改进型环形耦合控制速度补偿器

传统环形耦合控制的速度补偿器是通过将简单的速度差值补偿信号反馈到控制器中,控制器根据这一信号对电机的速度进行增减以达到各电机之间速度同步的要求。当有电机扰动出现时,速度补偿器反馈到电机上的补偿信号变化较大,同步精度难以得到保证。虽然其结构简单,不需要使用过多的耦合就可以实现既定的控制目标,但控制精度还不够高,直接投入使用会产生一系列问题。

为提高环形耦合控制的控制精度以及各轮之间的同步性能,提出了改进型的环形耦合控制。基于傅里叶级数的学习法[14],将当前速度差值信号与前一个时间单位的速度差值信号同时考虑到本次速度补偿信号中,此时反馈到控制器中的补偿信号不仅可以修正当前电机之间的速度差,还能将前一时间单位的速度差值信号和当前的速度差值信号进行复合运算,传给电机控制器的补偿信号变化曲线相对平滑。当电机速度无规律变化时,仍能保证电机的同步精度。

所提的改进型环形耦合控制方法通过重复运行模式提高控制器的控制性能,降低同步误差以及跟踪误差,速度补偿控制器如图2所示。

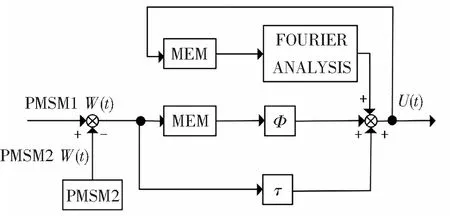
图2 改进型速度补偿器原理图

改进电机系统跟踪精度控制器如图3所示。

图3 改进型跟踪控制器原理图

将电机之间的跟踪误差定义为

ei=ω*-ωi

(3)

式中,ei为电机i的跟踪误差;ω*为给定的初始速度参考值;ωi为电机的转速。

电机i和电机i+1之间的同步误差定义为

εi=ωi-ωi+1

(4)

式中,εi为电机之间的同步误差;ωi为电机i的转速;ωi+1为电机i+1的转速。

则电机i的跟踪误差经过环形耦合控制中的速度补偿模块进行修正,得到

Ei=ei-Kiεi

(5)

式中,Ei为电机i修正后的跟踪误差;Ki为电机的修正系数。

文献[14]的研究表明控制器采用循环学习的方法可以提高控制系统的稳定性, 但其方法只能将跟踪误差限制在一定的范围内,理论值也不能趋近于0。为了进一步增强环形耦合控制系统的控制精度和运行稳定性,结合傅里叶级数的循环学习法提出了一种改进的环形耦合控制方法,控制规律如下

wi+1(t)=FT(wi(t))+Φei(t)+Γei+1(t)

(6)

(7)

式中,wi(t)为控制信号;ei(t)为同步误差信号;Φ为前周期反馈学习增益;Γ为当前周期反馈学习增益。当Γ值过大时会导致误差显著增大,相应的输出控制信号不断放大,整个系统会出现发散的情况,一般选择Γ≤0.8效果较好[14]。

由式(3)、式(4)、式(6)可以得出系统的同步误差以及跟踪误差在傅里叶级数迭代学习下的控制率为

(8)

此时学习增益Φ保持合理的收敛速度才能确保系统的稳定性,由李雅普诺夫稳定性理论可知,系统收敛需要满足如下条件[14]

(9)

式中,P为电机电极数量;ψd为定子磁链;J为电机和负载的总惯量;kt/J大于零。由式(9)可以得出系统的收敛条件如下

(10)

2.3 仿真研究

为验证控制算法是否具有改善同步精度以及跟踪精度的能力,在Matlab/Simulink中搭建模型验证控制算法,通过设定初始值及负载信号的方式模拟汽车在行驶过程中受到的扰动。为了对比本文所提控制方法与其他控制方法的差异,分别搭建偏差耦合控制模型,通过模拟仿真对比分析2种控制方法在实车应用方面的优缺点。具体模拟工况为:参考转速ω*=800 r/min,在0.2 s时对电机2与电机4设置负载信号,用于模拟行驶过程中一侧车轮受到扰动时的情况。在负载信号以及其他条件不变的情况下,传统环形耦合控制和改进型环形耦合控制以及偏差耦合控制的跟踪误差和同步误差如图4～图9所示。

图4 改进前环形耦合控制下各电机的跟踪误差

图5 改进前环形耦合控制下各电机的同步误差

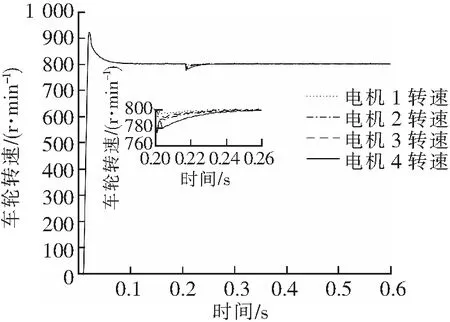
图6 改进后环形耦合控制下各电机的跟踪误差

图7 改进后环形耦合控制下各电机的同步误差

图8 偏差耦合控制中各电机的跟踪误差

图9 偏差耦合控制中各电机的同步误差

图4和图6分别为改进前后各电机之间的跟踪误差。从图4和图6中可以看出,改进前的最高跟踪误差为50 r/min,改进后的跟踪误差均未超过30 r/min,跟踪误差降低61%。图5和图7为分别为改进前后的同步误差。从图5和图7中可以看出,改进前的同步误差最高达到了45 r/min,稳定后的同步误差波动峰值也较高,改进后的最高同步误差最高为25 r/min,同步误差降低46%,稳定后的同步误差峰值较改进前也有所降低。

对比偏差耦合控制方法,环形耦合控制的控制器复杂程度更低,具有更大的改进空间。本文所提改进型环形耦合控制在跟踪精度和同步精度方面都较偏差耦合控制有很大提升,在实车控制中具有一定优势。仿真结果证明,本文所提算法的跟踪精度和同步精度都明显提高,控制性能改善明显。

3 基于CARSIM与Matlab的联合仿真

为进一步的验证改进控制方法在车辆控制中的效果,在Simulink中搭建改进环形耦合控制模型后,基于四轮独立驱动汽车在CARSIM中搭建了实车模型。在CARSIM中选用B型号车作为本次实验的仿真车辆,将其驱动形式调节为四轮驱动并将其驱动源连接Simulink,以Simulink中的4个电机作为B型号车的驱动方式。模拟轮毂电机驱动的电动汽车运行状况,并在后续的研究测试中提供更加接近实车的数据,实验原理如图10所示。

图10 联合仿真原理图

通过CARSIM和Simulink联合仿真模拟工况对改进型环形耦合控制器的性能进行测试。

情景1:路面状况均为常规状态,汽车从0 km/h加速至60 km/h,在行驶至8 s时在汽车前方设置减速带,汽车前轮和后轮相继通过减速带。本工况用于测试汽车加速至给定速度后的超调量及遇到障碍时的恢复能力,控制方法改进前后具体参数图如图11和图12所示。

图11 情景1改进前各轮转速图

图12 情景1改进后各轮转速图

由图11和图12可知,改进环形耦合方法在跟踪精度和同步精度上都比传统环形耦合控制有很大的提升。在加速至给定速度时,改进型环形耦合控制算法的超调量更小,在行驶中车轮在遇到常规扰动时,该算法的同步精度更高而且趋于稳定的速度更快。

情景2:路面状况均为常规状态,汽车以60 km/h的速度行驶,行驶至2 s时在车辆左前方设置一个障碍物体,左前轮以及左后轮先后驶过障碍物。得到改进前和改进后各轮转速如图13和图14所示。

图13 情景2改进前各轮转速图

图14 情景2 改进后各轮转速图

对比图11～图14可知,在车辆行驶过程中四轮同时受到不同干扰的情况下,改进环形耦合控制方法比传统控制方法的稳定性高,具有更优的同步性能和跟踪性能。在受到扰动时可以更快速地恢复至给定速度,同时降低了跟踪误差以及同步误差,汽车在行驶中的安全性大大提高。

4 结论

结合傅里叶级数的学习法对传统的环形耦合控制进行改进,并将其应用到四轮独立驱动电动汽车控制中,协调控制电动汽车的多电机系统。本文提出的改进型环形耦合控制方法,通过在Matlab/Simulink中搭建模型并联合CARSIM进行模拟实况仿真,验证了所提方法的可行性和稳定性。实验表明,本文所提控制方法能够有效地降低电动汽车多电机系统的同步误差和跟踪误差,改善了电动汽车多电机系统的同步性能以及跟踪性能,在不同工况下均可稳定运行,具有一定的实用价值。