基于ICS算法的旅行商问题研究

摘  要：旅行商问题（Traveling Salesman Problem， TSP）是一个NP问题。为了能够获得最优的路径长度以及降低运行时间，文章使用改进的布谷鸟算法（Improved Cuckoo Search， ICS）进行旅行商问题的优化。首先阐述了TSP问题的定义，其次采用布谷鸟算法（Cuckoo Search， CS）进行优化：使用混沌映射进行种群初始化，提高种群多样性；利用量化正交交叉算子对每一次迭代后的个体进行筛选，保证了算法解的质量。仿真实验中与ACO、PSO和CS对比，该文算法在TSP的最优路径和最短时间方面具有一定的效果。

关键词：TSP；混沌；正交交叉

中图分类号：TP18  文献标识码：A  文章编号：2096-4706（2023）13-0092-04

Research on Traveling Salesman Problem Based on ICS Algorithm

QUAN Yu

（Science Technology Bureau of Shaoxing， Shaoxing  312000， China）

Abstract： Traveling Salesman Problem （TSP） is a NP problem. In order to obtain the optimal path length and reduce running time， this paper uses the improved Cuckoo search （ICS） algorithm to optimize the traveling salesman problem. Firstly， the definition of the TSP problem is explained， and then the Cuckoo search （CS） algorithm is used for optimization： chaos mapping is used for population initialization to improve population diversity; the quantization orthogonal crossover operator is used to screen the individuals after each iteration， ensuring the quality of the algorithm solution. Compared with ACO， PSO， and CS in simulation experiments， the proposed algorithm in this paper has certain effectiveness in terms of optimal path and shortest time of TSP.

Keywords： TSP; chaos; orthogonal crossover

0  引  言

旅行商問题是一个经典的线路优化问题，如何最大程度减少TSP的时间、提高优化效率是当前学者们研究的主要方向。文献[1]提出一种基于大规模邻域搜索的模拟退火算法解决旅行商问题，仿真结果表明所提方法收敛效果好和鲁棒性强，能够有效求解旅行商问题；文献[2]针对TSP问题，提出一种新的ACAG算法，实验结果表明该算法性能明显优于传统的蚁群算法和遗传算法，降低了TSP问题的求解时间；文献[3]针对TSP问题提出一种优化的量子蚁群算法，在求解旅行商问题时，提出的算法在最优值差别不大的情况下，减少了早熟，大幅度提高了算法的收敛速度；文献[4]在TSP问题中提出一种带遗忘因子的蚁群优化算法，在TSP实例的仿真结果表明能够耗时更短，路径寻优结果更优；文献[5]提出了一种改进的混合遗传蚁群算法，仿真结果表明该算法在求解不同规模的旅行商问题时具有更强的全局搜索性及快速收敛性。文献[6]在TSP问题中提出改进离散蝴蝶优化算法，该算法为了提升搜索效率，利用贪婪机制初始化种群，同时结合2-OPT算子、改进的2-OPT算子和模拟退火等策略来提高寻优能力，仿真结果表明提出的算法在寻优能力和鲁棒性方面表现优越；文献[7]利用深度强化学习模型SAC对遗传算法进行改进，并将其应用至旅行商问题（TSP）的求解，通过对TSPLIB实例的实验结果表明改进的遗传算法可有效地避免陷入局部最优解，在提高种群收敛速度的同时，减少寻优过程的迭代次数；文献[8]借鉴对抗学习的思想解决旅行商问题，核心思想是使用监督学习的方式来产生对抗样本，并将对抗样本加入随机样本中混合训练，以改善模型对该类问题的泛化性能，仿真实现验证了所提出方法的有效性；文献[9]在解决TSP问题中设计了一种随机最佳插入的烟花算法（RBIFWA），仿真表明RBIFWA算法在求解TSP问题上具有更加优秀的性能和更高的求解质量。

在以上的研究成果中发现大部分解决TSP问题的方法都是采用了元启发式的智能算法，从实验结果看获得了较好的效果，本文将继续这一思想的指导下进行研究，将ICS算法用于解决TSP问题。首先阐述了TSP问题基本概念，其次针对CS算法使用混沌映射进行种群初始化，提高种群多样性，利用量化正交交叉算子对每一次迭代后的个体进行筛选，保证了算法的解的质量，通过仿真实验说明该算法具有较好的效果。

1  旅行商问题简介

求解TSP问题的本质是求解一个NP完全问题，由于TSP问题涉及的范围越来越广，使得计算规模逐渐增大，从而导致规划路径中所需要的计算量呈现指数级的改变。而TSP问题的本质就是在具有n个顶点组成的无向闭合回路的完全图G =（V，E，r）中利用最小的时间和最低的成本遍历完成所有的顶点的边之和。假设顶点集合V = {1，2，…，n}中每一个点表示需要访问的城市，E表示这些顶点中的不同顶点组成的边集，r设定为每一边的权值。因TSP问题的数学模型表达如下：

以上公式中，式（1）表示求解TSP的目标函数，其中xi，j表示两个城市，di，j表示2个城市之间的权重值。式（2）（3）表示旅行者只能走过一个城市，式（4）表示旅行商走过的任何城市中子集中不能形成循环。

2  基本CS算法简述

布谷鸟算法（Cuckoo Search， CS）是一种元启发式的算法。该算法模拟布谷鸟的巢寄生行为和Levy行为。具体算法描述如下：

1）算法随机产生N个鸟窝的位置表达为 ，任意选择其中一个最佳的鸟窝传递给下一代。

2）算法的位置更新主要依靠Levy飞行进行迭代，将新获得鸟窝中下一代个体位置对比上一代的鸟窝位置，从中寻找位置最好的个体。

3）将随机数r ∈ [0，1]对比宿主鸟发现外来鸟蛋概率Pa。当r＞Pa，则将该鸟窝的位置进行改变，否则不变，然后对比上一代鸟窝的位置，从中选择出位置更好的鸟窝即 。

4）计算获得最新的鸟窝位置是否达到精度或者迭代条件，则该鸟窝为算法的全局最优解，否则继续转2）执行。

布谷鸟算法中每一个巢中的卵代表算法的解，表达式如下：

式中， 表示第t代中的第i个鸟窝位置；?表示点对点乘法，α表示步长，L（λ）表示随机搜索路径。

3  ICS算法的旅行商问题优化

从旅行商问题的求解中发现，该问题是一个典型的NP问题，而采用元启发式算法是求解该问题关键。本文采用CS算法进行求解旅行社问题。CS算法凭借实现原理简单，容易操作等优点而被广泛地进行应用，但是它像大部分元启发式算法一样存在陷入局部最优，收敛速度慢等缺点。本文从种群初始化和个体筛选两个方面对算法进行优化，一方面使用混沌对种群进行初始化提高多样性，另一方面通过正交交叉算子进行个体筛选，提高解的质量。

3.1  种群初始化

CS算法的种群个体初始值仅仅通过随机方式处理，这样容易使得算法在后期陷入局部收敛，解的多样性受到严重影响。而混沌思想具有随机性，遍历性等优点，它能够保证算法解获得多样性。它的主要思想是将解的个体映射关系某个区间中，从而产生混沌解，然后对应到个体的搜索空间中，提高了种群的解的多样性。本文采用的混沌表达式为：

式中，xi表示布谷鸟个体，xi+1表示混沌后的布谷鸟个体。rand（0，1）表示0和1之间的随机函数。我们将混沌后的布谷鸟个体和原始个体进行适应度比较，选择两者中最优的个体组成初始化种群。

3.2  个体筛选

CS算法在每一次迭代后没有对个体进行筛选，这样就容易造成质量差的个体也进入了下一次迭代，从而降低了解的质量，为了避免这种情况的发生，同时提高解的效率，本文提出使用量化正交交叉算子用于个体筛选和提高个体解质量。过程阐述如下：

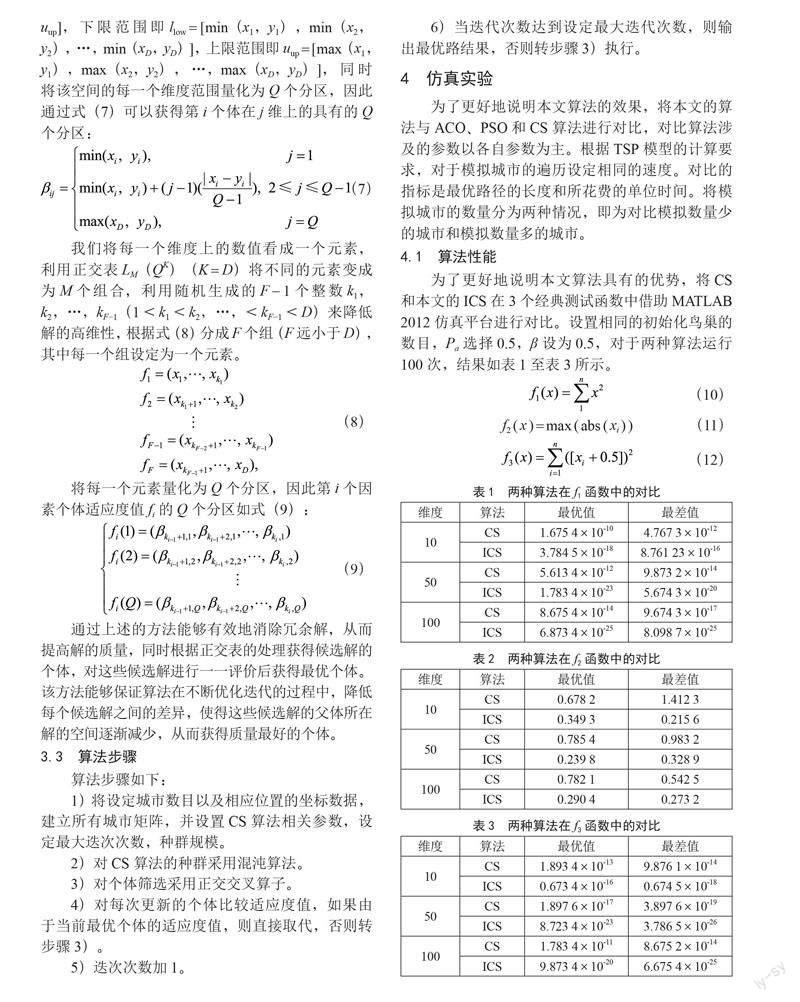
我们先假设x =（x1，x2，…，xD）和y =（y1，y2，…，yD）分别表示不同两个父体的候选解，我们将这两个候选解定义在同一个搜索空间中[llow，uup]，下限范围即llow = [min（x1，y1），min（x2，y2），…，min（xD，yD）]，上限范围即uup = [max（x1，y1），max（x2，y2），…，max（xD，yD）]，同时将该空间的每一个维度范围量化为Q个分区，因此通过式（7）可以获得第i个体在j维上的具有的Q个分区：

我们将每一个维度上的数值看成一个元素，利用正交表LM（QK）（K = D）将不同的元素变成为M个组合，利用随机生成的F - 1个整数k1，k2，…，kF-1（1＜k1＜k2，…，＜kF-1＜D）来降低解的高维性，根据式（8）分成F个组（F远小于D），其中每一个组设定为一个元素。

将每一个元素量化为Q个分区，因此第i个因素个体适应度值fi的Q个分区如式（9）：

通过上述的方法能够有效地消除冗余解，从而提高解的质量，同时根据正交表的处理获得候选解的个体，对这些候选解进行一一评价后获得最优个体。该方法能够保证算法在不断优化迭代的过程中，降低每个候选解之间的差异，使得这些候选解的父体所在解的空间逐渐减少，从而获得质量最好的个体。

3.3  算法步骤

算法步骤如下：

1）将设定城市数目以及相应位置的坐标数据，建立所有城市矩阵，并设置CS算法相关参数，设定最大迭次次数，种群规模。

2）对CS算法的种群采用混沌算法。

3）对个体筛选采用正交交叉算子。

4）对每次更新的个体比较适应度值，如果由于当前最优个体的适应度值，则直接取代，否则转步骤3）。

5）迭次次数加1。

6）当迭代次数达到设定最大迭代次数，则输出最优路结果，否则转步骤3）执行。

4  仿真实验

为了更好地说明本文算法的效果，将本文的算法与ACO、PSO和CS算法进行对比，对比算法涉及的参数以各自参数为主。根据TSP模型的计算要求，对于模拟城市的遍历设定相同的速度。对比的指标是最优路径的长度和所花费的单位时间。将模拟城市的数量分为两种情况，即为对比模拟数量少的城市和模拟数量多的城市。

4.1  算法性能

为了更好地说明本文算法具有的优势，将CS和本文的ICS在3个经典测试函数中借助MATLAB 2012仿真平台进行对比。设置相同的初始化鸟巢的数目，Pa选择0.5，β设为0.5，对于两种算法运行100次，结果如表1至表3所示。

4.2  TSP问题效果对比

构建5个模拟城市的坐標分别是（13，13）、（17，35）、（20，20）、（35，15）、（30，40），分布如图1所示。图2和图3分别展示了4种算法的在城市中的最优路径的长度和所花费的单位时间。从图2中发现4种算法在城市最优路径长度比较方面相差不大，虽然本文算法相比于其他算法具有一定的优势，但是这种优势并不是十分明显，这主要是由于模拟城市的数量较少，算法的性能可能好没有得到充分的体现。从图3中发现4种算法在寻找最优路径时候的花费时间的对比，从图中发现4种算法所消耗的单位时间都比较少，这主要是由于模拟城市数量较少的原因，但是总体上本文算法的时间具有一定的优势，这主要是因为本文算法在种群初始化，位置更新和个体筛选方面进行了优化，使得算法的性能得到了提升，因此降低了算法的运行时间。

5  结  论

针对TSP问题中的路径和运行时间长的问题，本文提出了一种改进的CS算法，它使用混沌映射进行种群初始化，提高了种群多样性，并利用量化正交交叉算子对每一次迭代后的个体进行筛选，保证了算法的解的质量，仿真实验中在模拟城市数量少和多的情况下，本文算法相比于ACO、PSO和CS都具有较好的效果

参考文献：

[1] 孙鉴，刘凇佐，武晓晓.基于大规模邻域搜索的模拟退火算法求解TSP [J/OL].计算机仿真，（2023-01-02）[2023-01-23].https：//www.cnki.net/KCMS/detail/detail.aspx？dbcode=CAPJ&dbname=CAPJLAST&filename=JSJZ20221229002&v=MTQ2MDRyWTFNWk9zTll3azd2QkFTNmpoNFRBemxxMkEwZkxUN1I3cWRaT1pwRmlIbFZiM0JKVjg9THo3QmRMRzRITlBO.

[2] 圣文顺，徐爱萍，徐刘晶.基于蚁群算法与遗传算法的TSP路径规划仿真 [J].计算机仿真，2022，39（12）：398-402+412.

[3] 李想，董玉民.一种优化的量子蚁群算法在旅行商问题上的应用 [J].重庆师范大学学报：自然科学版，2022，39（5）：127-133.

[4] 赵鑫，杨雄飞，钱育蓉.改进的蚁群优化算法求解旅行商问题 [J].计算机工程与设计，2022，43（4）：962-968.

[5] 郑娟毅，程秀琦，付姣姣.改进蚁群算法在TSP中的应用研究 [J].计算机仿真，2021，38（5）：126-130+167.

[6] 谢聪.求解TSP问题的改进离散蝴蝶优化算法 [J].数学的实践与认识，2020，50（1）：173-182.

[7] 陈斌，刘卫国.基于SAC模型的改进遗传算法求解TSP问题 [J].计算机科学与探索，2021，15（9）：1680-1693.

[8] 熊文瑞，陶继平.自适应对抗学习求解旅行商问题 [J].计算机工程与应用，2022，58（17）：224-229.

[9] 吴俊斌，吴晟，吴兴蛟.一種用于求解TSP问题的随机最佳插入烟花算法 [J].计算机工程与科学，2020，42（11）：2080-2087.

作者简介：全瑜（1985.01—），男，汉族，浙江绍兴人，工程师，本科，研究方向：信息技术。

收稿日期：2023-02-27