一种对抗雷达组网的干扰目标分配方法
陈思南
(中国电子科技集团公司第二十九研究所,四川成都 610036)
0 引 言
近年来,随着电子对抗技术的迅猛发展,为了在复杂电子干扰的战场环境下有效探测突防飞机,预警探测体系已经由传统的单基地雷达探测转变为雷达组网系统协同探测[1-2]。雷达组网通过系统内部信息共享的方式,相比于单雷达的探测更为有效,已经对我方突防编队构成巨大威胁。为了提高我方突防飞机的生存概率和突防任务的成功率,需要运用协同干扰的模式对抗敌方雷达组网[3-4]。在干扰装备资源有限的情况下,通过制定合理的干扰目标分配方案,从而实现协同干扰效果的最大化,以达到对抗雷达组网的最佳效果[5]。
针对干扰目标分配问题,文献[6-7]通过对目标特征、对抗能力和飞机位置变化信息的分析,解决了一对一的干扰目标分配决策问题。文献[8-9]基于遗传算法和蚁群算法,解决了单部干扰装备可同时对抗多部雷达情况下的干扰目标分配问题。文献[10-12]通过对目标威胁程度和干扰效益等问题的分析,运用贪心算法、粒子群算法和遗传算法,解决了多部干扰装备可同时对抗单部雷达的干扰目标分配问题。然而在现代电子战的复杂电子对抗环境下,电子干扰系统对抗雷达组网系统,往往是单部干扰装备可同时干扰多个雷达目标,并且单个雷达目标也会同时被多部干扰装备干扰。此外,不同干扰装备之间的干扰能力也存在一定的差异性。
针对上述问题,本文以掩护我方突防飞机,多干扰装备协同对抗雷达组网为作战场景,基于雷达组网探测概率,考虑干扰资源有限和干扰效果叠加的约束,构建了多对多的干扰目标分配模型。对传统遗传算法进行了优化,提高了算法的收敛效率和寻优概率。利用改进的遗传算法对本文构建的干扰目标分配模型求解,通过计算机仿真验证了模型和算法的有效性。
1 干扰目标分配模型
1.1 数学模型
假设我方有M部不同种类的干扰装备,需要对N个敌方雷达目标组成的预警探测雷达网实施协同干扰。我方干扰装备最多可以干扰雷达目标的数量用向量L表示,单个雷达目标在没有被干扰的情况下对我方突防飞机的探测概率用向量P表示。单部干扰装备对单个雷达目标的干扰效果系数用矩阵U表示。干扰效果系数表示单个雷达目标被单部干扰装备干扰后的探测概率损失率。
li表示第i(i=1,2,…,M)部干扰装备可干扰的雷达目标数量,该数值小于N;pj表示第j(j=1,2,…,N)个雷达目标在没有被干扰的情况下对我方突防飞机的探测概率;uij表示第i部干扰装备对第j个雷达目标的干扰效果系数。
为了降低模型的复杂度,通过对每部干扰装备分解成多部“虚拟”干扰装备的操作,将多对多的分配问题转化为一定约束条件下的一对多的分配问题。“虚拟”干扰装备的数量即为每部干扰装备最多可干扰雷达目标的数量,例如:把第i部干扰装备分解成li部“虚拟”干扰装备。再对分解之后得到的所有“虚拟”干扰装备重新编号,例如:第1 部到第l1部“虚拟”干扰装备对应第1 部干扰装备,第l1+1 部到第l1+l2部“虚拟”干扰装备对应第2部干扰装备,以此类推最终可以得到共计M′部“虚拟”干扰装备。
干扰分配结果由矩阵X′表示,xi′j表示第i′(i′=1,2,…,M′)部“虚拟”干扰装备对第j个雷达目标的分配结果,xi′j= 1 则表示第i′部“虚拟”干扰装备对第j部雷达目标实施干扰;xi′j= 0则表示不干扰[13]。单部“虚拟”干扰装备对单个雷达目标的干扰效果系数用矩阵U′表示,u′i′j表示第i′部“虚拟”干扰装备对第j个雷达目标的干扰效果系数。
每部干扰装备携带多套独立的干扰资源,所以每部干扰装备对应的“虚拟”干扰装备对同一个雷达目标的干扰效果系数相同,即为该部干扰装备对该雷达的干扰效果系数,例如:第1 部干扰装备对应的l1部“虚拟”干扰装备对第j个目标雷达的干扰效果系数u′1j=u′2j= … =u′l1j=u1j。
1.2 目标函数
组网雷达中每个雷达对我方突防飞机都有一定的探测概率,同时组网雷达之间会通过网络进行信息共享,提高整个雷达组网系统的探测概率。雷达组网系统对我方突防飞机的探测概率[14]表示如下:
多部干扰装备协同干扰一个雷达目标时,协同干扰效果会在单部干扰装备分别干扰单个雷达目标的基础上叠加。干扰目标分配模型的目标函数,即雷达组网系统被多部干扰装备协同干扰后的探测概率表示如下:
1.3 约束条件
考虑到实际作战环境下单部干扰装备的干扰效果、干扰资源有限以及干扰装备的干扰状态等因素,建立干扰目标分配模型的约束条件如下:
式(9)表示每部“虚拟”干扰装备最多只能干扰一个雷达目标,以保证给每部干扰装备分配的雷达目标数量不会超过该干扰装备可以干扰雷达目标数量的上限;式(10)表示每部干扰装备的第一部“虚拟”干扰装备的编号,例如:ki表示第i部干扰装备的第一部“虚拟”干扰装备的编号;式(11)表示每部雷达目标不会被重复分给同一部干扰装备多次,以免干扰资源的浪费;式(12)表示每部“虚拟”干扰装备对每个雷达目标只有干扰和不干扰两个状态。
综上所述,干扰目标分配的过程就是要在满足式(9)~(12)的约束条件下,找到一个干扰目标分配方案,使得雷达组网系统的探测概率最小[15]。
2 改进的遗传算法
遗传算法是通过模拟生物进化的遗传规律和自然选择机理的一种搜索最优值的方法,通过不断地种群繁衍进化,最终得到适应能力强的个体[16-17]。经典的遗传算法有时会需要较长的迭代过程才能得到最优解,并且有可能收敛于局部最优而不是全局最优。通过对干扰目标分配模型的分析,本文主要对遗传算法中的个体编码方式、适应度函数计算、种群的初始化、交叉操作、变异操作、最优解的选取等环节进行了优化;复制操作选取的是经典的轮盘赌选择法。改进的遗传算法流程如图1所示。
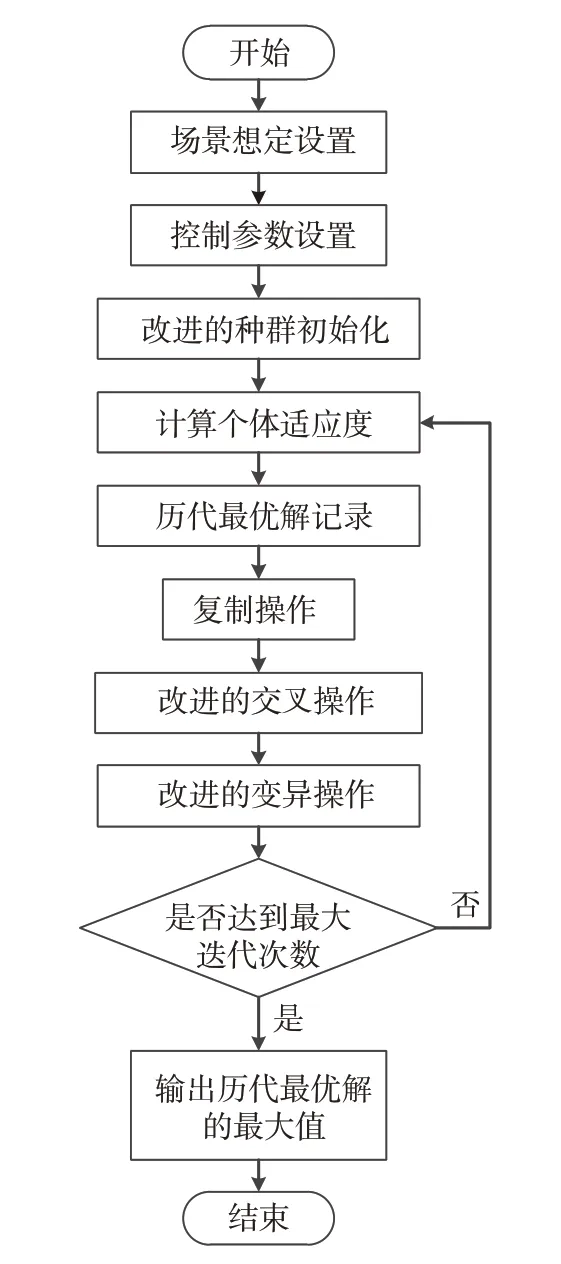
图1 改进的遗传算法流程图
2.1 编码方式选择
传统的二进制编码方式会导致染色体长度过长,算法的计算量过大。为了提高算法的时效性,本文采取十进制的编码方式构建染色体。将染色体长度设置为“虚拟”干扰设备的总部数M′;每个基因的值表示对应的雷达目标编号,例如:染色体第1个基因值为5,表示第1部干扰装备对应的第1部“虚拟”干扰装备对5号雷达目标实施干扰。
2.2 适应度函数优化
干扰目标分配就是要充分利用已有的干扰资源,在一定的约束条件下,对雷达组网产生的协同干扰效果的最大化。根据式(8)将适应度函数设置如下:
为了充分利用干扰资源,以取得最佳的干扰效果,基因的取值范围限定在自然数1~N之间,即每部“虚拟”干扰装备都会被分配一个目标雷达,从而满足了式(9)和式(12)的约束条件。由于编码方式由二进制改为十进制,式(11)的约束条件优化如下:
yn表示给第n部“虚拟”干扰装备分配的雷达目标编号;li≥2 表示仅计算最大可干扰2 个及以上的雷达目标的干扰装备,仅能干扰1个雷达目标的干扰装备一定满足式(11)的约束条件,因此无需再次验证该约束条件。对于不满足约束条件的个体引入惩罚机制,令该个体的适应度值为0。
2.3 改进的种群初始化
一般情况下初始种群的设定是随机的,随机产生的个体很难满足本文模型的约束条件,容易产生很多“无效”个体,从而减缓算法的收敛速度;但是过度人为干预而产生的初始种群往往又不具有多样性。所以本文初始种群的选择采用在一定条件下随机生成的方式,即按照干扰装备的顺序依次随机生成目标分配结果,最后将所有干扰装备的目标分配结果组合而成一个随机个体。具体做法是在N个雷达目标中随机选取li个分配给第i部干扰装备,待每部干扰装备所干扰的目标分配结束后,再将M′个分配结果按照“虚拟”干扰装备编号规则重新排列就生成了一个随机个体。
2.4 改进的交叉操作
经典的交叉操作的是随机的单点交叉,并且每次交叉的位置都是随机在染色体中的任何位置。根据式(14)的约束条件可知,这种交叉操作生成“无效”个体的概率较大,从而降低算法的收敛速度。本文采用的交叉操作如图2所示。

图2 改进的交叉操作示意图
首先将染色体按照干扰装备的数量分成M个“子染色体”,“子染色体”的个数即为交叉点的个数。接着对每个“子染色体”内的基因按照升序重新排列。然后单独计算每个“子染色体”的交叉概率;并且每个交叉点的具体位置是在“子染色体”内部随机选取,最后的交叉操作在每个“子染色体”内部的基因之间进行的。改进的交叉操作可以很大程度地减小产生不满足约束条件的“无效”个体的产生,提高了种群的多样性和算法的收敛速度。
2.5 改进的变异操作
在最初几代种群中,个体之间的差异较大,应采用较低的变异概率满足收敛的快速性。随着种群的进化,个体间的多样性明显下降[18]。此时就要随之调整染色体的变异概率,防止陷入局部最优,本文设计的动态变异概率表示为
式中Qmax表示最大变异概率,Qmin表示最小变异概率,V表示当前种群中每个个体适应度的标准差,Vmax表示历代种群中个体适应度标准差的最大值。为了使动态变异概率有效地发挥作用,需要在计算个体适应度标准差时,事先剔除适应度为0 的个体。
2.6 改进的最优解选取方式
进化过程中的交叉和变异会有一定概率导致适应度值大的个体被淘汰,引入动态变异概率后,进一步提高了适应度值大的个体被淘汰的概率。而这些被淘汰的历史局部最优解中有可能就是全局最优,为了防止“错过”全局最优,需要记录每代种群中适应度最高的个体。待进化结束后在历史局部最优解中选取最大值作为算法的最终结果。
3 仿真验证
3.1 实例分析
作战场景想定:假设我方出动3部干扰装备掩护突防飞机,需要对抗敌方某区域内7个雷达目标组成的雷达组网系统。每部干扰装备最大可干扰雷达目标的数量如表1 所示,即第1 部干扰装备最多可以干扰2 个雷达目标;第2 部干扰装备最多可以干扰3 个雷达目标;第3 部干扰装备最多可以干扰4个雷达目标。

表1 干扰装备可干扰雷达目标的数量
每部雷达目标的探测概率如表2所示,每部干扰装备对每个雷达目标的干扰效果系数如表3所示。

表2 雷达目标的探测概率
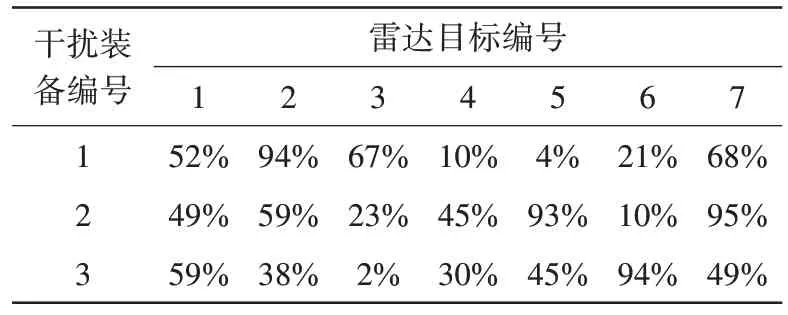
表3 干扰效果系数
遗传算法的群体规模设置为200,最大遗传进化代数设置为100,交叉概率设置为85%,最大变异概率设置为10%,最小变异概率设置为1%。带入相关控制参数,经过计算机仿真,得到个体最大适应度值为0.627 4,干扰目标分配结果如表4 所示,即第1 部干扰装备干扰第2、3 个雷达目标;第2部干扰装备干扰第1、4、7 个雷达目标;第3 部干扰装备干扰第1、4、5、6个雷达目标。
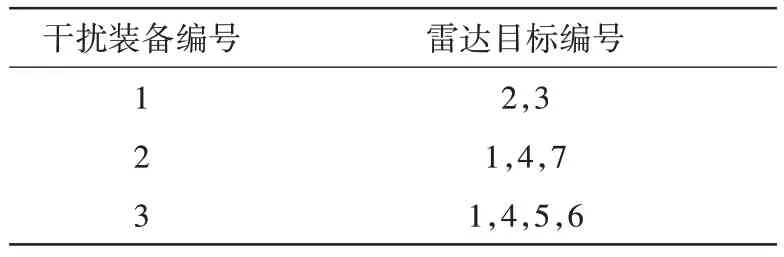
表4 干扰目标分配结果
根据式(8)计算雷达组网系统被干扰装备协同干扰压制后的探测概率为37.26%,根据式(7)计算协同干扰前雷达组网探测系统的探测概率为99.05%。从中可以看出基于目标分配的协同干扰明显降低了雷达组网系统的探测概率,有效地掩护了我方突防飞机。
3.2 算法比较
对改进前后的遗传算法分别进行100 次蒙特卡洛仿真,改进后的遗传算法和改进前的遗传算法得到的目标函数值对比如图3所示。
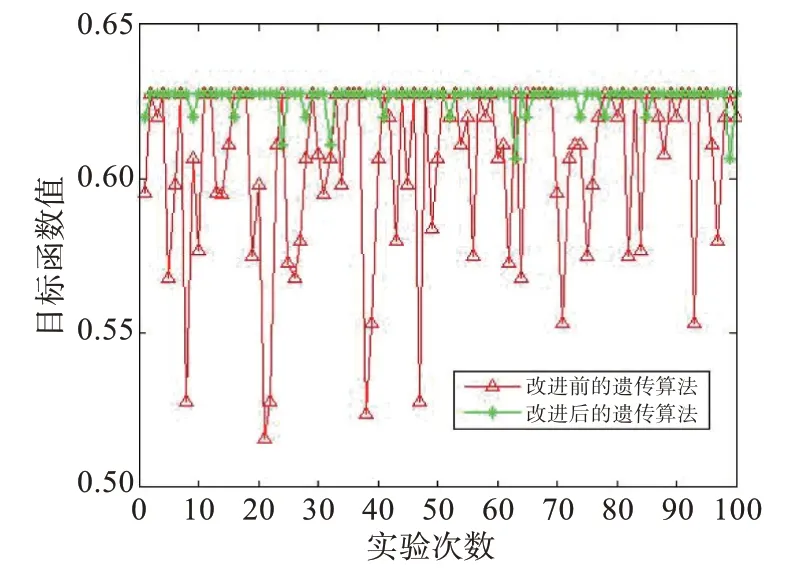
图3 目标函数值对比
改进后的遗传算法和改进前的遗传算法搜索到全局最优解的概率分别是86%和40%;搜索到全局最优解或次优解的概率分别是96%和51%;第一次搜索到最优解时的平均进化代数分别是42代和63代。改进后的遗传算法和改进前的遗传算法的历次蒙特卡洛实验最优解的最小值分别为0.606 7 和0.516 0;平均最优解分别为0.625 9 和0.605 3。可见改进后的遗传算法相比于改进前在时效性和鲁棒性方面得到了明显的改善。
4 结束语
针对现代电子战争中对抗多雷达组网的干扰目标分配问题,本文提出了一种基于雷达目标探测概率和干扰装备干扰效果系数的多对多的目标分配模型,并根据实战环境建立了目标分配模型的约束条件。采用了遗传算法对问题模型进行求解,为了降低算法的复杂度,改进了编码方式和适应度函数;为了提升算法的收敛速度,改进了种群初始化方式和交叉操作;为了防止算法陷入局部最优,改进了变异操作和最优解的选取方式。本文的方法保证了干扰装备协同压制多雷达组网系统的作战效能,实时性和有效性也得到了验证。下一阶段将针对动态作战过程以及更为复杂的雷达组网模式下的干扰目标分配建模开展进一步的研究。

