基于改进PFA的车载大斜视SAR成像算法
王佳慧,刘衍琦,王纪平,金 秋,毛新华
(南京航空航天大学电子信息工程学院雷达成像与微波光子技术教育部重点实验室,江苏南京 211106)
0 引 言
随着智能驾驶辅助系统(Advanced Driver Assistance System,ADAS)的兴起,车载毫米波雷达在保障驾驶员和乘客的安全性上起到不可替代的作用。车载毫米波雷达通过接收回波信号感知周围环境,是实现自适应巡航控制、自动紧急刹车等功能必不可少的传感器[1]。与摄像头相比,毫米波雷达不受环境限制,在雨雪等复杂环境下也可发挥作用。低成本、高可靠性的特点使得毫米波雷达更胜一筹。基于以上优势,再加之技术趋于成熟,毫米波雷达已被装载到越来越多的汽车上投入使用[2]。
实际应用中为了保证行车安全,不仅要对正侧方场景进行观察,同时要将天线倾斜以方便对斜视方向的情况进行探测。雷达斜视时,距离向与方位向两维耦合严重,距离多普勒算法(Range Doppler Algorithm, RDA)存在近似,斜视会使误差变大,成像困难。后向投影算法(Back-Projection Algorithm,BPA)适应于斜视情况,但是考虑到车载环境下对算法的实时性要求很高,而BPA 计算复杂,效率低,也难以应用。与之相比,PFA在时域进行运动补偿,适应于非线性航迹,且成像实时性好,因此得到广泛应用。但其只适应于小场景下的聚束数据的处理,因此在车载环境下需要做出改进。
市场的扩大和用户需求量的增加对车载雷达提出了更高的要求,因此车载毫米波雷达成像已经得到了社会各界研究者的广泛关注。将多传感器融合技术用于车载SAR 系统是一种比较先进的方式,但是该方法高度依赖于惯导信息,成本较高[3]。有关正侧视的车载毫米波雷达成像研究较多,也都获得了较好的结果和应用,比如短距情况下的人体和车辆检测等[4-6]。BPA 适应于斜视,因此关于车载毫米波雷达斜视成像的处理应用BPA较多,但是考虑到实时性则需要做出进一步的研究[7-8]。
为了解决当前车载环境下斜视成像困难的问题,在综合分析现有各种雷达成像算法特点的前提下,本文提出了一种改进的极坐标格式算法,将全孔径条带SAR 回波划分为子孔径,对子孔径数据进行PFA 处理和几何失真校正,将子图像进行截取、拼接得到条带SAR 成像结果。同时,一定条件下以重叠子孔径的方式划分全孔径保证成像的高分辨率。通过用所提算法对点目标和实测数据进行仿真处理,目标均成像在正确的位置上,并得到了完整的高分辨率图像。
1 基于子孔径拼接的极坐标格式成像算法
1.1 子孔径划分
车载毫米波雷达以条带模式采集数据,其特点是天线指向不变,波束照射区域与雷达同向运动,能够获取较大场景的回波。聚束模式下天线波束指向时刻变化,波束照射区域固定,获取数据的场景较小。PFA适用于小场景下的聚束模式,原因如下:一是PFA 存在平面波假设,存在几何失真,且场景越大误差越大,而通常车载环境的场景较近,波前弯曲误差更加严重;二是PFA 以场景中心作为参考点进行运动补偿,距离中心点越远误差越大。为了使用PFA 处理条带数据,需要先将条带数据转换为聚束数据。转换示意图如图1 所示,车辆从Q行驶到Q′的过程中,对应长度为Lg的阴影部分始终处于波束照射下,符合聚束数据的特点。条带合成孔径长度为L,等效聚束合成孔径长度为Ls,斜视角为θs。当车辆行驶速度也即雷达运动的速度为Vr,子孔径回波个数为Naa时,Ls=VrNaa/PRF,要求L>Ls。由于毫米波雷达波束较宽,对其进行滤波后得到方位向波束宽度为β。

图1 条带数据转换为聚束数据的几何模型
子孔径脉冲个数Naa的选择首先要满足相邻子孔径间无间隔,其次为了使成像结果看起来无拉伸感,应使距离向与方位向分辨率相匹配。
1.2 子孔径数据的极坐标格式算法处理
毫米波雷达发射线性调频连续波(Linear Frequency Modulation Continuous Wave, LFMCW)信号为
式中A表示信号幅度,kr为距离向线性调频斜率,fc为信号载频,tr表示距离向快时间变量,ta表示方位向慢时间变量,Tr为脉冲宽度,Ta为目标在波束下的照射时间。
忽略信号传输过程中的幅度变化,设回波延迟为τ0,则经过解调后天线接收到的回波信号为
毫米波雷达带宽较大,达到几个GHz,同时在车辆行驶过程中,探测场景相对较小,为了降低带宽、简化AD 采样、降低硬件要求,车载毫米波雷达通过在模拟阶段使用Dechirp 的方式进行脉冲压缩,脉冲压缩后的表达式为
将式(3)进行距离向FFT,得到
式中fr为距离频率,sinc 函数的峰值位于fr=krτ0处,经过残余视频相位去除(RVP)后,得到
忽略俯仰角,图2为车载毫米波雷达子孔径在斜视情况下采集数据的几何模型,以场景中心O为坐标原点,平行于雷达运动方向为X轴,垂直于雷达运动方向为Y轴建立坐标系。图中P(xt,yt)为目标位置,θs为斜视角,Rt和Ra分别为雷达天线相位中心到目标和场景中心的距离,雷达方位角为θ,雷达航迹到X轴的距离为y0。
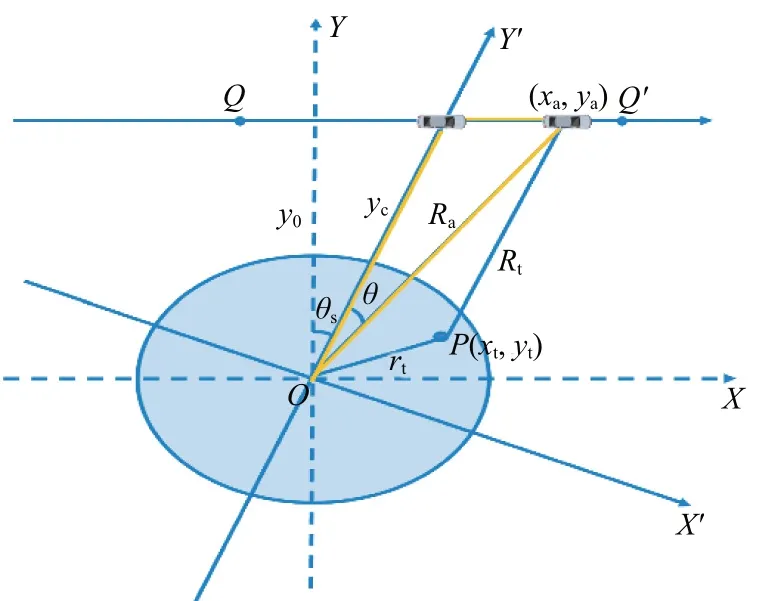
图2 子孔径采集数据的几何模型
将式(5)作距离向IFFT并忽略幅度得到
对每一个子孔径的场景中心单独做运动补偿后
式中RΔ=Rt-Ra为雷达天线相位中心到目标与场景中心的距离差。
在平面波假设条件下
则波数域的信号表示为
式中,
由式(9)及式(10)可知,进行两维FFT 后即可得到成像结果,但雷达信号在波数域是以极坐标格式进行的非均匀采样,需要先经过距离向和方位向插值实现两维均匀重采样后才能通过两维FFT实现聚焦。
1.3 几何失真校正
在平面波条件下用式(8)近似,但雷达波前为球面波,所以平面波近似会带来波前弯曲误差。随着对分辨率要求的提高、成像场景的扩大和成像距离的减小,波前弯曲误差愈加不可忽略[9]。将式(9)进行两维Taylor展开得到
式中Kyc=4πfc/c为Ky的偏置,c表示电磁波在空气中的传播速度。
在图2 中,建立了XOY平面直角坐标系,对其进行旋转得到新的坐标系X′OY′,旋转角度为θs,雷达位置为(xa,ya),孔径中心时刻雷达到X′轴的距离为yc。坐标旋转如下:
为了得到Taylor 展开式的系数,用θ表示所有项,在图2中有
同时在橙色三角形中Vrta/sinθ=yc/cos(θs+θ),得到
将式(13)和式(14)代入式(10)得到相应的系数为
至此完成了子孔径数据的PFA 处理及其几何失真校正,步骤如图3所示。

图3 子孔径成像及几何失真校正过程
1.4 子孔径图像拼接
由上述分析可知,子孔径回波个数的选择取决于波束宽度和分辨率[12]。将子孔径回波数据利用PFA 成像并进行几何失真校正后得到子图像,需要按照顺序将子图像拼接起来得到全部区域的成像。
子孔径的划分与拼接详细介绍如下。如图4(a)所示。l2与l3之间为实际成像需要的部分。当Ls≤Le时,直接截取对应的虚线框内的成像场景部分进行拼接,拼接示意图如图4(b)所示,其中W1=Ls/ρx,对应的是雷达也即车辆在子孔径数据时间内运动的距离,ρx为坐标系内相邻点的横向方位间隔。


图4 Ls ≤Le时子孔径划分与拼接示意图
当Ls>Le时,为了在实现连续拼接的同时保证分辨率,采用重叠子孔径的方法[13]。重叠子孔径的划分方式如图5(a)所示,第一个子孔径为Q1Q′1,第二个子孔径为Q2Q′2,其回波个数为Naa,长度为Ls=VrNaa/PRF。设置两个子孔径间重叠的回波个数为N′aa,则对应的长度为Lc=VrN′aa/PRF,那么相邻两个子孔径间的重叠率rate=N′aa/Naa=Lc/Ls。子孔径拼接如图5(b)所示,其中W2=(Ls-Lc)/ρx,对应的是未重叠部分雷达运动的距离。
设全孔径回波信号个数为Na,由上述分析可知,当子孔径无重叠时,划分的子孔个数为K1=Na/Naa。当子孔径重叠时,划分的子孔径个数为,式中数学符号代表向上取整。基于子孔径拼接的条带车载毫米波雷达斜视SAR全孔径成像流程如图6所示。

图5 Ls >Le时重叠子孔径划分与拼接示意图
成像效率也是车载环境中需要考虑的重要因素。利用文献[14]的方法进行成像复杂度的计算如表1 所示,计算复杂度主要来自于成像过程中的复乘运算,其中M′为全孔径回波脉冲个数,M为一个子孔径中的脉冲个数,K为划分的子孔径数,N为每个脉冲的采样点数。

表1 计算复杂度
2 仿真和实测数据处理
2.1 点目标仿真
为了验证算法的有效性,设置3 个点目标位置分别为(-5,8),(0,10.5),(2,13),利用所提算法进行仿真后得到的结果如图7 所示,点目标放大结果和距离向及方位向剖面图如图8、图9 所示。可以看出3 个点目标经过PFA 成像及几何失真校正后均在正确位置上,误差很小,可以忽略不计,说明上述基于子孔径拼接的成像方法是有效的。
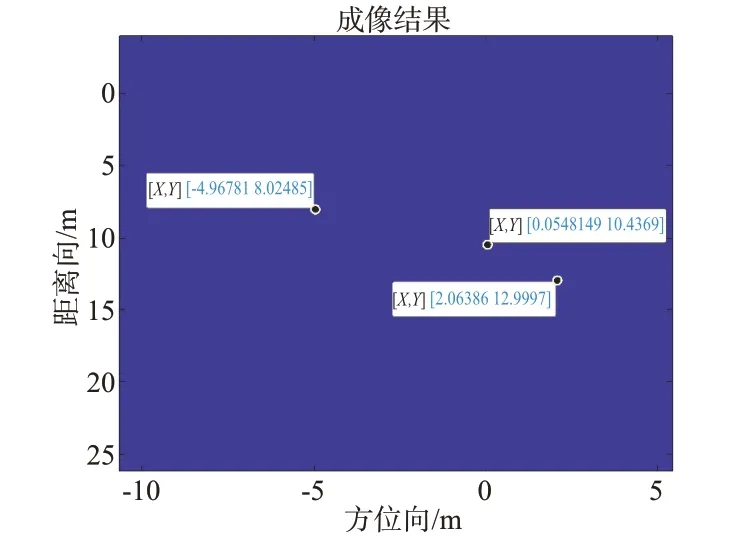
图7 点目标仿真结果

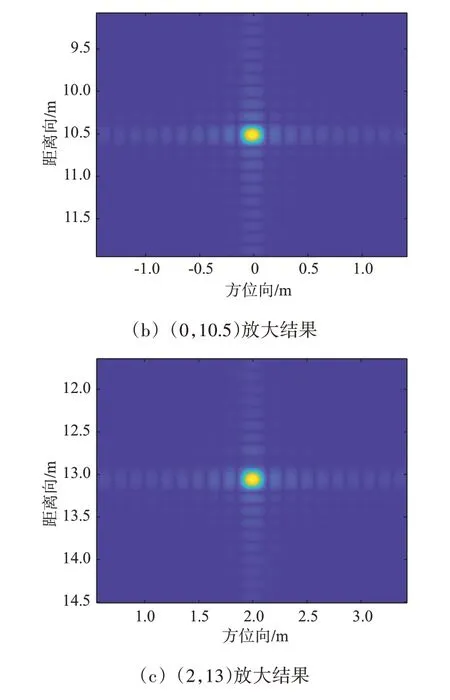
图8 点目标放大结果

图9 方位向和距离向剖面图
2.2 面目标仿真
设置如图10(a)所示的面阵,相邻点间方位向间隔和距离向间隔均为2 m,距离向长度共6 m,方位向长度14 m,共计28 个点目标。其成像结果如图10(b)所示,方位向回波脉冲数共有16 384 个,子孔径脉冲设置为1 024 个,划分为16 个子孔径,其中第1,3,5,7 个子孔径几何失真校正前后的成像结果如图11 和图12 所示。从图11 可以看出,PFA成像使用的平面波假设与实际球面波不符,存在较大的误差,使成像结果扭曲、变形、错位,又由于车载情况下一般是对近场景成像,平面波假设带来的影响更大,因此要弥补这些误差。如图12所示,经几何失真校正后误差几乎被补偿掉了,目标成像结果与设置相同。

图10 面阵及其成像结果

图11 经PFA后子孔径成像结果

图12 几何失真校正后子孔径成像结果
2.3 实测数据处理
本文实测数据使用IWR1843 毫米波雷达模块发射和接收毫米波,经DCA1000 高速捕获原始数据后通过网线传给计算机。在实际应用场景中,IWR1843毫米波雷达使用的参数如表2所示。
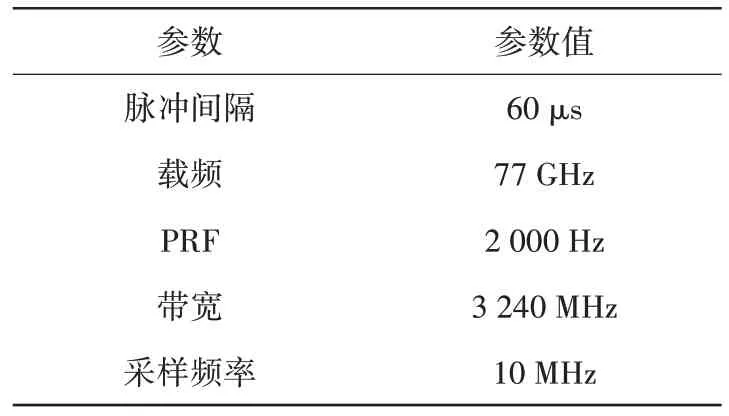
表2 实测数据参数
首先在校内停车坪采集了一组斜视数据,斜视角为30°,车速为10 km/h,全孔径共划分为113个子孔径,每个子孔径包含512 个脉冲。图13 和图14 为第91~95 个子孔径几何失真校正前后的成像结果对比。由图13 可以看出,由于子孔径回波在经过PFA 处理后存在一定角度的旋转以及几何位置的失真,导致图像混乱,目标不在正确的位置上,不能直接拼接。经几何失真校正后,目标位置正确,子图像可连续拼接。

图13 几何失真校正前子孔径成像结果

图14 几何失真校正后子孔径成像结果
图15为条带实测数据成像结果及其与实际成像场景的对应情况。在图15 中可以看到,经过子孔径划分、PFA成像、几何失真和子孔径拼接后,得到了停车坪连续完整的成像结果,车辆和草坪均成像在正确的位置,路灯(红色框内)、指示牌(黄色框内)清晰可见,实现了良好的聚焦。由于实现过程中滤波后的波束仍然较宽,所以未重叠子孔径。

图15 校内停车坪成像结果与实际场景的对应情况
图16为在校外公路采集的一组斜视数据的成像结果及其与实际场景的对应情况,将波束滤波较窄,使用重叠子孔径的方式对其进行成像。图16 全孔径回波脉冲共有95 342 个,成像时子孔径回波脉冲为512 个,重叠率rate≈52%,即每两个相邻子孔径间有约270 个脉冲相互重叠。成像之后,路边车辆均停放在其实际所在位置上,说明了算法的有效性。

图16 校外公路成像结果与实际场景的对应情况
3 结束语
本文提出了一种改进的PFA 算法,依据聚束数据与条带数据间的联系,将全孔径数据划分为子孔径,利用PFA 进行子孔径成像,并通过几何失真校正解决了成像扭曲变形的问题。同时,为了保证成像的高分辨率,在一定条件下以重叠子孔径的方式划分全孔径。根据点目标及实测数据的成像结果可以看出,该算法能够解决车载毫米波雷达大斜视时两维耦合严重的问题,在车载毫米波雷达成像领域中具有良好的应用前景。本文重在研究成像算法,虽然上述分析均基于雷达匀速运动进行,但是成像结果满足当前分辨率的要求。随着对分辨率要求的提高,实际行车过程中由于速度不均而带来的目标散焦等问题将在后续工作中进行深入研究。

