海杂波多普勒谱Hurst指数特性分析及目标检测

董云龙，张兆祥，刘宁波，黄 勇，丁 昊

（海军航空大学信息融合研究所，山东烟台 264001）

0 引 言

对海面漂浮小目标进行检测是对海探测雷达的主要任务之一，此类目标主要包括浮标、小船、水雷和飞机残骸等，具有雷达回波微弱的特点［1-3］。基于统计理论设计的似然比检测器实际上是一种能量检测器，其性能极易受到信杂比（Signal-Clutter Ratio,SCR）和海杂波幅度分布类型的影响。在高分辨率、低擦地角和高海况情形下，通常存在大量海尖峰，海杂波具有明显的非平稳、非均匀和非高斯特性，似然比检测器无法实现漂浮小目标的有效检测，且存在高虚警率的突出问题［4-5］。

分形特征作为一类非能量特征，能够在一定程度上克服SCR 的影响，自提出以来就受到人们的广泛关注［6］。为描述自然界广泛存在的不规则几何，1980 年，Mandelbrot 教授介绍了分形几何的基础［7］。海、陆、云和山的表面非常粗糙，这表明它们是分形表面。1990 年，人们证明了分形表面的散射信号仍然是分形信号［8］，这激发了分形几何在雷达探测中的应用。1993 年，Haykin 等人首次将单尺度分形维数运用于雷达目标检测［9］。单分形参数只能从整体上描述集合的分形特性，为此Kaplan 等人研究了分数布朗运动（Fractional Brownian Motion, FBM）的扩展自相似特性［10］，文献［11］研究了海杂波的多重分形特性。为改善时域信号的SCR，增大海杂波和目标回波的分形特性区分度，人们研究了海杂波频谱（本文将频谱称为多普勒谱）、AR 谱和分数阶傅里叶变换谱的分形特性，提出了众多变换域分形特征［12-16］，多普勒谱Hurst 指数是其中之一。多普勒谱Hurst 指数能够从整体上描述多普勒谱的分形特性，兼顾相参积累和分形特征的优势，具备较强的实际应用价值。然而人们对分形类特征检测方法的研究存在两点不足：一是没有深入研究参数选择、极化方式和海况因素对海杂波分形特征特性的影响，这导致分形特征很难应用于实际；二是人们往往通过蒙特卡洛仿真或非参量恒虚警（Constant False Alarm Rate,CFAR）方法确定判决门限，蒙特卡洛仿真方法确定判决门限需要计算大量数据，非参量CFAR 方法为实现恒虚警会带来较大的检测性能损失。

鉴于此，针对已有研究的不足，本文对海杂波多普勒谱Hurst 指数的统计特性进行研究，引入合适的CFAR 检测器确定判决门限，以期为多普勒谱Hurst 指数的实际应用提供支撑。本文首先基于实测数据，分析参数选择、极化方式和海况等级对海杂波多普勒谱分形特性及多普勒谱Hurst指数统计特性的影响；其次使用6 种常见的统计分布模型对实测海杂波多普勒谱Hurst 指数的分布类型进行验证，并在此基础上设计了一种基于多普勒谱Hurst 指数的恒虚警检测器；最后使用实测数据验证了所提目标检测方法的有效性。

1 基本理论

大量文献已经证明时域海杂波可以使用FBM模型进行建模［17］，事实上，海杂波频谱（多普勒谱）仍具有自相似性，可当作分形集处理。本节简要说明对海杂波频谱（多普勒谱）进行分形特性分析的理论方法。

1.1 FBM在多普勒域的自相似性

FBM 模型可以用来建模海杂波，文献［12］对时域FBM 模型BH(t) 的频谱进行理论推导，得到下式：

其中时域FBM 模型BH（t）定义在时间区间（0,T1）内，t′=κt是推导时的尺度变换，FB(f)是FBM 的频谱，κ为尺度变换系数，H为Hurst指数，表示在统计意义下相等。FBM 模型BH(t) 的功率谱满足以下等式：

SB(f)是FBM 的功率谱。通过式（1）和式（2）可知，如果频率尺度变为原来的1/κ，那么频谱密度变为原来的κH+1，而功率谱密度变为原来的κ2H+1，这个尺度关系说明FBM的频谱、功率谱密度都是频率的幂函数，均具有统计意义上的自相似性，故可直接使用分形理论对海杂波的频谱（多普勒谱）进行处理。统计意义上自相似性成立的尺度区间称为无标度区间，为与时域中的无标度区间区分，本文将在频域中自相似性成立的区间称为频率无标度区间。

1.2 多普勒谱Hurst指数的计算

假设高分辨率对海探测雷达，在某波束方位上发射长度为N的相干脉冲串，并在某距离单元上接收到长度为N的海杂波序列x(n),n=1,2,…,N，通过快速傅里叶变换（Fast Fourier Transform, FFT）得到其多普勒谱X(k),k=1,2,…,K，将其建模为“随机游走”模型，验证其是否满足以下关系：

若满足式（3）的幂律关系，则认为多普勒谱序列是分形体。其中F(m)为配分函数；m为频率采样间隔，即频率尺度；H为多普勒谱序列的Hurst 指数，即海杂波的多普勒谱Hurst指数，Hurst指数能够从整体上描述分形特性。事实上，海杂波多普勒谱的自相似性仅存在于其频率无标度区间内，即在此无标度区间上，海杂波多普勒谱具有分形特性。双对数坐标系中，log2(F(m))与log2(m)在频率无标度区间上通过直线拟合得到的斜率即为多普勒谱Hurst指数，可通过下式描述：

实际上，也可通过判断log2(F(m))与log2(m)是否具有线性关系，判断海杂波多普勒谱是否具有分形特性。

2 实测海杂波多普勒谱Hurst 指数统计特性分析

2.1 实测数据简介

本文所做实验均基于实测数据完成，实测数据来自两个公开的数据集。一是IPIX 雷达数据集中1993 年采集的10 组数据，每组数据包含HH、VV、HV、VH 四种极化模式数据，每组数据含14 个距离单元。数据采集时，雷达工作于凝视模式，凝视时间约131 s，脉冲重复频率（Pulse Repetition Frequency, PRF）为1 kHz，距离向分辨率为30 m，目标为金属丝包裹的直径1 m的漂浮小球［18］，更详细数据介绍见表1。

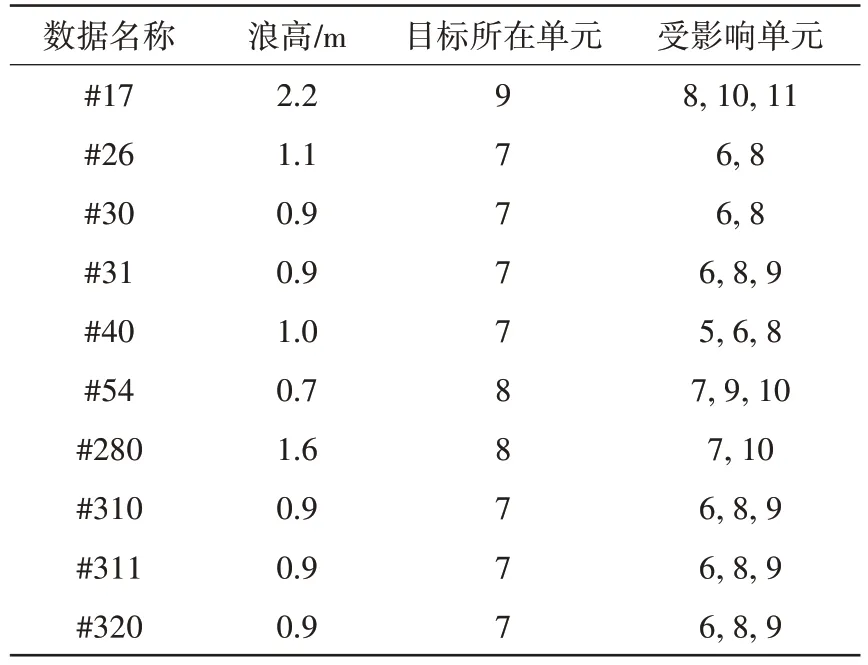
表1 1993年IPIX雷达数据说明

二是海军航空大学“雷达对海探测数据共享计划”数据集（2020年第1期）。该数据集主要包括不同海况等级下的海杂波和目标回波数据，数据采集时，雷达主要工作于凝视模式，极化方式为HH 极化，距离向采样率为60 MHz，雷达架高80 m，PRF 为1.6 kHz［19-20］，更详细数据介绍见文献［19］和表2，每个数据编号包含2 至3 组数据，本文采用序号代替相应数据编号对数据进行引用。

表2 “雷达对海探测数据共享计划”数据介绍

2.2 海杂波多普勒谱分形特性及多普勒谱Hurst指数统计特性的影响因素

分析不同因素对海杂波多普勒谱Hurst 指数统计特性影响的同时，也需要分析不同因素对海杂波多普勒谱分形特性的影响，以确定不同条件下计算多普勒谱Hurst 指数的参数选择规则。海杂波多普勒谱分形特性及多普勒谱Hurst 指数统计特性的影响因素众多，本文主要研究时间序列长度（脉冲数）、FFT 的频率点数、雷达极化方式和海况等级的影响。需要注意的是，本文分析均采用“随机游走”模型对多普勒谱进行建模。

首先分析脉冲数对海杂波多普勒谱分形特性及多普勒谱Hurst指数统计特性的影响。FFT点数设为216，HH#26 数据在不同脉冲数下得到的典型多普勒谱配分函数如图1所示。可知，脉冲数对频率无标度区间存在影响，脉冲数越多，配分函数无标度区间线性程度越好。当脉冲数足够长时（大于210），频率无标度区间范围始终保持在25～210；脉冲数较少时（远小于210），频率无标度区间范围明显缩小。这主要是由于脉冲数越少，频率分辨率越差，多普勒谱配分函数的计算误差越大导致。实际检测过程中，为减小多普勒谱Hurst 指数的计算误差，时间序列长度一般取210及以上。图2 展示了脉冲数对海杂波单元和目标单元多普勒谱Hurst 指数统计分布的影响，其中数据是HH#311，FFT 点数均为216，频率无标度区间为25～210。本文使用概率密度函数（Probability Density Function，PDF）刻画多普勒谱Hurst指数的分布情况。显然，随着脉冲数的增加，海杂波多普勒谱Hurst 指数分布的收束性变好，拖尾变短，海杂波单元和目标单元提取多普勒谱Hurst 指数的整体分离程度增加。这表明虚警概率一定时，目标检测的正确检测概率有增大的趋势。

图1 脉冲数对多普勒谱分形特性影响

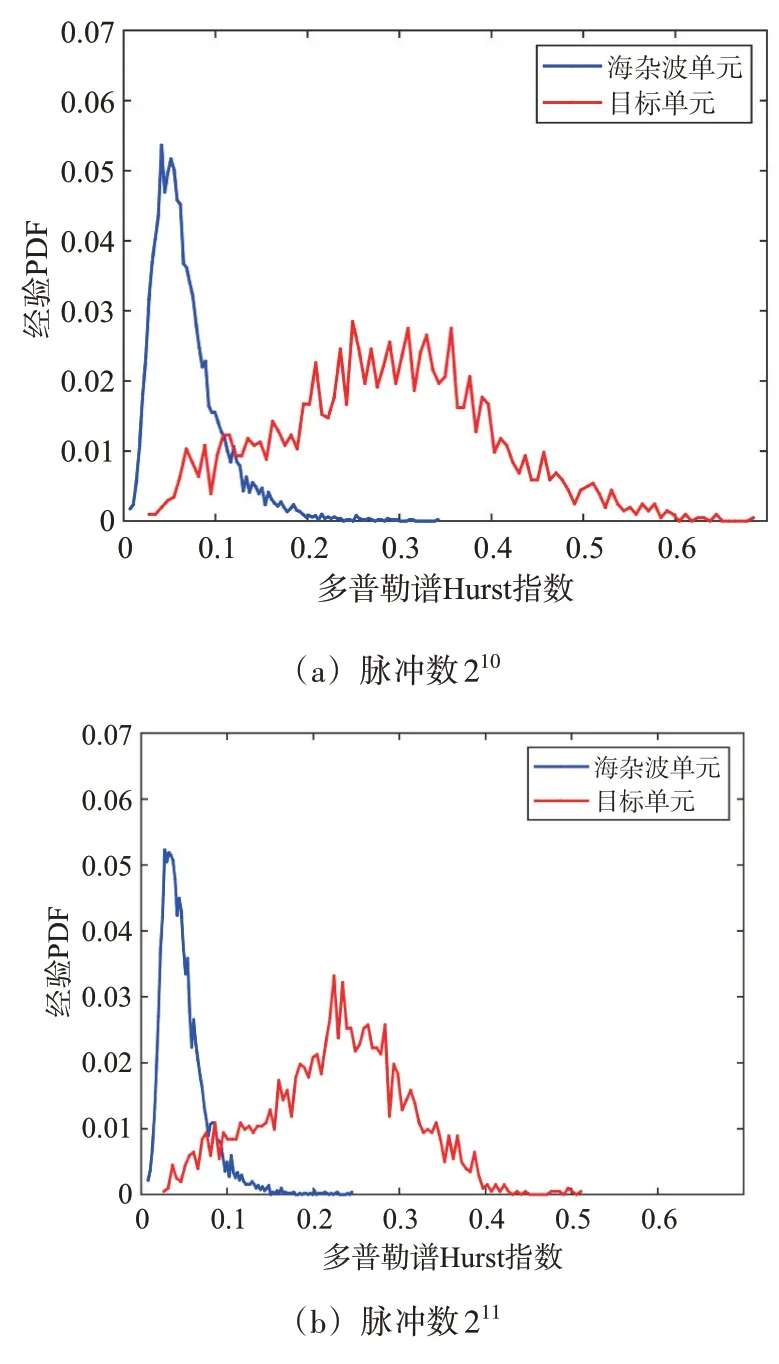
图2 脉冲数对多普勒谱Hurst指数分布影响

FFT 点数对海杂波多普勒谱分形特性及多普勒谱Hurst 指数统计特性也存在影响。时间序列长度设为211，HH#311 数据在不同FFT 点数下得到的典型多普勒谱配分函数如图3所示。可知，随着FFT点数的增加，频率无标度区间的范围在逐渐增大，配分函数的线性程度无明显变化。由于Fourier 变换是一种线性变换，FFT 点数增大，并不会明显改变多普勒谱的自相似结构，所以频率无标度区间范围随FFT 点数增大而近似线性增大，配分函数的线性程度基本不变。图4 展示了FFT 点数对海杂波单元和目标单元多普勒谱Hurst 指数统计分布的影响，时间序列长度均为211。随着FFT点数的增加，海杂波多普勒谱Hurst 指数分布的收束性和拖尾并无明显变化，但海杂波单元和目标单元提取多普勒谱Hurst 指数的整体分离程度明显增加。这表明虚警概率一定时，正确检测概率有增大的趋势。综上分析可知，实际应用过程中，为提升检测性能和便于选择频率无标度区间，FFT点数可固定为216，时间序列长度足够时，频率无标度区间基本为25～210。

图3 FFT点数对多普勒谱分形特性影响

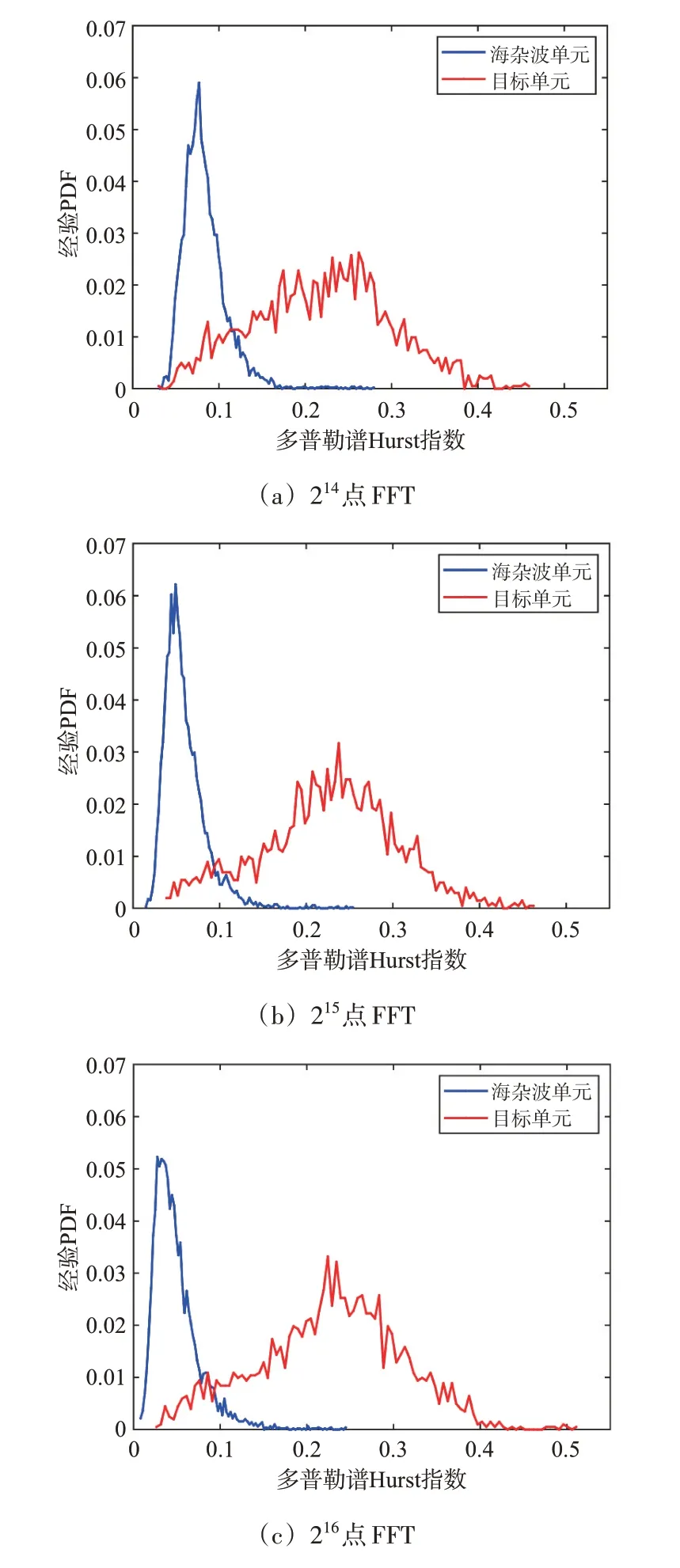
图4 FFT点数对多普勒谱Hurst指数分布影响

其次分析雷达工作极化方式对海杂波多普勒谱分形特性及多普勒谱Hurst 指数统计特性的影响。时间序列长度均为211，FFT 点数为216，#311数据在4 种极化方式下得到的典型多普勒谱配分函数如图5所示。显然，极化方式对于海杂波多普勒谱配分函数的无标度区间无明显影响。图6 展示了极化方式对海杂波单元和目标单元多普勒谱Hurst 指数统计分布的影响，其中时间序列长度为211，FFT 点数为216，频率无标度区间为25～210。可知VV 极化时，海杂波多普勒谱Hurst 指数分布的聚集性最好，拖尾最短；HV 极化和VH 极化效果基本一致，HH 极化最差。4种极化方式下，海杂波单元和目标单元提取多普勒谱Hurst 指数的整体分离程度基本相同。这表明使用多普勒谱Hurst 指数进行目标检测时，VV 极化数据效果最佳，其次是HV和VH极化，HH极化效果最差。

图5 极化方式对多普勒谱分形特性影响

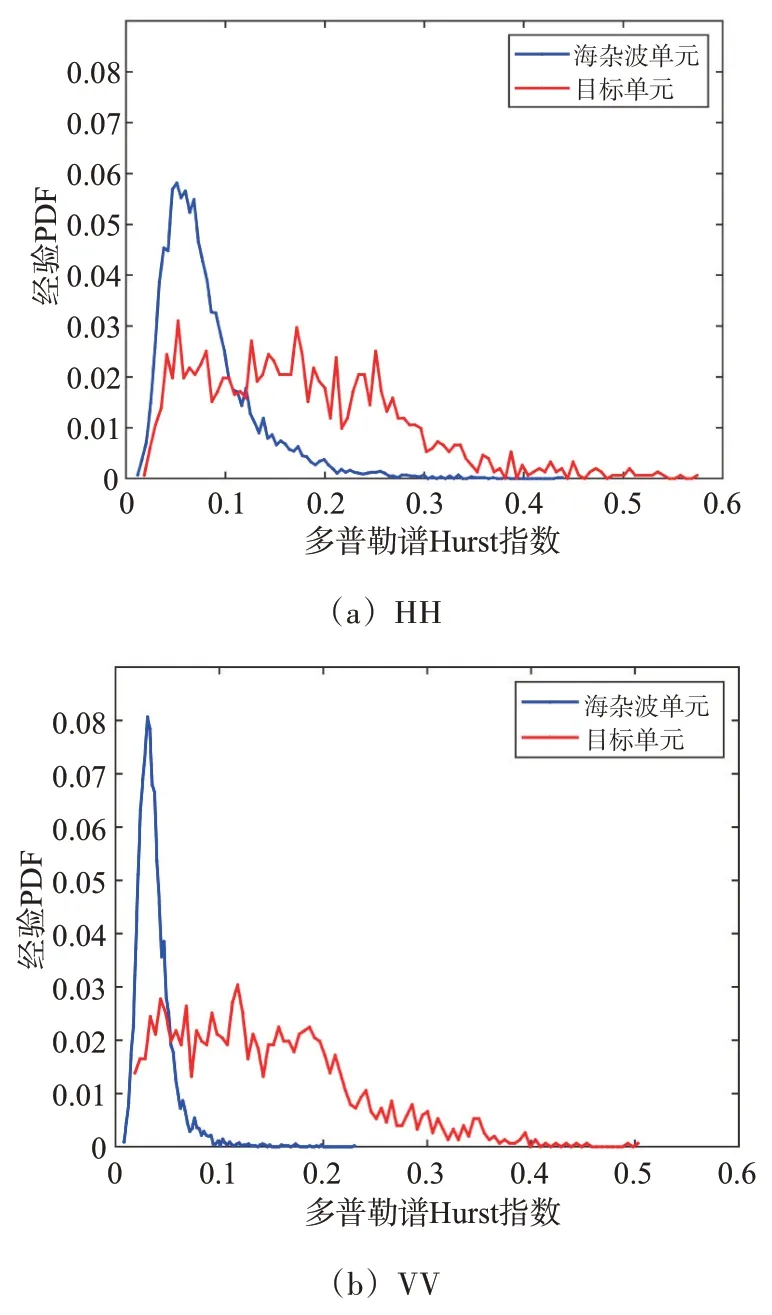
图6 极化方式对多普勒谱Hurst指数分布影响

以往研究已经证明海况等级对海杂波分形特性存在明显影响［17］，海况等级对海杂波多普勒谱分形特性同样存在影响，本文主要分析不同海况对海杂波多普勒谱分形特性及多普勒谱Hurst 指数统计特性的影响。时间序列长度均为211，FFT点数为216，2 级海况和3、4 级海况数据的典型多普勒谱配分函数如图7 所示，其中2 级海况为数据2，3、4 级海况为数据6。显然，2 级和3、4 级海况对应的海杂波多普勒谱配分函数的无标度区间基本相同，均为25～210。图8 展示了海况等级对海杂波单元和目标单元多普勒谱Hurst 指数统计分布的影响。可知，海况等级越高，海杂波多普勒谱Hurst指数分布的聚集性越好，拖尾越短。一般情况下，海况等级和有效浪高越高，海面的白浪、破碎浪越多，海面粗糙度越大，海杂波多普勒谱的不规则程度增大，而Hurst 指数表征了分形集的粗糙度和不规则程度，故高海况海杂波的多普勒谱Hurst 指数整体偏小。4级海况时，海面已比较粗糙，2级海况时，仍存在较多的规则海面，故整体而言，4 级海况海杂波多普勒谱Hurst 指数的统计分布拖尾较短、聚集性更好。事实上，有效波高和海况等级越高，海面粗糙度存在变大趋势，但并不一定更大，这与有效波高计算方法和海况等级的划分标准有关，详情见文献［20］。这表明随着海况等级和有效浪高的增加，海杂波多普勒谱Hurst 指数的统计分布具有聚集性变好、拖尾变短的趋势。需要注意的是，这并不说明海况等级越高，海杂波单元和目标单元所提取多普勒谱Hurst 指数的整体分离程度越好，因为当海况等级足够大时，目标单元的SCR过低，海杂波单元和目标单元提取多普勒谱Hurst指数的分离程度反而变差。

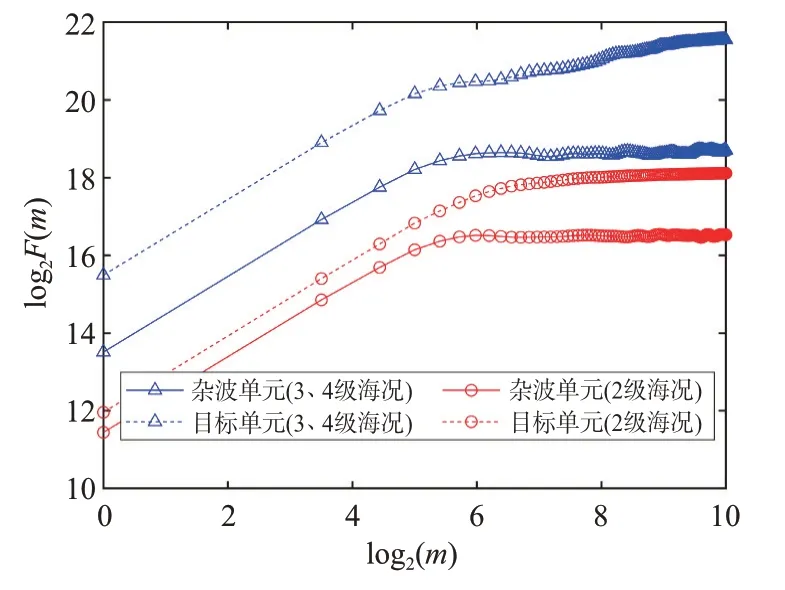
图7 海况等级对多普勒谱分形特性影响

图8 海况等级对多普勒谱Hurst指数分布影响

经过上述分析，可得出以下结论：当使用多普勒谱Hurst 指数进行目标检测时，为提升检测性能，应首选VV极化数据，其次是HV和VH极化，最差是HH 极化；时间序列长度足够长时（一般不少于210），最佳FFT 点数为216，此时最佳频率无标度区间为25～210；当时间序列长度远小于210或FFT 点数变化较大时，会影响最佳频率无标度区间范围；海况等级在2～4 级之间变化时，不会影响上述结论。

2.3 海杂波多普勒谱Hurst指数的统计特性分析

基于表1和表2中介绍的47组实测数据，利用6 种经典统计分布模型（高斯分布、瑞利分布、韦布尔分布、对数正态分布、K分布和KK分布），本文验证了海杂波多普勒谱Hurst指数的最佳统计分布类型，以便设计相应的恒虚警检测器。从47组实测数据中提取海杂波单元多普勒谱Hurst指数，利用6种分布模型分别对其进行拟合，使用卡方检验的拟合误差值大小判断模型拟合适用度，得到的实验结果如图9 和表3 所示。其中脉冲数为210，FFT 点数为216，频率无标度区间为25～210。

图9 典型海杂波多普勒谱Hurst指数分布的拟合与误差结果

表3 实测海杂波多普勒谱Hurst指数分布拟合最小误差统计

47 组实测数据中，45 组数据的最佳分布类型是对数正态分布，只有2组数据的最佳分布类型为韦布尔分布，这说明实测海杂波多普勒谱Hurst 指数的最佳分布类型基本为对数正态分布。47 组数据包含了2～4 级海况、4 种极化方式下的数据。显然，海况和极化方式的不同不会改变海杂波多普勒谱Hurst 指数的最佳分布类型，事实上，脉冲数的改变也不会影响最佳分布类型。

3 基于多普勒谱Hurst 指数的目标检测方法

上文已经指出，对数正态分布是海杂波多普勒谱Hurst指数的最佳分布类型，Log-t检测器是在形状和尺度参数都未知的韦布尔或对数正态杂波中提供CFAR 检测的一种准最优单脉冲检测策略。故本文将Log-t 检测器引入，设计基于多普勒谱Hurst指数的CFAR检测器，检测流程如图10所示。

图10 基于多普勒谱Hurst指数的目标检测方法流程图

其中，Log-t CFAR检测器的检测统计量如下：

Y0是待检测单元提取多普勒谱Hurst 指数的对数变换值，Yi,i= 1,2,…,R是参考单元提取多普勒谱Hurst 指数的对数变换值，R表示参考单元数目。判决门限T可通过下式计算：

Pfa为提前给定的虚警概率。需要注意的是，在提取多普勒谱Hurst 指数过程中，参数设置规则如上文所述，即当脉冲数足够（一般不少于210）、FFT 点数为216时，频率无标度区间为25～210；当脉冲数远小于210或FFT 点数变化较大时，需要改变频率无标度区间。

4 检测性能分析

使用IPIX 数据集验证所提目标检测方法的有效性。实验过程中，1 024 个脉冲计算一次多普勒谱Hurst 指数，FFT 点数设为216，频率无标度区间为25～210，虚警概率Pfa为0.001。为比较分析，本文使用文献［21］所提三特征检测器、时域多重分形检测器［11］和散斑一致性因子检测器［22］进行了对比实验，其中提取单个特征所使用脉冲数均为1 024。检测结果如图11 所示，可知本文所提检测方法在VV 极化数据中效果最佳，其次是HV 和VH 极化，HH 极化效果最差，这与上文分析结果相同。通过比较发现，4种检测器中，本文所提检测器在VV 极化数据中的检测效果能达到最佳，在HV、VH 和HH 极化数据中效果不如三特征检测器；在4 种极化数据中的检测效果基本都优于时域多重分形检测器和散斑一致性因子检测器，这表明本文所提检测方法具有较好的小目标检测性能和稳定性。

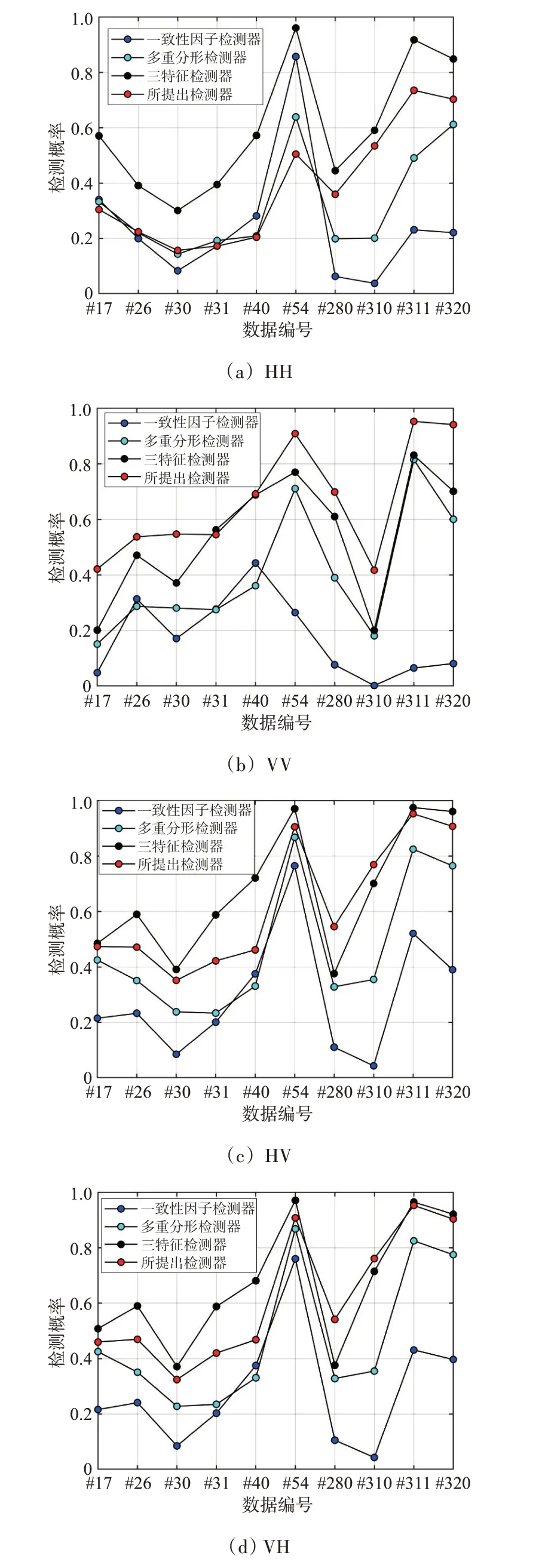
图11 所提检测器与其余检测器的检测概率

表4 给出了4 种检测器在#40 数据中的其他检测结果。可知，当使用脉冲数为512 时，所提检测器的正确检测概率小于0.5，主要原因有两点：一是脉冲数过少，频率分辨率较差，多普勒谱配分函数和多普勒谱Hurst 指数计算误差较大；二是相参积累之后的SCR 仍较低。随着脉冲数增加，4 种检测器的正确检测概率均有所提升，其中分形类特征检测器的提升比例最大；脉冲数为1 024 和2 048时，所提检测器在VV 极化数据中的性能基本达到最佳。

表4 4种检测器的其他检测概率

5 结束语

本文基于实测数据，详细分析了时间序列长度（脉冲数）、FFT 点数、极化方式和海况等级对海杂波多普勒谱分形特性及多普勒谱Hurst 指数统计特性的影响，并给出了相关结论，为多普勒谱Hurst 指数实际应用于目标检测提供了支撑。其次，本文利用6种常用统计分布模型（高斯分布、瑞利分布、韦布尔分布、对数正态分布、K 分布和KK分布），验证了海杂波多普勒谱Hurst 指数的最佳统计分布模型为对数正态分布，且海况等级、极化方式和脉冲数的改变基本不会影响其最佳分布类型。最后，结合多普勒谱Hurst 指数与Log-t CFAR检测器，提出了基于多普勒谱Hurst 指数的CFAR检测算法。实测数据测试结果表明，本文所提检测器具有较好的小目标检测性能和稳定性，且在VV极化数据中性能最佳。