基于差分模型的近场无源定位算法
赵 研,陶海红,畅 鑫,董春曦,赵国庆
(1.西安电子科技大学雷达信号处理全国重点实验室,陕西西安 710071;2.西安电子科技大学电子工程学院,陕西西安 710071)
0 引 言
辐射源定位是目标探测领域的重要应用,在雷达、地震、声学、海洋和声呐等专业有着广泛的需求。无源定位问题按照阵列孔径、目标距离和工作波长的关系可以分为两分支,(a)典型天线阵列远场条件(r≥2D2/λ)和(b)天线阵列近场条件,其中r是目标到天线阵列的距离,D是阵列孔径,λ是目标信号的波长。在远场条件下,波达方向(DOA)是分析天线阵列平行波前[1]信号传播过程,经过多年研究目前已经取得了长足发展和大量成果。当满足近场条件或者满足菲涅尔区条件时,电波波前不再满足平行假设,传统单要素线性DOA 角度估计方法不再适用,但也具备了解算目标未知的可能(同时估计目标角度和距离)。本文针对典型近场辐射源定位问题,通过对于距离和角度的非线性联合分析可获得目前位置信息。
近场目标定位近些年是较为热门的问题,传统上采用的方法有:1)经典采用多重用户分离(MUSIC)的二维拓展算法[2];2)利用菲涅尔近似波前的二阶表达式估计[3],在此基础上利用陶布利兹矩阵旋转不变性,进行ESPRIT 的DOA 估计[4]或高阶累积量的DOA 估计[5];3)通过菲涅尔近似的特殊阵列结构协方差矩阵构造,可以建立角度的单维问题,并由此通过MUSIC 估计距离[6-8],利用MUSIC 代价函数估计最佳值[9-10],此外基于子阵远场估计模型,还提出一种三角函数近场逼近方法[11]。然而以上的方法都是通过二维要素的一维空间化简求解过程。
不同于传统近场目标辐射传播的菲涅尔近似模型,基于近场空间几何结构和三角函数关系推导得到新的差分迭代模型[12],本文建立全新高精度目标关系模型并形成定位解析表达式,通过阵列处理估计TOA 定位观测量,利用新定位算法快速准确地获取近场多个独立同分布目标的定位信息。
1 近场菲涅尔近似目标定位
对于均匀线阵(ULA),近场目标二维定位的几何模型如图1 所示。其中均匀线阵包含N个天线阵元,相邻阵元的间距为d,其中原点阵元、第i个阵元和第k个目标,在三角形ΔOIK中,从O到K的距离为rk,从第I个阵元到K的距离为rik,而阵列方向和rk之间夹角为θk,阵列方向与rik之间的夹角为θik,对于三角形ΔONK,依据余弦定理有

图1 近场目标定位结构示意图
参见图1,(rnk,θnk)代表第k个辐射源对第n个节点的距离和到达角,假设λ为电波波长,则传输的相位延迟为
式中Rs是目标信号协方差矩阵。求解近场目标数量和位置的问题变成了对采样数据序列M个样点的估计。针对式(6)传统研究提出了多种处理方法,基于WVD 的分析估计[3],基于子阵远场估计(MUSIC/ESPRIT)的统计分析[4,6,11],4 阶累积量的子空间分析[5],通过分析二阶协方差矩阵数学模型,构造特殊选择节点阵列,抵消数学结构中的二次项而只保留一阶线性相移项,通过对表达式的算法模型估计[7],得到最优化目标位置估计逼近值[8-10]。
2 基于差分模型的定位新算法
不同于传统的菲涅尔近似,文献[12]中,作者提出一种新的近场电波传播近似模型,其结构与初值和迭代次数相关,可知[12]
2.1 基于二次迭代的定位分析


2.2 基于三次迭代的定位分析
传统的定位算法都是基于菲涅尔的二阶近似关系式进行推导估计,其性能会继承近似基础误差影响,而按泰勒级数展开三阶近似虽可提升近似精度,但所产生的二元三次方程组难以获得可行解。基于差分迭代新模型,可获取对于目标定位的三次迭代新算法,有[12]
令x= cosθk,由此建立方程:
令n= 1,2建立方程组
由于表达式(18)存在规则的结构形式,使得方程组(19)消元操作较为便捷,可将二元三次方程转化为一元三次方程,而后者存在通解公式,并由此获得(rk,θk)实数形式的非零可行解,由于具体解数学表达式较长,可通过数学工具软件解得,此处不再赘述。
新算法的特征优势在于基于较高精度的近场传播近似模型条件下建立了定位方程,使得模型自身的基本估计误差优于传统菲涅尔近似的结果[12],也使得其数学表达式非线性特征要更为强烈。但是正如上面所推导,其结构的规律性使得二元三次复杂方程组依旧可推导和存在闭式结构的解析可行解。基于传统菲涅尔近似条件下,以往算法表达式具有了更良好的线性特征和简洁数学结构,通过经典的最优化估计、子空间分解或累积量分析都可以得到一定准则下的最优定位参数解,但其算法运算量往往较大,对很多实际客观存在的非线性误差适应性低,新算法采用了更加精准的近场模型,并且推导定位参数闭式解,在保证精度的同时使得后续实际应用中数值计算存在很大的自由度,为进一步精简高效运算提供可能。
2.3 相关处理与算法性能分析
在近场阵列辐射源定位的整体信号处理过程中,各通道输入信号间一般都满足相互独立且随机同分布,噪声为加性高斯的前提假设,因此对于实际阵列条件下式(4)可对等表示为
式中△tnl==rnk/C。
对于式(5)有
由此可得所提算法输入参数△Rnk= △tnkC。对于TOA 的精确估计还可以参考其他算法文献[13-15],本文主要重点在后面的基于TOA 定位观测量的定位算法研究,这里不再赘述。
从文献[12]的性质分析,可以看到新的算法模型(二次迭代)与传统菲涅尔近似模型(二阶近似)算法仿真分析,两者在象限区间中各有一般的近似优势;而如果采用优化初值的三次迭代新算法则近似程度明显提高,在0°~82°和97°~180°近场范围内近似精度都显著提高,参见图2。由此可知在高信噪比条件下(数值精度可分辨情况下),新算法的定位精度应优于菲涅尔近似的定位精度。
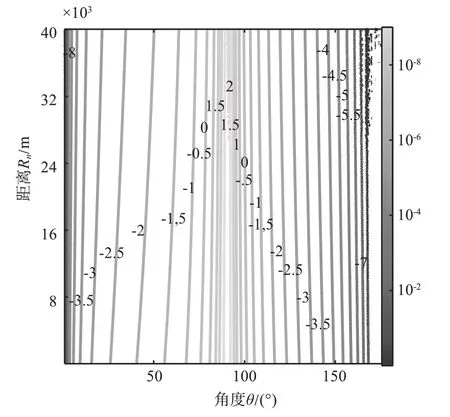
图2 所提算法与TSECL2rd定位误差对比图
3 对所提算法仿真和性质分析
针对均匀线阵的近场区域范围内目标定位性质进行仿真分析,对比分析实验:1)针对近场阵列的子阵远场分解及多个参数回归分析估计算法[11];2)基于菲涅尔近似建立的定位方程二阶条件求解[3],参见式(16);3)基于高阶累计量的阵列统计估计定位方法[5];4)文献[12]提出基于二次差分迭代计算定位方程新算法,参见式(14);5)本文所提出基于三次差分迭代计算定位方程新算法,由于其目标定位参数闭式解结构较为复杂,具体参见附录。
由图3 可知,随着信噪比条件(噪声比S/N=Psignal/Pnoise,其中Psignal为信号能量,Pnoise为与信号时、频等域相匹配噪声能量)从-20 dB 到30 dB 以1 dB 的步长逐渐变换,高阶累计量算法的测距精度最高误差在1%左右;所提出三次迭代比二次迭代算法精度略高,也逼近1%的误差水平,指标性能分别为第2 和第3;菲涅尔近似算法与远场子阵定位算法由于具有噪声分解与原始数据信息测量优势,在低信噪比条件下效果相对较好,但整体定位性能相对较差。

图3 各种算法测距误差随信噪比变化性能图
由图4可知,随着信噪比条件从-20 dB到30 dB以1 dB 的步长逐渐变换,从曲线结果可知所提出三次迭代定位算法具有优良的近场模型非线性特征适应能力,在大于0 dB 信噪比具有良好的测角性质,测角误差约1.1%;而高阶累计量算法的测角精度也较为优秀,误差也逼近1%,两者性能较优且逼近性能渐近线;文献[12]提出二次迭代算法精度要好于远场子阵定位算法和菲涅尔近似定位算法,而这两种算法在低信噪比条件下的性能要优于前面的算法。
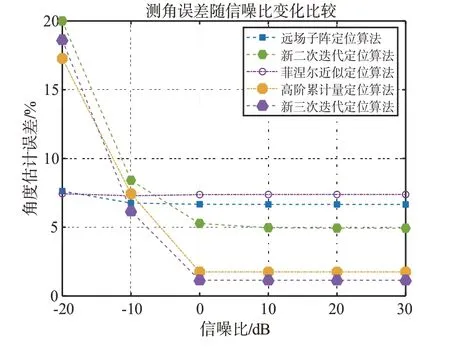
图4 各种算法测角误差随信噪比变化性能图
通过对于近场目标距离和角度的综合测量评估,5种典型方法的定位误差对比如图5所示。
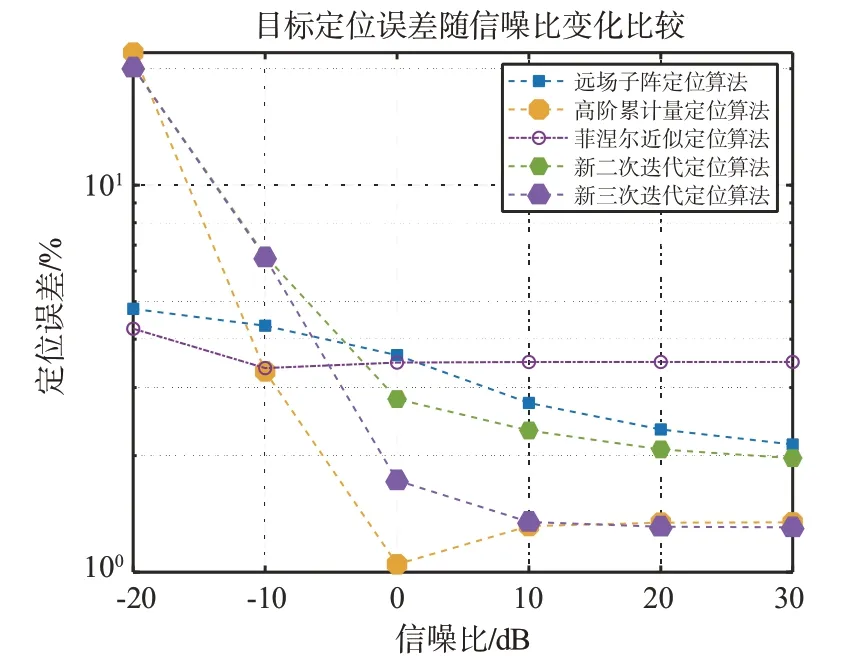
图5 各种算法定位误差随信噪比变化性能图
由图5 可知,5 种近场定位方法整体定位误差随信噪比提升而改善。而其中新提出的三次迭代估计误差与高阶累积量估计方法的定位指标最好,均在1%左右,且两者误差值十分接近,且在负信噪比条件下性能较差,并随着信噪比提升误差快速减小;新提出二次迭代方法的误差估计性能弱于前两种算法,但在高信噪比条件时,性能要优于远场子阵估计和菲涅尔近似定位方法;而这两种定位算法在低信噪比条件性能相对稳定,误差恶化程度减小。
4 结束语
本文所提算法具有3个优点:1)具备代数差分迭代结构形式,可以实现近似精度更高的闭式解析定位解表达式,其三次迭代解结构是同阶次菲涅尔近似难以推导得到的高精度解;2)通过高精度逼近的传播模型迭代推导得到的近场定位算法,可以得到正信噪比条件下和高阶累积量定位算法误差基本相同的定位结果能力;3)在相同阵列近场正信噪比工作条件下,新三次迭代算法与高阶累计量定位误差性能较好,相比其他方法定位性能改善0.3%~3%,而本方法是代数计算与结果统计,相比于最优化分析和最佳点估计过程,其计算分析过程与数值计算量大为降低,处理复杂度和时间代价更低。本文所提算法优势和特征较为突出,对于近场DOA问题的解决提供新思路。

