基于不同机器学习算法的铝合金性能预测

李 婷

(沈阳东创贵金属材料有限公司,辽宁 沈阳 110000)

0 引言

可持续的绿色发展方式是当今世界的主旋律,对材料的性能也提出了高强度、低重量的高标准要求,尤其是在航空航天领域,降低材料的重量可以减少油耗、增加航程,7xxx 系铝合金正是这样一种材料[1]。7xxx 系铝合金最早在1932 年由维贝尔发现,随后通过调整合金成分、添加微量元素,又发展出很多新合金,使得7xxx 系铝合金种类增多,作为高强度铝合金的代表,以其较高的强度以及良好的韧性和耐蚀性等优异性能而被广泛地应用于航空航天及交通运输领域[2-5]。

实验试错法是材料科学中的常用方法,即首先凭借科研工作者的个人经验先对材料的成分、结构、性能等进行设计,然后采用实验手段制备出所设计的材料,再测试其性能,从宏观维度揭示其是否具有应用价值,之后采用表征手段显示其微观形貌特点,解释其内在机理。如果设计的材料不符合预期的特点,则对其进行调整,继续进行上述流程。此种方法需要大量的人力和物力、需要消耗大量的能源、研发周期很长、存在较大的盲目性。随着计算机算力的提升,基于第一性原理的密度泛函理论计算作为材料科学的“第三范式”,被广泛应用于新材料的开发,具有较高的准确性,但此种方法计算花费大[6]。随着人工智能技术的发展,机器学习作为材料科学的“第四范式”,成为材料研发过程的热点,为材料性能的预测[7-9]提供了见解。

铝合金的成分是影响其力学性能的关键因素,Mg、Zn、Cu 是7xxx 系铝合金的主要添加元素,通过影响合金的微观组织变化影响其各项性能[10]。目前商用铝合金的极限抗拉强度均在700 MPa 以下,为了开发工业化高强度7xxx 铝合金,优化合金成分是一种实用的策略[11]。但由于铝合金组成较为复杂,不同组分的铝合金的数量变得难以估量,因此采用传统实验手段进行铝合金的设计变得十分困难。

本文收集了铝合金的组分及抗拉强度值形成初始数据集[11],以铝合金的组分作为输入向量、抗拉强度作为目标向量,采用RF、ET、Bagging、Adaboost建立不同的机器学习算法模型,揭示了铝合金组分性能之间的关系,为铝合金的设计提供理论指导。

1 机器学习算法

1.1 Bagging 算法

Bagging 算法是自举汇聚法(bootstrap aggregating)的简写,是一种并行式的集成学习方法[12],是在自助采样法(Bootstrap Sample)的基础上构建的。自助采样法是指采用随机的、有放回的取样方式,给定m个样本的数据集,随机取出一个样本放入采样集,再把样本放回至初始数据集,重复此过程m轮,则可以得到一个具有m个样本的采样集。重复T次将会产生T个采样集,然后基于每个采样集各训练出一个学习器,最后将这些学习器进行组合从而得到更好的预测结果。在预测输出时,对于分类问题采用简单投票法,对于回归问题采用简单平均法。

1.2 随机森林(RF)

随机森林(Random Forest,RF)是一种以决策树为基学习器的集成学习算法[13],它既可以用于分类问题,又可以用于回归问题。基本思想为将多个弱学习器的结果进行组合,从而形成一个预测性能更好的学习器,即遵循“少数服从多数”的原则。它是Bagging 算法的一种典型的机器学习算法模型。在树的生长过程采用有放回的抽样方式以及采用特征的最佳分割点进行划分,即采用数据随机和特征随机的原则,可以降低学习器的方差,降低模型过拟合的风险。具有鲁棒性强、并行简单、训练速度快等优点。

具体过程如下所述。

1)输入样本集D={(x1,y1),(x2,y2),…,(xm,ym)},对于t=1,2,…,T,对训练集进行第t次随机采样,共采集m次得到包含m个样本的采样集DT。

2)用采样集DT训练第T个决策树模型GT(x)。在结点分裂形成叶子结点时,从所有特征选取一部分特征,对于分类问题,采用最大信息增益、最大基尼增益等方式选取一个最优特征进行决策树左右子树的划分,对于回归问题,采用最小平均绝对误差(MAE),最小均方误差(MSE)的方式进行左右子树的划分。

3)将T个决策树模型组合得到最后的结果。

1.3 极端随机树(ET)

极端随机树(Extremely randomized trees,ET)也是一种集成学习算法[14],既可以用于分类问题,也可以用于回归问题。与随机森林算法类似,都是由许多棵决策树构成的,但是极端随机树并不采取自助采样策略,直接使用原始训练样本,从而可以减少偏差。在每棵决策树的结点分裂时,阈值的选取是随机的。对于回归问题,当样本的特征值大于阈值时分到左分支,小于阈值时,分到右分支,然后计算此时的均方误差或者平均绝对误差。遍历所有的特征值,得到所有特征的均方误差或平均绝对误差。根据误差最大的原则实现对结点的分裂。

1.4 Adaboost 算法

Adaboost 是自适应增强(Adaptive Boosting)的简写,是一种串行式的集成学习算法[15],既可以用于分类问题,又可以用于回归问题。它是由Freund和Schapire 在1995 年提出的[15],其核心思想为提升(boosting)思想,即通过原始数据集生成弱学习器,然后采用迭代的方式更新样本权重生成不同的弱学习器,最后采用结合策略把弱学习器结合起来生成一个强学习器。

具体过程如下所述。

1)初始化样本权重计算式见式(1)。

式中:m为样本的数量;ω1i表示第i个样本的权重;i=1,2,…,m。

2)采用具有权重的样本集进行训练得到弱学习器Gk(x),k=1,2,…,K。

计算弱学习器的回归误差率计算式见式(2)。

式中:ek为弱学习器的回归误差率;m为样本个数;ωki为第k个弱学习器、第i个点的权重;eki为第k个弱学习器、第i个点的相对误差。

相对误差主要有线性误差、平方误差与指数误差3 种,分别如式(3)、(4)、(5)所示。

式中:xi,yi分别为第i个样本点的特征值与目标值。

Ek为最大绝对误差,如式(6)所示。

式中:αk为弱学习器的权重;ek为弱学习器的回归误差率。

4)下一次迭代的权重更新表达式见式(8)～(9)。

式中:Zk是规范化因子,使样本权重和为1;ωki为第k个弱学习器、第i个点的权重;ωk+1,i为第k+1 个弱学习器、第i个点的权重;αk为弱学习器的权重。

5)采用结合策略,构建最终学习器,表达式见式(10)。

式中:f(x)为模型预测值;g(x)是所有αkGk(x)的中位数;αk为弱学习器的权重;k=1,2…,K。

1.5 性能评价指标

不同机器学习算法性能的好坏用平均绝对误差(MAE)和皮尔逊相关系数(R)来评价,分别见式(11)、式(12)。MAE的值越小,R的绝对值越接近于1,表明模型的性能越好。

式中:yi表示铝合金抗拉强度的实验值;表示机器学习算法的预测值;表示铝合金抗拉强度实验值的平均值;表示机器学习算法预测值的平均值。

2 算法建立

材料的结构往往决定着性质,因此材料的组成可能与材料的某种性质存在着线性或者非线性关系。更复杂的材料组成使得其种类成倍增加,因此依靠传统的实验手段获得这些关系变得更加不可能。借助于机器学习算法则使得这个过程变得更加简单,可以揭示这种组分-结构-性质之间的关系。本文所使用的铝合金抗拉强度数据集来源于Li 等人[11]的研究,为实验获得的真实值。以铝合金的6种元素(Zn,Mg,Cu,Y,Ce,Ti)组成作为输入向量,铝合金的抗拉强度作为目标向量,建立不同的机器学习算法模型,基于机器学习的铝合金抗拉强度预测模型构建方法如下所述。

1)数据准备:将73 条数据随机分成两部分,其中以85%的数据作为训练集,用于模型的训练,剩余15%的数据作为测试集,用于评估模型的泛化能力。

2)模型训练:以铝合金元素组成为输入向量,抗拉强度为目标向量,建立Bagging、RF、ET、Adaboost 算法模型,其中Bagging 与Adaboost 均采用决策树(Decision Tree,DT)作为基估计器。

3)模型性能评估:采用平均绝对误差(MAE)、皮尔逊相关系数(R)对模型的性能进行评估。

4)模型解释:采用基于博弈论的SHAP 方法对最好的机器学习算法模型进行解释,探究各个特征对模型性能的影响。

5)模型应用:随机生成不同组分的铝合金,采用最好的模型预测其抗拉强度。

3 结果与讨论

3.1 特征相关性分析

特征与特征之间存在高度的相关性时,会降低模型的稳定性和预测性能,特征与目标向量存在高度的相关性时,则有利于提高模型的稳定性和预测性能。因此首先需要分析特征与特征、特征与目标向量之间的相关性。本文通过特征与特征之间的皮尔逊相关系数热图和mRMR 分数来揭示相关性规律。特征与特征之间的皮尔逊相关系数热图如图1(左)所示,mRMR 分数如图1(右)所示。皮尔逊相关系数是一种衡量相关性的量度,其取值在-1 到1之间,绝对值越接近于1,说明两个特征之间的相关性越高,即存在特征冗余;绝对值越接近0,说明两个特征之间的相关性越低。mRMR(Max Relevance Min Redundancy)[16],即最大相关最小冗余算法,可以通过迭代的方式寻找特征之间相关性最小、与目标向量相关性最大的前k个特征。从图中可以看出,特征之间的相关性很小,mRMR 分数由大到小分别为Ti>Y>Ce>Cu>Mg >Zn,因此特征之间不存在冗余,所以可以直接用于铝合金抗拉强度的预测。

图1 特征相关系数热图(左)及mRMR 分数排名(右)

3.2 不同算法模型预测结果

为了选择出对铝合金抗拉强度预测性能最好的模型,本文采用RF、ET、Bagging、Adaboost 四种机器学习算法建立了铝合金抗拉强度的预测模型,采用皮尔逊相关系数(R)、平均绝对误差(MAE)用于评价模型的性能。皮尔逊相关系数越接近于1,平均绝对误差越小,说明模型的性能越好。图2 显示了不同机器学习算法在训练集与测试集上的表现,它们的皮尔逊相关系数均在0.8 以上,4 种机器学习算法的预测值与真实值均在y=x附近,说明它们都具有很好的预测效果,其中RF 具有最高的皮尔逊相关系数,Adaboost 算法具有最小的平均绝对误差,考虑到RF 的平均绝对误差与Adaboost 相差不大,因此选择RF 算法用于铝合金抗拉强度的预测。

图2 不同算法模型预测结果

3.3 模型解释

类似于RF、ET、Bagging、Adaboost 等的一些非线性的模型尽管在材料性能预测上具有很高的精度,特征的维度相对较高(大于3 维)时,使得模型的解释性下降。模型解释在材料性能预测方面也十分重要,可以使我们探索其中的机理,为新材料的开发提供见解。SHAP(Sharpley Additive explanation)是解决模型可解释性的一种方法,它是Lundberg 和Lee 在2016 年提出的[17]。SHAP 基于Shapley 值,该值是经济学家Lloyd Shapley 提出的博弈论概念。该方法为通过计算在合作中个体的贡献来确定该个体的重要程度。图3 是用于解释RF 模型SHAP 值分布的散点图,我们可以了解每个特征对模型的预测是正向的还是负向的,图中的每一个点代表了每个样本的每个特征对模型输出的贡献,颜色代表了特征值的大小的,红色越深表明特征值越大,蓝色越深表明特征值越小。从图中可以看出,Ti 元素含量对铝合金抗拉强度的预测起正向作用,Ti 元素含量越高,抗拉强度值越大;Mg 元素、Cu 元素含量铝合金抗拉强度的预测作用并不明显;Zn 元素、Ce 元素、Y 元素含量对铝合金抗拉强度的预测起负向作用,即元素含量越大,抗拉强度值越小。图4 显示了RF 模型的SHAP 重要性排序,可以看出,特征重要性从大到小分别为Ti >Mg >Cu >Zn >Ce >Y,Ti 元素含量的特征重要性最大,远远大于其他5 种元素含量,Mg 元素、Cu 元素、Zn 元素含量的特征重要性较为接近,Ce 元素、Y 元素含量的特征重要性较小。

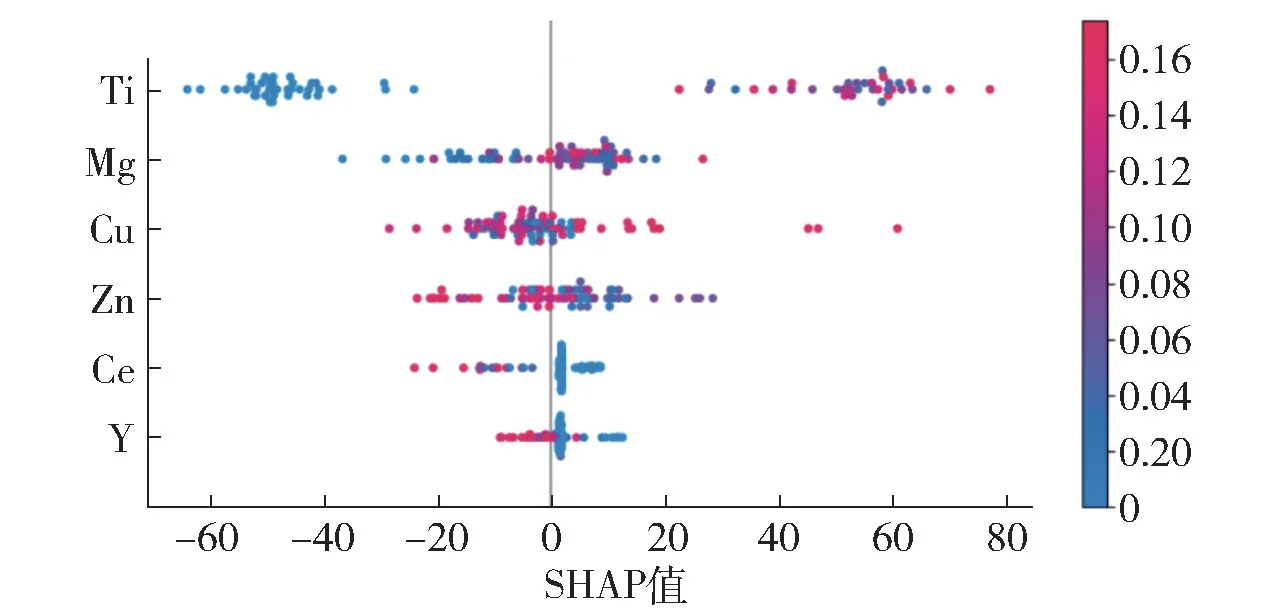
图3 RF 模型SHAP 值分布散点图

图4 RF 模型的SHAP 重要性

3.4 模型应用

在采用铝合金6 种元素组成用于其抗拉强度的预测时,RF 模型拥有最佳的预测效果,它的皮尔逊相关系数为0.89,平均绝对误差为40.33。因此可以随机生成一些虚拟样本,然后通过RF 模型预测其抗拉强度,便于后续通过实验手段进行性能测试,继而为铝合金材料的设计提供见解。表1 显示了原始数据集各元素含量的统计特性,我们可以在各元素含量的最小值、最大值之间生成一些虚拟样本,并采用RF 模型对其抗拉强度进行预测,表2 显示了一些虚拟样本的抗拉强度值。

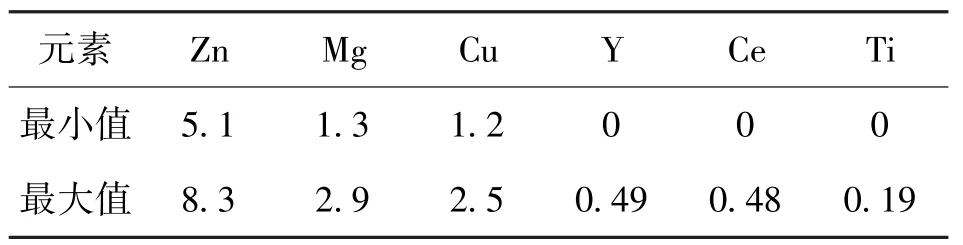
表1 原始数据集各元素含量的统计特性

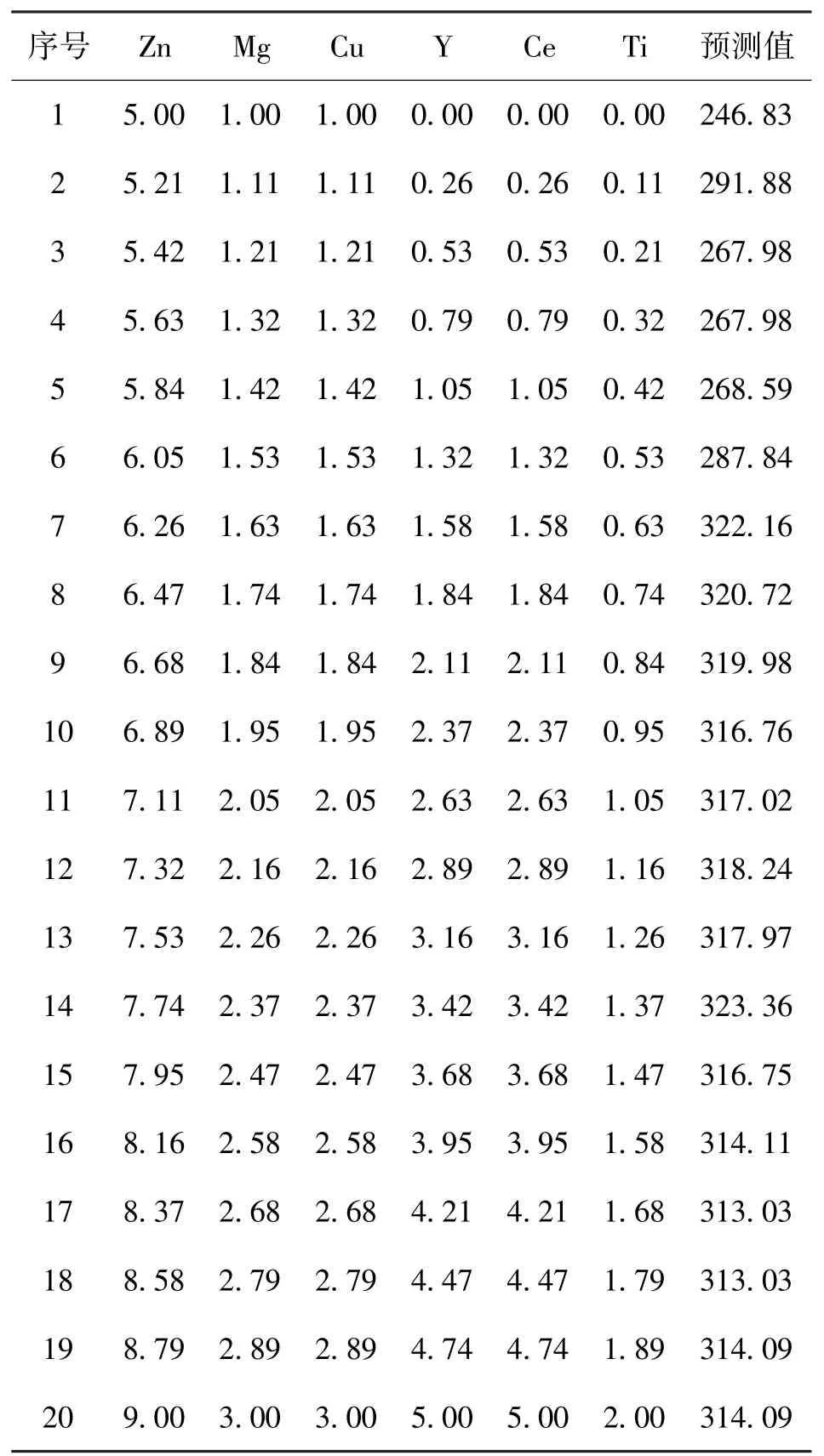
表2 虚拟样本的抗拉强度值

4 结论

1)以铝合金的元素组成为输入向量,抗拉强度为目标变量,采用RF、ET、Bagging、Adaboost 建立了不同的机器学习算法模型,采用皮尔逊相关系数(R)和平均绝对误差对不同机器学习算法模型的性能进行了评价,结果表明:RF 模型具有最佳的预测性能,R=0.89,MAE=40.33。

2)采用基于博弈论的SHAP 方法对RF 模型进行的解释,结果表明:Ti 元素含量对铝合金抗拉强度的预测起正向作用,Ti 元素含量越高,抗拉强度值越大;Mg 元素、Cu 元素含量铝合金抗拉强度的预测作用并不明显;Zn 元素、Ce 元素、Y 元素含量对铝合金抗拉强度的预测起负向作用,即元素含量越大,抗拉强度值越小,特征重要性从大到小分别为Ti>Mg>Cu>Zn>Ce>Y。