基于立体视觉的无人机位姿测量方法

阎峰 刘震

摘 要：现有的无人机位姿视觉测量方法大多基于诸如关键点等几何尺寸在图像和模型间的对应关系完成位姿计算；然而，在复杂情况下易出现关键点图像坐标定位失效的问题，而针对特定机型的算法设计泛化性不佳。针对这一问题，本文提出了一种基于立体视觉的固定翼无人机位姿测量方法，通过立体视觉重建目标无人机三维点云，基于无人机组件三维点云拟合鲁棒地完成位姿测量。首先，使用一种二维、三维数据结合的方式，利用卷积神经网络完成组件的分割。其次，分别利用机翼和机身点云拟合无人机坐标系的z轴和x轴，进而完成目标无人机位姿的计算。整个计算过程无需已知具体机型或尺寸。经试验验证，本文方法在10m的范围内达到了1.57°和0.07m的位姿测量精度，具有较高的精度和鲁棒性。

关键词：机器视觉； 位姿测量； 立体视觉； 无人机； 点云

中图分类号：V249 文献标识码：A DOI：10.19452/j.issn1007-5453.2023.04.010

基金项目： 航空科学基金（201946051001）

无人机技术具有覆盖范围大、灵活性高及可代替人工执行危险工作等优点，在各行业、各领域内发挥着日益重要的作用。无人机功能[1-2]的实现主要依靠编队工作的方式，而编队功能的有效实现，依赖于无人机间相对位姿的准确测量。因此，实现无人机位姿的精准测量具有重要意义。

视觉测量具有非接触、精度高和灵活性好等优势，近年来在位姿测量领域得到了较为广泛的研究和应用。相比通过惯性器件测量位姿的方式[3]，视觉测量不存在累计误差，且不依赖于无人机之间的通信，具有更强的灵活性和自主性。因此，研究一种无人机位姿测量的视觉方案对该领域的发展具有重要推动作用。

目前，无人机位姿的视觉测量方案大多需要已知精确的几何尺寸作为先验信息，如需要明确具体的机型、在模型坐标系下关键点的三维坐标等，按照模型的使用方式不同，大致可将现有算法分为三类：第一类是PnP类算法，PnP是Perspective-n-Point的简写，这类算法需定义多个关键点，基于提取得到的关键点二维图像坐标和其先验的三维世界坐标的对应关系，完成无人机位姿的计算。这类算法灵活、快速，最早由M. A. Fischler[4]提出，后续涌现了大量的改进算法。其中较为经典的为EPnP算法[5]，通过设置4个虚拟控制点，可高效求解目标位姿。除了关键特征点，特征边缘也可用于这类计算。Ji Bing[6]使用角点和边缘等多个特征，共同计算飞机位姿，以解决特征点易被自身遮挡的问题。尽管如此，这类算法由于使用的都是稀疏特征，在复杂条件下，如目标较远或成像质量较差等情况下，这类特征易被噪声淹没，以至于难以准确甚至无法完成图像特征的提取，进而导致算法失效。第二类是模板匹配算法[7]，这类算法需要实现根据所需测量的模型制作包含大量不同位姿的模板库，然后将提取得到的目标图像与模板库进行匹配，找到对应的位姿。这类方法只能针对特定的某一机型完成测量，且模板库的制作过程烦琐，算法的泛用性较差。第三类是机器学习与深度学习方法，这类算法是指首先使用待测目标的数据集训练分类器或者神经网络，完成训练后，使用得到的权重进行位姿的回归计算。J. Liebelt[8]提出了一种SVM分类器与RANSAC算法结合的方法，实现对三维目标的位姿测量。李想[9]使用RGB图像并利用卷积神经网络（CNN）方法完成对目标位姿的测量。此方法计算直接，且通常具有较高精度；但是与模板匹配方法类似，也需要事先针对所处理机型制作大量数据集，较为繁琐。另外，使用深度学习方法直接进行位姿计算，网络规模通常较大，需要大量计算资源，不适合在机载环境中使用。

综上所述，现有的无人机位姿视觉测量算法大多需要先验的精确几何尺寸，关键点或边缘虽然精准，但是由于其较为稀疏，所以易被噪声淹没。另外，固定翼无人机多采用大展弦比柔性机翼，飞行时机翼易变形，导致特征点位置发生移动，进而导致算法失效；使用特定机型作为模型则使用了较多的个性特征，这将导致算法不鲁棒或泛用性较差。基于上述分析，如能使用稠密数据，基于共性结构完成无人机位姿的计算，将大大缓解现有算法存在的问题，提升算法的鲁棒性和泛用性。

基于这一想法，本文提出了一种基于立体视觉的无人机位姿视觉测量算法，使用立体视觉重建目标无人机三维点云，通过拟合无人机机身、机翼等组件的三维点云数据，完成位姿的测量。三维点云属于稠密数据，在复杂条件下仍能为算法提供大量的信息源，且局部发生变形时，整体仍能保持相对稳定，具有较强的魯棒性；而固定翼无人机基本都是由机身、机翼以及垂尾等组件组成，算法不依赖于某一具体机型，具有较强的泛用性，可以解决现有算法存在的问题。

1 二维、三维数据获取方法

本文采用双目立体视觉传感器实现二维数据和三维数据的采集，其中，二维数据是指视觉传感器拍摄得到的图像数据，三维数据是指通过立体匹配算法得到的视差图、深度图和三维点云数据。具体的数据获取算法如下。

1.1 双目立体视觉传感器测量模型及标定

标定是测量的前提，只有已知上述提及的内部参数和结构参数，才可基于图像特征完成三维信息的解算。本文采用张正友方法[10]完成双目立体视觉传感器内部参数和结构参数的标定。

1.2 视差匹配与三维重建

由于是由二维图像数据匹配得到，使用双目立体视觉传感器重建得到的三维点云数据具有与二维数据的同源性，即点云中的每一个元素都与二维图像中的像素一一对应。这为后续点云分割提供了较为便利的条件。

2 无人机位姿视觉测量算法

本文所提出的无人机位姿测量算法无需已知几何尺寸，使用机身、机翼等固定翼无人机通用组件点云拟合完成位姿计算。基于双目立体视觉传感器获得的二维、三维数据，首先完成无人机组件点云的分割；然后基于分割结果，使用无人机组件点云拟合坐标系，完成无人机位姿的计算。具体算法介绍如下。

2.1 无人机组件点云拟合

无人机机体坐标系op-xpypzp的常见的定义方式如图2所示，取机身纵轴为x轴，指向前方；y轴垂直于对称面指向右方；z轴在对称面内垂直于纵轴并指向下方。本文中，将机体坐标系的原点定义在机身中心位置。根据坐标系定义，机身中轴方向为无人机坐标系的x轴方向，机翼法线方向为无人机坐标系的z轴方向。基于这一思想，可首先完成点云分割，然后使用点云拟合的方式完成无人机坐标系的计算。

本文采用深度学习的方式完成点云分割。由于直接分割三维点云计算量过大、计算速度慢，因此，本文利用双目立体视觉传感器获取二维、三维数据的同源性，首先完成二维图像的分割，然后映射至点云空间，完成无人机组件的三维点云分割。具体而言，本文采用了一种如图3所示的编解码结构的RGB-D卷积神经网络，综合RGB图像的纹理信息和深度图像的空间信息，深度图像可通过匹配获得。在编码阶段分为RGB图和深度图两个通道，首先通过残差卷积单元（RCU）模块[12]分别提取图像特征，然后使用空洞空间金字塔池化（ASPP）模块[13]实现多尺度目标的感知，最后使用残差卷积融合（RCF）模块将RGB通道特征和深度图特征进行融合。在解码阶段，使用残差语义引导融合（RSGF）模块在低层特征的指导下逐层恢复空间信息，完成二维图像的分割。其中，RCF和RSGF模块都是本文提出的网络模块，其结构如图4所示。网络设计中使用了大量的残差连接，提升了网络的恒等性，加速网络收敛，提升网络性能。完成图像分割后，将分割结果映射至点云空间，完成组件的点云分割。

獲得各组件点云后，可分别对机翼和机身点云进行拟合，获得无人机坐标系各轴矢量。

2.2 无人机位姿求解

一般认为机翼的中轴线穿过机身中心，因此，可取机翼中轴线与机身xp轴交点作为无人机坐标系的原点，该点坐标即为无人机的位置参数。

3 试验验证

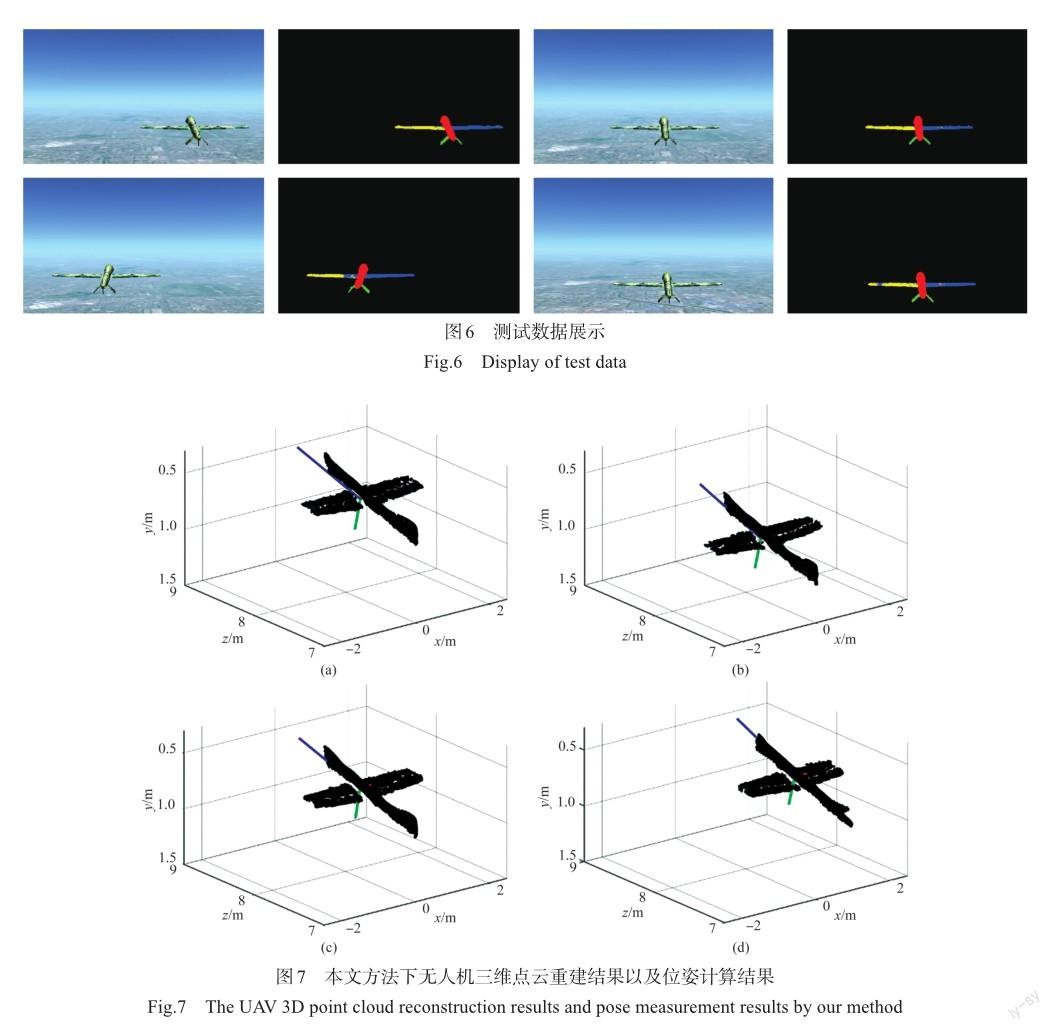
本文采用数字仿真的方式对算法的有效性进行分析验证。本文使用一款视景仿真软件，生成机载条件下的双目立体视觉传感器成像。在试验过程中，所测量的无人机机型为Predator型无人机。在试验过程中，传感器参数见表1。试验过程中，数据处理流程如下：首先使用SGBM算法完成左右图像的匹配，得到深度图像和三维点云数据。在试验前，使用1978张无人机图像组成数据集，完成了神经网络的训练；训练过程中使用的无人机图像为本文制作完成，包含不同位置和姿态的Predator型无人机图像，并通过手工标注完成组件分割真值的获取，数据集部分图像如图5所示。数据集中不同图像中的无人机分别处于视场中的不同位置和深度，呈现出不同的视角；分别以不同的角度进行飞行，呈现出不同的姿态。训练后，分割网络达到了82.11%的平均交并比[12]，达到了较高精度。在试验过程中，使用RGB图像和深度图像并使用网络完成对目标无人机机身、机翼等组件的分割，分割完成后将其映射至点云空间，完成对三维点云的分割。最后，使用分割得到的点云组件进行坐标系的拟合，计算目标无人机位姿。本文共使用了40张图像进行测试，根据飞行阶段的不同，将其划分为5个组别。图6展示了部分测试图像及其分割结果，可以发现，分割达到了较高精度，能够准确识别无人机的各个组件。

试验主要从两个方面展开分析：（1）本文算法精度分析；（2）不同特征形式在机载复杂条件下的鲁棒性对比分析。

3.1 本文方法精度分析

本节首先通过本文算法计算结果同真值进行对比，通过计算各轴分量均方根误差（RMSE）测试分析本文算法的精度。

用于测试无人机数据根据飞行位置不同可以分为5个阶段，本节使用本文方法分别计算所有测试图像的位姿数据，通过将其与真值对比并统计各阶段以及总体的RMSE对算法的精度进行评价。

试验结果分别如图7、图8所示。其中，图7展示了各阶段中具有代表性的4个位置的三维稠密点云重建结果，从图中可以看出，本文算法能够较高精度地完成无人机稠密点云的重建，并能够准确地计算位姿。图中蓝色、红色以及绿色分别代表无人机坐标系的x轴、 y轴及z轴。

图8展示了各阶段位姿计算结果的RMSE值，并将其绘制成曲线。从图中可以看出，本文方法姿态测量误差基本小于3°，其中x轴姿态测量误差基本小于1°；本文方法位置测量误差基本小于0.12m；不同阶段的测量结果表现较为稳定。经统计，在10m范围内，本文方法姿态测量总均方根误差为1.57°，位置测量总均方根误差为0.07m，达到了较高精度。

3.2 本文算法与经典算法的对比分析

PnP算法使用单目相机获取的多对二维图像特征点与对应三维坐标求解目标位姿，是较为经典的位姿测量方法。因此在分析本文算法精度的基础上，本节将本文算法同PnP及其改进算法EPnP进行对比，分析位姿测量的鲁棒性。

本文选取机翼及垂尾处较为显著的7个角点作为关键点，使用PnP及EPnP算法计算位姿。统计40张测试图片的位姿测量RMSE可得，在10m的范围内，EPnP的姿态测量精度为5.07°，位置测量精度为0.07m；PnP的姿态测量精度为2.38°，位置测量精度为1.47m；本文算法的姿态测量精度为1.57°，位置测量精度为0.07m。图9展示了不同方法的位姿测量结果。

如图9所示，图中红色坐标系为本文方法计算结果、蓝色坐标系为EPnP方法计算结果、绿色坐标系为PnP方法计算结果，其中由于PnP算法在机载复杂条件下位姿计算精度一般，其坐标系在投影后未出现在视场中。从图中可以发现，本文方法在不同位置姿态下各参数计算精度均较高，而EPnP算法虽然可以较为准确地估计无人机的位置，但是其姿态解算精度一般。这说明PnP及EPnP算法易受特征点数量及分布影响，位姿测量精度一般；而本文算法所基于的空间几何特征是由稠密三维点云拟合得到的，在不同位置、不同姿态情况下均能鲁棒提取，基于该特征可以精确地计算位姿参数，证明了本文算法的鲁棒性。

4 结论

本文提出了一种基于立体视觉的无人机位姿视觉测量算法，通过立体视觉重建目标无人机三维点云，使用固定翼无人机共有的机身和机翼点云拟合无人机坐标系，完成位姿计算。算法无须已知精确的几何尺寸，是面向固定翼无人机的通用算法，具有较强的泛用性；同时，位姿测量使用的是点云拟合的方式，数据来源广、精度高、鲁棒性强。经试验测试，本文算法达到了10m内1.57°的姿态精度和0.07m的位置精度，在复杂条件下仍能稳定测量，具有较高精度和鲁棒性，可实现在中近距离下空中飞行或地面停靠状态下无人机位姿的精准测量。

参考文献

[1]贾汉博，马琳，张忠旺.基于POA算法的无人机航跡规划优化方法[J].航空科学技术，2022，33（10）：96-102. Jia Hanbo， Ma Lin， Zhang Zhongwang. Optimization method of unmanned aerial vehicle path planning using POA[J]. Aeronautical Science & Technology， 2022， 33（10）： 96-102.（in Chinese）

[2]张炯，牛欢，陈雪.基于多传感器融合的无人机应急着陆功能研究[J].航空科学技术，2022，33（11）：11-20. Zhang Jiong， Niu Huan， Chen Xue. Research on UAV emergency landing function based on multi-sensor fusion [J]. Aeronautical Science & Technology， 2022， 33（11）： 11-20. （in Chinese）

[3]Oh T J， Chung M J. Global pose estimation with adaptive GPS/ IMU fusion[C]//Intelligent Autonomous Systems 12th. Poland： Springer， 2013：613-620.

[4]Fischler M A， Bolles R C. Random sample consensus： A paradigm for model fitting with applications to image analysis and automated cartography[J]. Readings in Computer Vision， 1987，15：726-740.

[5]Lepetit V， Moreno-Noguer F， Fua P. EPnP： An accurate solution to the PnP problem[J]. International Journal of Computer Vision， 2009， 81（2）：155-166.

[6]Ji Bing， Shan Ganlin， Zhou Yunfeng， et al. Aircraft pose estimation based on integrated feature matching[C]// IEEE Conference on Industrial Electronics & Applications. IEEE， 2009： 226-229.

[7]赵正川. 基于高速视频的目标状态识别技术研究[D]. 西安：西安工业大学，2016. Zhao Zhengchuan. The research of target state recognition technology based on high-speed video [D]. Xi’an： Xi’an Technological University， 2016.（in Chinese）

[8]Liebelt J， Schmid C， Schertler K. Viewpoint-independent object class detection using 3D feature maps [C]// IEEE Conference on Computer Vision and Pattern Recognition（CVPR）， IEEE， 2008： 2118-2125.

[9]李想. 基于深度學习的空间非合作目标姿态估计算法设计[D]. 哈尔滨：哈尔滨工业大学，2018. Li Xiang. Design of attitude estimation algorithm for space non-cooperative targets based on deep learning [D]. Harbin： Harbin Institute of Technology， 2018.（in Chinese）

[10]Zhang Zhengyou. A flexible new technique for camera calibration[J]. IEEE Trans. Pattern Analysis and Machine Intelligence， 2000， 22（11）， 1330-1334.

[11]Hirschmuller H. Stereo processing by semiglobal matching and mutual information[J]. IEEE Transaction. Pattern Analysis and Machine Intelligence， 2007， 30（2）： 328-341.

[12]Lin Guosheng， Milan A， Shen Chunhua， et al. RefineNet： Multi-path refinement networks for high-resolution semantic segmentation[C]// IEEE Conference on Computer Vision and Pattern Recognition （CVPR）. IEEE， 2017： 1925-1934.

[13]Chen L C， Papandreou G， Schroff F， et al. Rethinking atrous convolution for semantic image segmentation [EB/OL].（2017-12-05）. https：//arxiv.org/abs/1706.05587.

[14]Torr P H S， Zisserman A. MLESAC： A new robust estimator with application to estimating image geometry [J]. Computer Vision and Image Understanding， 2000， 18（1）：138-156.

UAV Pose Measurement Method Based on Stereo Vision

Yan Feng， Liu Zhen

Key Laboratory of Precision Opto-mechatronics Technology， Ministry of Education，Beihang University， Beijing 100191， China

Abstract： Most of the existing UAV pose visual measurement methods are based on the corresponding relationship between the image and the model of geometric size such as key points. However， the problem of detection failure of key point image coordinate is easy to occur in complex cases， and the algorithm designed for specific models has poor generalization. To solve this problem， this paper proposes a pose measurement method of fixed wing UAV based on stereo vision. 3D point cloud of target UAV is reconstructed through stereo vision， and the pose measurement is completed robustly based on the 3D point cloud fitting of UAV components. Firstly， the components are segmented by a convolutional neural network in a 2D and 3D data combination fashion， and then the wing and fuselage point cloud are used to fit the z axis and x axis of the UAV coordinate system， and then the pose of the target UAV is calculated. The whole calculation process does not need to know the specific model or size. The experimental results show that the proposed method can reach the accuracy of 1.57° and 0.07m in the range of 10m， which shows high accuracy and robustness.

Key Words： machine vision； pose measurement； stereo vision； UAV； point cloud