分布式旋翼飞行器耦合动特性参数影响研究

张贵宝 程起有 王司文 孙凤楠

摘 要：为探索不同参数对分布式旋翼飞行器动特性的影响机制，采用Hamilton原理和中等变形梁理论推导了分布式旋翼/短舱/机翼耦合结构动力学方程，建立了适用于耦合动特性分析的求解方法，计算了旋翼/短舱/机翼耦合模态，结果对比误差小于5%，表明本文建立的计算方法是准确有效的。在此基础上研究了旋翼线密度、短舱高度、旋翼转速、安装位置参数对耦合动特性的影响，得出一些结论规律：分布式旋翼飞行器的短舱长度增加时，机翼模态将整体减小；旋翼、机翼模态频率同时受到旋翼线密度的影响；分布式旋翼安装位置向翼尖移动时，机翼扭转频率明显变小。本文结论可为分布式旋翼飞行器设计提供参考。

关键词：分布式； 多旋翼飞行器； 动特性； 参数影响

中图分类号：V275.1 文献标识码：A DOI：10.19452/j.issn1007-5453.2023.04.006

分布式旋翼飞行器是一款利用分布式概念的新型旋翼飞行器[1-4]，其机翼采用大展弦比设计，使得机翼的结构柔性增加，同时分布式多旋翼构型布局，使得每个部件的刚度、惯量等都可能会影响耦合动力学特性，因此研究分布式旋翼飞行器耦合动特性机理、分析耦合动特性影响规律对于分布式旋翼飞行器的设计是有必要的。

对于分布式旋翼飞行器和与其相似构型飞行器的动力学特性，H. K. Edenborough[5]进行了XV-3倾转旋翼机的全尺寸模型的风洞试验研究，结果表明改变短舱的支撑刚度，會影响耦合系统的动特性，适当提高短舱刚度可以提高系统稳定性。A. Cravana[6]分析了弹性机翼、发动机、螺旋桨不同配置下的影响，通过调整发动机位置和旋转螺旋桨，分析机翼模态频率的变化趋势，结果表明载荷分布和展向位置对机翼的扭转和摆振频率有显著影响。C. B. Hoover等[7-10]对美国国家航空航天局（NASA）分布式电动飞机X-57的半翼展模型和全尺寸模型进行了研究，结果表明，调整桨叶刚度或桨叶上的翼型分布会使机翼阻尼比发生明显变化，同时机翼刚度的改变会影响各阶模态的频率和阻尼比。国内谢长川等[11-13]对大展弦比机翼的建模进行了研究，分析了几何非线性因素对大展弦比机翼的影响，结果表明几何非线性会导致结构固有频率与振型的改变，从而影响结构的动力学特性。陈兆林等[14]研究了常规机翼结构参数的影响，结果表明，机翼结构的弹性对螺旋桨发动机俯仰模态频率影响很大，对偏航模态频率影响较小，这会改变两种模态频率之差，影响机翼螺旋桨模态耦合的程度。对于分布式旋翼飞行器，国内还处于探索研究阶段，与动力学相关的直接研究资料较少。

本文针对分布式旋翼飞行器，建立适用于分布式旋翼飞行器的构型动力学方程以及耦合动特性求解方法，研究旋翼线密度、短舱高度、旋翼转速、安装位置对分布式旋翼飞行器动特性的影响。

1 建模与分析方法

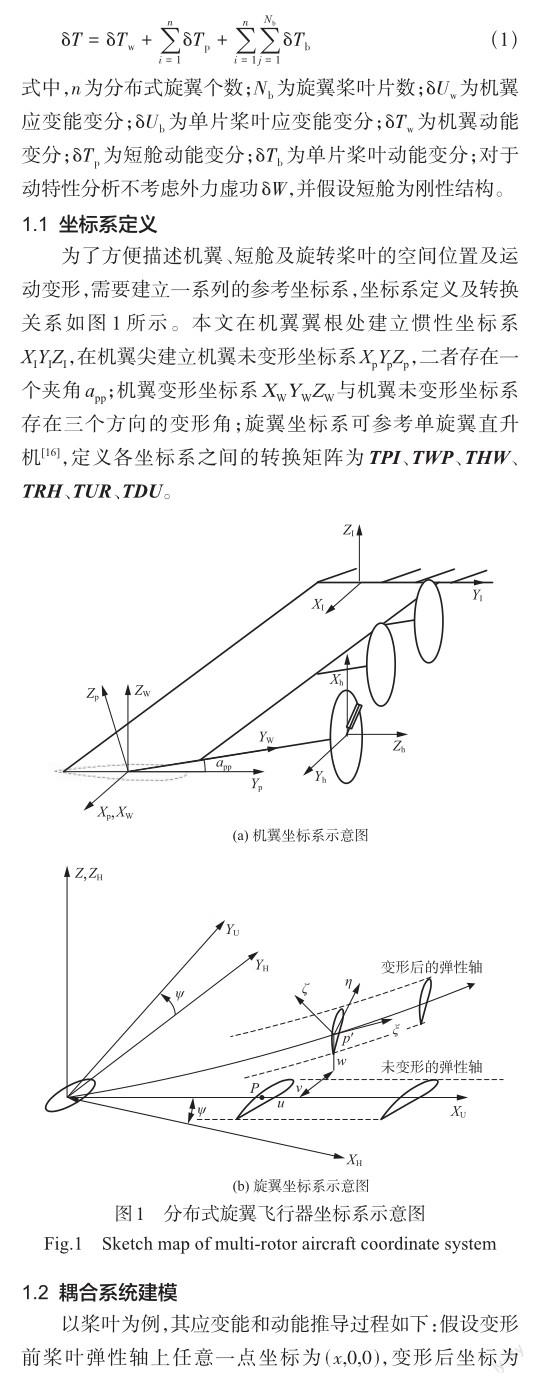
2 算例验证

针对分布式旋翼飞行器的动特性计算，本文设计了一个半展旋翼/短舱/机翼耦合模型（见图2）作为计算输入，基本参数见表1，其中各类参数为无量纲化参数，与参考值进行对比验证，结果见表2。

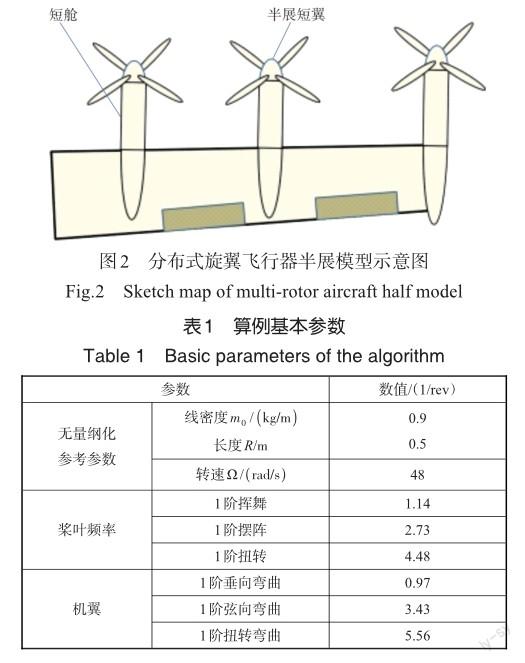
计算结果相对误差都在5%以内，说明本文旋翼/机翼耦合结构理论模型是准确的。

3 分布式旋翼飞行器参数影响分析

对于耦合模态识别，可借助耦合振型示意图（见图3）和旋翼频率特点（集合、周期、无反作用型频率加减ΩK关系）共同识别，以提高识别准确度。

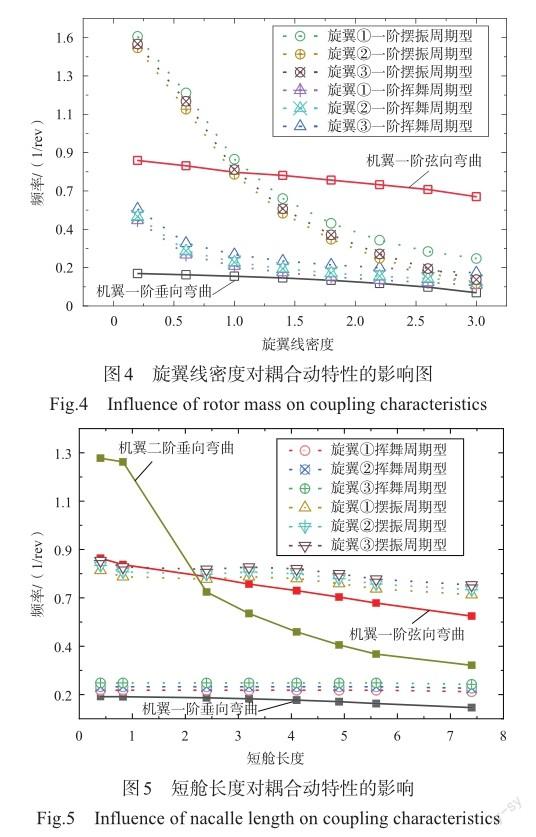
图4为旋翼线密度对旋翼机翼耦合动特性的影响曲线图。从图4可见，随着旋翼线密度增大，旋翼、机翼频率均在减小，其中旋翼摆振频率降幅最大达85%；当线密度增加到3附近时，旋翼挥舞、摆振频率与机翼垂向弯曲频率靠近，存在耦合共振风险。增大旋翼线密度，旋翼、机翼频率同时减小，分析原因是旋翼线密度增加，旋翼质量增大，从频率定义可知，质量增大，频率自然减小；机翼频率也在减小，原因可能是旋翼机翼耦合时，机翼质量矩阵附加上了旋翼质量。

图5为短舱长度对耦合动特性的影响曲线图。从图5可见，随着短舱长度增加，机翼频率整体减小，其中机翼二阶垂向弯曲频率明显减小；旋翼频率中，1阶摆振周期型频率略有减小，1阶挥舞周期型频率基本不受影响。增加短舱长度，机翼频率整体减小，是因为短舱长度增加对于机翼来说相当于增加附加质量，故机翼频率整体减小；旋翼1阶摆振周期型频率减小，可能是短舱长度增加对于旋翼来说相当于减弱支撑刚度，因此旋翼频率也在减小。

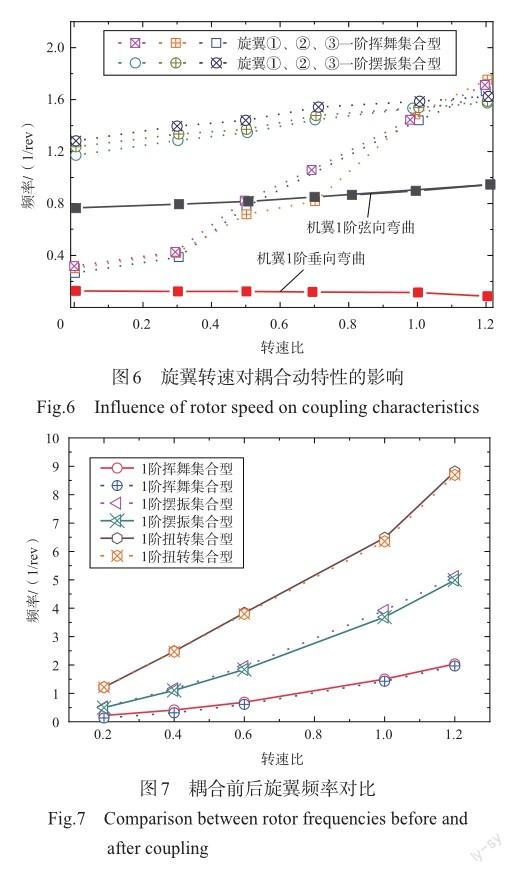
为了分析旋翼转速的影响，设定三副旋翼转速相同，转速比在0～1.2范围内变化，其参数影响曲线如图6所示。从图6可见，增加旋翼转速，旋翼频率普遍增大，其中旋翼一阶挥舞频率明显增加，增幅最大达到85%；机翼变化相对较小，其中机翼一阶弦向弯曲频率略有增加，一阶垂向弯曲频率略有减小。进一步绘制旋翼耦合前后频率对比曲线图，如图7所示，其中虚线代表未耦合时旋翼频率随转速的变化，实线代表耦合后旋翼频率随转速的变化。从图7可见，耦合前后曲线（实线与虚线）基本重合，说明改变转速，旋翼/机翼耦合对于旋翼频率影响不大。

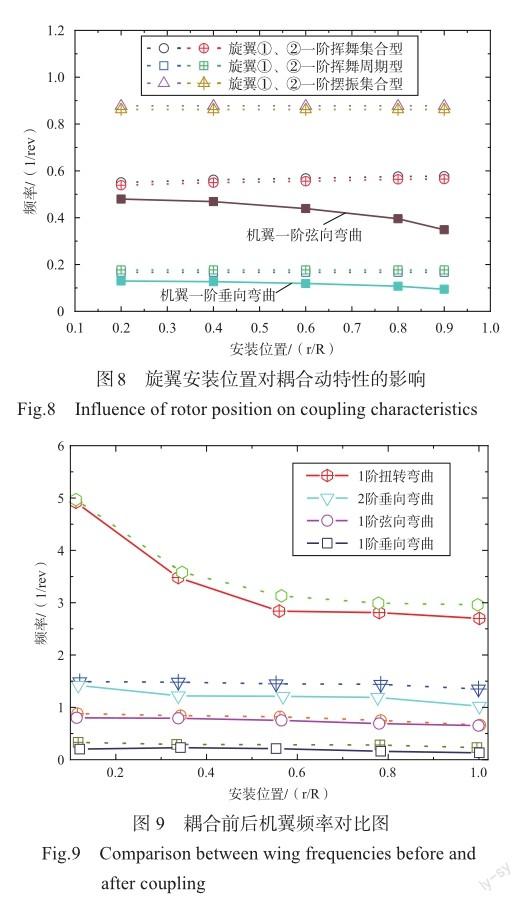
对分布式旋翼安装位置进行分析时，为了便于控制单一变量影响，布置两副旋翼，旋翼①固定在机翼翼尖，旋翼②在0.2～0.9范围内移动，并在图8、图9中绘制分布式旋翼安装位置对耦合动特性的影响曲线。

从图8可见，随着旋翼②向机翼翼尖移动，机翼1阶弦向弯曲与1阶垂向弯曲频率呈减小趋势；旋翼一阶摆振集合型与一阶挥舞周期性频率基本不受影响，一阶挥舞集合型频率有上升趋势。为分析旋翼/机翼耦合对机翼频率的影响，在图9中绘制耦合前后机翼频率变化曲线，虚线为未耦合时机翼频率，实线为耦合后机翼频率。从图9可见，旋翼②在0.2～0.6范围移动，机翼的1阶扭转频率明显下降，0.6～1.0范围移动扭转频率趋于平缓；耦合后机翼频率（实线）与未耦合机翼频率（虚线）对比，耦合后频率曲线均低于未耦合频率曲线。在0.2～0.6范围机翼扭转频率明显减小，分析原因可能是安装位置向翼尖靠近时，会大大提高机翼扭转惯量，从而使机翼扭转频率明显降低；0.6～1.0范围内扭转频率趋于平缓，可能是旋翼安装位置向翼尖靠近时增大了机翼挥、摆、扭之间耦合，扭转频率受挥舞与摆振的影响，因此变化变缓。

4 结论

本文采用Hamilton原理和中等变形梁理论，建立了适用于分布式旋翼飞行器耦合动特性分析的求解方法，计算分析了旋翼、机翼典型频率和振型，绘制相应参数影响曲线，得到以下结论：

（1） 改变分布式旋翼飞行器的短舱长度主要影响机翼模态，对旋翼影响有限；短舱长度增加，机翼频率整体减小，旋翼频率中，1阶摆振周期型频率略有减小，1阶挥舞周期型频率基本不受影响。

（2） 旋翼转速主要影响旋翼模态，转速增加，旋翼频率普遍增大；改变旋翼线密度，旋翼、机翼频率同时受到影响，旋翼线密度增大，旋翼、机翼频率均会减小。

（3） 改变分布式旋翼飞行器的旋翼安装位置，机翼模态受影响较大；短舱长度增加，机翼频率普遍降低；当旋翼安装位置向翼尖移动时，机翼扭转频率变化明显。

参考文献

[1]李開省.电动飞机核心技术研究综述[J].航空科学技术，2019，30（11）：8-17. Li Kaisheng. Electric aircraft core technology research review[J]. Aeronautical Science & Technology， 2019， 30（11）： 8-17. （in Chinese）

[2]王妙香.NASA亚声速大型飞机电推进技术研究综述[J].航空科学技术，2019，30（11）：22-29. Wang Miaoxiang. NASA subsonic large aircraft electric propulsion technology research review[J]. Aeronautical Science & Technology， 2019，30（11）：22-29. （in Chinese）

[3]Dikyar S. Nonlinear control of a quad tilt-wing UAV[D]. Sabanc？ University， 2011.

[4]朱炳杰，杨希祥，宗建安，等.分布式混合电推进飞行器技术[J].航空学报，2022，43（7）：48-64. Zhu Bingjie，Yang Xixiang，Zong Jian’an，et al. Distributed hybrid electric propulsion vehicle technology[J]. Acta Aeronautica et Astronautica Sinica，2022，43（7）：48-64.（in Chinese）

[5]Edenborough H K. Investigation of tilt-rotor vtol aircraft rotorpylon stability[J]. Journal of Aircraft， 1968， 5（2）： 97-105.

[6]Cravana A，Manfreda G，Cestino E， et al. Aeroelastic behaviour of flexible wings carrying distributed electric propulsion systems[R]. Sae Technical Paper， 2017.

[7]Hoover C B，Shen J，Kreshock A R， et al. Whirl flutter stability and its influence on the design of the distributed electric propeller aircraft X-57[C]//17th AIAA Aviation Technology， Integration， and Operations Conference， 2017： 3785.

[8]Hoover C B， Shen J， Kreshock A R. Propeller whirl flutter stability and its influence on X-57 aircraft design[J]. Journal of Aircraft， 2018， 55（5）： 2169-2175.

[9]Hoover C B，Shen J. Parametric study of propeller whirl flutter stability with full-span model of X-57 maxwell aircraft[J]. Journal of Aircraft， 2018， 55（6）： 2530-2537.

[10]Hoover C B，Shen J. Parametric study of whirl flutter stability of the NASA aircraft X-57[C]//2018 AIAA Aerospace Sciences Meeting， 2018： 276.

[11]杨超，杨澜，谢长川.大展弦比柔性机翼气动弹性分析中的气动力方法研究进展[J].空气动力学学报，2018，36（6）：1009-1018+983. Yang Chao， Yang Lan， Xie Changchuan. Advances in aerody‐namic methods for aeroelastic analysis of flexible airfoils with large span-to-chord ratio[J]. Acta Aerodynamica Sinica，2018，36（6）：1009-1018+983.（in Chinese）

[12]谢长川，张利娟，刘燚，等.螺旋桨/大柔性机翼静气动弹性快速分析方法[J].北京航空航天大学学报，2015，41（1）：147-153. Xie Changchuan， Zhang Lijuan， Liu Yan， et al. Rapid analysis method for propeller/large flexible airfoil static aeroelasticity[J]. Journal of Beijing University of Aeronautics and Astronautics， 2015，41（1）：147-153.（in Chinese）

[13]谢长川，杨超.大展弦比飞机几何非线性气动弹性稳定性的线性化方法[J].中国科学：技术科学，2011，41（3）：385-393. Xie Changchuan， Yang Chao. Linearization method for geometrically nonlinear aeroelastic stability of aircraft with large spreading chord ratio[J]. Scientia Sinica Techologica， 2011，41（3）：385-393.（in Chinese）

[14]陈兆林，杨智春，谷迎松.机翼对螺旋桨发动机旋转颤振的影响研究[J].航空学报，2016，37（11）：3351-3360. Chen Zhaolin， Yang Zhichun， Gu Yingsong. Study on the effect of wing on rotational chatter of propeller engine[J]. Acta Aeronauti‐ca et Astronautica Sinica， 2016，37（11）：3351-3360.（in Chinese）

[15]黃昭度，纪辉玉.分析力学[M].北京：清华大学出版社，1985. Huang Zhaodu， Ji Huiyu. Analytical mechanics[M]. Beijing： Tsinghua University Press，1985.（in Chinese）

[16]周薇.直升机旋翼/机身耦合气弹响应及分岔问题研究[D].南京：南京航空航天大学，2014. Zhou Wei. Helicopter rotor/fuselage coupled air-elastic response and bifurcation problem study[D]. Nanjing： Nanjing University of Aeronautics and Astronautics，2014.（in Chinese）

[17]Gunjit B. Multi-blade coordinate transfor-mation and its application to wind turbine analysis[C]//46th AIAA Aerospace Science Meeting and Exhibit， 2008.

Study on Coupling Dynamic Characteristics and Parameter Influence of Multi-tiltrotor Aircraft

Zhang Guibao， Cheng Qiyou， Wang Siwen， Sun Fengnan

Science & Technology on Rotorcraft Aeromechanics Laboratory， China Helicopter Research and Development Institute， Jingdezhen 333001， China

Abstract： In order to explore the influence mechanism of different parameters on multi-rotor aircraft dynamic characteristics，Hamilton principle and the theory of medium deformation beam are used to derive the rotors/nacelle/ wing coupling structure dynamic equation， and a solution method suitable for the analysis of coupled dynamic characteristics is established.By using literature as an example calculate rotor/ nacelle /wing coupling frequency，the error is less than 5% compared with the experimental results in the literature，indicating that the coupling model in this paper is accurate and effective.On this basis，the influences of rotor mass，nacelle length，rotor speed，spanwise position on the coupling dynamic characteristics are studied， the typical frequencies and vibration patterns of rotor and wing are calculated and analyzed， the respective parameter influence curves are drawn， and some meaningful conclusions and parameter influence laws are obtained， which provides reference for the design of distributed rotorcraft.

Key Words： distributed； multi-rotor aircraft； dynamic characteristic； parameter influence