共轨飞行航天器轨道特性分析
张相宇 田百义 汪中生
(北京空间飞行器总体设计部,北京 100094)
随着我国空间站的全面建成,一种新的与空间站保持长期共轨飞行,在必要时可与空间站交会对接进行燃料补给、维修和设备更新换代的飞行模式被提了出来[1]。这种模式既不对空间站的主任务造成影响,还将空间站视为在轨服务平台从而扩展了空间站的应用范围。共轨飞行期间空间站按照自身的任务目标进行轨道维持,共轨飞行航天器以空间站轨道为基准进行相对轨道控制,平时在距离空间站一定的相位范围内自主独立飞行,对空间站的轨道无任何约束,需要维护时通过远程导引、近程导引与空间站实现交会对接。为了保证在任何时刻以较小的代价且较快实现与空间站的交会对接,需要将共轨飞行航天器的轨道限制在相对空间站轨道面内、面外一定范围[2-4]。这种飞行模式既不同于现有编队飞行任务中将多颗卫星作为一个整体进行轨道控制[5];也不同于对航天器的近距离绕飞、伴飞任务,其辅星采用基于C-W方程的相对运动控制[6]。
共轨飞行可扩展为两在轨飞行航天器的长期近共面飞行问题。文献[2]针对载人航天任务中与空间站保持长期共轨飞行的轨道问题,分析了航天器在J2项摄动、大气阻力摄动和轨道机动下,升交点赤经和相位的相对变化,但并没有给出两者之间的直接关系,仅给出了一种控制策略和误差的仿真算例,并未从解析的角度分析误差的演化关系。文献[3]以与空间站共轨飞行的光学舱补给燃料为背景,基于虚拟共面的思想提出了一种减小轨道面外冲量的共轨飞行器位置部署方法,得到的相位与升交点赤经部署关系的相对误差小于3%,但该方法没有考虑大气阻力和轨道机动的影响。文献[7]针对小卫星与共轨目标星之间的交会问题,基于相对运动模型采用Lambert算法设计了制导策略使小卫星在固定时间内与目标星相遇,但未给出共轨飞行期间的轨道参数关系。文献[8]应用GNSS数据拟合卫星的半长轴,给出了星座纬度幅角和半长轴之间的关系,提出了星座构型的自主维持策略,但该方法仅给出了面内的关系,且未对星座运行中的误差进行分析。
与空间站长期共轨飞行的航天器轨道维持问题中,两航天器的轨道衰减率不同、主星轨控时机不定、共轨飞行轨道面还需满足后续交会对接的共面条件,这些因素给共轨策略的设计带来了较大挑战,本文基于共轨飞行的相对轨道参数演化关系,考虑J2摄动、大气阻力、轨道机动等因素,推导升交点赤经、倾角、相位、半长轴等相对参数间的解析关系,在此基础上针对空间站共轨飞行任务等工程应用背景设计了标称共轨轨道,制定了共轨飞行维持策略,进行了共轨飞行误差分析,包括定轨误差、控制误差、环境预报误差和面质比误差等带来的共轨飞行过程中升交点赤经偏差和相位偏差的解析表达式的推导,以及相应的数值分析算例,所得分析结果在空间站共轨飞行任务中有重要应用价值。
1 共轨飞行相对轨道参数的关系
环绕地球低轨飞行的航天器在轨飞行过程中轨道参数变化主要受到大气阻力、J2摄动、太阳引力摄动和轨道控制的影响。其中大气阻力会使轨道半长轴减小,但不改变轨道面,对轨道倾角和升交点赤经无直接影响。J2摄动为地球非球形摄动的主要项,对轨道面影响较大,对半长轴a、偏心率e和倾角i的影响是周期性的,不存在长期摄动项。太阳引力摄动主要影响轨道倾角,对于轨道高度相近的两低轨航天器,轨道倾角的相对变化量为小量[9]。
对于近圆轨道下共轨飞行的航天器,主要关注其相对于主航天器的半长轴、倾角、升交点赤经和相位等各参数之间的相互影响关系,其中倾角变化较小可单独考虑。本文主要分析相对轨道参数,即两航天器之间的半长轴差Δa、升交点赤经差ΔΩ和纬度幅角差Δθ(相位)之间的关系,在此基础上提出共轨飞行的轨道维持策略和误差分析方法。
1.1 升交点赤经差、半长轴差与相位的关系
1.1.1 升交点赤经差随时间的变化关系
考虑J2摄动的影响,升交点赤经的变化为
(1)
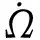
(2)
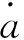
1.1.2 相位随时间的变化关系
为推导相位随时间的变化关系,考虑轨道角速度方程
(3)
式中:n为轨道平均角速度,对式(3)取变分再积分可得卫星在轨道上的角位置相对标称位置的相位偏差
(4)
1.1.3 相位与半长轴差的变化关系
(5)

图1以空间站共轨飞行任务为例,采用高精度轨道预报模型,仿真得到的不同初始半长轴差对应的相对相位演化关系,其中初始半长轴差分别为Δa=1km、Δa=2km、Δa=2.5km和Δa=3km,其最远相位分别为-33.4°、-75.9°、-110.6°和-155.6°,可见通过对共轨飞行航天器初始半长轴的偏置,可以将共轨飞行的相位维持在一定范围内。
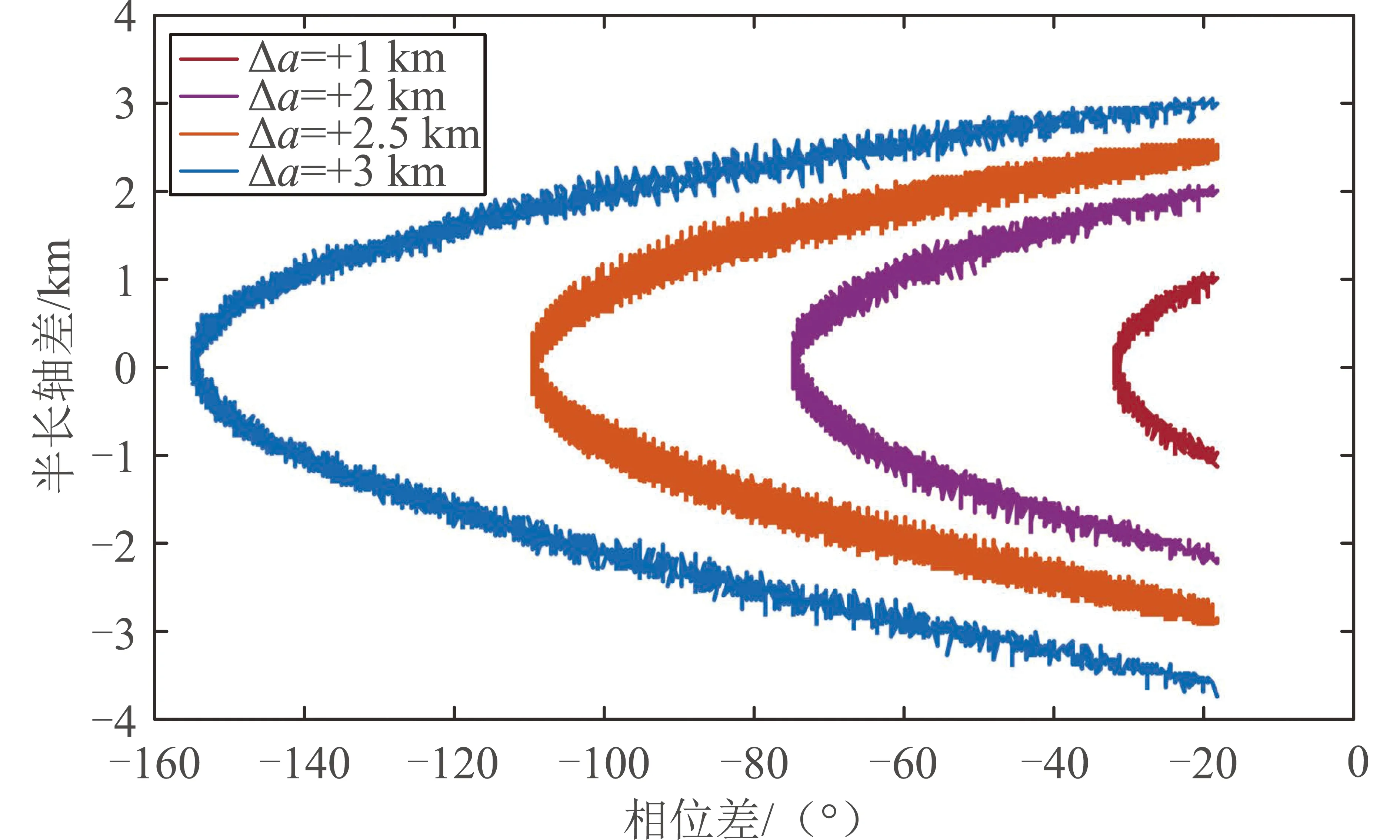
图1 不同初始半长轴差对应的相对相位演化Fig.1 Evolutions of relative phase corresponding to different initial semi-major axis
1.1.4 升交点赤经和相位之间的关系
根据式(2)和式(4),可得到升交点赤经差和相位差之间的关系
(6)
由式(6)可知,升交点赤经差与标称轨道半长轴的倒数的平方、倾角和相位差有关。考虑到两共轨飞行航天器的半长轴和倾角的偏差较小,因此在设计过程中可将系数k近似为常值。在共轨飞行任务中,通过半长轴偏置和定期轨道维持,可将两器相角差维持在一定范围内,则式(6)表明两器的升交点赤经差也会维持在一定范围内,即是被动稳定的。
表1给出了目标轨道高度在380~410km之间,倾角在40°~43°之间,不同组合下k值的计算结果。
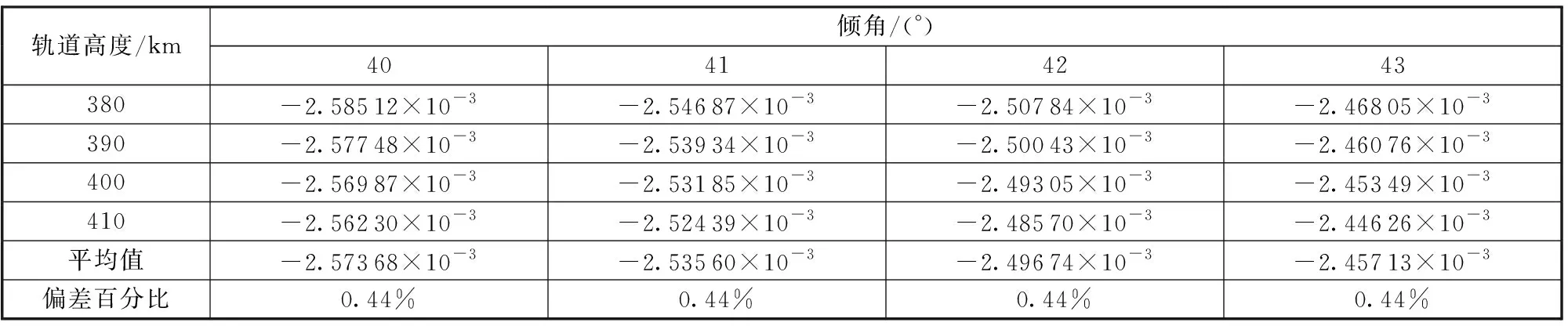
表1 不同倾角和高度下k值Table 1 Value of k in different initial inclination and altitude
从表1可知,相同倾角下,目标轨道高度380~410km内升交点赤经差与相位差的线性系数(斜率)k的偏差仅0.44%。
1.2 倾角对升交点赤经的影响
在仅考虑倾角变化的情况下,对式(1)取变分再积分可得
(7)
式中:Δi为倾角变化量,式(7)也给出了倾角误差对升交点赤经影响的解析表达式。可以看出,升交点赤经偏差与初始倾角偏差成正比。当倾角存在初始偏差,升交点赤经偏差随时间线性增加。
2 标称共轨飞行轨道和轨道维持策略
在与空间站长期共轨飞行的航天器轨道设计中,需要考虑两航天器的轨道衰减率不同、主星轨控时机不定和转交会对接轨道的共面约束等因素,本节以目标航天器(空间站)自由飞行且定期进行轨道维持的任务场景为例,说明前述分析结果在标称共轨飞行轨道设计中的应用,包括所得标称共轨飞行轨道特性和轨道维持策略的设计结果。数值计算中采用的轨道模型包括:①地球引力场模型采用JGM3的32×32阶次引力场模型;②太阳、月球三体引力;③采用NRLMSISE 2000大气模型,其中Kp=3,F10.7指数分别考虑F10.7=120、F10.7=110和F10.7=130;④目标航天器的面质比为0.0056m2/kg,共轨飞行航天器的面质比为0.0068m2/kg。轨道参数统一采用平根进行描述。
2.1 标称共轨飞行轨道
根据前面讨论的不同初始半长轴差对应的相位演化关系,可以通过在预定初始相位设置共轨飞行航天器与目标航天器的半长轴差,将标称共轨飞行轨道设计成类似图1所示的包含定期升轨维持的周期性飞行轨道。
不失一般性,标称情况下考虑空间环境的F10.7=120,目标航天器初始轨道高度为400km,倾角为40°。假定目标航天器的高度维持在380~400km,其控制规律为当高度降低到380km时进行轨道维持。首先通过仿真计算在空间环境F10.7=120情况下,目标航天器的控制周期为95.889天。然后设计共轨飞行航天器与目标航天器同步控制,其初始时刻在目标航天器后方20°相位处,一个目标航天器轨道维持周期内,共轨飞行航天器从后方20°相位逐渐远离目标航天器,然后再回到后方20°相位处。通过式(4)计算得到的初始半长轴为2.365km,数值仿真计算的初始半长轴为2.243km,偏差5.2%。
图2和图3分别为共轨飞行航天器在共轨飞行期间相对目标航天器的相位和升交点赤经随时间的变化关系,可以看出相位和升交点赤经的变化规律刚好相反,且解析法也较好地近似了两个参数的变化规律。图4为共轨飞行航天器相对目标航天器的半长轴和相位的关系,初始时刻共轨飞行航天器半长轴大于目标航天器,因此逐渐远离目标航天器,但由于其面质比较目标航天器大,当其半长轴衰减到与目标航天器半长轴一致后半长轴小于目标航天器,因此逐渐接近目标航天器,其间最远端相位为91.5°。
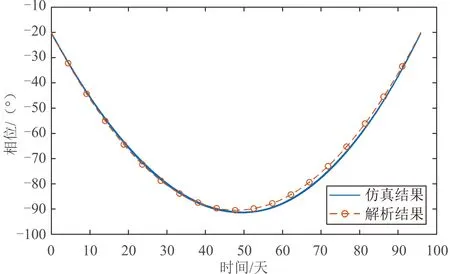
图2 共轨飞行相位随时间的变化曲线Fig.2 Curves of phase change with time during co-orbital flying
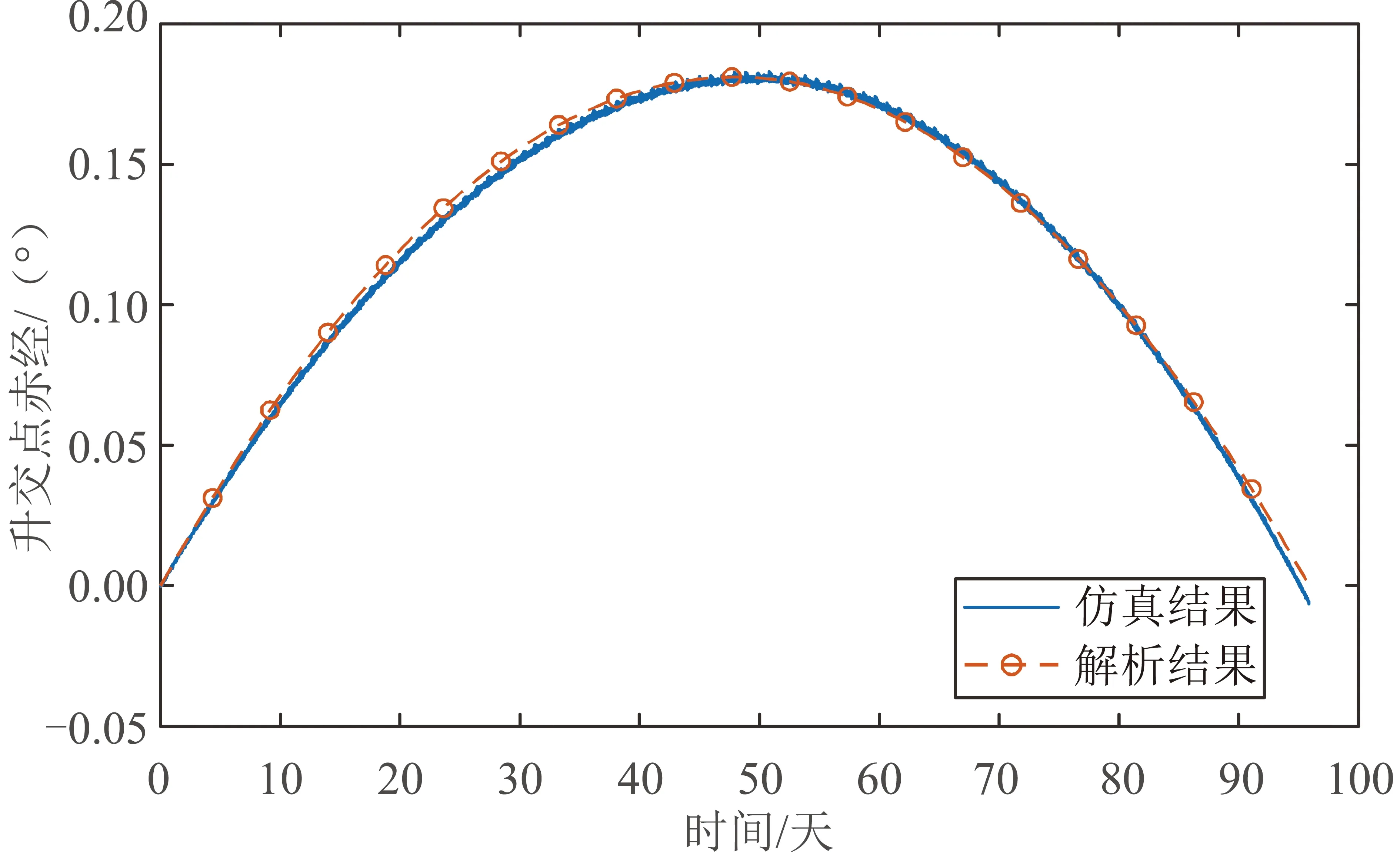
图3 共轨飞行升交点赤经随时间的变化曲线Fig.3 Curves of RAAN change with time during co-orbital flying
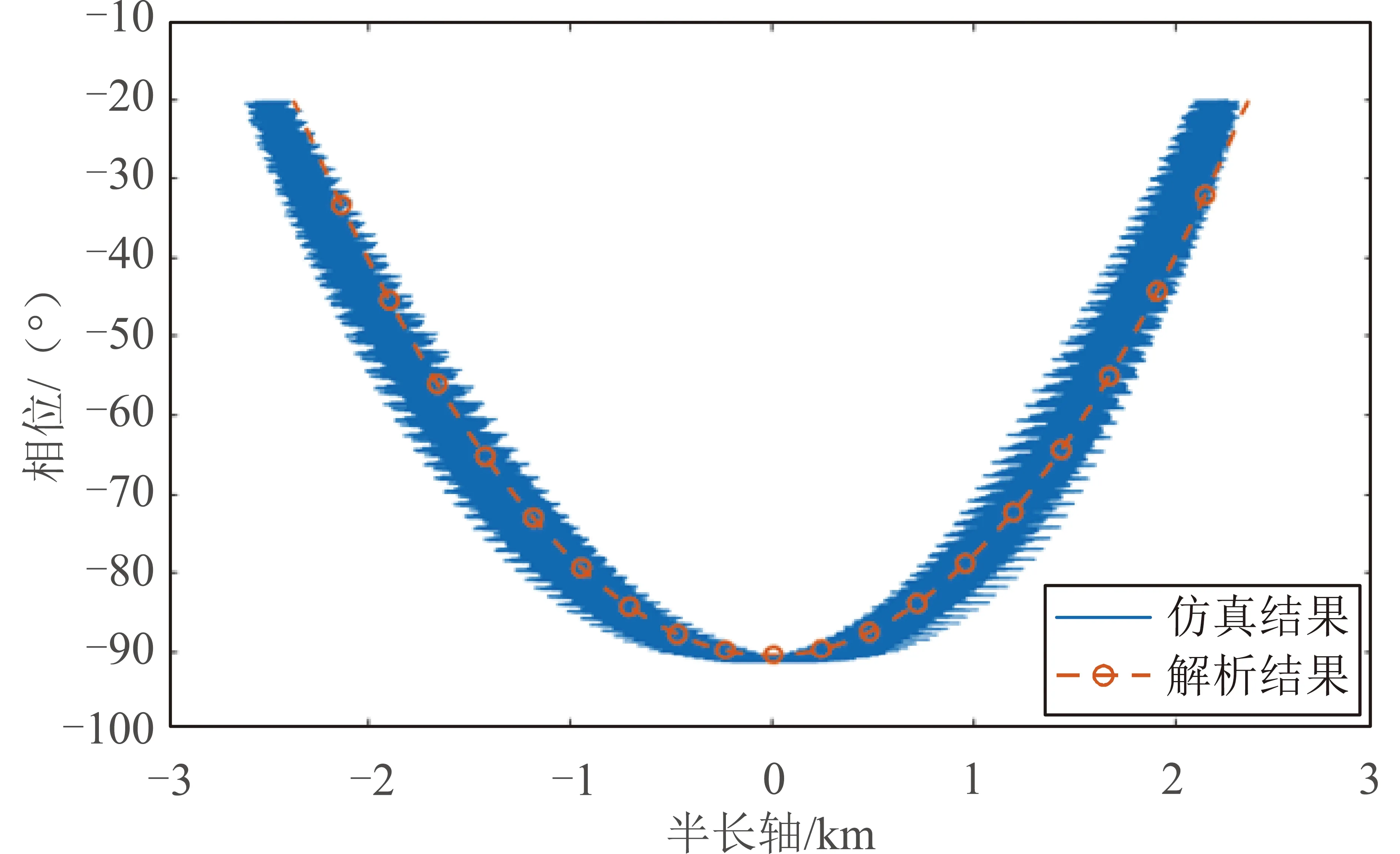
图4 共轨飞行半长轴-相位关系Fig.4 Relationship between semi-major axis and phase during co-orbital flying
图5为共轨飞行相位和升交点赤经之间的关系,按共轨飞行航天器远离和接近目标航天器的相对运动过程可分为两个阶段。其中Phase1为相位远离目标航天器阶段,采用最小二乘法拟合共轨飞行航天器和目标航天器的相位和升交点赤经的关系,得到系数kPhase1=-0.00253,其与表1的偏差为1.5%;Phase2阶段为相位接近目标航天器的阶段,拟合得到系数kPhase2=-0.00262,其与表1的偏差为1.8%。两者系数不一致的原因为:在Phase1阶段目标航天器高度变化范围在400~390km之间,在Phase2阶段目标航天器高度变化范围在390~380km之间。
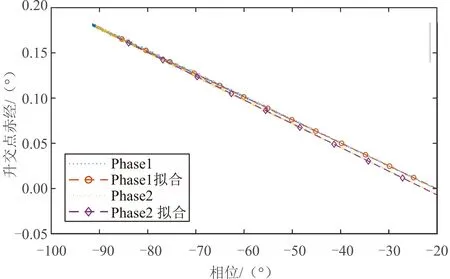
图5 共轨飞行相位-升交点赤经关系Fig.5 Relationship between RAAN and phase during co-orbital flying
2.2 共轨飞行维持策略
基于前述标称轨道设计以及相对轨道参数关系的分析结果,可制定如下共轨飞行航天器的轨道维持策略。
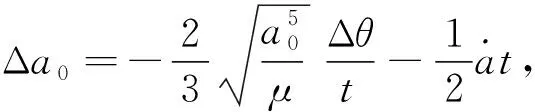
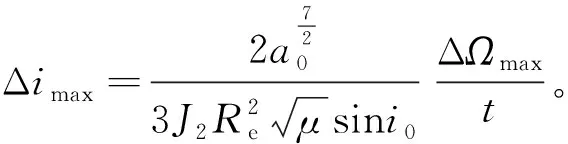
(3)面外升交点赤经控制:根据式(6),理想情况下升交点赤经相对相位被动稳定,但由于存在摄动和倾角初始偏差带来的误差累积,升交点赤经和相位偏离线性关系。共轨飞行过程中的轨道面还需满足后续转交会对接时两航天器共面——即相位为零时升交点赤经偏差为零,按照式(6)不同的相位对应不同的升交点赤经偏差量,因此共轨飞行过程中可根据当前两航天器的相位求得此时对应的理论升交点赤经差ΔΩt=k(a0,i0)θ0,再与实际测量的升交点赤经相比较得到升交点赤经修正量。如当两航天器在相位差为90°的位置,此时对应的标称升交点赤经差为ΔΩt=0.2295°(取k=0.00255),如果当前实际升交点赤经差为0.27°,则升交点赤经控制的修正量为0.0405°。
如图6所示为一典型的共轨飞行轨道,初始时刻航天器相对于空间站在A处,此时相位差为20°,高度差为2.365km;经过约48天后远离空间站到达最远相位C处,此时相位差为90°,高度差为零,升交点赤经按照式(6)的线性关系计算为0.2295°,如果实际飞行过程中升交点赤经差为0.27°,则对应的修正量为0.0405°;修正后再经过约48天后到达C处,此时相位差为20°,高度差为-2.365km;再经过半长轴控制和倾角控制回到A处,完成一次共轨飞行。
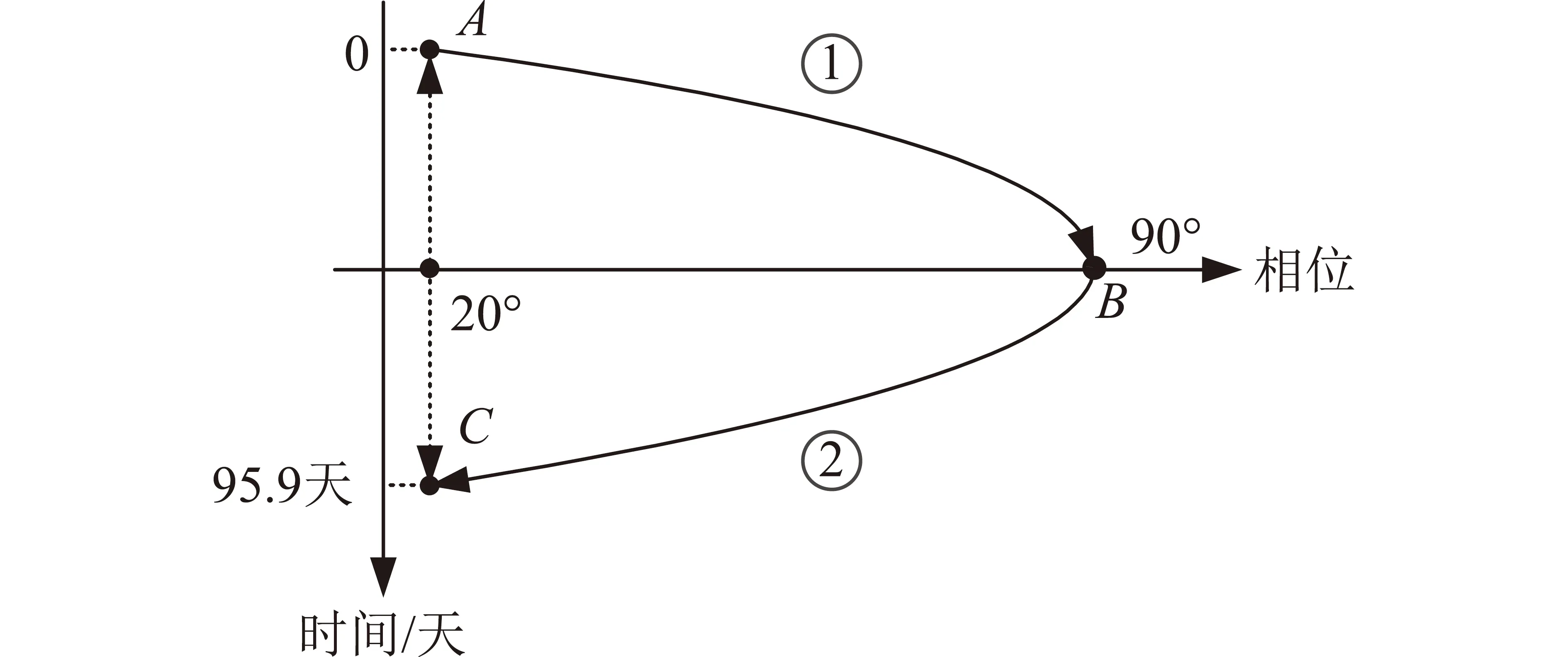
图6 共轨飞行过程Fig.6 Stage of co-orbital flying
3 共轨飞行误差分析
共轨飞行的误差主要包括由计算模型误差带来的半长轴计算误差、定轨误差、轨道控制误差、环境预报误差、面质比误差、倾角控制误差等,在这些误差作用下共轨飞行一定时间后会带来相位偏差。其中计算误差、定轨误差、轨道控制误差三项均可等效为初始半长轴偏差;面质比误差可等效为环境预报误差;倾角控制误差已在式(7)中进行了分析。
3.1 倾角偏差对升交点赤经的影响
在2.1节标称轨道的基础上,考虑在共轨飞行的初始时刻存在倾角偏差,仿真一个共轨周期后的升交点赤经累积偏差。取仿真开始时刻倾角相对标称值的偏差为δi=±0.001°,一个共轨周期95.889天内仿真计算和解析计算的升交点赤经变化如图7所示,表2为一个共轨飞行周期结束后的升交点赤经偏差,可见解析计算结果与仿真结果相比偏差小于3%。

表2 初始倾角偏差下一个共轨飞行周期结束后的升交点赤经偏差比较Table 2 Comparison of simulation and analytical results of RAAN in different initial inclination
上述分析表明,共轨飞行期间的倾角偏差会造成升交点赤经偏差随时间线性累积,例如当倾角偏差0.001°则一个共轨飞行周期(96天)后的升交点赤经偏差增加0.009°。因此,共轨飞行中需要设计倾角偏差控制阈值或定期进行倾角维持以减小共轨飞行期间的面外维持燃料消耗,也可通过对倾角的偏置实现对升交点赤经的控制。
3.2 半长轴偏差对共轨飞行相位的影响
对式(4)取变分后得共轨相位误差δθ与半长轴偏差δa的关系为:初始半长轴偏差带来的共轨飞行相位误差。
(8)
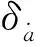
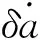

表3 不同初始半长轴偏差下终端相位偏差仿真结果和解析计算结果比较Table 3 Comparison of simulation and analytical results of phase in different initial semi-major axis
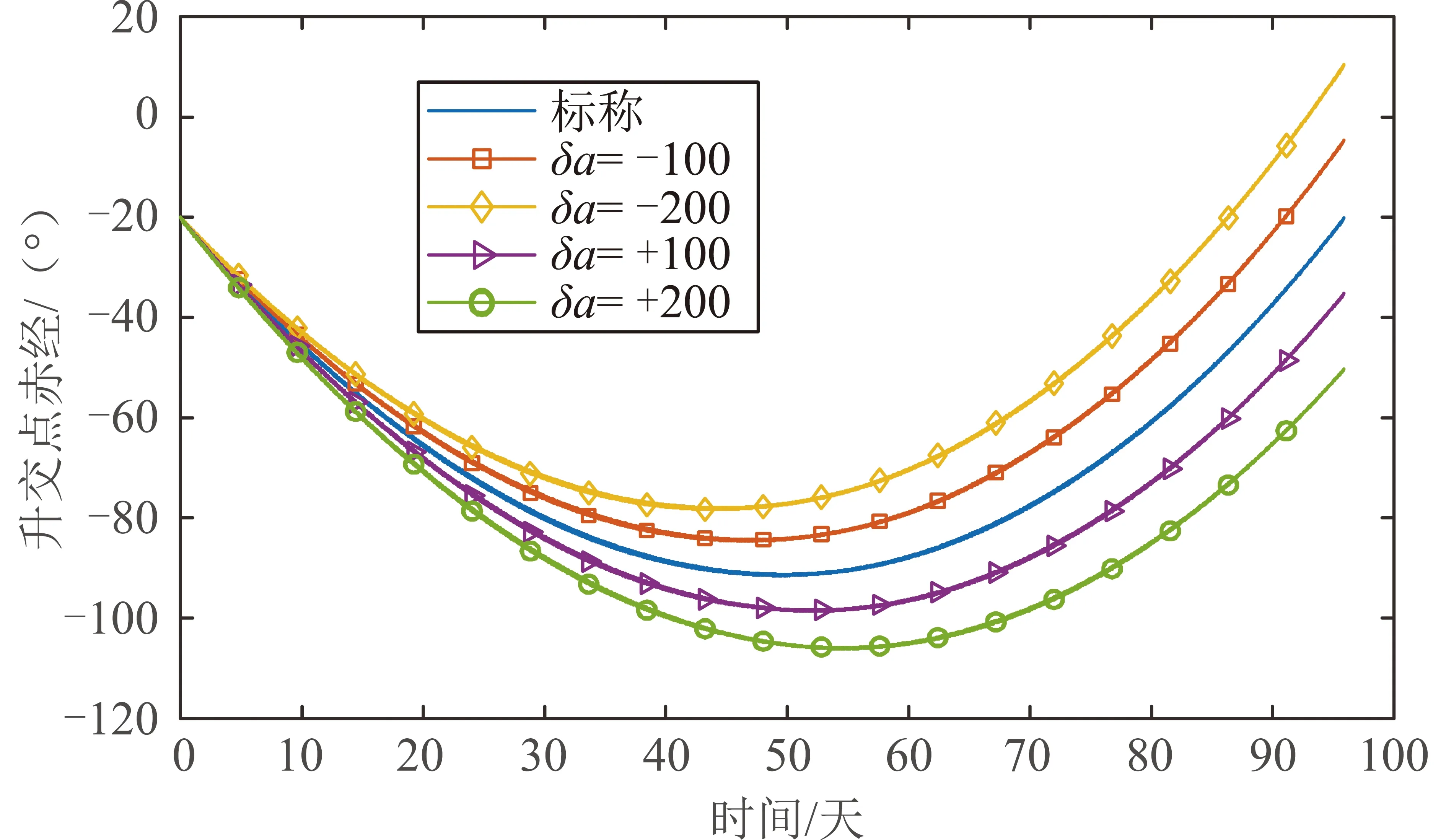
图8 不同初始半长轴偏差下相位随时间的变化Fig.8 Evolutions of phase corresponding to different initial semi-major axis
上述分析表明,在初始半长轴偏差影响下,共轨飞行相位误差与飞行时间近似呈线性关系,例如当初始半长轴偏差200m,则共轨飞行90天后的相位偏差约31°。因此,共轨飞行任务中需要尽量提高定轨预报精度和变轨控制精度。
3.3 环境偏差和面质比偏差对共轨飞行相位的影响
环境预报误差和面质比误差,最终的影响都是半长轴的衰减,因此都可通过式(4)对半长轴的衰减率的变分来计算。因此共轨飞行相位的误差δθ与环境误差或面质比误差的关系为
(9)
式中:pc为环境误差或面质比误差百分比。相位误差与其近似成线性关系和飞行时间成平方关系。
在2.1节标称大气参数F10.7=120的标称轨道基础上,考虑偏差情况下的大气参数分别为F10.7=110和F10.7=130两种情况,两者对应的大气密度相对F10.7=120的偏差分别为-15.4%和+16.7%,对应的目标航天器的控制周期分别为116.266天和80.096天。图9为仅考虑环境偏差下,不同空间环境对应的相位随时间的变化关系。尽管存在环境偏差,由于初始半长轴与F10.7=120条件下的半长轴一致,一个共轨飞行周期结束后仍然会回到初始相位,但共轨飞行过程中的最远端相位随空间环境的减小而增大。该结论也与2.2节共轨维持策略1和式(5)一致:当初始半长轴偏置不变的情况下即Δa(t=0)=+Δa0,空间环境变化影响共轨飞行周期,但在一个共轨飞行周期结束后共轨飞行航天器仍然会回到初始相位且有Δa(t=end)=-Δa0。表4给出了不同空间环境下的最远端相位仿真结果和解析计算结果,最远端相位由标称的-91.485°分别变为-105.115°(F10.7=110)和-81.135°(F10.7=130),且解析法的计算误差小于3.5%。
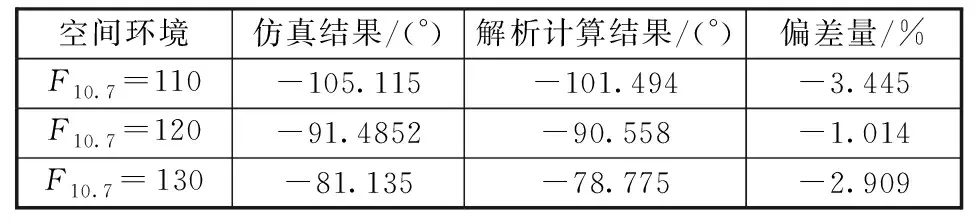
表4 不同空间环境下的最远端相位仿真结果和解析计算结果比较Table 4 Comparison of simulation and analytical results of maximum phase in different atmospheric
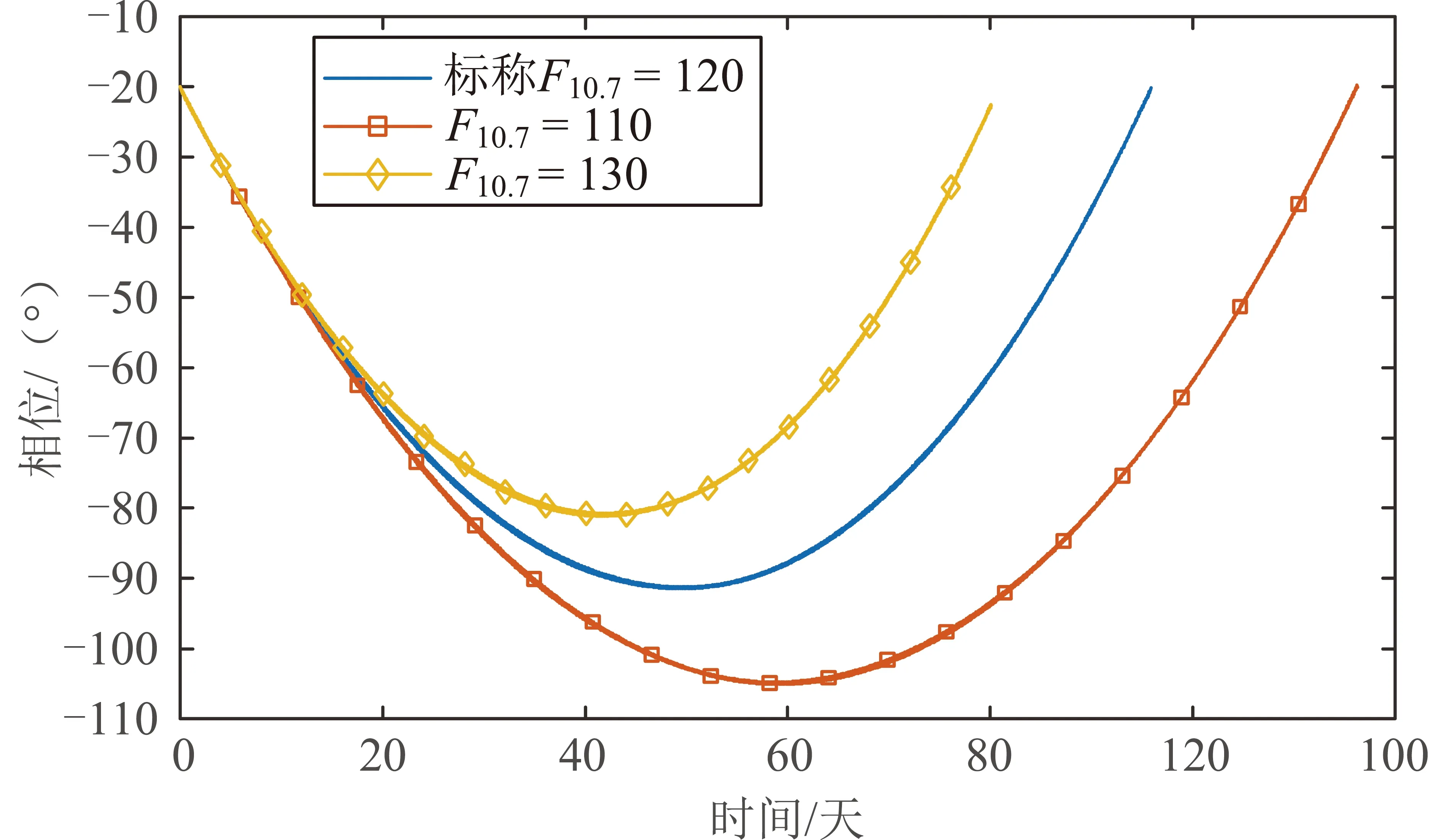
图9 不同空间环境下相同初始半长轴偏差对应的相位随时间的变化Fig.9 Evolutions of phase corresponding to different atmospheric
图10以标称轨道为基准,分别绘制了考虑空间环境变为F10.7=110、空间环境变为F10.7=130和空间环境变为F10.7=130且初始半长轴偏差+100m三种情况下60天内共轨飞行相位与标称情况下的偏差,可见随着时间的增加解析计算的精度降低,其中前两种情况的解析计算按照式(9)计算,第三种情况按照式(8)和(9),即环境偏差和半长轴偏差的线性叠加计算。表5给出了时间分别为50天和60天时的相位偏差数值仿真和解析计算结果,其中50天的解析计算结果误差小于7%,60天的解析计算结果误差小于15%。

表5 不同空间环境和初始半长轴偏差下相位偏差仿真结果和解析计算结果比较Table 5 Comparison of simulation and analytical results of phase deviation in different atmospheric and initial semi-major axis
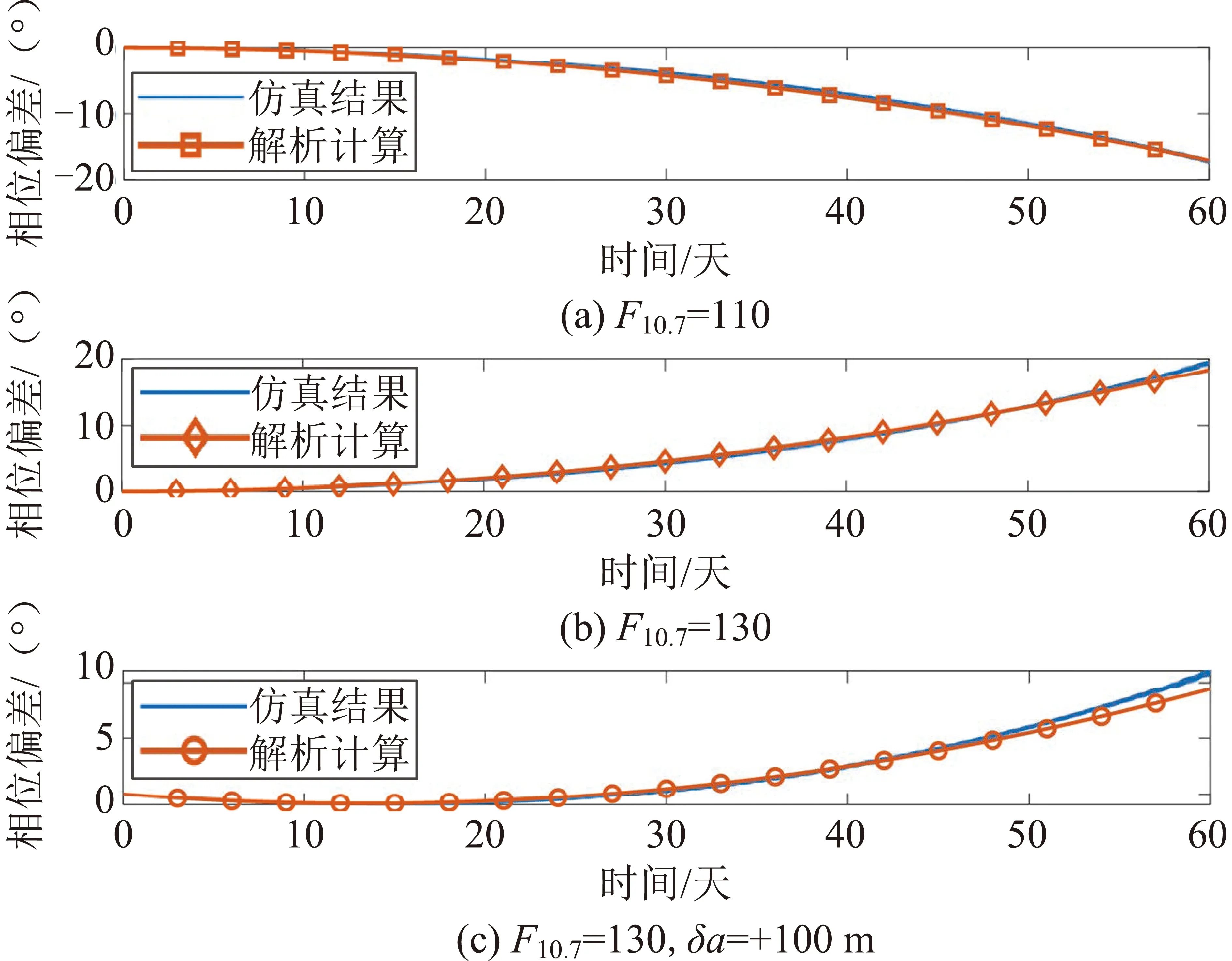
图10 不同空间环境和初始半长轴偏差对应的相位偏差随时间的变化Fig.10 Evolutions of phase corresponding to different atmospheric and initial semi-major axis
另一方面,在2.1节大气参数F10.7=120的标称轨道基础上,考虑共轨飞行航天器相对目标航天器的面质比增加56.7%,按照式(9)的计算方法解析计算相位偏差和仿真结果如图11所示,可见解析计算能很好地近似仿真结果。如当共轨飞行时间为60天时对应的解析计算相位差为62.542°,仿真得到的相位差为61.169°,解析计算偏差仅2.24%。
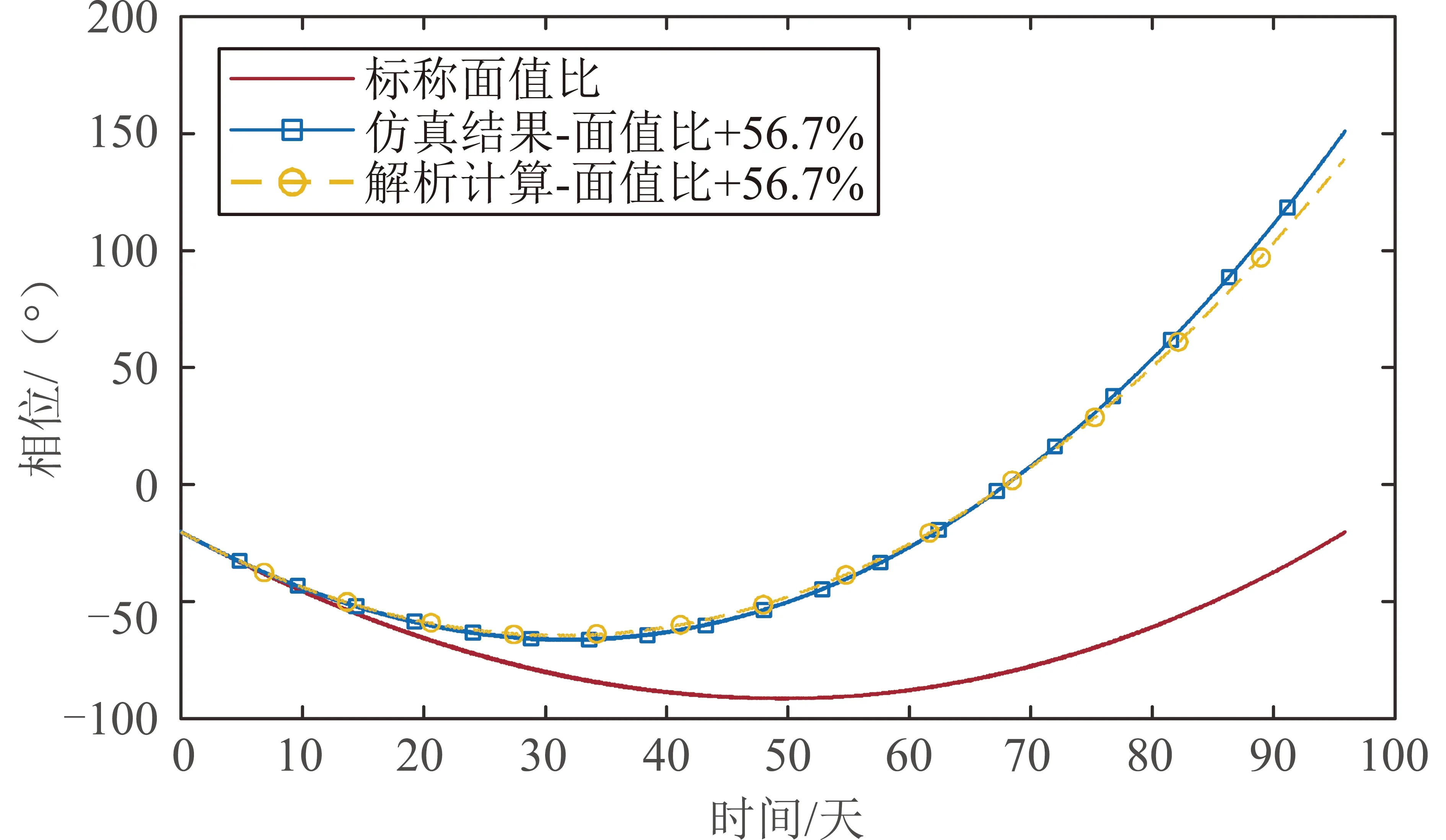
图11 面质比存在偏差下的相位偏差随时间的变化Fig.11 Evolutions of phase corresponding to different area-mass ratio
上述分析表明,在环境预报偏差或面质比误差影响下,共轨飞行相位误差与飞行时间呈平方关系,例如当环境偏差16.7%或面质比偏差56.7%,则共轨飞行60天后的相位偏差分别为19.6°和61.2°,因此需要定期更新大气模型或航天器的面质比模型。
4 结束语
本文针对与空间站长期共轨飞行的航天器轨道维持问题,在分析两航天器的半长轴、倾角、升交点赤经和相位等相对轨道参数演化规律的基础上,给出了相对空间站共轨飞行的标称轨道设计方法和相应的轨道维持策略,此外还进一步推导了考虑定轨误差、控制误差、环境预报误差和面质比误差等对共轨飞行轨道的影响。
分析结果表明,本文提出的解析误差分析计算方法能较好地近似数值仿真分析结果,对于共轨飞行任务,面内控制可通过共轨飞行航天器相对目标航天器的相位计算半长轴的维持量;面外升交点赤经的修正量可通过升交点赤经差与相位差的简化公式ΔΩt=k(a0,i0)θ0计算得到且偏差小于2%,倾角偏差控制阈值可以通过倾角偏差与升交点赤经偏差的线性关系得到。此外,初始半长轴偏差、环境预报偏差或面质比误差均会导致共轨飞行相位相对标称设计发生显著偏差,需要尽量提高定轨精度和变轨控制精度,特别是要定期更新大气模型或航天器的面质比模型。因此,本文基于解析计算方法设计的共轨维持策略和误差分析方法大大简化了共轨飞行策略的设计,在近地共轨飞行任务中有重要工程应用价值。

