热敏电阻在航天器应用的线性化研究

杨素君 张强 吴显林 曹剑峰 孙家林

(1 北京空间飞行器总体设计部 空间热控技术北京市重点实验室,北京 100094)(2 山东航天电子技术研究所,山东烟台 264670)

航天器上常用的测温元件有负温度系数(NTC)热敏电阻、铂电阻、热电偶。相对于热电偶,NTC热敏电阻不需要冰点补偿,且信号不易被干扰。相比铂电阻,NTC热敏电阻的阻值-温度系数大,反应灵敏,且电阻大,测量引线的电阻可以忽略,用二线制就可以获得满意的精度,因此NTC热敏电阻在航天器上具有非常广泛的应用,其电阻值高、灵敏度高、响应时间短、环境适用性强的特性,便于航天器上进行测量和信号传输[1-4]。一般航天器上约有几百只测温元件,大型航天器上能达到上千只测温元件,99%以上的温度传感器都是采用的NTC热敏电阻。

航天器在轨受辐射、极端温度等环境因素影响以及可靠性的要求,当前选用的处理芯片主频最快为100MHz,内存容量一般几MB,因航天器上热敏电阻数量多,存贮满足精度的标定数据和查询处理对航天器数据处理系统相对困难,不适于使用复杂的电路设计和软件算法。尤其是现场可编程门阵列(FPGA)处理器,数据处理资源比较少,运算量大时会造成严重的布线拥塞,阻碍FPGA的快速互联,最终会影响到功能实现。

航天器热敏电阻在温度求解计算过程中需要进行对数等复杂运算,存在计算复杂且占用内存较大的问题,因此对于在轨不参与控制的热敏电阻测点,一般是把测量到的热敏电阻阻值对应电压值下传到地面,在地面计算出温度。在轨参与实时控制时,则必须由航天器上数据处理系统进行温度的实时计算。如果能将热敏电阻的温度相关特性曲线拟合成一次线性方程,就可以大大降低航天器上数据处理系统的计算量,使得温度控制易于实现。对于计算能力稍强的系统,也可以拟合为多项式,以避免对数和其他复杂运算。

本文基于航天器上常用的半桥测量电路和温度计算公式,发现经测量电路转化后的热敏电阻分压与温度的曲线存在线性区间。进一步研究了电路中上拉电阻大小对热敏电阻线性化的影响,理论分析了使用温度范围中点处上拉电阻的最佳取值,并将其应用在某航天器上测温热敏电阻的一次线性拟合中。同时比较了同上拉电阻取值和同残差条件下一次线性拟合与三次多项式拟合的优缺点,给出了使用上的建议。

1 航天器热敏电阻测温电路和温度计算方法

航天器上热敏电阻的测量电路采用了结构简单、工作可靠的半桥电路实现热敏电阻阻值的测量,热敏电阻采用二线制连接,将测量电缆的质量限制到最小,适应了航天器对装器质量方面的严苛要求,电路示意图如图1所示。电路中采用上拉电阻R与热敏电阻串联,形成半桥电路,测量输出电压U即为热敏电阻分压。热敏电阻分压在航天器上采集并进行模拟-数字(AD)转换后,分层值通过天地链路传送到地面或在轨实时计算出温度值。两个精密电阻分压形成热敏电阻测量基准电压,将基准电压反馈给数据处理系统,对电源电压E进行修正,可以有效的提高热敏电阻测量精度。电压计算如式(1)所示,热敏电阻阻值计算式(2)所示。计算出RT后,再通过温度计算公式计算出温度。

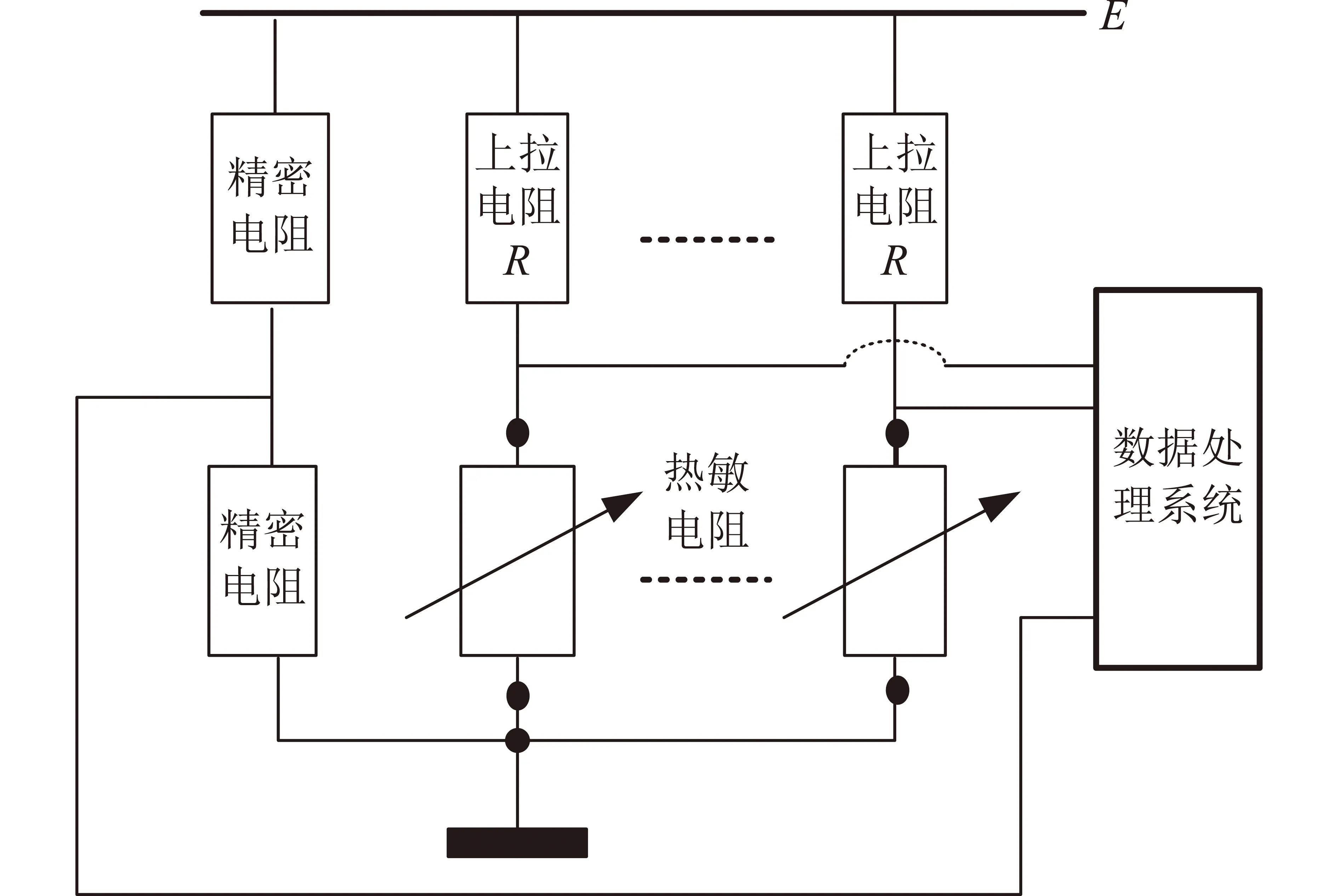
图1 航天器用热敏电阻测量电路示意图Fig.1 Measuring circuit of thermistor on spacecraft

(1)

(2)

式中:U为热敏电阻分压;R为上拉电阻;E为测量电路电源电压。

(3)

转化为温度t的计算为

(4)

式中:t为温度(℃);Rt为温度t时的热敏电阻阻值;a、b、c为热敏电阻拟合系数。

使用式(4)时温度计算精度大大增加,在航天工程中获得广泛应用。

采用半桥电路转换后,热敏电阻阻值与温度之间的关系转化为热敏电阻分压与温度之间的关系。热敏电阻阻值与温度曲线(Rt-t)、热敏电阻分压与热敏电阻阻值曲线(U-Rt)、以及最终的热敏电阻分压与温度曲线(U-t)分别如图2、图3、图4所示。可以看出,虽然Rt-t曲线和U-Rt也是非线性的,但是U-t曲线最终呈现为S型,整条曲线存在拐点,在拐点附近温度区间内存在线性。

图2 热敏电阻Rt-t特性曲线Fig.2 Rt-t curve of thermistor

图3 半桥电路转换后U-Rt曲线Fig.3 U-Rtcurve after half-bridge circuit conversion

图4 半桥电路转换后U-t曲线Fig.4 U-t curve after half-bridge circuit conversion

2 上拉电阻的影响研究及实际应用

2.1 上拉电阻对电压-温度线性化区间的影响研究

在半桥电路中,电源电压一般随系统设计确定,唯一需要确定的就是上拉电阻R的取值。以航天器上使用较多的MF501互换型热敏电阻为例,图5给出了上拉电阻不同阻值时输出电压U与温度t之间的关系曲线。如上分析,U-t曲线呈S型,在其拐点(即斜率变化率为零的位置)附近存在U-t线性化较好的区域。拟合误差不大于1℃条件下,7种上拉电阻取值下的线性区间如表1所示。从表1数据可以看出,上拉电阻越小,残差不大于1℃下的线性区间越宽,线性区越向高温区移动。此外,改变上拉电阻R的取值,可以改变半桥电路线性温区的中心位置和线性区宽度。

表1 不同上拉电阻下线性区间范围Table 1 Linear range under different pull-up resistors

图5 不同上拉电阻值的U-t曲线Fig.5 U-t curve under different values of pull-up resistance

探索上拉电阻R取值对线性区间中心温度值的影响:依据式(1)和式(3),对式(1)求导,一阶导数表示电压-温度曲线的斜率,二阶导数表示电压-温度曲线斜率的变化率,使得二阶导数为0的点即是电压-温度曲线斜率不变的点,即U-t曲线的拐点,也是线性化区间的中心点。

令U对t的二阶导数为0,整理得

(5)

式中:TM为热敏电阻分压-温度曲线拐点处的温度值;RtM为TM所对应的热敏电阻阻值。

如果热敏电阻用于在小区间温度测量,可以调整R值的大小,使得工作温度区间中点在拐点附近,在此附近区间热敏电阻输出线性化,实际使用的温度区间落在U-t曲线的线性温度区间内。这样,使用温度区间内线性化好,在此温度范围内按照一次线性拟合,可以达到简化运算的目的。表2给出了MF501型热敏电阻在温度区间中点温度为25℃、15℃、5℃时的最佳上拉电阻值和线性化区间(拟合误差不大于0.6℃)。可以看出在温度区间中点温度为5℃时,上拉电阻约为10kΩ,线性区间为

表2 不同上拉电阻下线性区间范围Table 2 Linear range under different pull-up resistors

-13～+24℃,基本覆盖航天器常用控温值,可用线性公式计算温度,且精度上满足航天器常用测温精度0.6℃的要求。

在这里需要注意的是,如果R取值太小,将会导致流过热敏电阻的电流过大,致使热敏电阻自热效应产生的测量误差较大。R的取值应在线性化和自热效应误差两方面权衡取值,应保证热敏电阻的电流至少不大于5mA,有条件的情况下尽可能减小热敏电阻的电流。

2.2 线性化拟合在航天器中的实际应用

在某航天器实际运用中,所控目标温度在0～20℃范围内,使用互换型MF501热敏电阻(测量范围为-40～+70℃),软件系统为FPGA,控制逻辑中需要在轨计算出当前温度,驱动控制机构,逐步逼近控温目标值。

为适应FPGA系统,先简化温度计算公式,应用温度-电压曲线拐点附近线性化的特点和式(5),对其进行一次线性拟合。选取0～20℃的中点10℃作为拐点处温度,根据前文的分析,可在10℃两侧温区内获得线性区间,简化为一次线性计算。将MF501热敏电阻系数(a=-6.01188;b=4622.53337;c=-86421.72414)、10℃时的阻值10255.6Ω带入式(5),计算出此时最优的上拉电阻R为7889Ω。(为方便选取元器件,上拉电阻值取8kΩ。)

实际使用中均是测量热敏电阻分压U,通过计算得出温度值t。对0～20℃区间内的温度-热敏电阻分压关系的拟合曲线见图6,可看出其线性拟合度好,决定系数(Adj.R-Square)达到了0.99997,残差在-0.09～+0.07℃范围内。

图6 0～20℃线性拟合Fig.6 Linear fitting at trange of 0～20℃

3 其他拟合方法分析和比较

3.1 全温度范围内线性拟合和多项式拟合比较

对MF501型热敏电阻-40～+70℃全温度范围内,取上拉电阻为8kΩ时,分别进行线性拟合和三次多项式拟合。线性拟合曲线如图7所示,残差小于1℃时的线性区间为-12.8～+33.6℃,温度跨度46.4℃。多项式拟合曲线如图8所示,残差小于1℃时的温度区间为-36～+68℃,温度跨度为104℃,基本涵盖了全部测量范围。

图7 -40～+70℃线性拟合Fig.7 Linear fitting at range of -40～+70℃

图8 U-t曲线多项式拟合Fig.8 Cubic polynomial fitting of U-t curve

相对于一次线性拟合,三次多项式拟合适用于温度测量范围更宽的使用情境,在同样残差不大于1℃时,温度跨度为线性拟合区间的2倍。因此对于计算能力强的数据处理系统,为避免式(4)中的对数和开方运算,可以采用多项式拟合的方式进行温度计算。

3.2 占用内存和速度比较

为比较不同计算公式占用资源情况和运算速度,在仿真平台上对一次线性公式、三次多项式和航天器常用的公式(式(4))均进行了1000万次计算测试,对占用内存和计算用时进行了比较,结果如表3所示。

表3 占用资源和计算时间比较Table 3 Comparison of resource occupancy and computation time

从表3中可知,3个公式中,一次线性公式占用内存最少,是式(4)的1/3,而计算用时约是式(4)的1/31。三次多项式公式占用内存与航天常用公式相当,但计算用时约是式(4)的1/6。

4 结论

本文研究了热敏电阻半桥测量电路中上拉电阻对NTC热敏电阻线性补偿效果的影响,并进行了对比研究分析,得出以下结论:

(1)使用半桥电路测量热敏电阻,最终得到的热敏电阻分压与温度曲线存在拐点,在拐点附近有较好的线性。

(2)同样残差下,上拉电阻越小,热敏电阻分压与温度曲线的线性区间越宽,线性区越向高温区移动,并理论推导出了最优上拉电阻计算公式。

(3)将一次线性拟合应用在某航天器0～20℃范围测量中,一次线性拟合后的残差小于0.1℃。一次线性公式计算速度快,占用内存少,因航天器上控温区间一般较窄,可推广应用在航天器控温温度的计算中,简化计算。

(4)使用三次多项式拟合时,残差小于1℃的温度跨度大大增加,是同样残差条件下的一次线性拟合区间的2倍,基本涵盖了全部测量范围。且三次多项式计算用时短,是目前常用公式的1/6,使用拟合的三次多项式更有利于提高计算效率。