大型梁式反力系统的结构力学特性研究

黄 锋,张 班,刘星辰,杨正旭,屈苗迪

(1. 重庆交通大学 山区桥梁与隧道工程国家重点实验室,重庆 400074; 2. 重庆交通大学 土木工程学院,重庆 400074; 3. 河南省交通规划设计研究院股份有限公司,河南 郑州 451450)

0 引 言

在实验室中,部分模型试验需要大吨位的加载系统,如高地应力隧道缩尺模型试验、足尺模型试验,这类大吨位的加载问题是实验室的重难点之一。加载系统一般由反力架、反力墙、反力梁等组成,并安装加载装置,实现对荷载的精确控制。

为了满足自身试验的加载要求,学者们对反力系统进行了设计和研究。涂熙等[1]设计了1 296 t吨位的反力体系,通过有限元和试验分析,验证了刚度满足试验要求;晁晓艳等[2]自行设计了反力架,但加载吨位较小;柴振岭[3]采用有限元数值模拟与理论分析相结合的方法,研制了一种适用于教学与科研的拉压双作用梁式反力架,但无法实现大吨位荷载试验;王辉等[4]通过试验和有限元分析了大吨位反力梁的应力和变形,提出设计时应对螺栓孔附近进行加固,但并未研究极限荷载下的反力梁力学特性。

大吨位工况下,由于反力梁及连接节点结构刚度不足,在加载过程中会导致反力梁与试验对象产生整体相对位移及较大的挠度变形[5]。为实现加载装置对荷载的精致控制,需对反力系统进行结构强度分析。

目前,对结构强度的研究主要包括试验研究和有限元分析。周智海等[6]采用有限元分析,对高架桥影响轨道线路区间的最不利断面,进行了轨道结构位移与变形等相关安全影响的计算分析,研究了拟建市政道路高架桥对既有轨道结构的安全影响;杨敬东等[7]对绞车作业中4种工况的结构进行有限元强度校核,验证了绞车支撑结构加强方案合理可行。试验研究能直观准确获取结构的力学特性[8-9],但有些试验设计和实施条件要求高、控制严、难度大,在实际工作中有时难以做到。有限元分析应用广泛,但在本构模型选取、材料参数确定等方面存在较大困难,导致研究成果在指导实际工程时具有一定局限性[10]。将试验和有限元结合,在两者结果吻合较好的基础之上,再分析结构的受力特性[11]。

针对重庆交通大学隧道实验室地下结构三维加载试验平台的设计思路和结构特点,通过静载试验和有限元分析,对反力梁和螺栓进行强度验证和变形研究。同时,深入探索了极限荷载下的反力梁和螺栓的力学特性,为后续梁式反力系统的建设者提供良好的经验。

1 反力系统设计

重庆交通大学隧道实验室地下结构三维加载试验平台,其加载能力16 500 kN(1 684 t),底部采用高强度钢筋混凝土,侧面为高强度钢筋混凝土反力墙,顶部为大型钢结构反力梁,如图1。

图1 反力系统Fig. 1 Reaction system

1.1 设计思路

在反力墙的台座上,设有图2(a)所示的地脚螺栓孔,通过螺栓将反力梁与反力墙固定,组成反力系统,反力梁尺寸如图2(b)。

图2 设计图(单位:mm)Fig. 2 Design drawing

1.2 设计原则

1)底部采用的高强度钢筋混凝土、侧面的反力墙、顶部的大型钢结构反力梁以及螺栓连接节点处的刚度足够大,满足最大荷载量(1 684 t)的要求,同时要满足12%的安全储备。

2)反力系统自身的变形量,尤其是反力梁的变形量,要符合试验要求(反力梁长度的1/1 000)。

3)反力梁的结构简单,重量轻,方便吊装。

1.3 结构与特点

考虑结构组合效应,确定反力梁的结构形式,反力梁与反力墙通过螺栓连接,如图1。反力梁总长为12 900 mm,主体采用Q345B级钢板焊接而成,重44.75 t,连接螺栓采用40Cr钢,螺栓杆直径70 mm。平台最大加载1 684 t,可突破高地应力隧道缩尺模型试验的加载瓶颈,满足试验加载要求。

2 反力系统力学特性分析

反力系统的底部和侧面反力墙采用高强度钢筋混凝土浇筑而成,刚度足够大,满足最大荷载(1 684 t)下的变形要求,所以主要研究反力系统中钢结构反力梁和螺栓连接节点的力学特性。

2.1 有限元分析

采用有限元软件ABAQUS对反力系统进行分析,通过缘、腹板、隔板、支座端板、加劲肋板装配组成反力梁,不考虑焊接差异[12],材料使用Q345钢进行模拟。螺栓、螺母、刚性支座采用高强度钢材料,有限元模型中,钢材采用理想弹塑性模型,材料的力学性能见表1。

表1 钢材的力学性能Table 1 Mechanical properties of steel

图3(a)中底座的边界条件采用全约束,螺栓、螺母、支座和反力梁之间的接触面采用硬接触[13],根据GB 50017—2017《钢结构设计规范》,摩擦系数设置为0.15。考虑模型自重,采用3点加载,单点加载力为5 500 kN,加载位置如图3(b),加载区域由圆柱体和长方体组成,荷载加在圆柱体上,同时约束长方体x、z方形的位移,确保内部圆柱体在加载过程中沿y方向移动。模型结点总数225 852个,单元采用C3D8(8结点线性6面体),总数148 707个。

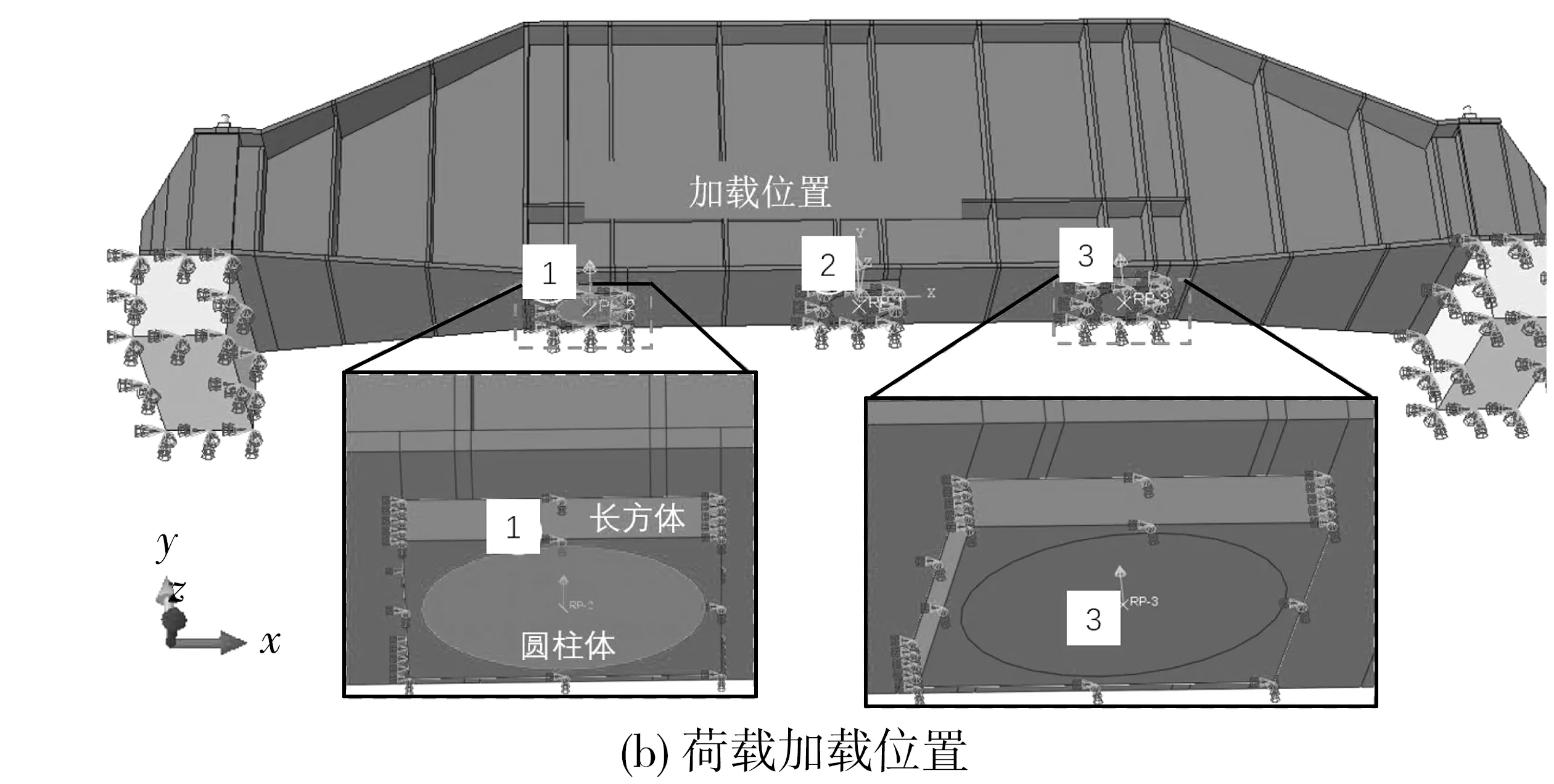
图3 有限元模型Fig. 3 Finite element model

反力系统构件的应力云如图4。图4表明:反力梁在螺栓孔区域发生应力集中,最大应力345 MPa,反力梁强度满足试验要求;螺栓最大应力551 MPa,螺栓强度满足试验要求。

图4 反力系统构件的应力云图Fig. 4 Stress nephogram of reaction system components

通过有限元分析,反力梁的竖向位移变形(放大100倍)如图5。反力梁上翼缘板的位移整体小于下翼缘板,表明上、下翼缘板之间的钢板存在压缩现象,下翼缘板的位移更能代表试验真实位移。

图5 反力系统y方向的位移云图(单位:mm)Fig. 5 Displacement nephogram of reaction system in the y direction

将螺栓支座沿x方向(反力梁轴线方向)的位移变形放大500倍,如图6。螺栓在螺母连接处,向反力梁方向发生内凹,最大位移0.550 mm。在内排螺栓顶部,发生远离反力梁方向的位移,最大变形值1.138 mm。

图6 x方向螺栓位移变形云图Fig. 6 Nephogram of bolt displacement and deformation in x direction

变形后的螺栓简图如图7,根据三角形公式,计算出螺栓变形角度α=0.3°,β=0.069°,表明螺栓节点属于半刚性结构。

图7 x方向螺栓位移变形简图(单位:mm)Fig. 7 Displacement and deformation diagram of bolt in X direction

选取一个内排螺栓,绘制其荷载-转角曲线,如图8。螺栓转角随荷载增加几乎呈直线增加,通过计算荷载和转角曲线的斜率发现,斜率随荷载的增加由3.17×10-5增加到3.74×10-5,增加了18%。

图8 荷载-转角曲线Fig. 8 Load-rotation angle curve

2.2 试验分析

反力系统单点最大设计荷载5 500 kN,顶部设置3个荷载加载点,3点同时加载,共计16 500 kN,集中荷载的作用点如图9。

图9 测点分布(单位:mm)Fig. 9 Distribution of measuring points

试验主要监测梁的竖向位移和应变。位移计布置在上翼缘板的两端、跨中和加载点的正上方,记为①～⑤,位置如图9。测点1～7用于监测梁上翼缘的应变,测点8～15用于监测梁下翼缘的应变,测点16～21用于监测梁中前钢板的应变,位置如图9。

为了测量最大设计荷载作用下反力梁的位移和应变等力学特性,试验先预加载、正常荷载加载,最后采用分级加载方案:以500 kN为步长,从0开始,共11步,3点同时加载,直到5 500 kN,停止加载。

通过试验测点应变数据,利用公式(1),获得试验测点应力,得到的荷载-应力曲线如图10。

图10 荷载-应力曲线Fig. 10 Load-stress curve

(1)

式中:εx为x方向的应变;σx为x方向的应力;E为弹性模量。

由图10可知:在加载过程中,上翼缘板测点的应力为正值,表明上翼缘板处于受拉区;下翼缘板测点8、15应力为正值,表明其位于受拉区,测点10、11、12应力为负值,表明其处于受压区,测点13测试中损坏,无读数,测点9、14的应力值在3 000～3 500 kN荷载区间,由正值突变为负值,表明其位置由受拉区变为受压区,原因可能是螺栓节点处的螺栓发生了滑移。荷载在2 500～3 000 kN区间,上翼缘板测点3、4、5的应力值出现了不同程度的降低,之后应力又继续上升;荷载在4 000～5 000 kN区间,上翼缘板测点3、4的应力出现了先减小后增大的现象;荷载在3 000～4 000 kN区间,下翼缘板测点8、15的应力再次出现了先减小后增大的现象。表明螺栓节点处螺栓可能发生了滑移,导致应力突然减小,出现了应力释放的现象,螺栓稳定后,测点应力继续增大。

加载引起的荷载-位移曲线如图11。①和⑤处测得的最大位移为1.69 mm和1.17 mm,表明螺栓连接的刚度不足,反力梁出现向上的整体位移。③位于梁中点,加载过程中,竖向位移最大,最大位移变形量10.91 mm。根据①和⑤处的位移,测得梁中点的实际挠度为9.48 mm,小于梁的要求变形量12.90 mm(梁长度的1/1 000)。

图11 荷载-位移曲线Fig. 11 Load-displacement curve

2.3 结果对比分析

为了验证有限元结果的准确性,将试验结果和有限元结果进行对比分析。

选取上翼缘板的测点1～4,进行应力对比分析。试验测点应力围绕有限元测点应力上下浮动,如图12,表明了有限元模型的准确性,图中FE、T分别为该点的有限元结果、试验结果。

图12 荷载-应力曲线Fig. 12 Load-stress curve

3 失稳下的力学特性分析

为研究反力梁在失稳下的力学特性,首先通过试验数据验证了有限元分析的准确性,然后采用有限元模型模拟失稳下反力梁的破坏变形规律。采用远大于极限荷载的力对反力系统进行加载,获取反力梁失稳的位移变形如图13(放大15倍)。

图13 反力梁位移变形Fig. 13 Displacement deformation of reaction beam

竖向肋板在底部产生了较大的水平变形,最大位移20.40 mm;水平肋板在中部产生了较大的竖向变形,最大位移64.97 mm;腹板在两端和底部产生了较大的z方向(垂直于腹板方向)变形,最大位移18.1 mm,具体位置如图13。

将螺栓极限荷载下的位移变形放大15倍,如图14。水平方向最大位移变形12.22 mm,竖向最大位移变形4.64 mm,z方向最大位移变形9.97 mm,具体位置如图14。

图14 螺栓位移变形Fig. 14 Displacement deformation of bolt

由图14可知:反力系统在设计中,需要加强反力梁竖向肋板底部、水平肋板中部、腹板的两端和底部处的刚度,以及螺栓水平方向的刚度,以提高反力系统的安全性和有效性。

4 结 论

通过对反力梁和螺栓节点的力学特性分析,发现螺栓节点底部的应力较大,在设计反力系统时,应加强对螺栓节点底部的反力梁刚度。同时,得到了如下结论:

1)通过试验位移数据和有限元分析,验证了反力梁的挠度变形满足试验要求。

2)根据加载后螺栓角度的变形分析,表明螺栓节点属于半刚性结构,同时螺栓转角随荷载增大呈直线增加趋势。

3)试验测点应力存在先减少后增大的现象,可能是螺栓节点处螺栓发生了滑移。

4)在超过极限荷载时,反力梁的竖向肋板底部、水平肋板中部、腹板的两端和底部,以及螺栓水平方向均发生了较大的位移变形,需增加这部分梁的截面惯性矩和螺栓水平方向的刚度,以确保反力系统的安全性和有效性。