检查井及井周路面影响下的车辆荷载动态特性

赵全满,王鑫均,卢晓锦,刘继法,胡文军

(1. 山东建筑大学 交通工程学院,山东 济南 250101; 2. 山东省道路工程绿色建造与性能提升工程实验室,山东 济南 250101; 3. 山东省泰安市公路规划设计院,山东 泰安 271001)

0 引 言

检查井是城市道路管网的重要组成部分,在城市管网系统建设和维护中具有重要作用。检查井与路面在结构和刚度方面具有较大差异,它的存在不仅破坏了道路结构完整性,而且在车辆荷载反复作用下极易产生各类病害。城市道路检查井及井周路面(指检查井周围一定范围内路面)养护后,在短期内极易再次发生破坏[1]。目前学者们对于检查井及井周路面的研究多集中在检查井及井周路面病害检测[2]、检查井沉降机理分析[3]、新型检查井结构[4]、井周路面病害机理和养护时机分析[5-6]及井周路面修补材料研发[7-8]等方面。

车辆经过井周路面时会产生一定的车辆冲击荷载[9],当车辆经过井盖时,井盖变形和振动较为明显,这时车辆振动和井盖振动会形成“叠加效应”,明显增大了车辆冲击荷载,并加速井周路面平整度劣化,反过来会导致车辆冲击荷载进一步增大,形成恶性循环。由此可见,车辆经过检查井及井周路面时,在井周路面平整度变化和井盖变形及振动作用下,车辆荷载特性复杂、冲击效应显著,这也是井周路面频频破坏的主要原因之一。

目前,对车辆荷载动态特性的研究主要有数学建模、数值分析和现场测试这3种方法。数学建模分析时,需要对所构建的车辆振动模型进行荷载动态特性分析,常用的车辆模型包括1/4车辆振动模型[10]、1/2车辆振动模型[11-13]和整车振动模型[14];数值分析时,需要借助各类数值分析软件,陈正伟等[15]利用TruckSim软件对沥青路面车辆荷载动态特性进行了分析,并提出了确定沥青路面养护时机的理论方法;现场测试方面,刘大维等[16]通过在车轴位置布设加速度传感器测试了车辆动载的随机特性,研究了随机动载与行驶速度的关系。总之,目前在常规路面的车辆荷载动态特性的研究方法成熟、成果颇丰,但鲜有学者对车辆在经过检查井及井周路面的车辆动态荷载特性展开研究。

车辆在经过检查井及井周路面时,其振动特性与常规路面存在明显不同。当车辆经过常规路面时,路面振动和变形对车辆振动特性影响较小,路面与车辆为弱耦合系统[17];当车辆经过检查井时,井盖振动和变形对车辆振动特性影响较大,井盖与车辆为强耦合系统[18]。故当车辆经过检查井及井周路面时,笔者将井盖振动和变形纳入车辆振动模型,建立了车-井盖耦合振动模型,并对车辆经过检查井及井周路面时的车辆荷载动态特性进行了研究,同时分析检查井沉陷量、行车速度、井盖刚度系数、井周路面病害导致的高差、井周路面坡度变化率这5大因素对车辆荷载动态特性的影响,为井周路面破坏机理及养护维修提供了理论依据。

1 检查井及井周路面病害调查

检查井结构一般由井盖、井筒、井圈、井室等部分组成,其结构如图1。笔者对城市道路检查井及井周路面病害及平整度展开了调查,发现井周路面平整度远低于一般常规路面[19]。为进一步厘清车辆在经过检查井及井周路面时的荷载动态特性,需要明确检查井及井周路面病害类型,确定井周路面破坏失效范围(病害范围)。故在检查井及井周路面病害调查时,笔者重点调查了井周路面病害类型和范围,为车辆荷载动态特性分析提供数据支撑。

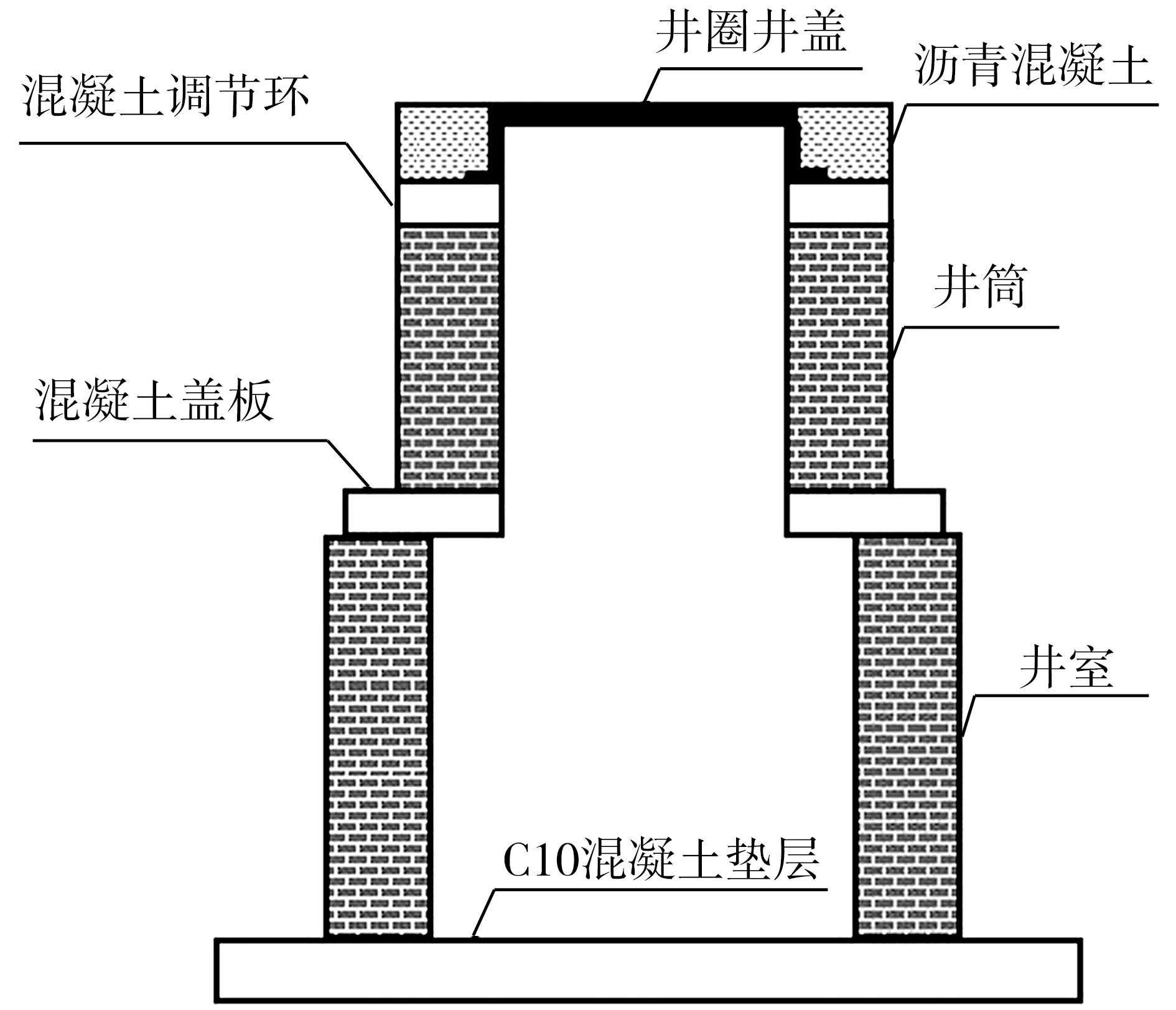
图1 检查井结构示意Fig. 1 Schematic diagram of manhole structure

1.1 检查井及井周路面病害类型调查

笔者对济南市新泺大街、天辰路、雪山路、经十东路这4条城市道路检查井及井周路面展开了病害调查,其中新泺大街、天辰路、雪山路各有100处检查井,经十东路有300处检查井。在病害调查过程中,将检查井及井周路面病害分为检查井病害(井盖翘起和断裂、检查井沉陷)、井周路面破损类(路面脱落和坑槽)、井周路面变形类(路面沉陷和拥包)、井周路面裂缝类(路面块状和条状裂缝)这4大类[17],调查结果见表1。

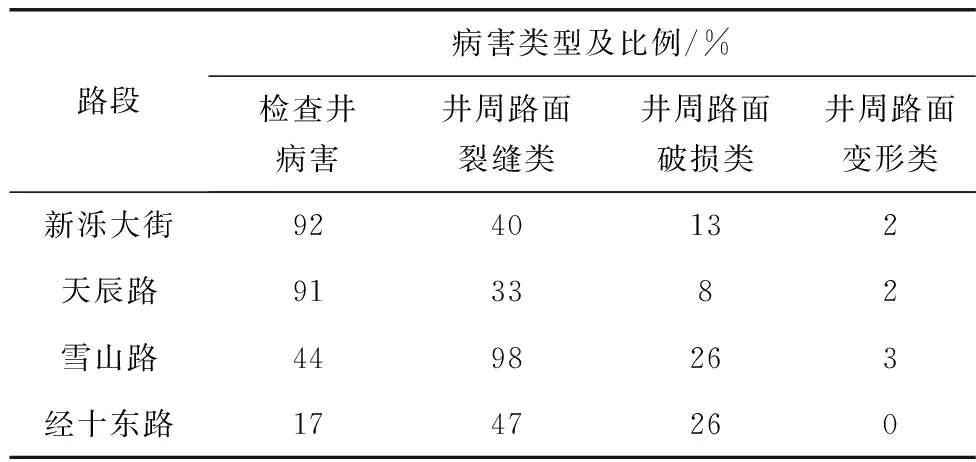
表1 病害类型调查结果Table 1 Investigation results of the disease types

由表1可知:① 这4条道路的检查井病害占比较大,分别为92%、91%、44%、17%;路面裂缝类病害占比相对较少,分别为40%、33%、98%、47%;变形类病害很少,在经十东路中甚至没有。② 各条道路的检查井及井周路面病害往往同时存在多种病害类型,如:新泺大街某处检查井及井周路面既存在检查井病害,也存在裂缝类及破损类病害。

总之,检查井及井周路面病害以检查井病害类为主,破损类病害相对较少,变形类病害极少。因此,在车辆经过检查井及井周路面时,需要考虑检查井振动和变形对车辆荷载动态特性影响。

1.2 检查井及井周路面病害范围调查

以半径为r的圆形区域(包括井盖)表示井周路面病害范围,对这4条道路进行检查井及井周路面病害范围调查。对圆形病害区域利用直尺测量病害区域半径r,非圆形病害区域则测量后计算其面积,并换算成圆形区域[19],病害范围调查结果见图2。

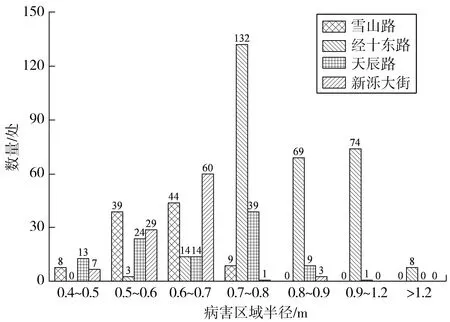
图2 病害范围调查结果Fig. 2 Investigation results of disease scope

由图2可知:这4条道路的井周路面病害区域半径主要分布范围为:雪山路井周路面病害半径92%分布于0.5～0.8 m,经十东路97%分布于0.5～1.2 m,天辰路90%分布于0.4～0.8 m,新泺大街100%分布于0.4～0.9 m。由此可见,井周路面病害半径主要集中于0.4～0.8 m,最大值可达到1.2 m。

2 车辆荷载动态特性

2.1 车辆模型

为便于计算,笔者将18个自由度多质点振动体系的车辆模型进行必要简化[20]。1/2车辆模型在车辆动载特性分析方面是可行的[10-14],故笔者在研究时将车辆经过检查井及井周路面过程分为:车辆从正常路段进入井周路面病害区域→进入井盖区域→进入井周路面病害区域→进入正常路段这4个阶段。

车辆在井周路面上行驶时,路面与车辆的耦合为弱耦合[17],路面振动和变形对车辆振动影响可忽略,故建立5自由度车辆振动模型,如图3。当车辆在井盖区域行驶时,井盖振动和变形对车辆振动影响较大[18],考虑井盖振动和变形,建立车-井盖耦合6自由度车辆振动模型,如图4。相关参数含义见表2。

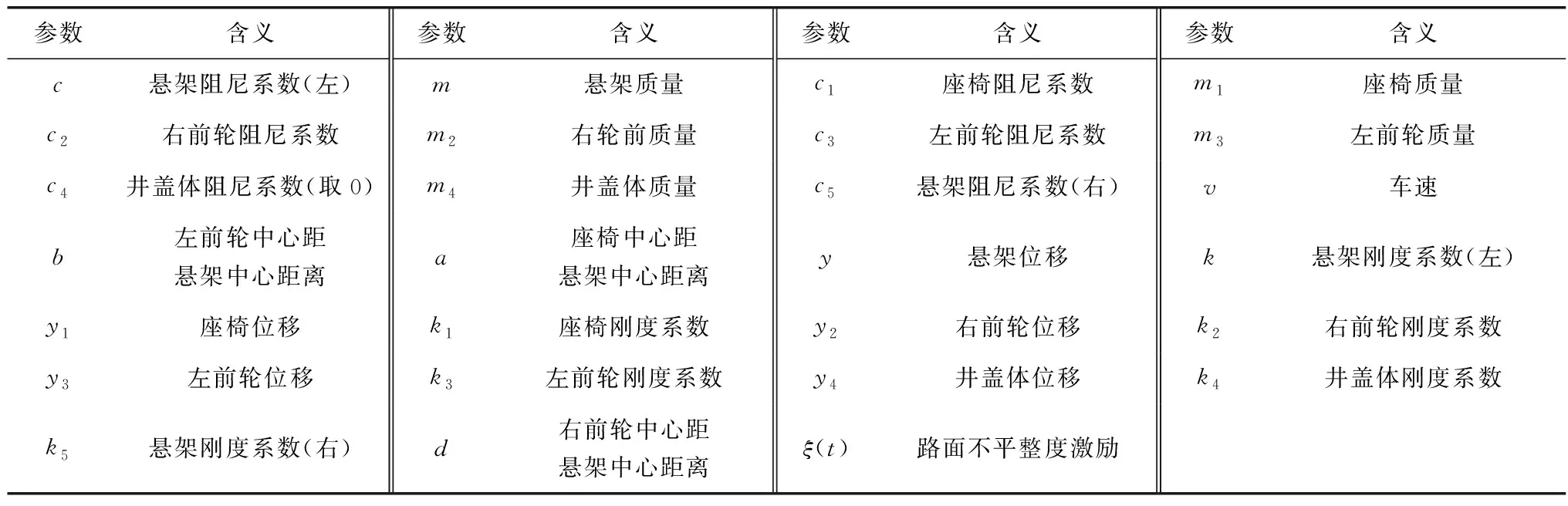
表2 参数含义一览Table 2 List of the parameter meanings

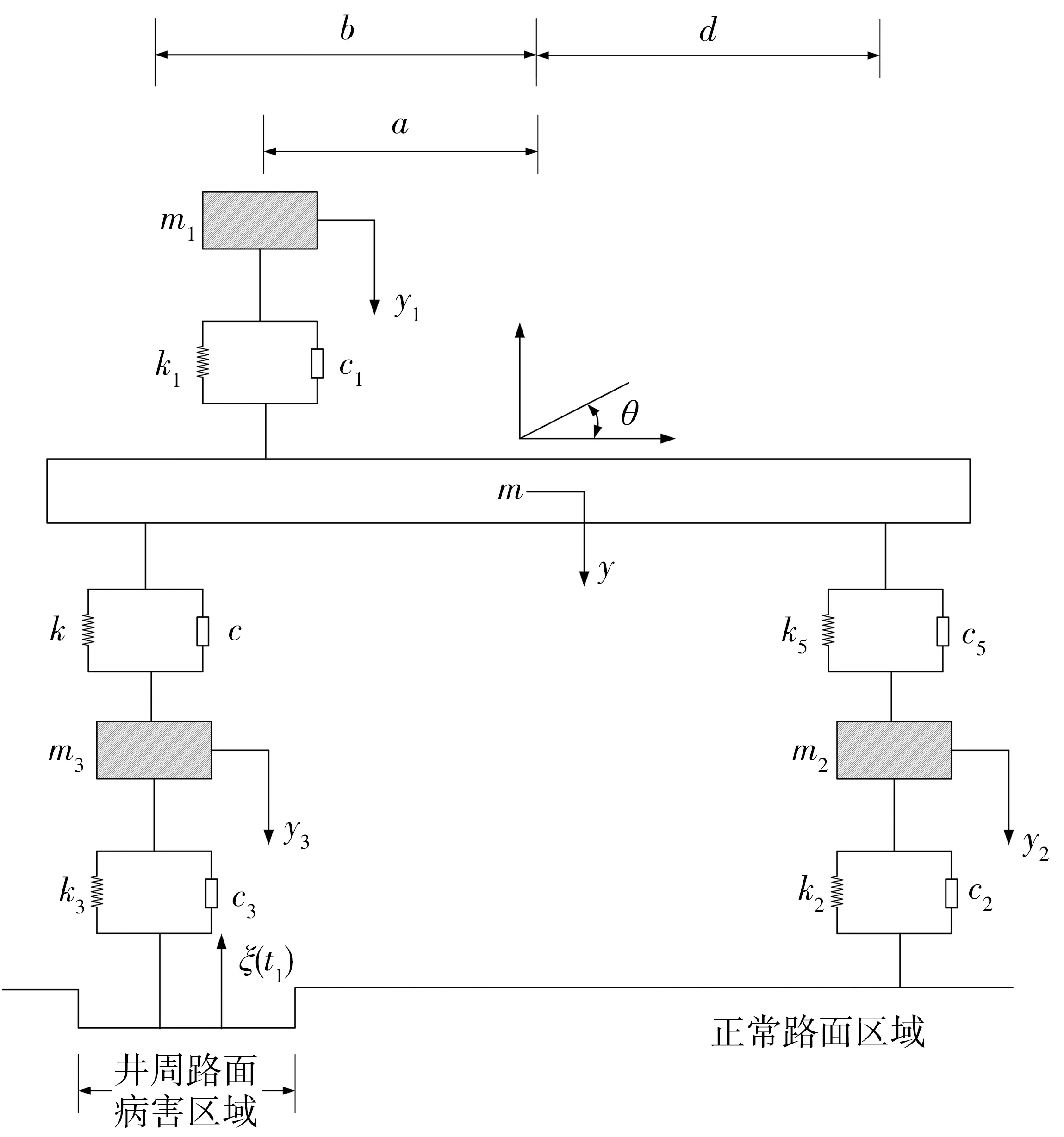
图3 5自由度车辆振动模型Fig. 3 5-degree-of-freedom truck vibration model

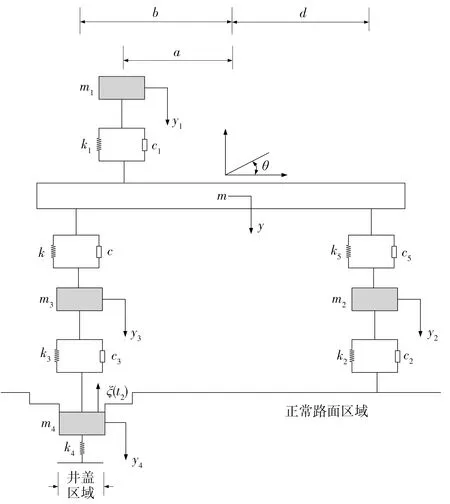
图4 车-井盖耦合6自由度车辆振动模型Fig. 4 6-degree-of-freedom of truck vibration model with truck- manhole cover coupling

在建立的车辆振动模型中,假设井周路面状况良好(除局部病害造成的高差),在初值条件或二次激励条件中将病害作为平整度激励以路面高差形式予以考虑[20]。当车辆在井周路面行驶时,忽略路面振动和变形对车辆振动的影响,建立5自由度车辆振动模型动力学方程[20],如式(1)～式(5)。

my″+k1[(y+aθ)-y1]+k[(y+bθ)-y3]+k5[(y-dθ)-y2]+c1[(y′+aθ′)-y′1]+c[(y′+bθ′)-y′3]+c5[(y′-dθ′)-y′2]=0

(1)

Jθ″+ak1[(y+aθ)-y1]-bk[(y+bθ)-y3]+dk5[(y-dθ)-y2]+ac1[(y′+aθ′)-y′1]-bc[(y′+bθ′)-y′3]+

dc5[(y′-dθ′)-y′2]=0

(2)

m1y″1+k1[y′1-(y′+aθ′)]+c1[y′1-(y′+aθ′)]=0

(3)

m2y″2+k5[y2-(y-dθ)]+k2y2+c5[y′2-(y′-dθ′)]+c2y′2=0

(4)

m3y″3+k[y3-(y+bθ)]+k3y3+c[y′3-(y′+bθ′)]+c3y′3=0

(5)

位移-速度向量有式(6):

Q1(t)=[yy′θθ′y1y′1y2y′2y3y′3]T

(6)

基于式(6),利用传递矩阵法[23]求解式(1)～式(5),可得到位移-速度方程,如式(7)、式(8):

Q1(t)=eA1tQ1(t0)

(7)

(8)

车辆行驶在井盖区域时,考虑井盖振动和变形对车辆振动影响,建立车-井盖耦合6自由度车辆振动模型动力学方程,如式(9)～式(14)。

my″+k1[(y+aθ)-y1]+k[(y+bθ)-y3]+k5[(y-dθ)-y2]+c1[(y′+aθ′)-y′1]+c[(y′+bθ′)-y′3]+c5[(y′-dθ′)-y′2]=0

(9)

Jθ″+ak1[(y+aθ)-y1]-bk[(y+bθ)-y3]+dk5[(y-dθ)-y2]+ac1[(y′+aθ′)-y′1]-bc[(y′+bθ′)-y′3]+

dc5[(y′-dθ′)-y′2]=0

(10)

m1y″1+k1[y′1-(y′+aθ′)]+c1[y′1-(y′+aθ′)]=0

(11)

m2y″2+k5[y2-(y-dθ)]+k2y2+c5[y′2-(y′-dθ′)]+c2y′2=0

(12)

m3y″3+k[y3-(y+bθ)]+k3(y3-y4)+c[y′3-(y′+bθ′)]+c3(y′3-y′4)=0

(13)

m4y″4+k3(y4-y3)+k4y4+c3(y′4-y′3)=0

(14)

位移-速度向量有式(15):

Q2(t)=[yy′θθ′y1y′1y2y′2y3y′3y4y′4]T

(15)

基于式(15),求解式(9)～式(14),可得到位移-速度方程,如式(16)、式(17):

Q2(t)=eA2tQ2(t0)

(16)

(17)

2.2 车辆荷载动态特性

笔者利用车辆荷载冲击系数f来分析车辆经过检查井及井周路面的车辆荷载动态特性。以垂直于路面向下为正方向,车辆经过井盖区域时,记F(t)为车辆动态荷载,如式(18),车辆经过井周路面及常规路面时,令式(18)中y4=0,y′4=0;车辆荷载冲击系数f的计算如式(19)。

F(t)=k[y3-(y+bθ)]+k3(y3-y4)+c[y′3-(y′+bθ′)]+c3(y′3-y′4)+(m+m1+m2+m3)g

(18)

(19)

分析模型参数及确定路面工况条件时,根据文献[24]确定车辆振动模型参数数值,如表3。

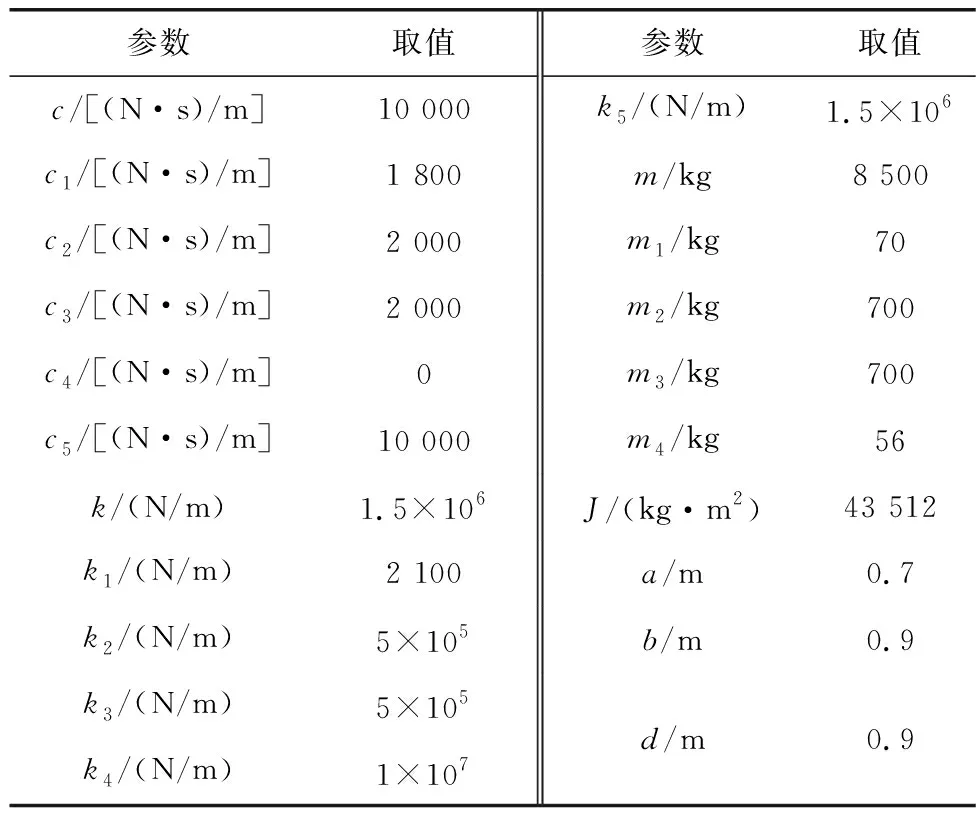
表3 车辆振动模型参数Table 3 Parameters of truck vibration model

当模拟路面工况时,根据病害调查结果以路面下坡方向为车辆行进方向,取车速v=36 km/h,考虑检查井不均匀沉降会导致路面坡度变化,取井周路面坡度变化率φ=4%,井周路面病害范围r=1.3 m,检查井直径为0.7 m,记局部病害导致井周路面出现的高差为H1=1 cm,记检查井沉降导致井盖出现的高差为H2=1 cm。

车辆进入井周路面时,位移和速度初始条件为:y′=0.4,y′1=0.4,y′1=2=0.4,y′3=0.4,θ′=0,y=0.005,θ=0,y1=0.01,y2=0,y3=0.01。

当0.06 s时,车辆由井周路面驶入检查井,位移和速度初始条件为:y4=0,y=y(t1)+0.005,y2=y2(t1),y′=y′(t1),y1=y1(t1)+0.01,y′1=y′1(t1),θ′=θ′(t1),θ=θ(t1),y′2=y′2(t1),y′4=0,y′3=y′3(t1),y3=y3(t1)+0.01。

利用MATLAB求解式(7)和式(15),获得车辆振动模型中任意质量体的速度和位移,进而根据式(16)～式(17)求得车辆荷载冲击系数时程曲线,如图5。

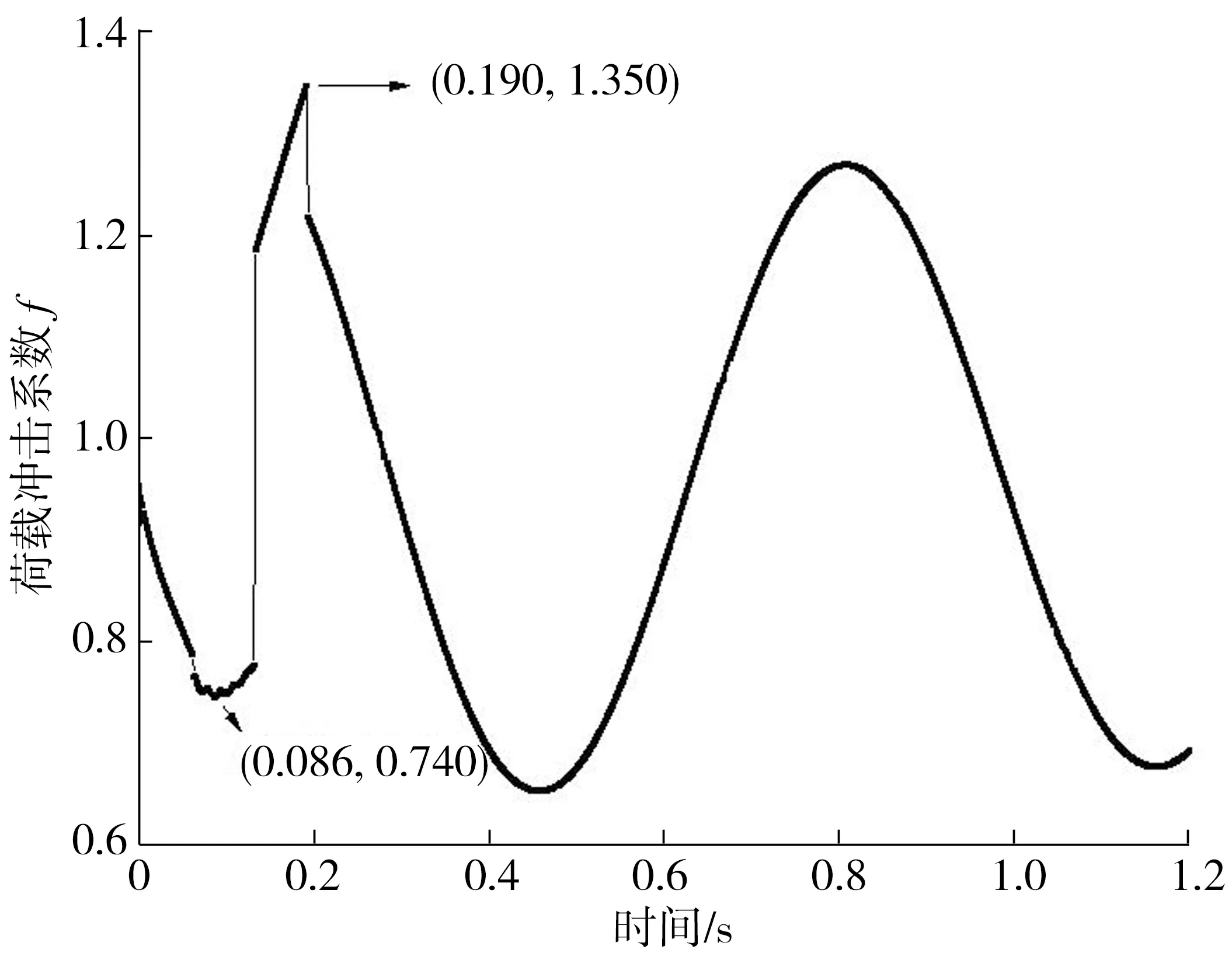
图5 荷载冲击系数时程曲线Fig. 5 Impact coefficient time-history curve of the load

由图5可知:荷载冲击系数在路面高差(平整度激励)作用下,其时程曲线为振幅衰减简谐波,输入平整度激励时,车辆荷载冲击系数产生明显“突变”。当车辆驶入井周路面后,车辆处于下行状态,车辆失重,荷载冲击系数逐渐减小,在0.086 s时到达最小值0.74,此时车辆在井盖上方中心位置行驶;当车辆驶离井盖后,车辆处于上行状态,车辆超重,荷载冲击系数逐渐增大,直到车辆驶离井周路面时到达最大值,即0.19 s时,荷载冲击系数达到最大值1.35。车辆经过检查井及井周路面时,在平整度激励作用下,车辆荷载冲击系数出现最大值,并考虑到井周路基常压实不充分,因此在井周路面产生病害或检查井产生沉降后,井周路面与正常路面结合处荷载冲击效应显著,进而加速井周路面破坏,导致井周路面平整度进一步劣化。

3 影响因素作用程度分析

3.1 荷载冲击系数影响因素

车辆在道路上行驶时,影响车辆荷载动态特性的因素较多,包括车型、轮胎材料组成及型号、行车速度、路面平整度、车辆载重情况等。基于文献[4, 18, 25],考虑悬架阻尼和刚度系数及轮胎阻尼和刚度系数变化较小,笔者重点分析了井周路面病害导致的高差H1、车速v、检查井沉陷量H2、井盖刚度系数k4、井周路面坡度变化率φ等参数对车辆荷载动态特性影响。计算出不同影响因素作用下车辆荷载冲击系数时程曲线,如图6。

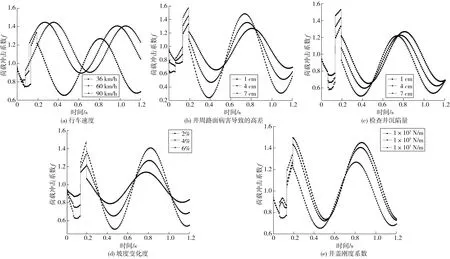
图6 不同因素影响下车辆荷载冲击系数时程曲线Fig. 6 Impact coefficient time-history curve of truck load under different influence factors

由图6(a)可知:荷载冲击系数最大值随着车辆行速度增加而增大,当车辆行驶速度在60 km/h及以上时,荷载冲击系数最大值在车辆于正常路面行驶时出现,荷载冲击系数最大值存在明显滞后效应;当车辆行驶速度由60 km/h增加到90 km/h时,车辆经过检查井及井周路面的时间变短,而振动在车辆垂向的传递时间不变,导致车辆驶离检查井一定距离后荷载冲击系数达到最大,表现出荷载冲击系数最大值存在滞后现象,但荷载冲击系数最大值变化很小,趋于稳定。由此可见,车辆经过检查井及井周路面时提高行车速度,会导致井周路面病害区域不断扩大,平整度进一步劣化。

由图6(b)、图6(c)可知:荷载冲击系数最大值随着H1、H2的增加而增大,图6(b)中车辆驶入正常路面后荷载冲击系数明显大于图6(c)。H1作为车辆振动的激励,高差越大对车辆振动激励作用越强,但井周路面刚度较小,对冲击荷载扩散能力较弱,难以卸载激励输入时产生的冲击荷载,表现出H1对荷载冲击系数影响时间更长;H2作为车辆振动的激励,井盖刚度较大,对冲击荷载扩散能力较强,容易卸载一部分激励输入时产生的冲击荷载,表现出H2对荷载冲击系数影响时间较短。由此可见,H1对荷载冲击系数影响程度远大于H2。

由图6(d)可知:荷载冲击系数最大值随着井周路面坡度变化率增加而增大。在实际工况中,井周路面坡度变化率属于路面病害的“不平整”,在同样的路面平整度激励(井周路面导致的高差和检查井沉陷量)下,坡度变化率越大,车辆垂向作用力分量越大,在同等激励下产生的振动能量越多,表现出路面病害平整性越差,车辆荷载对路面产生的荷载冲击越大。

由图6(e)可知:荷载冲击系数最大值随着井盖刚度系数增加而减小。井盖刚度系数越小,井盖的冲击荷载扩散能力较弱,对荷载冲击系数影响越小。当井盖刚度系数由1×103N/m增加到1×105N/m时,荷载冲击系数变化程度比由1×105N/m增加到1×107N/m时的要小。由此可见:井盖刚度系数越大对减小冲击荷载作用效果越明显。

3.2 各因素影响程度分析

在分析各影响因素对车辆荷载动态特性作用程度时,依据相关性和方差分析过程,以车辆荷载冲击系数最大值为分析指标,对图6中各影响因素进行分析,其结果见表4、表5。

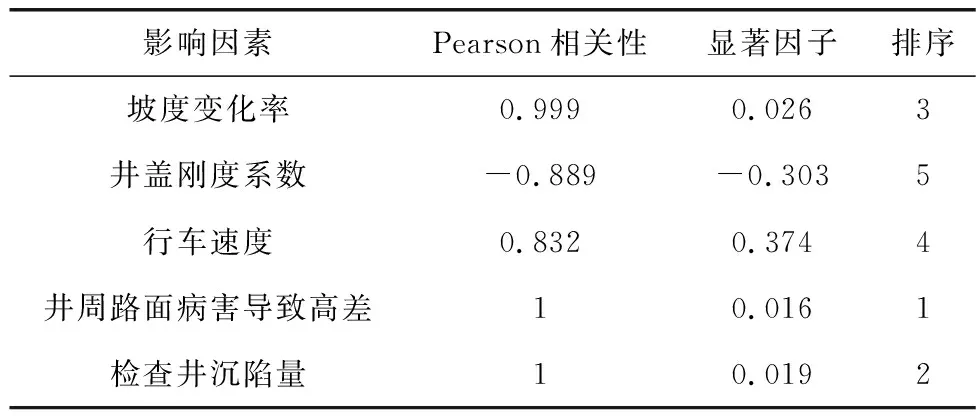
表4 相关性分析结果Table 4 Correlation analysis results

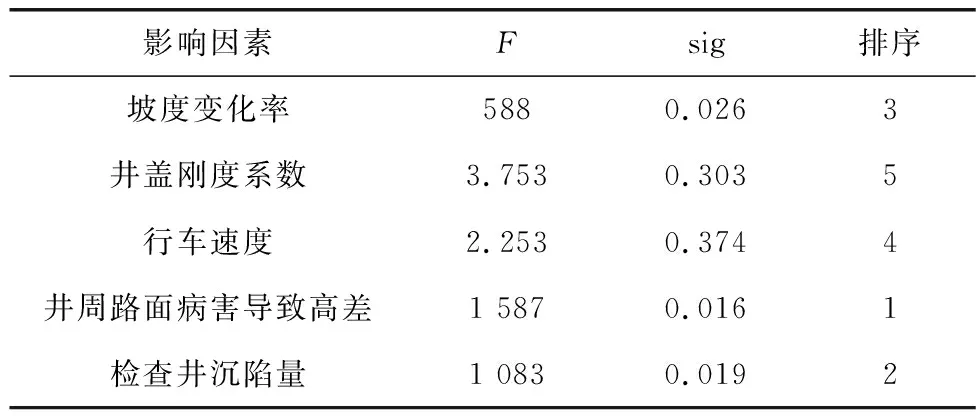
表5 方差分析结果Table 5 Variance analysis results

由表4可知:① 根据Pearson相关性可知,井周路面病害导致的高差、行车速度、检查井沉陷量、坡度变化率对车辆荷载冲击系数的影响呈正相关,根据显著因子进行相关性大小排序为:井周路面病害导致的高差>检查井沉陷量>坡度变化率>行车速度;② 根据显著因子及Pearson相关性可知,井盖刚度系数对车辆荷载冲击系数的影响呈负相关,且有一定显著特征,当车辆经过井盖时,井盖对冲击荷载的扩散作用减小了车辆振动,降低了车辆荷载对路面的冲击。

由表5可知:① 井周路面病害导致的高差、检查井沉陷量、井周路面坡度变化率的sig<0.05,在5%显著水平下对荷载冲击系数最大值具有显著影响,井周路面病害造成的高差、检查井沉陷量和井周路面坡度变化率对车辆荷载动态特性影响较大;② 由F值可知,井周路面病害导致的高差、检查井沉陷量和坡度变化率对车辆荷载动态特性的影响远大于行车速度和井盖刚度系数。

结合图6、表4、表5可知:当车辆经过检查井及井周路面时,各影响因素对车辆荷载动态特性影响程度由大到小排序为:井周路面病害导致的高差>检查井沉陷量>坡度变化率>行车速度>井盖刚度系数。由此可见:路面平整度问题(井周路面病害造成的高差、检查井沉陷量和井周路面坡度变化率)对车辆动载特性影响较大。

4 结 论

1)基于井周路面病害调查结果,根据合理的车辆振动模型及参数,建立了车-井盖耦合振动模型;以荷载冲击系数作为评价指标,当车辆离开井周路面进入正常路面时,荷载冲击系数到达最大值1.35;当车辆经过检查井及井周路面时,由于路面平整度激励作用使得荷载冲击系数最大值增大,加速井周路面平整度劣化。

2)通过相关性分析发现,随着井周路面病害造成的高差、行车速度、检查井沉陷量、井周路面坡度变化率增加,车辆荷载冲击系数同时增大,这就加速了井周路面平整度劣化;随着井盖刚度系数增加,井盖对减小冲击荷载的作用越明显,井盖振动和变形在一定程度上延缓了井周路面平整度劣化。

3)通过方差分析发现,当车辆经过检查井及井周路面时,各影响因素对车辆荷载动态特性影响程度由大到小排序为:井周路面病害导致的高差>检查井沉陷量>坡度变化率>行车速度>井盖刚度系数。检查井沉陷量、井周路面病害造成的高差和井周路面坡度变化率对车辆荷载冲击系数影响最大。由此可见,路面平整度问题(坡度变化率、井周路面病害造成的高差和井盖沉陷量)对车辆荷载动态特性影响较大。