U型波浪结构热沉的流动与热性能分析*

臧鲁浩,王俊超,曹明轩,甘宏海,高一伟

(五邑大学 智能制造学部,广东 江门 529020)

随着储能设备和电子设备的集成化和小型化的发展,相关应用的功率密度和冷却要求也相应提高。高功率半导体激光器(HPLD)是一种典型的高热功率器件,具有占用空间小、系统稳定等特点,在制造领域得到了广泛应用。用于HPLD的传统冷却方法包括自然对流冷却、大通道冷却和半导体冷却。传统的散热方式有着温度不均匀和散热能力不足的缺点,且半导体冷却需要消耗电能,导致产生额外的热量[3]。20世纪80年代Tuckerman团队[4]首次提出微通道散热器(MCHS)来消除设备器件所带来的高热通量。

微通道热沉的流道普遍为直通道,但是有着较大的温度梯度和流体混合不良的缺点[5]。由于单方向流动的特点,在流动方向上流体的流动边界层和传热边界层变厚,增加了整个通道的温差。根据相关研究,将纳米颗粒引入流体以改变其特性和在管内放置干扰单元[11-12]以促进流动混乱都会显著增加传热。然而,修改通道形状以产生二次流来改善传热被证明是更实用、更便宜、更容易在工程实践中实现的[13]。Sui[14]首先提出使用波浪微通道代替直微通道来改善传热效率和温度均匀性。在Sui等的研究之后,许多人尝试实验研究提高波浪微通道散热器的效率[15]。他们的研究结果表明,当液体冷却剂流经波浪微通道时,可以产生迪恩涡,导致混乱的平流,改善冷热流体的混合。迪恩涡会使热力和水力边界层变薄,以加强热传导。

由于激光束组合结构的限制,HPLD的散热器大多采用双层U型MCHS的形式,以确保激光二极管有一个稳定和准确控制的温度工作范围[16]。为了进一步提高激光温度的稳定性,一些研究[17]改变了双层U型通道的结构(弧形、之字形和正弦形),他们发现正弦形的波浪形结构在相同的总流速下,热阻和总压降较小,传热系数较大。然而,目前对双层U型正弦波浪形结构的流动和热特性的研究只做了全局热阻、压降和温度均匀性的研究。并没有评估通道各部分的散热能力,也没有研究正弦波浪形流道单位周期内流体迪恩涡的形成以及结构参数对热特性的影响。

本文为了保证激光器温度的均匀性,使其有一个稳定的工作状态,针对大功率半导体激光器设计了一款通道侧壁为正弦波浪形的双层U型微通道散热器。首先,比较了不同流速下直微通道散热器(SMCHS)和波浪微通道散热器(WMCHS)不同位置(上、中、下段)的平均传热系数(HTC)和热功率,以及热源表面的温度均匀性。其次,研究了在固定泵功率(Ω=0.15 W)下,不同几何参数(波浪形振幅A=30 μm,波长λ=250～1 000 μm)的WMCHS中迪恩涡的变化。最后,比较了不同几何参数(A=50、80 μm,λ=250～2 000 μm)的WMCHS在3种泵功率(Ω=0.05～0.15 W)下的整体热阻、压降、表面摩擦因数和努塞尔数。

1 物理模型和模拟过程

1.1 模型设计

微通道热沉模型如图1所示。图1中A为MCHS的几何形状,其中包括电子元件激光二极管阵列(LDA)形式的热源和一组冷却工质入口和出口。该热沉共有10个微通道,整体尺寸为5.2 mm×12 mm×3 mm(Lx×Ly×Lz)。为了简化计算[18],体积热源被均匀地简化为表面热源。此外,矩形直通道热沉结构具有周期性,为了减少网格大小和计算时间,选择其中一个矩形直通道作为计算域[19](见图1中B)。在这个计算模型中,两个半壁位于微通道的相对两侧。正弦波浪微通道是在本工作中对矩形直通道的基础上改进形成的(见图1中C)。通道波浪的函数为y=Asin(2πx/λ),其中A是振幅,λ是波长。图1中D为单个通道截面示意图。具体尺寸见表1。

图1 微通道热沉简化模型图(A)、SMCHS(B)、WMCHS(C)和微通道剖面(D)示意图

表1 通道结构参数 (mm)

为了研究这个三维模型的热和流动特性并简化问题,使用了如下流动假设:1)热传导和流体流动处于稳定状态;2)通道内流体的流动是不可压缩的;3)固体和液体的热物理特性不变;4)不考虑重力和粘性耗散的影响;5)通过辐射和对流换热向周围空气传递的热量可以忽略。基于上述假设,流体区域的控制方程可表述如下:

∇·(ρU)=0

(1)

∇·(ρUU)=-∇p+∇·(μ∇U)

(2)

∇·(ρcpUTf)=∇·(λf∇Tf)

(3)

λs∇2Ts=0

(4)

式中,p为流体压力;ρ为流体密度;μ为流体粘度;cp为比热容;λf为流体导热系数;λs为固体导热系数;Tf为流体温度;Ts为固体温度。

雷诺数计算如下:

(5)

式中,νin为流体的输入速度;Dh为通道的水力直径。

下面的定义与Zhu研究所用的定义相同,用于确定微通道的平均努塞尔数:

(6)

(7)

Nu=q×Ah

(8)

式中,hm为通道的平均传热系数;Q为热源产生的总热负荷;q为热通量;Ah为热源表面面积;Acon为每个通道的传热面积;Tw为通道壁的平均温度;Tf为冷却液的平均温度,Tf=(Tin+Tout)/2,Tin是冷却液入口温度,Tout是冷却液出口温度;N为微通道的数量。

使用整体热阻和热源表面的温度最大变化量来评估热沉的换热性能,其定义如下:

(9)

ΔTh,max=Th,max-Th,min

(10)

式中,Tmax为热源表面的最高温度;Th,max和Th,min分别为热沉热源表面的最高和最低温度。

下述公式用于计算流体泵功率:

P=V·Δp=N·uin·Ac·Δp

(11)

式中,V为热沉的体积流量;Δp为压降;Ac为通道的横截面积,Ac=HcWc。

下述公式用于计算表面摩擦因数:

(12)

式中,L为通道总长度。

1.2 边界条件

对于通道入口边界条件:

u=uin,v=0,w=0,T=Tin

(13)

对于通道出口边界条件:

p=pout

(14)

流体与固体耦合面的非滑移条件和连续性条件如下:

u=v=w=0,Tf=Ts,kf∇Tf=ks∇Ts

(15)

对于热沉的热源均匀热流密度的条件如下:

(16)

固体的其他表面被认为是绝热的:

(17)

式中,n为流道壁面的法线或对称界面单位向量。

1.3 网格独立性

为了模拟MCHS的热性能和流体流动特性,本文使用基于ANSYS 20.0的商业软件Fluent。热沉模型的材料为铜,冷却液为去离子水。材料的物理特性见表2。流体的入口速度为1.39 m/s,入口温度为295.15 K。为了节省时间和运行内存,本文采用矩形直通道进行网格独立性验证。共采用了4种网格设计,节点数分别为30×107×65、37×150×90、40×165×98和42×180×102。比较了这4种网格布局下热沉的热阻和压降(见表3)。最后,考虑到仿真精度和仿真速度之间的权衡,在后续仿真中选择了Grid Ⅲ。

表2 固体和流体的物理参数

表3 划分网格密度对热阻和压降的影响

1.4 模型验证

为了验证当前模型的可靠性,将仿真结果与Wu等[20]的实验数据进行了比较。在Wu等的实验中,微通道散热器采用铜制成,热源尺寸为10 mm×4 mm,热沉体积为10 mm×5 mm×1.5 mm;入口流量为0.1～0.5 L/min,流量对应的热源功率分别为199.45、209.53、213.14、214.34和215.54 W。Rt随流速变化的模拟数据、参考模拟数据和参考实验数据如图2所示。通过比较,模拟数据与参考模拟数据的平均误差为1.14%,模拟数据与实验数据的平均误差为7.1%,两者吻合较好。

图2 模型验证

2 结果分析

2.1 直通道和波浪通道传热与流动特性

波浪通道的振幅和波长分别为A=50 μm和λ=500 μm,入口流速为1.39 m/s时对比波浪通道和直通道。图3所示为正常工作条件下沿通道壁的局部HTC和通道侧壁热流曲线图。直通道和波浪通道的底部通道的外通道表面和内通道表面的HTC和壁面热流分布相似。当冷却液进入通道时,流动边界层和热边界层在通道内迅速发展。速度梯度和温度梯度的快速下降导致局部努塞尔数相应下降。在进入通道0.5 mm处,HTC下降了一个数量级,热流密度下降的更多,大约有3个数量级。对于直通道来说,在直通道底部侧面的前0.5 mm处,壁面热通量和HTC分布都迅速下降。波浪通道的变化有所不同,在波浪通道底部通道侧面,HTC和壁面热通量分布呈周期性变化。直通道(A)和波浪形通道(B)速度云图如图4所示,从图4可以看到,波浪通道的流动很复杂,在波峰形成的凹穴处产生了迪恩涡。由于扰动的原因导致协同角的减小,这就是波浪通道的HTC和热通量呈周期性变化的原因。图3c中,直通道和波浪通道上通道的平均HTC分别为16 679和20 193 W/(m·K)。此外,这二者的平均热流分别为452 687和461 430 W/m2。当冷却液进入中间通道时,直通道的流动方向发生变化,在底部通道中形成的水力边界层发生了破坏。直通道和波浪通道的中间通道的平均值HTC分别为25 693和29 141 W/m·K。此外,对于直通道和波浪通道,热通量的平均值分别为781 184和743 684 W/m2。直通道的冷却液流入上通道后,流动边界层就开始重建,温度梯度和速度梯度减小,HTC稳定下降,直到冷却液从出口流出。另外,直通道和波浪通道上通道的HTC和壁面热通量分布相同。直通道和波浪通道的上通道HTC的平均值分别为16 297和20 233 W/m·K。此外,二者热通量的平均值分别为518 277和532 112 W/m2。

a) 通道剖面图

b) 外通道壁面HTC和热流分布图

c) 侧通道壁面HTC和热流分布图

d) 内通道壁面HTC和热流分布图图3 直通道和波浪通道壁面HTC和热流分布图

图4 直通道(A)和波浪形通道(B)速度云图

直通道和波浪通道沿流动方向的压力分布贡献比例如图5所示,直通道水流进入中间通道影响了水流的方向,所以中间通道的压降损耗占比最大,为62.1%,底部通道的压降损耗占比为26.1%,上通道的压降损耗占比为11.8%;波浪通道的上通道和下通道压降占比分别增加到31.2%和16.8%,中间通道压降占比降低为52%,主要是因为上下通道为波浪形通道,增加了压降损耗的占比。其中两种通道的下通道压降占比大于上通道,这是因为入水层流动边界层更薄,流速更大,所以其水流的阻力更大。

图5 直通道和波浪通道沿流动方向的压力分布贡献比例

图6所示描绘了热源表面的温度分布。波浪通道的最高温度占热源面面积的37.1%,而直通道的最高温度占73.5%。与直通道相比,波浪通道的温度更低,温度分布更均匀。波浪通道的冷热流体混合均匀,降低了热源的最高温度,并保证了温度的均匀性。

图6 直通道(A)和波浪通道(B)热源面温度分布云图

2.2 振幅和波长对波浪通道的影响

波浪通道热沉的散热性能受多种因素影响,包括波状幅度、波长、波浪线的形状、通道宽度和高度、肋宽度等。幅度和波长是关系到通道散热的两个重要的参数,因此本文在一定幅度和波长范围内进行仿真比较(见表4)。

表4 Case总结

本节仿真结构的截面形状固定为矩形,通道壁厚、通道宽度、高度为固定值,分别为WF=WC=HC=600 μm。固定振幅A=30 μm下热阻RT、热源表面温度最大变化量ΔTh,max、表观摩擦因数f和努塞尔数Nu随波长λ的变化分别如图7～图10所示。图7和图8中,对于正弦波通道,RT和ΔTh,max随着泵浦功率从0.05 W增加到0.15 W显著降低。在泵功率不变的情况下,RT随着λ的增加先显著增加后缓慢增加,ΔTh,max随着λ的增加先增加后减小。值得一提的是,当λ从250 μm增加到750 μm时,可以看到RT急剧增加。有学者[21]研究证明,具有较小波长的波浪形设计可以提供出色的传热性能,从上述分析中可以看出本次的仿真有着相似的规律。从图9可以看出,f随着波长的增加而下降,随着泵浦功率从0.05W上升到0.15W,f急剧下降。因此可以得出结论,和大波长的通道相比小波长通道会使通道内的流体扰动加剧。图10中,当λ变化时,Nu与RT有着相反的变化趋势,Nu随着λ的增加而减小。从上述结果可以分析出,即使ΔTh,max最低,Nu也不一定最高。

图7 固定振幅下热阻随波长的变化

图8 固定振幅下热源表面温度最大变化量随波长的变化

图9 固定振幅下表观摩擦因数随波长的变化

图10 固定振幅下努塞尔数随波长的变化

波长是影响迪恩涡位置和强度的一个重要参数。考虑到入口效应,所以只研究了上通道。图11所示为A=30 μm、Ω=0.15 W时不同波长下波浪通道沿y-z截面的流线和温度云图。对于波长λ=250 μm的波浪通道,上通道长度Lx=4 mm,共有16个正弦波浪单元。考虑到周期性,选择x=2 000～2 125 μm处第9个周期的前半个周期来代表波浪形通道的典型流动。在如下其他波长研究中,也使用相对应的正弦周期单位。

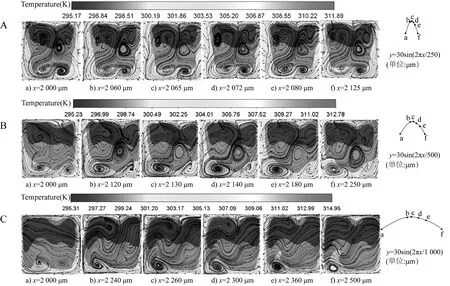
图11 A=30 μm不同波长下波道y-z截面的流线和温度云图

当流体通过弯曲的通道时,流体受到通道壁的曲率中心的离心力,通道中的流体将产生垂直于主流方向的二次回流。由于通道中心的流体流速较高,二次流被分成多个对称部分。在数学上,迪恩涡的产生归因于较高的迪恩数,它与雷诺数和曲率的乘积成正比,临界值为956[22]。图11中,对于波长λ=250 μm的通道,沿主流方向(-x方向),在通道中心和下表面附近出现迪恩涡。此外,迪恩涡的数量和位置在流道上略有不同,涡流的发展始终处于较强的状态。因为通道横截面会产生几对对称、反向旋转的迪恩涡,这些涡流相互支撑。因此,由波长λ=250 μm通道产生的涡流总体上具有较长的持续时间。对于波长λ=500 μm的通道,波峰区域的涡旋尺寸最大,远离波峰区域的涡旋尺寸变小。当波长增加到1 000 μm时,通道内的迪恩涡整体较弱,波峰区域迪恩涡最大。从温度云图的角度来看,低波长通道的流体区域的温度更高,这表明更多的热量被流体带走。从上述分析得出,小波长波浪通道具有产生迪恩涡数量多的特点,使流道内的冷热流体混合更均匀,换热效果更好。

除波长外,振幅也是波浪通道热沉的重要设计参数。不同振幅(A=50和A=80 μm)下热阻RT、热源表面温度最大变化量ΔTh,max、表观摩擦因数f和努塞尔数Nu随波长λ的变化分别如图12～图15所示。图12和图13中,与A=30 μm类似,A=50和80 μm的热阻随λ增加而增加。值得注意的是,A=50和80 μm的热沉在250<λ<750 μm区域的热阻值相近,A=80 μm的热沉在750<λ<2 000 μm的热阻低于A=50 μm的热沉。A=50 μm波浪通道与A=30 μm波浪通道的变化趋势相似,二者都是在λ较大时ΔTh,max处于一个较低的数值。图14中,f随着振幅的增加而增加,而随着波长的增加而减小。图15中,Nu在250<λ<750 μm范围内随着振幅的增大而减小,在750<λ<2 000 μm范围内随振幅的增大而增大,同样幅度下λ=1 000 μm时Nu达到最大值。

图12 不同振幅下热阻随波长的变化

图13 不同振幅下热源表面温度最大变化量随波长的变化

图15 不同振幅下努塞尔数随波长的变化

3 结语

本文对WMCHS和SMCHS在相同工作条件下的流动和传热特性进行了模拟和比较。当进口速度固定为1.39 m/s时,WMCHS侧表面的局部HTC和热通量都高于SMCHS。WMCHS通道的波峰形成的凹穴处产生迪恩涡,使流体更好地混合,增强了局部换热能力。在WMCHS的流动方向上,上段和下段的压降增加,总压降比SMCHS的高26.5%。在WMCHS中,热源表面的温度是相对均匀的。小幅度波浪通道的波长越小,散热效果越好。因为小波长增加了对流传热面积,产生的涡流数量多,发展较强,从而提高了散热器的传热性能。此外,f随着振幅的增加而增加。由于振幅增加,曲率半径增大,流体的扰动更加剧烈。当波长λ=250 μm时,小振幅(A=30 μm)WMCHS中的迪安涡旋持续时间最长,努塞尔数(Nu)达到最大值。当振幅A>80 μm时,Nu在波长接近1 000 μm时增加到最大值。