城轨过渡时段列车运行图调整方法

吴学良，王伟，彭浩，王志凯，谢辉，曹驰

（1.北京市地铁运营有限公司，北京 100044；2.交控科技股份有限公司，北京 100070；3.北京交通大学 电子信息工程学院，北京 100044）

0 引言

为满足市民日益增长的出行需求，缓解交通矛盾，城市轨道交通得到了快速发展。与其他交通方式相比，城市轨道交通具有安全可靠、速度快、密度大及乘车环境舒适等特点，目前已经成为市民选择出行的主要交通方式之一。

在实际运营过程中，城轨运营公司一般会根据客流需求并结合运营成本提前做好行车组织工作并编制列车运行图，确保列车安全有序地开行。但城轨是一个复杂巨系统，在运营的过程中难免会出现如车门故障、线路阻塞等复杂因素的干扰。运营干扰通常会导致某个或者多个列车产生延误，导致原计划不可行。为减小延误对运营和乘客造成的负面影响，需要对列车运行图进行调整［1］。

目前，城轨调度员调整运行图的目标是从运营公司的角度考虑，使线路上的列车尽快按照计划运行图运行，同时减少列车延误，提高运行图兑现率，但这种调整目标存在一定的缺陷。由于城轨客流分布具有显著的时间不均衡特性，城轨运营公司为了节约运营成本通常根据客流量的大小将全天的运营时段划分为高峰和平峰时段。高峰时段线上运行的列车多，发车间隔小，运力充足。相反地，平峰时段运行的列车少，发车间隔大，运力较小。在高峰到平峰过渡阶段若有列车发生延误，则会导致高峰时段的乘客在站台滞留。如果调度员继续调整运行图使列车按照计划运行，会导致运力不足，使原本滞留的乘客无法被服务，降低了乘客服务质量。因此，调度员在运行调整时应当综合考虑运营公司指标和乘客服务质量，寻求二者的平衡关系。

以最小化站台滞留乘客、取消车次数量和运行图偏移为优化目标构建了优化模型，该模型考虑加开临时客运车次（简称加开临客）的调度策略。利用线性化手段将模型中的非线性约束线性化，进而将模型转化为混合整数规划模型，最后利用CPLEX 求解器求解模型。通过仿真案例验证模型能够在减少滞留乘客的同时尽快恢复正常的列车运行秩序，模型的目标最小化站台滞留乘客数量能够在一定程度上指导运营公司提高乘客服务质量。

目前，关于城轨调度的研究按照目标可以分为以下两类：（1）乘客服务质量；（2）运营公司成本及服务质量。与乘客服务相关的指标包括：乘客等待时间、乘客旅行时间、车厢满载率等。Barrena等［2］研究了铁路列车晚点条件下的运行图调整问题，构建了2个非线性数学模型以最小化乘客在车站的等待时间，并提出一种近邻搜索算法来提高求解速度。Gao 等［3］研究了城轨中断恢复后的列车运行调整问题，以最小化滞留乘客数量为目标构建了混合整数规划模型，并设计一种基于分解的迭代式启发算法求解模型。

与运营公司成本及服务质量相关的指标包括：列车运行能耗、列车延误、取消车次数量等。D’Ariano等［4］提出利用比选图和人工变量“大M”表示轨道交通网络中列车运行的闭塞区间占用过程，并设计了基于分支定界和启发式分支规则的求解算法，该方法可以在较短的时间内得到精确的最优解或者近似最优解。Lamorgese 等［5］提出了面向列车延误最小化的基于jobshop 的铁路列车时刻表调整模型。研究采用Benders［5］分解方法重新建模，改进了传统采用“大M”变量的job-shop 方式。Wang 等［6］考虑了可用车底数量约束，以时刻表偏差、取消车次数量、追踪间隔变化为优化目标，建立了一个复杂的混合整数规划模型，提出两阶段求解算法从而提高计算效率。

近年来也有一些学者将2 个目标综合考虑。Zhan等［7］利用时空网络模型，建立了列车调度和乘客路径优化的综合问题。研究使用交替方向乘子算法（ADMM）将该模型分解为列车调度问题和乘客路径问题2个子问题，之后进一步分解为一系列列车或乘客的最短路径问题，并用动态规划算法求解。Zhu 等［8］针对中断场景提出了一种运行图调整模型，将灵活停站和灵活中途折返与其他调度措施结合，该模型的目标是尽量减少乘客延误。

1 列车运行图调整模型

1.1 问题描述

研究案例为一条典型的单线双向城市轨道交通运营线路，其线路拓扑结构示意见图1。为了方便表述，将车站站台简称为车站。线路中的终点车站提供折返线供上下行列车换端并改变运行方向，同时实现上下行车次的车底衔接。线路中的车辆段中提供存车、检修的场地，列车可以直接从车辆段出库或返回车辆段存车。

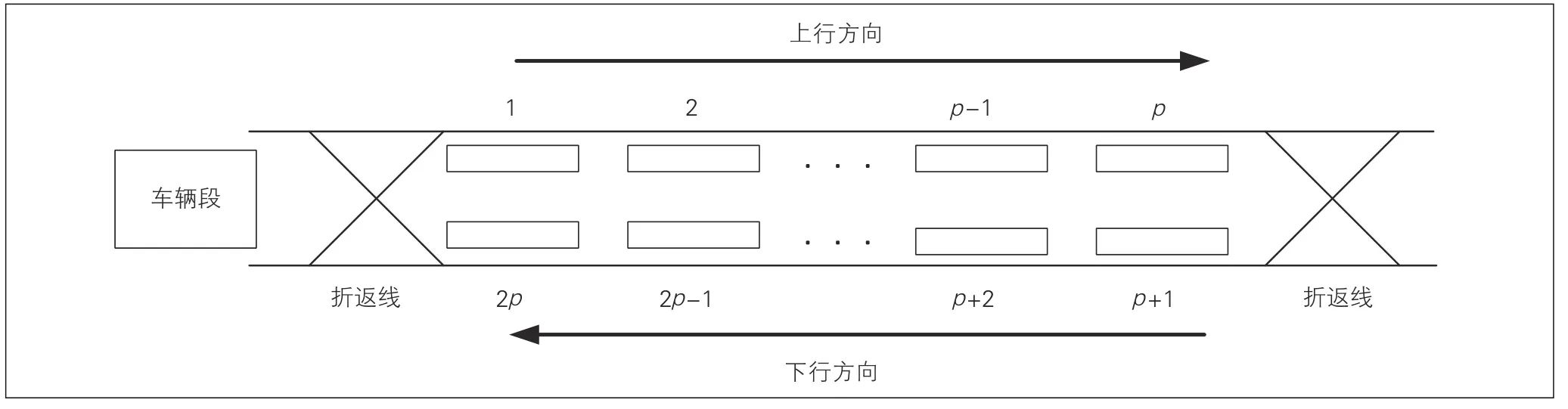
图1 城轨线路拓扑结构示意图

为了方便建模，提出基本模型假设如下：

（1）假设所有列车都按照规定的次序运行，运行过程中不考虑越行或会让的情况。在以往很多城轨运行调整文章中都有类似的假设［9-10］。

（2）为保证乘客服务质量，假设所有列车经过车站时都必须停车，即不考虑车站跳停的情况。

（3）研究未考虑到OD 客流，所以列车到达各个车站时的容量无法确定。为简化模型，认为列车到达后，从车站乘坐该列车的乘客数量是有限的。

（4）由于城轨线路不同方向上存在不同的客流特性，因此假设开行的临客车次运行至终点站后直接进入车站存车线或车辆段，不再折返开行其他车次。

1.2 符号定义

（1）集合及参数符号定义见表1。

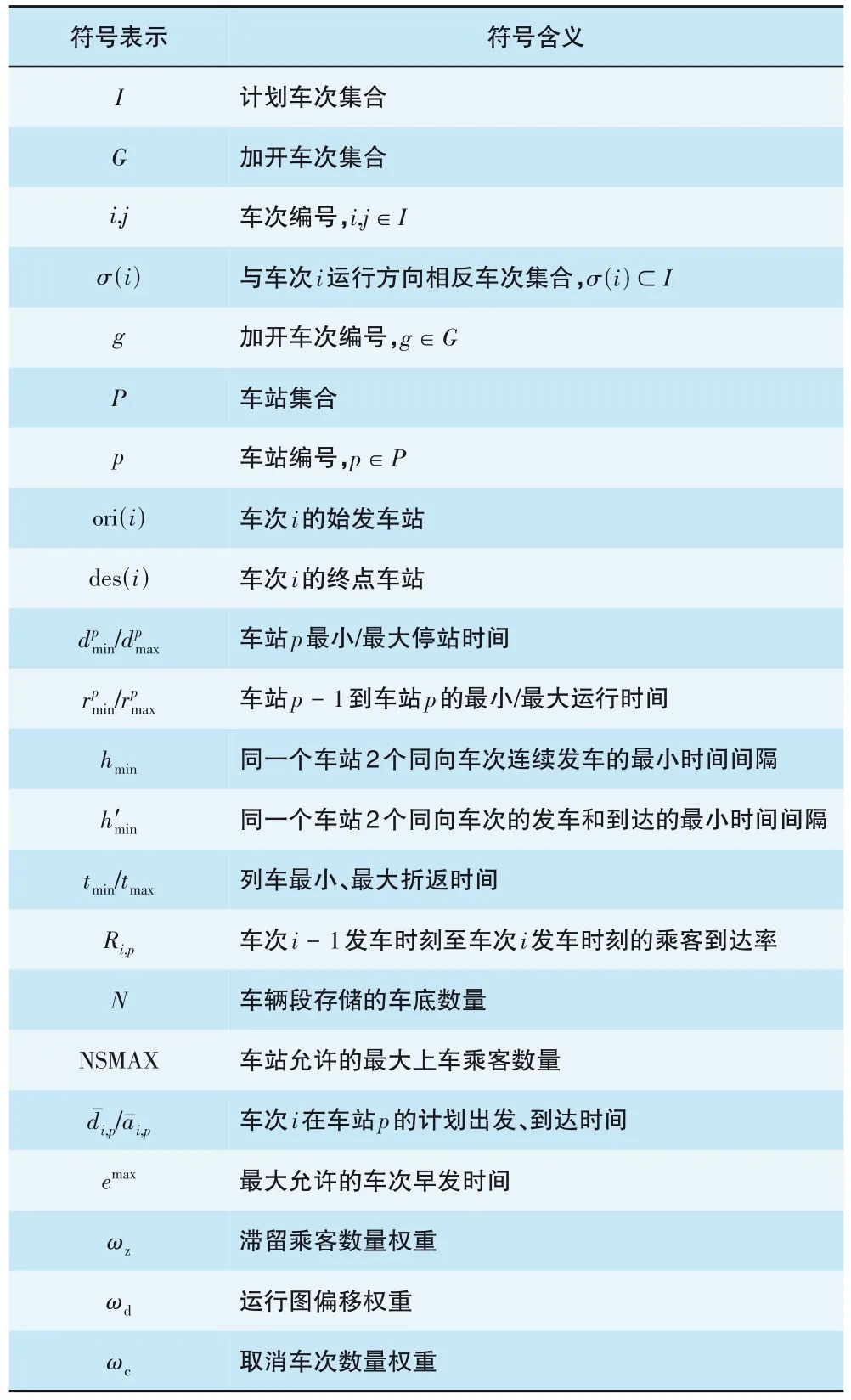
表1 集合及参数符号定义

（2）决策变量定义见表2。

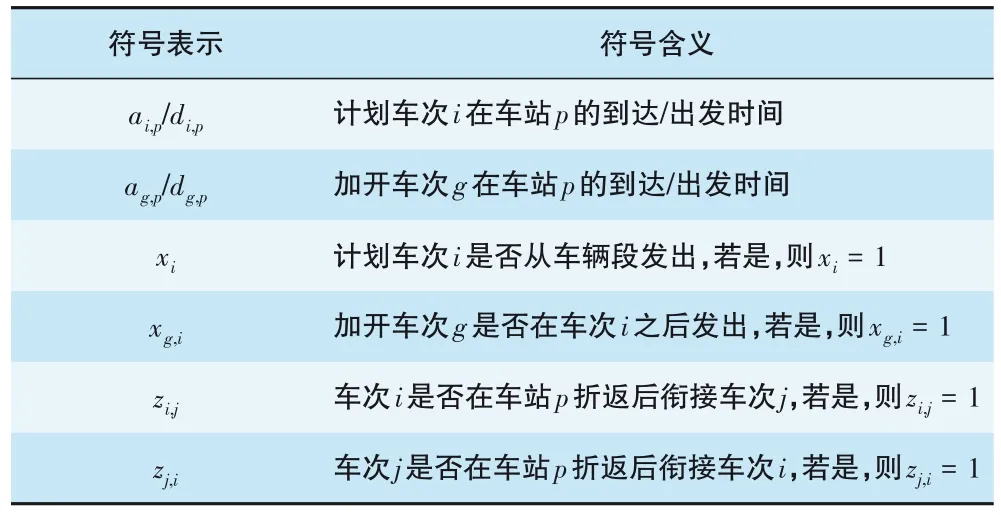
表2 决策变量定义

（3）中间变量定义见表3。

1.3 目标函数

研究一种在高峰向平峰过渡时段列车发生延误情况下的列车运行调整方法，构建了综合考虑乘客服务质量、列车延误和取消车次数量的城轨列车运行调整模型。

（1）车站滞留乘客数量。车站滞留乘客数量和加开车次的滞留乘客数量为：

将所有车次在所有车站的滞留乘客数量求和：

（2）列车延误。定义列车延误为：

式中：|ai，des(i)-，des(i)|为车次i在其终点站的到达时间与计划到达时间的差值绝对值；|di，ori(i)-，ori(i)|为车次i从始发站发车的时间与计划发车时间的差值绝对值。

将所有计划车次的延误时间进行求和，得到：

（3）取消车次。取消车次数量为：

定义目标函数权重参数ωz，ωd，ωc分别表示滞留乘客数量、运行图偏移和取消车次数量的权重，研究构建的模型目标函数为：

在定义上述目标时均引入了非线性表达式，以下将通过线性化手段将它们转化为线性表达式。

1.4 约束构建

（1）若车次i的服务在车站p被取消，那么令该车次在车站p的发车时间为0：

式中：M为一个充分大的正数；当ci= 1，由于M充分大，上面的约束自然成立；当ci= 0时，di，p= 0。

（2）为了保证正常的乘客乘降作业，列车在车站的停站时间必须大于最小值dmin：

（4）同方向的连续2个车次在同一车站的发车和到达时间必须大于最小值h′min：

（5）同方向的连续2个车次在车站的发车间隔必须大于一个最小值，用hmin来表示连续2 个车次的发车间隔约束：

（6）列车需要利用折返线来改变运行方向，列车折返需要满足一定的折返时间约束：

（7）一个车次折返后只能衔接一个反向的车次，每一个车次也只能由另一个反向的车次进行衔接，约束表示为：

（8）若车次没有车底执行则会被取消服务。一个车次在某车站是否有车底执行取决于2个方面，必须有反方向的车次在终点站折返后开行该车次或者由车辆段中的车底直接开行。否则该车次在该车站的服务将被取消。上述条件可以由以下表达式进行约束：

（9）为了保证乘客服务质量，车次到达车站的间隔不应过大，规定不能连续2个车次取消服务，从而保证了各个车站的服务频次，约束保证为：

（10）在实际运营中，从车辆段发出的车底数量应该小于等于车辆段初始的存车数量，约束保证为：

（11）在实际运营中，车次在各个车站的提前发车时间一般不得超过一个固定的阈值，用符号emax来表示最大允许的早发时间，并定义约束为：

（12）加开车次约束。对于加开车次来说，其本身需要满足式（7）—式（12）这几类约束。此外，由于加开车次的次序和计划车次的次序不确定，因此需要增加加开车次和计划车次的追踪间隔约束：

（13）乘客乘降约束。首先计算乘客等待人数：

式中：nwi，p表示在车站p等待乘坐车次i的乘客数量。

式（20）是一个取最小值的表达式，左边项即ci，p⋅M表示若车次i取消，则等待上车人数为0。右边项表示在车站p等待乘坐车次i的乘客数量等于在车站p等待乘坐车次i- 1 的乘客数量减去实际乘坐车次i- 1的乘客数量nsi-1，p，加上车次i之前车次的发车时刻至车次i发车时刻到达的乘客数量，最后减去乘坐加开车次g的乘客。mi，p计算公式如下：

如果车次i在车站p取消服务，那么mi，p就等于车次i之前第1 个没有取消的车次发车时间，否则mi，p等于车次i在车站p的发车时间。

计算车站上车人数，车站p乘坐车次i的乘客数量是等待人数和最大上车人数的最小值：

至此，列车运行的基本模型构建完毕。在模型的构建过程中，部分约束引入了二次项导致模型非线性，为方便求解，必须将约束线性化。

2 模型线性化方法

构建列车运行约束时引入了大量非线性约束，为了方便求解，采用线性化方法将模型转化为整数规划模型。下面针对模型中典型的非线性结构介绍其对应的线性化方法。

（1）min 函数线性化。以上车人数约束为例进行线性化。nsi，p= min{nwi，p，NSMAX}可以改写为：

（2） max 函数线性化。以表达式mi，p=max{di，p，mi-1，p，dg，p⋅xg，i}，i> 1 为例进行说明，该表达式可以由下面的线性约束进行替换：

（3）绝对值函数线性化。在计算列车延误时引入绝对值和二次项表达式devi=(|ai，des(i)-，des(i)|+|di，ori(i)-，ori(i)|) ⋅ci，i∈I。为了将该表达式中的绝对值函数线性化，首先定义辅助变量ui，p，vi，p并添加约束如下［11］：

上面的约束将绝对值表达式转化为4 个线性约束，此时原表达式可以等价改写为：

3 仿真验证

为了验证提出模型的有效性，设计仿真案例进行验证分析。考虑一个典型的城轨线路，线路中有5个车站，每个车站有上下行2 个站台。为了方便出车和回库，在上下行的终点站各设置1个车辆段。选取上下行各15 个车次，上下行前10 个车次保持180 s 的发车间隔，后续的5 个车次按照360 s 间隔运行。下面将针对不同的参数设置进行仿真验证。

（1）以最小化运行图偏移和取消车次数量为目标的运行调整方式。设置权重参数ωz= 0，ωd= 1，ωc=300，选取不同的故障车站进行仿真验证，每个案例设置故障时长300 s，仿真结果见表4。

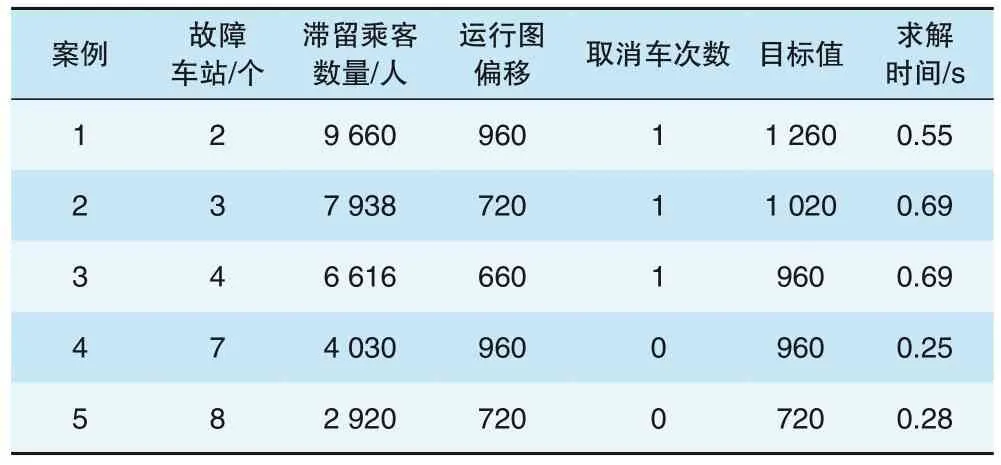
表4 以最小化运行图偏移和取消车次数量为目标的运行调整方式仿真结果

案例1—案例3 为上行车次9 故障，案例4—案例5为下行车次9故障，为更直观地显示运行调整效果，绘制了案例2中的列车运行图（见图2）。

（2）以最小化滞留乘客数量为目标的运行调整方式。设置权重参数ωz= 1，ωd= 0，ωc= 0，选取不同的故障时长和故障位置进行仿真，仿真结果见表5。

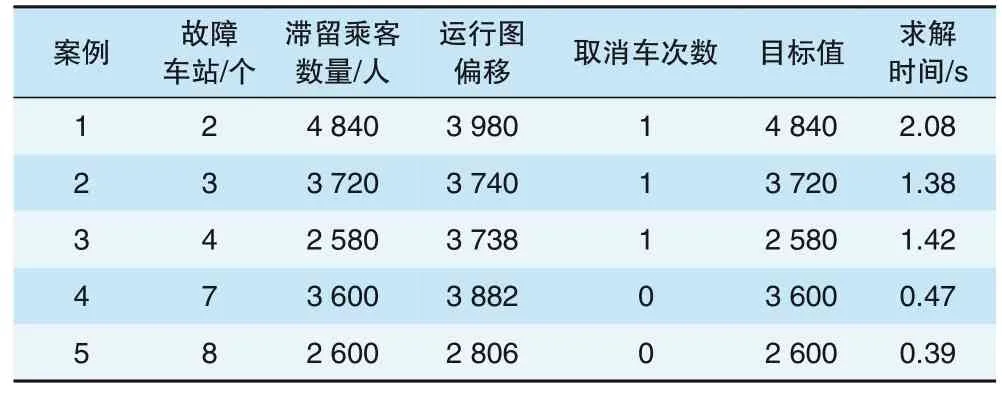
表5 以最小化滞留乘客数量为目标的运行调整方式仿真结果

对比表4、表5 的计算结果可知，表5 的滞留乘客数量相比于表4 的结果大大减少，但运行图偏移较大，这主要是由于目标函数权重的设置不同导致的。接着，绘制表5中案例2的运行调整结果见图3。

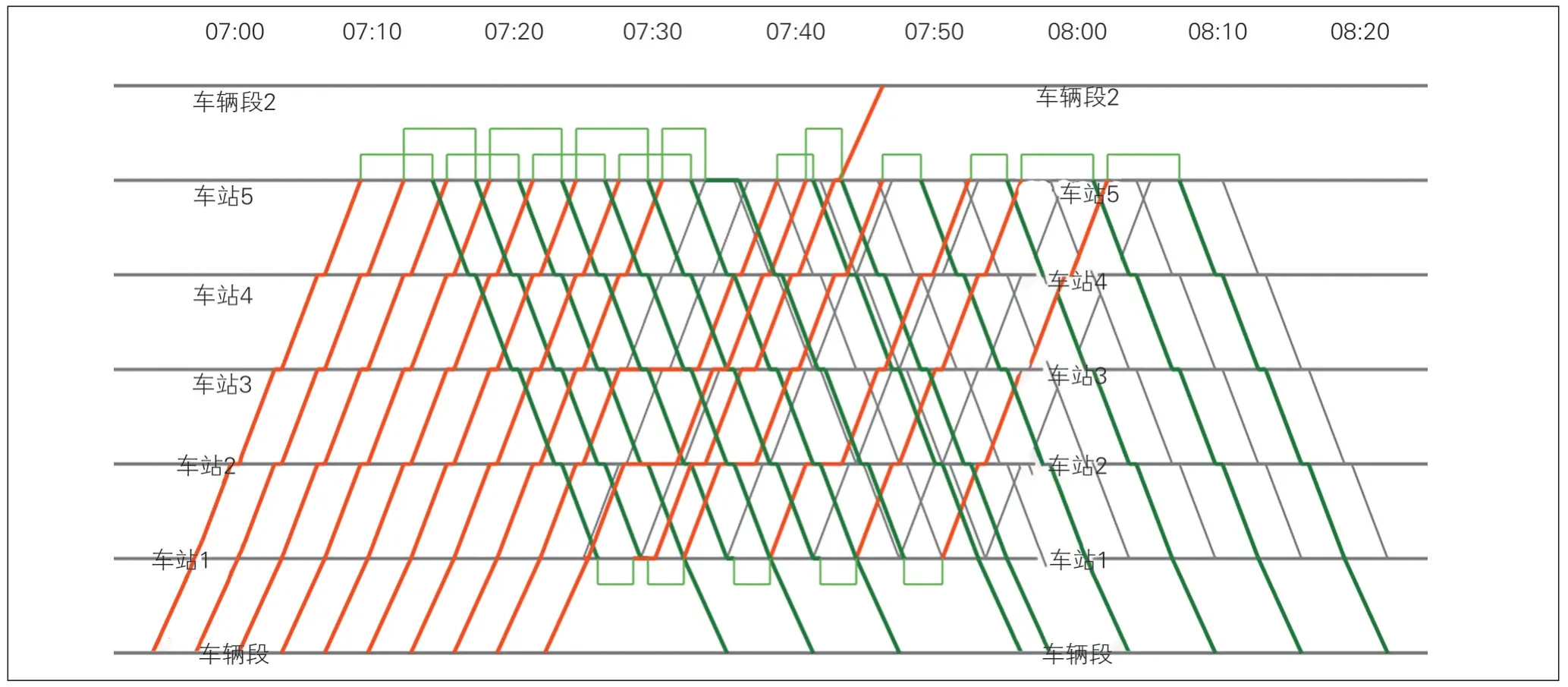
图3 以最小化滞留乘客数量为目标的运行调整结果（上行车次9在车站3故障300 s）

（3）综合考虑乘客服务与运营指标的调整方式。采用综合考虑滞留乘客数量和运营指标的调整方式，设置车站3 为故障车站，上行车次9 为故障车次，选取不同的权重参数进行仿真，与上面的2 组实验进行对比，计算结果见表6。由表6 可知，随着滞留乘客数量权重的增加，优化得到的滞留乘客数量随之减少。因此，调度员在调整运行图时应当根据实时运行状况采取不同的调整手段。例如在滞留乘客数量较多时，增加有关乘客服务的权重，及时服务车站滞留乘客，反之则增加运行图偏移和取消车次的权重。

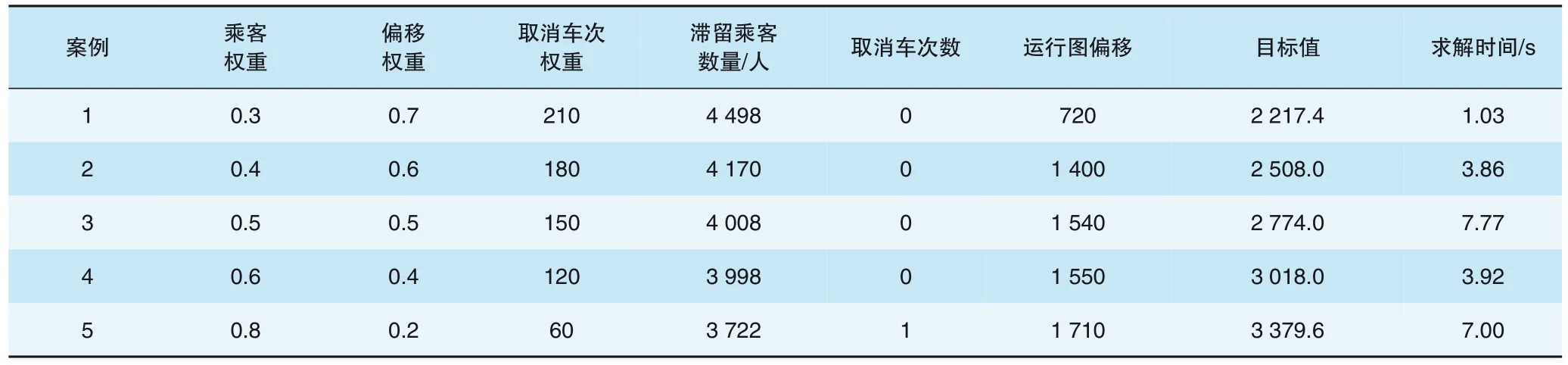
表6 综合考虑运行图偏移、取消车次数量和滞留乘客数量的运行调整方式仿真结果

（4）考虑加开临客的调度策略。研究加开临客策略对运行调整结果的影响，在上行方向增加1个临时客运车次，研究不同故障车站对仿真结果的影响。目标函数权重设置为0.5∶0.5∶150，计算结果见表7。对比表1 和表2 的计算结果可以发现，加开车次后，滞留乘客的数量大大减少了，验证了加开车次策略的有效性。

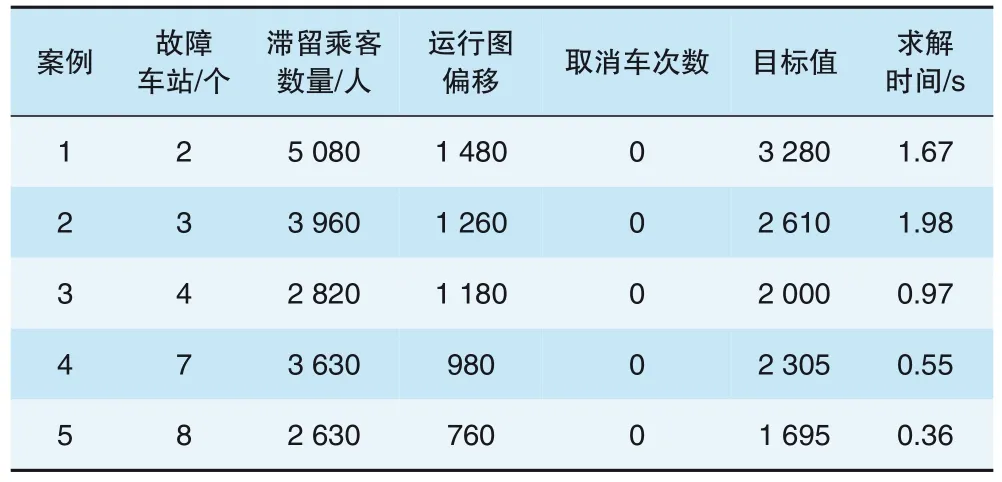
表7 考虑加开车次调整措施的运行调整仿真结果

4 结论

以城轨高峰到平峰过渡时段发生列车延误为场景，综合考虑运营公司指标以及乘客服务质量，以最小化列车延误、取消车次和车站滞留乘客数量为目标函数构建了城轨列车运行图调整模型。为了提高故障的恢复效率，该模型考虑了加开备车的调度策略，利用线性化手段将目标和约束中的非线性表达式线性化，从而将模型转化为混合整数线性规划模型。为了验证模型的有效性，设计了仿真案例进行验证。通过CPLEX求解器求解模型，结果表明提出的运行调整方法能够在恢复运营秩序的同时有效减少过渡时段因列车延误导致的滞留乘客数量，为运营公司提高乘客服务质量提供良好的支撑。在未来的研究过程中，可以进一步考虑乘客OD数据。