小学生数学说题的内涵和结构分析

林祎珣

（福建省厦门市集美区后溪中心小学，福建 厦门 361021）

数学是一门比较抽象的学科，对于大部分小学生来说学好数学还是有难度的，具体体现在以下方面：首先是概念的掌握上，比如周长、面积、体积的概念，对于不同程度的孩子们来说掌握起来是天差地别的；其次是体现在听课效果上，部分孩子课堂上好像听懂了理解了，但是一到做作业又什么都不会了；再次是知识遗忘和混淆，比如分数和百分数的联系和区别；最后是各种常见错误，比如单位换算、计算失误、少算漏算等。开展小学生数学说题活动，通过说审题、说思路、说答题、说反思等，引导小学生从解题走向析题、说题，从而让解题思维看得见，解题策略听得见，让深度学习真发生。

一、小学生数学说题的内涵

学生说题，是指学生生在认真做题，精心准备后说出自己对数学题目的认识与理解，阐述习题解答时所采用的思维方式，解题策略、方法及依据，进而总结出经验性的解题规律。学生说题不是对解题过程的简单叙述，而是在说题做题的过程中把新知识弄懂学会，与原有知识融会贯通，举一反三，提升学生的思维品质和数学素养。因此，在开展小学生数学说题活动的过程中，应注意以下三点：

（一）先解题后说题

学生说题必须先会解题，说题所花的时间比解题更长，而学生能够花在数学学科上的学习时间是有限的，是非常宝贵的，所以教师应该仔细分析教材例题和教辅习题和经典考题，教学过程中要精心选择典型题目作为学生说题的素材。

（二）挖信息简过程

数学题目往往是灵活多变的，有些方法用起来运算量大且复杂易出错，学生说题时，教师要注意引导学生充分挖掘题目中的信息和数量关系，选择合适的方法，可以通过说一题多解，对不同解法进行对比，初步引导学生体会“信息挖掘越充分，解答过程越简洁”。

（三）重联系学新知

数学知识的学习环环相扣，新学的知识与学过的知识之间不仅有知识间的联系，还有方法上的联系。比如五年级所学的“分数的意义和性质”以三年级学过的“分数的认识”为基础，长方体体积公式的推导过程和三年级学过的长方形的面积公式的推导过程类似，长度、角度、面积、体积测量的本质都是一个个计量单位的累加等等。所以我们要注重联系，引导学生回忆，并“说”出已经学过的知识。

二、小学生数学说题的结构框架

本文以数学解题的相关研究和深度学习理论为基础，结合上文内容分析，总结出学生说题的四个环节,分别为：说审题分析、说解题思路、说解题步骤、说回顾反思。接着，根据义务教育数学课程标准中的课程内容和学业质量要求，我们将学生说题的四个环节再细分13 点，构建学生说题的结构框架如图1 所示。

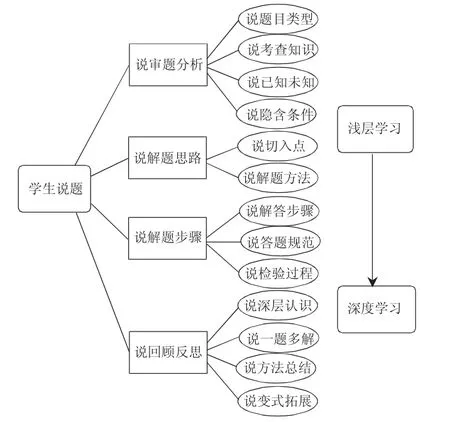
图1 学生说题结构框架

（一）说审题分析

弄清题意是正确解题的前提，也是有效说题的保障。许多小学生由于年龄小玩心重，答题只追求速度，经常没有看清题意就开始解答，今天上课老师教了“分数乘法”，那么今天的所有题目一律用“乘法”来解决，一下就掉陷阱了。如果是说题，那么就得“逼着”自己好好审题了。审题分析可以从题目类型、考查知识点、已知未知、隐含条件四个方面来说。

下面主要从考查知识点和隐含条件两方面展开。

1.说考查知识

说考查知识也就是说出题目所要考查的核心知识点以及相应的数学方法，包括概念、公式、算理、算法、推理方法等。我们常说“万变不离其宗，以不变应万变”，意思就是题目再怎么变，考查的还是那些核心的知识与方法。

2.说隐含条件

能否挖掘出题目中的隐含条件往往关系到能否正确解题。说隐含条件时，可以说一说由已知的显性的信息可以得出哪些结论，题目隐藏着哪些限制性条件（如单位是否需要换算，求现实生活中物体的表面积时求几个面等），题目信息，比如文字语言、数量关系（这个条件怎么用数学符号或式子表达）等。

“说审题”案例分析：

题目：明明拿来两个长度相同的长方形纸条按图2 放置，现在将这两个长方形同时向左右方向平移至图3，相交部分和未相交部分的比是4:5。再平移至图4，相交部分是未相交部分的,现在图4 两个长方形纸条总长是多少厘米？

图2

图3

图4

说题目类型和考查知识：这是操作中的数学问题，考查的是应用比的知识解决问题，培养学生的观察能力、计算能力和空间想象能力等。

说已知未知：题目已知的数学信息为“第一次平移后相交与未相交部分的比是4:5，总长72 厘米”，“第二次平移后相交与未相交部分的比是3:10”，未知的信息是“一个长方形纸条的长度”。

说隐含条件：本题求的是第4 图两个纸条的总长度，隐含着的条件其实是重叠部分一样，空白部分也一样。此外，还有一个隐含问题就是“每个长方形纸条的长度是多少？”从图3 中的72 厘米对应4:5，可以分别求出未相交和相交部分的长度，未相交部分的一半与相交部分的和就是一个长方形纸条的长度。

（二）说解题思路

说解题思路就是指说分析与解答的过程，分析已知条件和未知条件之间的等量关系，采用适当的数学方法得出问题的“解”，题目的解题思路可以从切入点和解题方法两个方面来说。

1.说切入点

说解题的切入点，就是要说清楚是如何提取题目中的有用信息，理解关键句，找到问题的突破口的。

2.说解题方法

小学数学中，常见的解决数学问题的方法有分析法、综合法、联想法、归纳法和假设法，这些都是体现一般思维规律的方法，适应面较广。另外，还有一些适应面较窄的作答技巧，比如解答选择题时经常采用的排除法和代入法。

“说解题思路”案例分析：

题目：下面是六块玻璃，用它们做一个鱼缸，底面选用（），左右两侧选用（）、（），前后两面选用（）、（）。这个鱼缸共用玻璃多少平方分米？（玻璃的厚度忽略不计）

说切入点：题目要做一个鱼缸，鱼缸只有5 个面，所以可以先确定底面再配侧面，也可以先确定侧面再配底面。

说方法：解决这道题目我们可以采用分析法、假设法、观察法，或者动手操作的方法。

说思路：我们先确定底面再配侧面，可以配对挑出5 块，或排除一块。假设选择D作为底面，那么就需要两块长6dm，宽一样的玻璃，有E 和F，那么剩下就需要两块长5dm、宽3dm的玻璃，没有就排除D，选择剩下的5 块，把5 块玻璃的面积加起来就是鱼缸的表面积了。

（三）说解题步骤

有了解题思路，接下来就要通过具体解题步骤将过程清晰的呈现出来，这一过程包括答题规范和结果检验。

1.答题规范

小学数学答题规范包括作图规范和求解规范。结合《长方体和正方体》的内容，说作图规范包括用尺规作图，用铅笔作图，添加的点要有相应的标识，看得到的线用实线，看不见的用虚线等。说求解规范包括分步求解用序号标注，从上到下、从左到右书写，求周长、面积、体积要写明公式等。

2.说检验过程

说检验过程不仅包括计算结果的检验，更重要的是检验结果的合理性。

“说解题步骤”案例分析：

题目：一个长方体高增加5 厘米后变成一个正方体，此时表面积增加了1.4 平方分米，原来长方体的体积是多少？

说解题步骤和答题规范：第一步是单位换算；第二步求原来长方体的底面周长，增加的表面积= 高为5 厘米的长方体的侧面积，我们可以根据S侧=C底h，列式140÷5=28（厘米）求出了底面周长；第三步求出底面边长，能变成正方体说明原来长方体的底面是一个正方形，根据C正=4a，列式28÷4=7（厘米）求出底面边长；第四步求原来长方体的体积，根据V正=a3，列式7×7×（7- 5）=98（立方厘米），由于增加5 厘米后是棱长为7 厘米的正方体，所以原来长方体的高是2 厘米，求体积时应先求出高。

说检验过程：原来长方体的长宽高是7cm、7cm、2cm，表面积是154cm2，增加后成为棱长7cm的正方体，正方体的表面积为294cm2，表面积正好增加了140cm2，符合题意。

（四）说回顾反思

如何避免原题重做出错，做到解一题而通百题呢？一个简单有效的办法就是解完题目后，静下心来回顾与反思。

1.说深层思考

对题目进行深层思考，我们解完题后可以尝试站在出题人的角度想想这个题目是怎么编出来的，在题目中设置了什么样的“陷阱”是我们在解题中要注意避免的，题目中最巧妙的地方是什么等。

2.说一题多解

很多数学题往往有多种解法，当我们找出一种方法解答完成后不妨多想想还有其他方法吗？把多种方法都想一想、说一说，不仅有助于提高我们思维的灵活性，更能发现解题的乐趣。

3.说方法总结

学生说题不应该只是“解一题说一题”，要“就一道题论一类题”，解完这道题要思考今后遇到类似的问题怎么解决，说题时要说清题目所涉及的方法和规律。

4.说变式拓展

题目变式可以从横向拓展和纵向延伸两个维度展开，变式拓展是深化知识理解的有效途径，同时对学生的综合能力要求也是比较高的，可以从比较简单的变式开始，比如变换已知条件和问题。

“说回顾反思”案例分析：

题目：一个长方体水槽，长10dm，宽8dm，高6dm，水深3dm。将一个棱长4dm等正方体铁块放进水槽后，这时水槽内的水深是多少？

说深层思考：1.水会不会溢出？答题时应注意将结果和水槽高度进行比较。2.正方体铁块会不会被完全浸没？浸没或者不浸没对于等量关系“上升的水的体积=浸没在水中的物体的体积”是否有影响？今后遇到类似问题可否统一使用这一等量关系展开思考？

说一题多解：

方法一：先判断是否完全浸没，完全浸没时上升的水的体积为80dm3，铁块的体积为64dm3，所以没有完全浸没，那么根据水的体积不变，底面积变小，可以列式10×8×3÷（10×8- 4×4）求出水的高度为3.75 分米。

方法二：根据等量关系“容器底面积和水面高度差的乘积= 浸没在水中的物体的体积”，假设水的高度为H分米，可以列出方程“10×8×（H- 3）=4×4×H”，求出“H=3.75”。

说方法总结：本题运用了分析法或者方程法，根据水的体积不变开始思考，在题目情境的变化中以不变应万变。

说变式拓展：本题是浸没水中，那么如果反过来是提出水面呢？顺着这个思路，题目可以拓展为“一个长方体水槽，长10dm，宽8dm，水槽里立着一个棱长4dm的正方体铁块，这时容器里的水深为3dm，现把铁块轻轻向上提起10cm，那么露出水面的铁块上被水浸湿的部分长多少厘米？”这一变式拓展题仍然可以根据原来的等量关系直接列方程求解。

三、结语

本文从说审题分析、说解题思路、说解题步骤、说回顾反思四个角度阐述小学生数学说题的结构框架，并提供了相应的说题分析案例。这四个角度彼此联系，环环相扣，全面锻炼学生的综合能力。学生说题活动以学生为主体，以教师为主导。通过学生说题，不仅可以培养学生的反思能力和实际解决问题的能力，促使学生在说题反思的过程中，不断优化知识结构和方法体系，提升思维品质，而且有利于教师获得教学反馈，从而有针对性的地组织教学，促进教育教学质量不断提升。