耗散诱导的非厄米边缘爆发重现*
任翠翠 尹相国
(山西大学理论物理研究所,量子光学与光量子器件国家重点实验室,极端光学协同创新中心,太原 030006)
开放量子系统在一定程度上可由等效的非厄米哈密顿量来描述,因此探究非厄米系统的耗散作用有许多重要的现实意义.本文研究了开边界条件下一维非厄米系统中与耗散强度相关的动力学规律,发现耗散可诱导边缘爆发重新出现.粒子在开边界条件下的一维非厄米耗散晶格系统中进行含时演化后,系统存在边缘爆发即在边缘处有较大的粒子损失概率,而增大胞内跃迁强度后边缘爆发消失,研究发现若增大或者减小耗散强度,边缘爆发会重新出现.这种重现的与原先的边缘爆发有所不同,主要表现为粒子的损失概率分布由边缘分布趋向于体分布,这是由于两种情况下粒子运动方向的概率不同;更深层的原因与非厄米系统远离宇称-时间对称破缺点有关.另外还研究了杂质势垒对非厄米动力学中粒子损失概率分布的影响,结果表明在无耗散的A 格点上放置很小的势垒就能明显地阻碍粒子运动,并且当势垒增大到一定高度后,其对粒子运动的影响趋于不变.
1 引言
在量子力学中,一般采用厄米哈密顿量描述理想情况下的封闭量子系统,但在现实中物理系统与环境密切相关,而耦合于环境的开放量子系统在一定程度上可由等效的非厄米哈密顿量来描述,故在现实生活中非厄米物理广泛应用于各领域,例如有损失和增益的光学系统[1-3]、开放量子系统[4-6]和具有有限寿命的准粒子等[7-9],探究非厄米物理具有重要意义.在非厄米物理的研究中,发现了许多区别于厄米体系的独特性质,其中一个重要的物理现象是非厄米趋肤效应(non-Hermitian skin effect,NHSE),即在开边界条件下本征态一般是以指数衰减的形式局域在系统的边界附近.非厄米趋肤效应带来了大量的讨论和探究[10-14],发展出了非厄米相关理论: 系统中的体-边对应被破坏,需要在非布洛赫能带理论下定义广义布里渊区,在此基础上计算新的拓扑不变量非布洛赫缠绕数以恢复体-边对应[10,15].其中,体-边对应是指体系在周期性边界条件下的拓扑不变量和开边界条件下边缘态的个数之间存在着对应关系.如今,在各领域中非厄米物理的研究依然很活跃,实验与理论方面的探索展现出了非厄米体系许多新奇的物理现象和规律[16-21].
对于存在耗散的非厄米开放量子系统而言,探究体系的动力学有助于我们理解现实情况下量子系统变化的过程[22-24].采用量子行走这一种普遍的量子模拟方案可研究具有耗散的一维非厄米体系的动力学问题[25],并且量子行走这一方案已经在许多的物理环境实验中[26-32]实现.最近,王利课题组[33]在有耗散的非厄米系统的动力学研究中发现了边缘爆发现象即在边缘处有明显的粒子损失概率峰,并对此进行了深入的探究.Xue 等[34]研究表明边缘爆发产生的原因是两个非厄米特性的共同作用: 非厄米趋肤效应与周期性边界条件下能谱虚带隙闭合,并提出了发生边缘爆发时体上的损失概率和边缘处损失概率之间存在一定规律的观点.众所周知,耦合于环境的耗散强度与非厄米量子系统动力学性质的关系十分密切,边缘爆发也将受到其影响,因此研究耗散如何影响粒子损失具有重要的现实意义.
本文讨论了耗散强度对一维非厄米格点系统动力学性质的影响,发现了一些有趣的现象和规律: 在边缘处本无粒子损失的系统中增大或者减小耗散强度可重新诱导出较明显的损失概率,将这一现象称为耗散诱导的非厄米边缘爆发重现.具体来说,在有耗散的一维非厄米格点系统中放入随时间演化的粒子(量子行走者),其以一定的概率从体系中损失掉,通过数值计算得到粒子的损失概率分布,可以发现粒子在边缘处有较大的概率损失掉也就是存在边缘爆发现象;当增大胞内跃迁强度边缘爆发消失[33].在无边缘爆发的体系中增大耗散强度,预想为在耗散增强后初始位置附近的损失概率会变得更大,且不会影响到边缘处无粒子损失的这一特征,但结果却是粒子在边缘处相较于初始位置出现了明显的损失,并发现在较弱的耗散作用下有类似的重现现象.同时,研究发现重现的与原先的边缘爆发在粒子损失概率分布上有所不同.原先边缘处的损失概率是一个孤立的峰,而在较强或较弱的耗散作用下,粒子损失概率从边缘处向体内逐渐扩展且初始位置右侧也变得有损失.研究得到造成此现象的原因是两种情况下粒子做量子力学演化时运动方向的概率不同,进一步分析表明其运动方向的概率产生差异的深层原因与体系是否靠近宇称-时间(parity-time,PT)[22,35]对称破缺点有关.最后分析了添加杂质势垒对粒子损失概率分布的影响.
第2 节介绍了纯耗散的一维非厄米格点模型及理论方法,3.1 节展示了边缘爆发重现并对其特征进行了描述;3.2 节确认了耗散作用可诱导边缘爆发重现;3.3 节分析了两种边缘爆发中粒子损失概率由边缘分布趋向于体分布的深层原因;3.4 节考察了势垒对粒子损失的影响,最后在第4 节中进行总结.
2 模型与方法
考虑一维非厄米耗散晶格模型,如图1 所示,哈密顿量写作:

图1 一维非厄米耗散晶格模型,每个原胞由A 和B 两个子格点组成Fig.1.One-dimensional non-Hermitian dissipative lattice model,and each unit cell consists of two sublattices A and B.
由薛定谔方程 i ℏ(d/dt)|ψ(t)〉=H|ψ(t)〉 得到量子行走者的运动方程:
右侧求和中的每一项对应了各原胞的B格点在不同时间下的损失速率.当演化时间无穷大后粒子从此系统中完全损失到外界环境.若将原胞上的损失速率 2γ|(t)|2对所有时间进行积分可计算得到各原胞上的损失概率:
3 一维非厄米耗散系统中的动力学
3.1 耗散作用诱导边缘爆发重新出现
在具体计算中,假设粒子在初始时刻位于第x0个原胞的A格点,即,取总原胞数L=50 及初始位置x0=25 .粒子按照运动方程(2)进行演化,可得到每个原胞上波函数模方的时间演化过程,如图2第2 列;由于粒子在B格点上损失,故也关注B格点上波函数模方的时间演化过程 |(t)|2,如图2第3 列;第4 列放大了第3 列中粒子在边缘处演化的细节;并由(3)式得到粒子损失概率分布Px,如图2 第1 列.
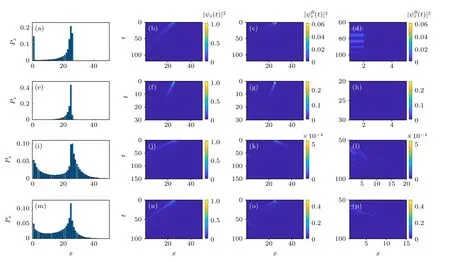
图2 不同耗散强度下的粒子损失概率分布图和波函数模方的时间演化过程 (a),(e),(i),(m) 粒子损失概率分布图;其余为波函数模方的时间演化过程.(a)—(d) v=0.3 ;(e)—(p) v=0.7 ;(a)—(h) γ=0.5 ;(i)—(l) γ=30 ;(m)—(p) γ=0.05 ;共同参数 r=0.5,L=50,x0=25Fig.2.Probability distribution diagram of particle loss and the time evolution process of wave function module square under different dissipation: (a),(e),(i),(m) Distribution of particle loss probability;the rest of the figure is the time evolution process of the norm of the wave function.(a)—(d) v=0.3 ;(e)—(p) v=0.7 ;(a)—(h) γ=0.5 ;(i)—(l) γ=30 ;(m)—(p) γ=0.05 .Common parameters: r=0.5,L=50,x0=25 .
当v≤r时,边缘处有较大的损失概率即有边缘爆发现象如图2(a)所示;而增大胞内跃迁强度使得v>r时在边缘处无明显的粒子损失概率,边缘爆发消失如图2(e)所示,这些现象已被文献[33,34]证实过.本文研究表明耗散强度γ极大地影响了非厄米耗散系统的动力学,且耗散可诱导非厄米边缘爆发重现.当在边缘爆发消失的图2(e)的基础上增大耗散强度,使γ由0.5 变为30,发现在边缘处重新出现了较明显的损失概率(相较于系统整体的损失概率分布),如图2(i)所示.
注意到改变耗散强度诱导的边缘爆发与原先的边缘爆发有所不同,具体表现在粒子损失概率分布图上.原先存在边缘爆发的系统在损失概率分布图中表现为边缘处是独立的一支峰,如图2(a)所示,而耗散诱导的边缘爆发系统则是由边缘处缓慢扩展于体内如图2(i)所示,并且在初始位置的左右两侧都有分布.造成损失概率分布有差异的原因是粒子运动方向的概率不同,可直观地从波函数模方的时间演化过程(图2)中看出: 图2(j)—(l)表明在强耗散作用γ=30 下,粒子在初始时刻有沿趋肤效应朝左和相反于趋肤效应朝右演化的概率,并且其中沿着趋肤效应方向演化的粒子运动到边缘后做反弹运动(开边界的本征态分布可表明趋肤效应方向,此非厄米系统趋肤效应的方向类似于图3(c)中插图所示向左).在强耗散作用γ=30 下的边缘爆发中,粒子以上述的运动方向演化,形成图2(i)的粒子损失概率分布.而在原先的边缘爆发中,例如图2(b),(d)粒子沿着趋肤效应方向运动至边缘且“困”于边缘附近继而损失尽,形成图2(a)的概率损失分布.造成边缘爆发损失概率分布有差异的深层原因将于3.3 节中探讨.

图3 (a)不同初始位置时边缘峰与最小值的相对高度比 Pedge/Pmin ;(b)不同初始位置时边缘峰与整个体系中最大值的相对高度比 Pedge/Pmax ;(c)周期性边界条件下能量虚部最大值的模,插图为 γ=30 时开边界条件下本征态的模方|ψx|2 的分布;(d)周期性边界条件下的能量虚部最大值(γ 轴取对数),红线为 v=r 表示胞内胞外跃迁强度相等,蓝线是PT 对称性的分界线|γ|=2v .(a)—(c)为双对数坐标,v=0.7,L=200 ;(d)横坐标取 l n γ,标记4 个点,γ=0.05 蓝色三角形对应图2(m);γ=0.5洋红色十字对应图2(e),γ=30 红色五角星对应图2(i),以及将图(d)中 v=0.3,γ=0.5 标记为黑点对应图2(a).共同参数r=0.5Fig.3.(a) Relative height ratio of edge peak to minimum Pedge/Pmin at different initial positions;(b) relative height ratio of edge peak to maximum in the system Pedge/Pmax ;(c) the modulus of the maximum imaginary part of energy under periodic boundary conditions,the inset shows the distribution of eigenstates|ψx|2 under open boundary with γ=30 ;(d) maximum energy imaginary part under periodic boundary(axis γ is logarithm),the red line indicates that the intracell and intercell hopping is equal v=r,and the blue line is the boundary of PT symmetry|γ|=2v .(a)—(c) With double logarithmic coordinates,v=0.7,L=200,(d) abscissa l n γ .Mark four points: γ=0.05 blue triangle corresponding to Fig.2(m);γ=0.5 magenta cross corresponding to Fig.2(e);γ=30 the red pentagram star corresponding to Fig.2(i);v=0.3,γ=0.5 in panel (d) is marked as a black dot corresponding to Fig.2(a).Common parameters: r=0.5 .
当v>r时,耗散强度较小如γ=0.05 的系统也存在边缘爆发现象,其粒子损失概率分布和波函数时间演化都类似于较大耗散γ=30 时的情况,如图2(i)—(p)所示.但是γ取较大时B格点上波函数模方 |(t)|2的数量级远小于γ取较小时的量级,如图2(k),(l)与(o),(p)中颜色条的值所示.
3.2 确认耗散作用可诱导边缘爆发重现
本节通过数值计算确定了改变耗散强度可诱导边缘爆发重现.作出边缘峰与最小值的相对高度比Pedge/Pmin,如图3(a)所示,其中Pmin≡min{P1,P2,···,Px0}指从初始位置到左边缘之间最小的损失概率.若Pedge/Pmin远大于1 则表示边缘处有明显的损失概率;若Pedge/Pmin比值接近1 则表示边缘处无较明显的损失概率.图3(a)中x0=100和x0=150 的计算结果表明当v>r时,耗散强度在γ=0.5 附近的Pedge/Pmin接近1,无边缘爆发;而左右两侧耗散强度γ=0.05 和γ=30 附近的比值较大,有边缘爆发.图3(b)中Pedge/Pmax为边缘处损失概率与整个系统损失概率分布中最大值的比值,若接近1 说明有边缘爆发;若远小于1 (接近于0)时相反.图3(b)表明当γ=0.5 时系统无边缘爆发,而当γ=0.05 和γ=30 时有边缘爆发.
图3(a)和图3(b)在3 个耗散强度参数标记点上的分析结果对应图2(e),(i),(m)中L=50 的边缘爆发情况,区别为图3 取L=200 .若用长链系统x0=100 和x0=150 也可观察到与图2(e),(i),(m)相同的边缘爆发情况,但此时波函数所展示的粒子运动的效果不如短链清晰,故选取L=50 短链系统作图2.而短链系统尺寸的局限性会影响Pedge/Pmin的结果,影响边缘爆发的判断,故用图3(a)中x0=100 和x0=150 的长链系统分析边缘爆发.L=50,x0=25 与L=200,x0=25 两个系统中的Pedge/Pmin一致,也可将后者的计算结果称为短链系统的值,将x0=100 与x0=150 称为长链系统.图3(a)展示了短链系统的与长链系统中Pedge/Pmin的差别.
以3 个标记为例说明短链系统的尺寸局限对Pedge/Pmin的影响: 文献[34]提到有限链边缘处损失概率与无穷长链在远处的积累有关,γ=0.5 (洋红色十字处参数)时短链系统的边缘处仍有较小的损失概率(放大多倍后可观察到),这使短链的Pedge/Pmin增大.而在γ=0.05 (蓝色三角形参数)和γ=30 (红色五角星参数) 时的短链系统中,由于粒子运动到左边缘后反弹,使得Pmin经粒子反弹的积累后变大,进而Pedge/Pmin减小,如图3(a)所示.短链系统的尺寸局限使得短链中Pedge/Pmin的值在γ=0.5,0.05,30的结果大致相同,无法相互区别并判断边缘爆发现象.因此依据图3(a)中x0=100 和x0=150长链系统的Pedge/Pmin计算结果,同时结合图3(b)中Pedge/Pmax进行分析(其在长和短链系统下都有同样的趋势),更好地解释了当v>r时γ取较大和较小时有边缘爆发的重现.
Xue 等[34]的研究提到出现边缘爆发现象需要同时满足两个非厄米的独特性质,即周期性边界下能量虚部带隙闭合与存在非厄米趋肤效应.图3(c)的插图表明在γ=30 的强耗散作用下存在趋肤效应,(在γ=0.05 的弱耗散作用下同样存在趋肤效应),这满足了边缘爆发的其中一个条件(γ=0 或v=0时无趋肤效应,无边缘爆发).接着探究周期性边界条件下能量虚部与耗散作用的关系.由布洛赫哈密顿量:
计算得到周期性边界条件下的能量本征值:
其中k∈[0,2π],σx和σz为泡利矩阵,由于是纯耗散体系,能量虚部 I m(Ek)≤0,上述带隙指能量虚部最大值与零的间距.周期性边界条件下能量在复平面上形成了闭合的曲线这与开边界存在趋肤效应相等价[36,37].由(5)式作出周期性边界条件下能量虚部最大值的模随耗散强度γ的变化情况,如图3(c)所示.图3(c)表明随着耗散增强,周期性边界下能量虚部最大值的模先增大后减小,在γ较强或较弱时能量虚部最大值接近零,满足了出现边缘爆发的另一条件.周期性边界条件的能谱虚部最大值不为零,对应的粒子耗散率较大,即粒子很快耗散到环境中去,而不会到达边缘,因而没有边缘爆发;而当能谱虚部最大值接近为零时,粒子耗散率较小,容易到达边界处,形成边缘爆发.
图3(a)—(c)确定了边缘爆发重现,现将参数范围扩大为图3(d)所示,即可与图2 相对应(图3(d)横坐标取 l nγ,所以v和γ从接近零的数开始).存在边缘爆发的图2(a)增大胞内跃迁强度后边缘爆发消失变为图2(e),再增大或减小耗散强度后变为有边缘爆发的图2(i)或图2(m).将上述过程对应于图3(d)中:v由小到大,例如从黑色点到洋红色十字,颜色由黄色进入绿色区域,代表能量虚部最大值远离零,对应边缘爆发消失.接着增大或减小γ,向右或左移动重新进入右侧红色五角星处或到达左侧蓝色三角形处,代表能量虚部最大值接近零,对应边缘爆发重现.因此从图3 可得出结论:v <r存在边缘爆发(其中v≠0 且γ≠0),且较小和较大的耗散强度可以在v>r的体系中重新诱导出边缘爆发.
注意到在v>r区间γ从零增大到非常小参数值时边缘爆发为从无到有,是连续变化的过程.由于本征能量和其对γ的一阶以及高阶导数随着γ变化都是连续(图5(a)的能量虚部),不存在发散行为,故系统从γ=0 到非常小值的转变是连续的,不存在量子相变.当γ由零到非常小的值时,对应系统由无损失到损失概率在空间中大体呈现均匀分布(γ非常小时只有在初始位置有一个小峰,而边缘处没有出现峰值).当γ从非常小变为较小时损失概率分布在空间上不再均匀,在边缘处慢慢出现了峰值,同时初始位置的峰值越发明显,如图2(m)γ=0.05所示.
3.3 两种边缘爆发中粒子损失概率分布有差异的深层原因
在 3.1 节提到的现象即在耗散诱导边缘爆发的系统中,粒子损失概率为边缘向体内扩展分布产生的深层原因.发现粒子运动方向的概率不同与体系是否远离某特定转变点有关.图4 为初始位置右侧第3 到6 个原胞处(x=x0+3,x0+4,x0+5,x0+6)的粒子损失概率,在同一参数下从初始位置越向右粒子损失概率越小.同时分析发现在耗散强度γ取某值时初始位置右侧的损失概率为零,即粒子无向右运动的概率,而远离此γ值时,初始位置右侧的损失概率增大,该点在后面中被证明此转变点为PT 对称破缺点,具体为|γ|=2v(这里考虑v >0).故当在转变点附近,粒子向右运动概率较小,且因存在趋肤效应粒子朝左运动到边缘后“困”于边缘处,并随着演化完全损失到体系外形成单独的损失峰,如图2(a)所示;而远离转变点时向右的运动概率较大,初始位置向左右两个方向运动,且向左运动的粒子到达边缘处反弹向右运动,形成图2(i),(m)中粒子损失概率分布图所呈现的由边缘向体内扩展且初始位置右侧也有分布的特点.因此耗散作用重新诱导出的边缘爆发与原先的边缘爆发在粒子损失概率分布图上不同的深层原因是:体系远离了PT 对称破缺点.
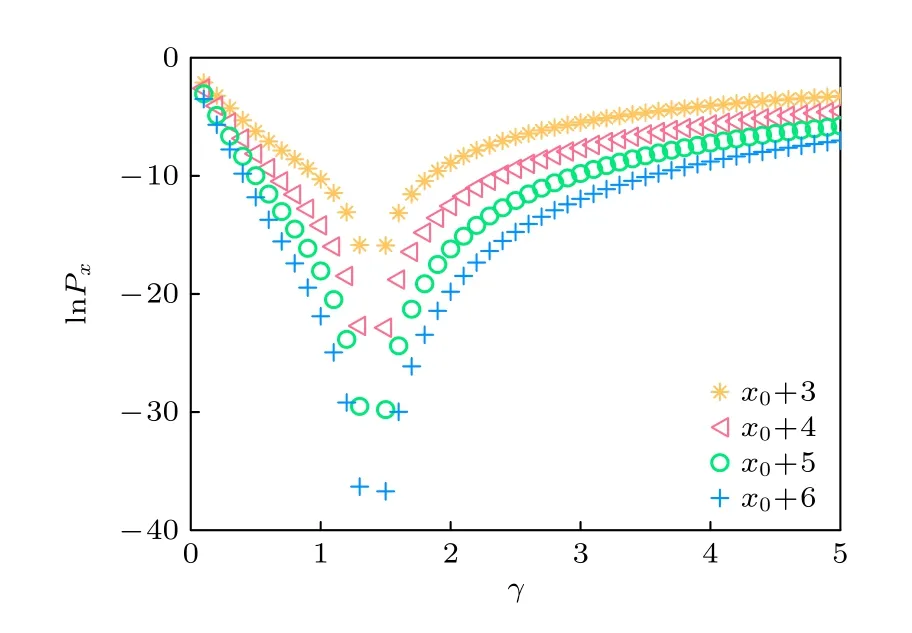
图4 初始位置右侧原胞的损失概率随耗散强度的变化.右侧原胞位置x 分别取 x0+3,x0+4,x0 +5,x0 +6,其中 v=0.7,L=50,x0=25,r=0.5Fig.4.Loss probability of the right cell at the initial position varies with the dissipation intensity.Right cell position x is taken as x0+3,x0+4,x0 +5,x0 +6 respectively with v=0.7,L=50,x0=25,r=0.5 .
在存在边缘爆发v≤r的系统中,初始位置右侧原胞的损失概率随耗散强度的变化类似于图4,其在较大和较小的耗散强度区间上的粒子损失概率也类似于v>r时的分布,为向体内扩展型分布(除无耗散γ=0 参数,因为无边缘爆发).综上所述,先在3.2 节中由产生边缘爆发的两个非厄米特性条件判断得到存在边缘爆发的区间,得到图3(d),然后在3.3 节中进一步由体系靠近或远离PT 对称破缺点解释边缘爆发系统的粒子损失概率为边缘分布或向体内扩展分布.
下面是关于上述转变点|γ|=2v为体系PT 对称点的讨论.其中,PT 对称破缺点的含义阐述如下: 1998 年,Bender 和Boettche[38]发现在非厄米系统中,哈密顿量在空间和时间反演的共同作用下不发生改变的系统具有PT 对称性,在一定参数区间内开边界能谱为纯实数,对应系统处于PT 对称相,改变参数后能谱为一对共轭的复数,对应系统处于PT 破缺相,两个相的临界处即为PT 对称破缺点[22,39].本文的一维非厄米耗散系统在Lee 模型[22]的基础上整体平移 -iγ/2,但两种系统的转变点位置不变,故将此处也称为PT 对称破缺点.非厄米物理中关于PT对称的研究在不断地发展,可以参考文献[39-45]了解最近的动态.图5(a)表明开边界能谱的虚部在|γ|<2v的区间内能量虚部为-γ/2处于PT 对称相中,此结果与Lee[22]研究提到的PT 对称性相同.根据非布洛赫能带理论可知本文模型的广义布里渊区是半径的圆形,作出半径R随γ的变化,如图5(b)所示.发现在γ>0 时R< 1 而在γ<0 时R> 1,对应趋肤效应是向左或向右[37,46],当γ=±2v时半径R为零或无穷大.进一步可由非布洛赫能带理论得到开边界条件下的能量,利用广义布里渊区是半径为R的圆这一特征,从理论上计算得到PT 对称性的临界位置|γ|=2v.
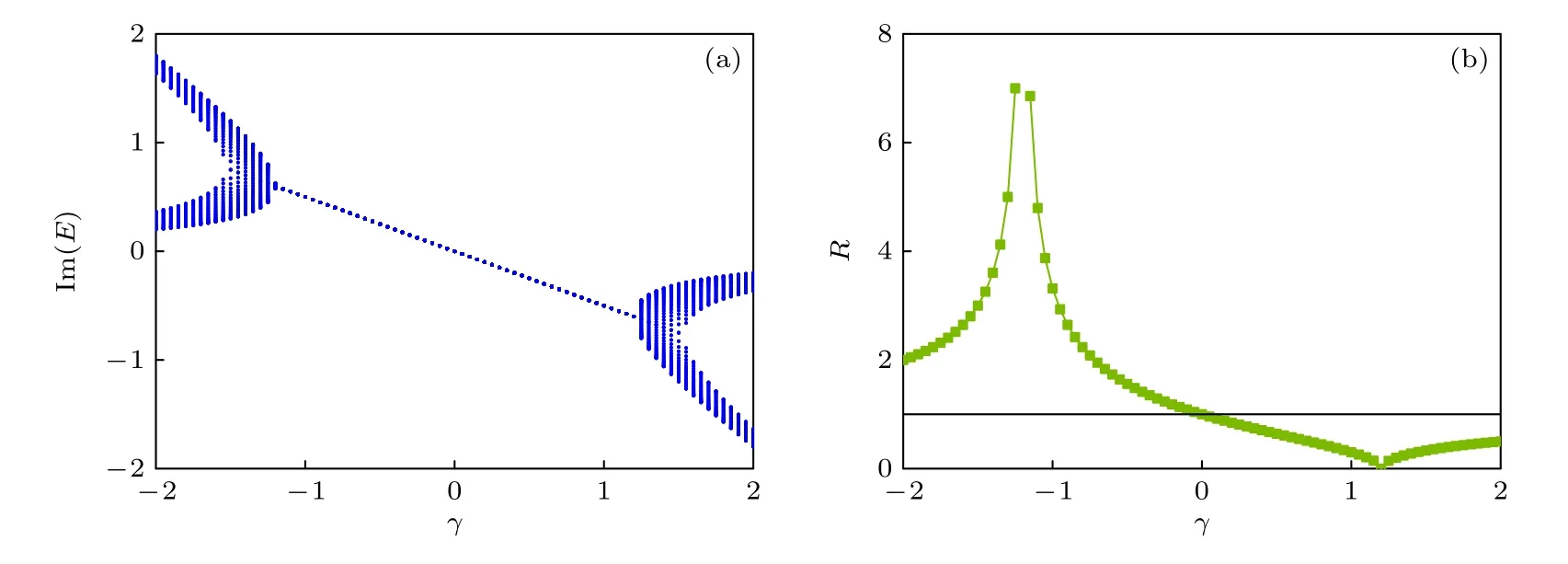
图5 (a)开边界条件下能量本征值虚部随耗散强度的变化,L=50 ;(b)广义布里渊区的半径 R,黑色直线为 R=1 代表布里渊区半径.共同参数 r=0.5,v=0.6Fig.5.(a) Change of imaginary part of energy eigenvalue with dissipation intensity under open boundary condition with L=50 ;(b) R the radius of the generalized Brillouin zone,the black line represents the radius of Brillouin zone with R=1 .Common parameters: r=0.5,v=0.6 .
非互易Su-Schrieffer-Heeger (SSH)模型[10]哈密顿量为
在数学上可等价为Lee 模型.在此模型中胞内跃迁有两个方向,强度分别为 (v+γ/2) 和 (v-γ/2),胞间跃迁强度为r.当γ=±2v时仅有一侧的胞内跃迁强度不为零,粒子沿某一方向运动;γ在此参数附近时同样朝一个方向的运动概率大,对应本文模型中损失概率的单侧分布,如图2(a),(e)所示.当γ取值很小或很大时胞内两个方向的跃迁强度的大小接近相等,粒子向两侧运动对应本文中损失概率的双侧分布,如图2(i),(m)所示.
3.4 势垒对非厄米动力学的影响
在此系统中添加杂质势垒,探究势垒对损失概率产生的影响.将杂质势垒设置于第10 个原胞,相应的哈密顿量写作:
其中VA,B分别表示在A或B格点上的势垒强度.
首先,仅在A格点处放置势垒,如图6(a)所示,势垒增大的过程中边缘上粒子损失概率P1迅速降低后缓慢变化;含势垒的杂质原胞及其右侧相邻原胞处的损失概率P10与P11的值从零迅速升高到一定高度后缓慢变化,最终P1,P10和P11形成3 个平台.取图6(a)中势垒最大值V=0.15 作出图6(d)粒子损失概率分布,其中3 个损失峰与图6(a)中3 个平台相对应,并发现仅有少部分粒子通过杂质原胞到达边缘,表明A格点处设置势垒会明显地影响粒子运动.其次,在B格点上放置势垒,见图6(b).图6(b)表明P1值较大且不随耗散强度明显变化,P10逐渐接近于零,P11有略微增大.图6(e)中B格点上势垒V=0.15,表明B格点上的势垒不会明显地影响粒子损失概率分布,粒子主要还是在A格点通道运动.最后,在第10 个原胞的A和B格点处同时加入等大的势垒,如图6(c)所示,随着势垒升高,P1减小,P10先增大后减小;P11逐渐增大随后缓慢变化形成一个平台.在势垒为0.15 时杂质原胞的右侧形成一个损失峰P11,见图6(f),此势垒相当于将边界移到第10 个原胞处,对应图6(c)的平台.结果表明,在不存在耗散的A格点上加很小的势垒就会明显阻碍粒子运动,且当势垒增大到一定高度后其对粒子运动的影响趋于不变.

图6 在第10 个原胞不同格点处放置势垒的粒子损失情况 (a)—(c)在边缘处、杂质原胞处以及杂质原胞相邻原胞上的损失概率 P1,P10 和 P11,图(b)中插图为 P10 和 P11 随势垒变化的细节;(d)—(f)势垒强度 V=0.15 时3 种势垒设置下的粒子损失概率分布.(a) VA=V ,VB=0 ;(b) VA=0,VB=V ;(c) VA=VB=V ;(d) VA=0.15 ,VB=0 ;(e) VA=0,VB=0.15 ;(f) VA=VB=0.15 .共同 参数 v=0.3,r=0.5,L=50,x0=40,γ=0.5Fig.6.Particle loss of the barrier placed at different lattice points of the tenth cell: (a)—(c) Loss probability at the edge,the impurity cell and the adjacent cell of the impurity cell P1,P10 and P11,the inset in panel (b) is the detail of P10 and P11 changing with the barrier;(d)—(f) the probability distribution of particle loss under the three barrier settings with the barrier V=0.15 .(a) VA=V,VB=0 ;(b) VA=0,VB=V ;(c) VA=VB=V ;(d) VA=0.15 ,VB=0 ;(e) VA=0,VB=0.15 ;(f) VA=VB=0.15 .Common parameters v=0.3,r=0.5,L=50,x0=40,γ=0.5 .
4 结论
本文在一维非厄米有耗散的系统中改变耗散强度和势垒强度,通过数值计算考察了粒子损失概率分布和波函数的时间演化过程,研究了其动力学性质,结果展示出了丰富而有趣的现象.研究发现耗散作用可以诱导边缘爆发重现,与原先的边缘爆发粒子损失概率分布为边缘分布不同,重现的边缘爆发粒子损失为体分布,原因是粒子运动方向的概率不同,深层原因与非厄米体系是否远离PT 对称性破缺点有关.在重新诱导出的边缘爆发下粒子由初始位置向左右两方向运动,左侧到达边界后反弹运动,形成了边缘处有较明显的损失概率,并逐渐向体区域递减且初始位置右侧也存在损失概率的分布情况.而在原先的边缘爆发下,粒子仅向左运动概率较大,“困”在边缘处至完全耗散,形成在边缘处有一支独立损失峰的分布情况.当v>r时体系在PT 对称破缺点附近时粒子几乎仅沿着趋肤效应方向运动;远离PT 对称破缺点时粒子有更大的朝与趋肤效应相反方向运动的相对概率,这是两种边缘爆发差异的深层原因.最后,本文关于势垒的研究表明在无耗散的A格点上放置很小的势垒就会对此一维非厄米耗散系统的动力学产生明显的影响,当势垒增大到一定高度后,其对粒子运动的影响趋于不变,而耗散B格点处的势垒对动力学影响较小.目前非厄米的拓扑和动力学方向的研究仍然很活跃,本次研究仅关注了一部分,玻色子费米子多体的动力学等问题会展示更多有趣的现象.
感谢山西大学王利和陈立提供有益的讨论,作者对非厄米的物理现象和理论有了更深刻的理解.

