问题引领，深化思维

郭苗

摘要：思维品质是数学的灵魂，数学是思维的“体操”，可以培养学生的思维能力。网状课堂下的教学活动是教师与学生、教材与学生、学生与学生之间的思维碰撞，对学生思维品质的培养要落实到数学课堂教学中。

思维品质是教师根据教学内容有目的有计划地在有效的课堂活动中培养出来的。问题是思维的起点，是探究的动力。课堂需要有充分思考价值、适宜探究空间、无限对话可能的数学问题，通过教师有效的课堂提问策略，提升学生的数学思维能力。

关键词：小学数学  思维品质  策略

一、创设问题情境，激发思维积极性

结合学生已有的经验、认知基础、思维方式，创设真实、有效的问题情境，激发学生通过自己努力解决数学问题的积极性，让学生能在教师所创设的问题情境中快速展开思考，寻找解决数学问题的方法。在问题探究中，驱动了学生的学习兴趣，驱动了学生感受数学与生活的联系，驱动了学生探求知识的欲望，从而实现数学思维能力的提升。

例如，教学“三角形面积的计算”一课时，就可以通过创设有趣的问题情境来引入新课，激发学生探索新知的兴趣，在新课开始前，可以让学生准备一张形状是三角形的彩纸，问学生：“这张彩纸的形状是什么？”“你会算出这个三角形彩纸的面积吗？”这样就引出了本节课所要探索的重点内容——“三角形面积的计算”。

在提出这些问题之后，学生可能会感到无从下手，不知道该如何计算三角形的面积，这时再给予一定的提示，比如说： “怎样把三角形转化成我们已经学过的图形？”让学生利用手中的彩纸进行拼接，通过操作把三角形拼成平行四边形，在学生一番动手操作之后，就能很容易发现两个三角形拼接在一起就是一个完整的平行四边形，平行四边形的底就是三角形的底，平行四边形的高就是三角形的高，学生就可以很容易推导出三角形的面积计算公式。这样，学生就能产生自主探究问题答案的兴趣，在問题解决的过程中，学生的数学思维能力也能得到很好的提升。

二、进行问题探究，拓宽思维宽度

在问题引领教学中，教师要注意给学生留下自主思考的空间，让学生在探究与猜测中自然生成对核心概念的理解，这也是为了拓宽学生思维活动的宽度。开放而延续的问题引领，激起一个个思维旋涡，引导学生经历一个从头到尾思考问题过程，将思维逐渐引向问题的本质。

（一）明暗交织

明暗交织就是将题目信息“露一半遮一半”，适当留白让学生探究的兴趣更浓，获得的体验更深。这就需要让学生挖掘隐性信息，沟通显性信息与隐性信息之间的联系。“曲径通幽”往往比“一览无余”更有味道。

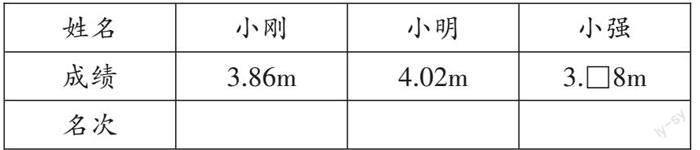
例如，“小数大小的比较”的学习材料：校运动会上的一张跳远成绩记录单，很遗憾，不完整，根据这些信息，你能确定什么？

生：小明是第一名。

师：小强的信息记录不完整，你是怎么比较出来的。

小结：比较小数的整数部分比较出第一名。

师：谁第二名呢？

生：还不能确定，因为不知道3.□8m中的□是多少？

师：如果小强是第二名，□是多少呢？

如果小刚是第二名，□又是多少呢？

明暗交织的信息，“逼”着学生去思考，提升了例题的思维训练价值，使探究活动变得更加自主、高效。

（二）正反结合

只讲正确的东西，忽略让学生去证实或证伪自己的假设，那么对概念的理解就不够深刻和全面。学生认识概念需要经历“正例→变式→反例→正例”的过程，从变式中剥离概念的非本质属性，再从反面证明衬托出概念的本质。再往前走一小步，经历反例→正例的过程，更能凸显概念的本质。

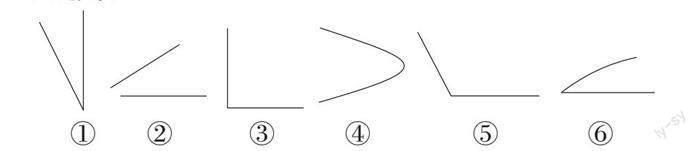
例如，“角的初步认识”：判断下面哪些是角，哪些不是角。

第一步判断哪些是角，哪些不是角。第二步变式辨析，旋转图③，边旋转边问：现在还是角吗？旋转结束后让学生思考：为什么一直都是角？通过变式辨析剥离角的非本质属性——方向，使学生明白只要是角的特征没有变，方向虽然变了，也还是角。第三步，经历反例→正例的过程，就是将图②和图⑥渐变成一个角。学生在经历反例→正例的过程中逐步感悟出角的本质特征。

（三）动静结合

在动态与静态下研究变与不变的规律，现象的反差和矛盾使学生产生认识和情感上的“冲突”，激发学生探究的欲望。不断的比较和反思帮助学生学会抓住解决问题的关键，学生从中会掌握一种思考和解决问题方法，整个过程中学生获得的发现是真实的、全面的、深刻的，而发现的过程具有一定的挑战性，起点不同的学生都会获得发展。

例如，“平行四边形的面积”教学设计如下：a.在动态背景下直观感受平行四边形面积大小和高有什么关系。b.在静态背景下体会平行四边形与转化后的长方形有什么关系。将“比较一个长方形框架和由它拉成的一个平行四边形的面积谁大谁小”作为探究的核心问题，让学生经历从猜想到验证的过程，使学生在直观感受平行四边形的面积大小跟什么有关的基础上，自然推出平行四边形面积。

三、进行问题反思，把思维引向深入

为了帮助学生深化所学知识，在帮助学生掌握重点知识的同时，让学生能有更多的收获，教师就可以在带领学生学习完某节课的内容之后，提出能够充分拓展学生思路的问题，帮助学生在反思中发现问题。

例如，“怎样围面积最大”：这类应用题可以通过一个简单的问题，引导学生总结解决这类问题的规律。比如，向学生提问：“用篱笆靠一面墙围成一个面积最大的长方形菜园，怎样围面积最大？”在解决问题的过程中，带领学生总结解决这类问题的规律。通过思考，学生发现，如果用同样长的篱笆靠一面墙围成一个长方形，当这个长方形的长是宽的两倍时，它的面积是最大的；而如果不靠墙，当周长相等时，在所有的长方形中，正方形面积最大。在总结出规律后，就可以让学生进行反思，问学生：“如果不局限于长方形，那么围篱笆时，围成哪种平面图形面积最大？”这时，学生就能结合所学内容进行反思，为之后圆形面积的学习打下基础，这样，在反思中学生获得了更多知识。

思维是数学能力之核，也是数学素养之魂。网状数学课堂应该基于思维教，围绕思维学，让学生获得良好的思维启迪，能自觉地用数学的思维方法去观察、分析社会、解决现实问题，进而提升学习质量、生活质量乃至人生境界。