变间隙磁流变胶泥缓冲器理论研究与试验验证

刘 驰, 付本元, 居本祥, 段俞洲, 王 宏, 张贤明

(1. 重庆理工大学 机械工程学院,重庆 400054;2. 重庆工商大学 废油资源化技术与装备教育部工程研究中心,重庆 400067)

磁流变缓冲器是以磁流变材料作为控制介质的半主动控制器械,主要由缸筒、活塞头、活塞杆及励磁线圈等主要部件构成。磁流变缓冲器具有响应速度快、阻尼力连续可调、动态范围宽等优秀性能,在减振领域应用于轨道车辆垂直减振[1-2]、汽车悬架[3-4]、桥梁斜拉索减振[5]等;在冲击领域被用于汽车碰撞缓冲[6]、火炮反后坐缓冲[7-8]、飞机起落架缓冲[9]、电梯制动缓冲[10]、建筑抗震[11]等。

磁流变缓冲器的结构设计一直以来都被视为磁流变缓冲器能否发挥其优秀性能的重要工作。胡国良等[12]通过改进传统磁流变阻尼器活塞头结构,设计了一种内置阀式磁流变阻尼器,使磁流变阻尼器输出较高的阻尼力,且具备较宽的阻尼可调范围。Fu等[13-15]提出一种多级径向流动节流的磁流变缓冲器,可在受限体积下有效延长阻尼通道长度,提高磁场利用率。董小闵等[16]提出了一种改进的非支配排序遗传算法多目标结构优化设计方案,对磁流变缓冲器的关键几何参数进行优化,达到阻尼力和动态范围最大化。吴欢等[17]在磁路方面进行改进,使得磁路通过梯形截面,增大了磁通量,减少了磁饱和现象,进一步提高了阻尼力利用率。Ichwan等[18]开发了一种新型趋于模块化的磁流变阀。上述研究一定程度上解决了阻尼流道磁场利用率低、有效阻尼长度受限等问题,缓冲器性能得到一定程度提高。但不难发现皆采用等间隙阻尼流道,在冲击时间极为短暂的情况下仅靠励磁电流控制方法实现冲击能量柔顺耗散极具挑战。

为此,在本团队变间隙阻尼流道思路下[19],本文提出了一种缸筒截面具有锥度特征的变间隙磁流变缓冲器,控制介质采用具备优秀悬浮稳定性的磁流变胶泥[20],阻尼间隙随位移增大逐渐减小,以期一定程度上补偿冲击过程中阻尼力衰减。建立双坐标系并分析了动态磁场与位移、电流之间的关系;采用微分思想将变间隙阻尼通道分成若干微元,基于Herschel-Bulkley (HB)本构模型得到单元阻尼通道的速度分布,进一步分析了位移变化对流道截面流速、总压降的影响;考虑局部损耗,构建了HB-Minor Losses (HBM)模型,定量分析了各局部损耗因素的影响比重,并分析了局部损耗压降随位移变化对总压降的影响。制作了变间隙磁流变胶泥缓冲器样机并开展了落锤冲击试验,将HBM模型与试验结果对比,验证了模型预测的准确度。

1 磁流变胶泥的本构模型

磁流变胶泥流变特性在零场和外加磁场作用下皆存在剪切稀化现象。为了更准确地描述磁流变胶泥的流变特性,采用HB模型来描述其本构关系

(1)

磁流变胶泥采用2 Pa·s零场黏度的弹性胶泥为载体液,磁性颗粒体积分数为26 vol%。通过剪切流变仪对不同磁感应强度下磁流变胶泥的流变特性进行测试,采用最小二乘法对数据进行拟合,得到模型参数与磁感应强度关系为

(2)

2 变间隙磁流变缓冲器结构及磁场分析

2.1 工作原理

变间隙磁流变缓冲器结构示意图,如图1所示,主要包括端盖、缸筒、活塞头、活塞杆、密封端盖、受冲端盖等构件。密封端盖A和受冲端盖之间安装弹簧,与活塞杆构成并联关系;活塞头设置两级励磁线圈;缸筒内部填充磁流变胶泥;缸筒截面具有锥度,随着活塞位移增大,环形阻尼通道间隙宽度逐渐减小,同时磁感应强度逐渐增大;缸筒使用20#钢,活塞头使用电工纯铁,均为导磁材料;端盖使用不导磁材料,起隔磁作用。

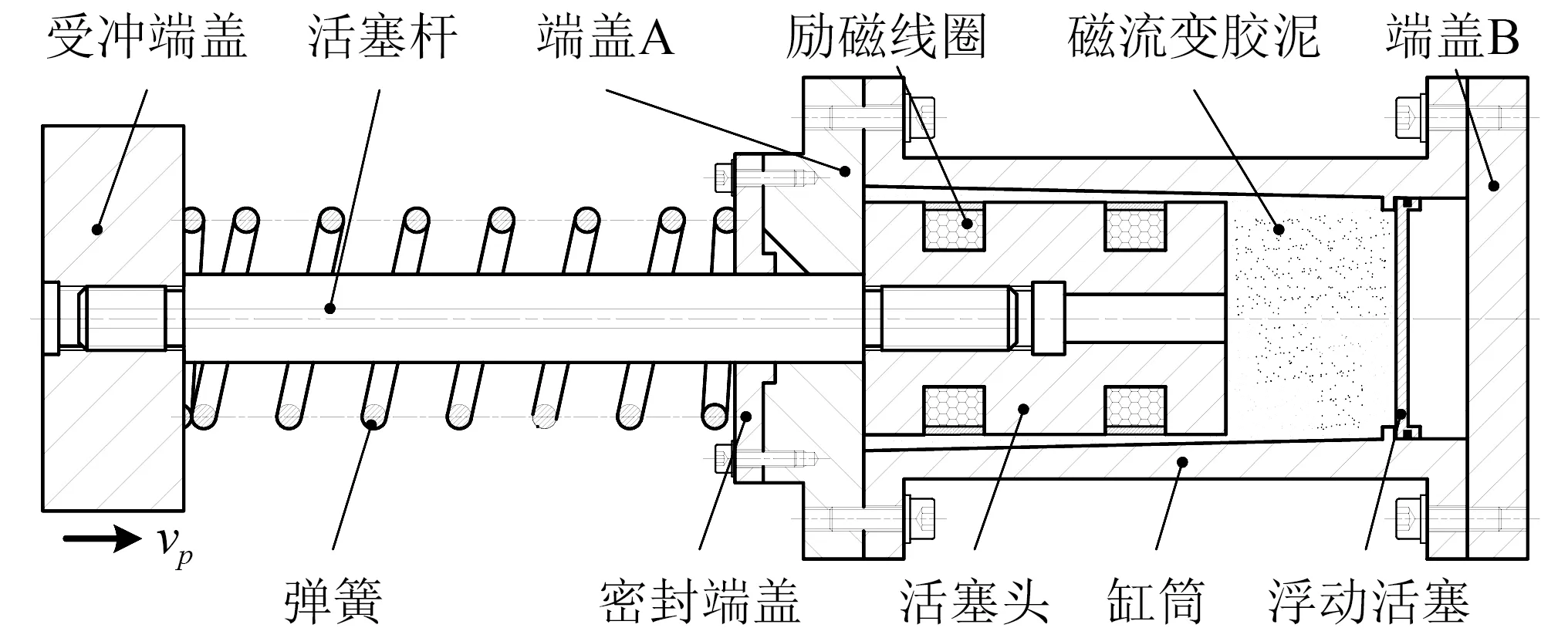
图1 变间隙磁流变缓冲器示意图Fig.1 Schematic of magnetorheological buffer with variable damping gap

2.2 磁路设计

磁路示意图如图2所示,轴向尺寸l1=l2=l3/2=L/6,虚线框所示为磁场线路径,由安培环路定律可知,磁动势可以表示为

图2 磁路示意图Fig.2 Schematic of magnetic circuit

NtI=∮HdLM=Rmφ

(3)

式中:φ=BS;Nt为线圈匝数;I为励磁电流;H为磁场强度;LM为磁场线穿过的长度;Rm为磁路总磁阻;φ为磁通量;B为磁感应强度;S为磁力线穿过区域的面积,磁阻R可以表示为

(4)

式中,μ为材料的导磁率。

线圈1和线圈2产生的总磁阻分别为Rm1和Rm2,皆由六部分磁阻共同组成(见图2),则有

(5)

(6)

缸筒产生的磁阻为

(7)

(8)

磁流变胶泥产生的磁阻为

(9)

(10)

(11)

(12)

活塞头产生的磁阻为

(13)

(14)

式中:d=r1+r2+δ+ltanθ;μ0为真空绝对磁导率;μ1为20#钢的相对磁导率;μ2为磁流变胶泥的相对磁导率;μ3为电工纯铁的相对磁导率。

2.3 磁场分析

为获得磁感应强度与位移的关系,构建双坐标系如图3所示:以端盖A右端面为基准建立xOy坐标系,其中l为活塞位移;以活塞头左端面为基准建立x′O′y′坐标系,其中l′为活塞头各截面到活塞头左端面的距离;依据x′O′y′坐标系将有效阻尼通道内磁感应强度分布划分为①②③三个区域,其中区域①长度范围为0≤l′≤15 mm、区域②为30 mm≤l′≤60 mm、区域③为75 mm≤l′≤90 mm。根据磁场理论分析结果,在位移不变的情况下阻尼流道磁感应强度分布如图4所示,可以看出:各电流下的磁感应强度分布形态相似,即磁感应强度分布形态与电流无关;磁感应强度随电流增大而逐渐增大,但增幅逐渐放缓;由于缸筒截面具有锥度,间隙宽度逐渐减小,每个区域的磁感应强度都呈现递增趋势。

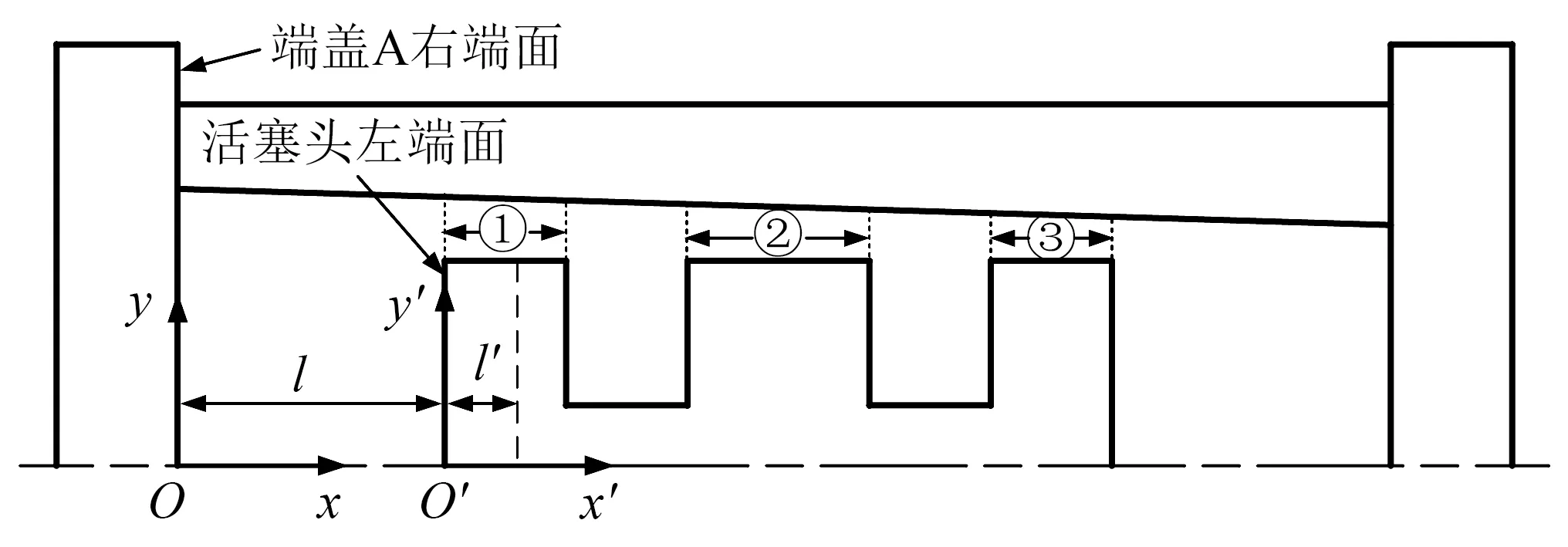
图3 双坐标系Fig.3 Double coordinate system

图4 流道磁感应强度分布Fig.4 Magnetic induction intensity profile in the channel

对比图4(a)～图4(d)可知,当位移逐渐增大时,三个区域磁感应强度皆呈现逐渐增强趋势。为了更显著展示这一结果,在不同位移分别取三个区域的中点位置的磁感应强度进行对比,如图5所示(以5 A电流为例),可以看出,随位移增大,每个区域中点位置的磁感应强度呈上升趋势,说明每个区域磁感应强度在同一电流条件下随位移增大而逐渐增强。

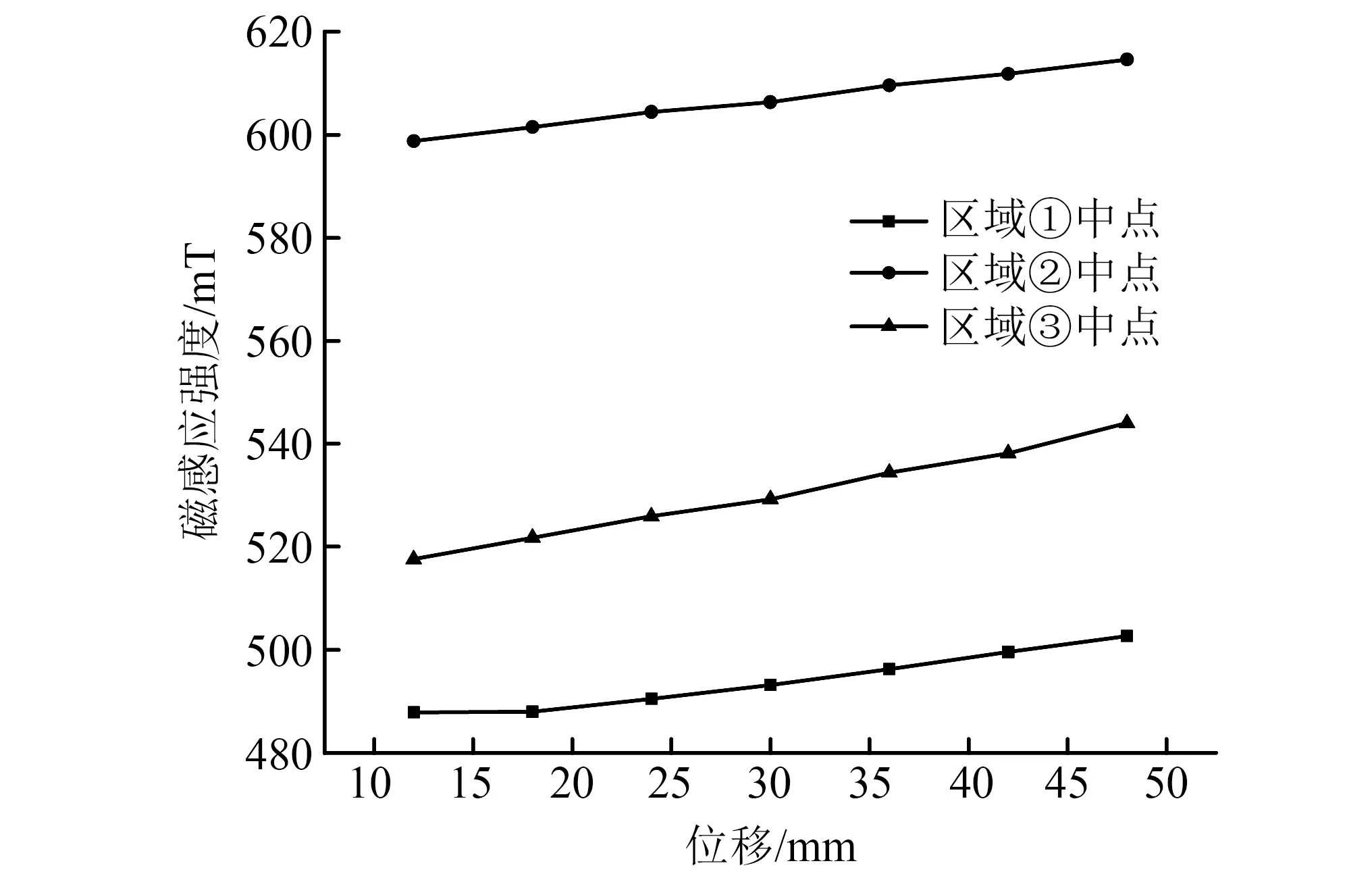
图5 各区域中点磁感应强度与位移的关系Fig.5 Magnetic induction intensity at the midpoint of each region with respect to displacement

对磁场数据进行拟合,得到各区域磁感应强度与电流、位移的关系为:

区域①

(15)

区域②

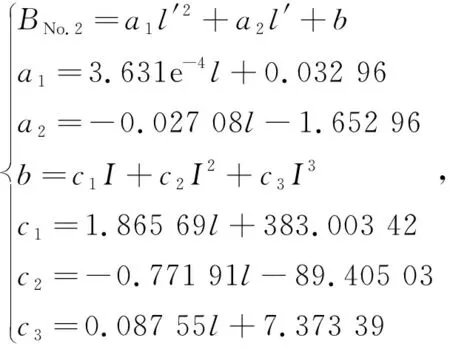
(16)

区域③

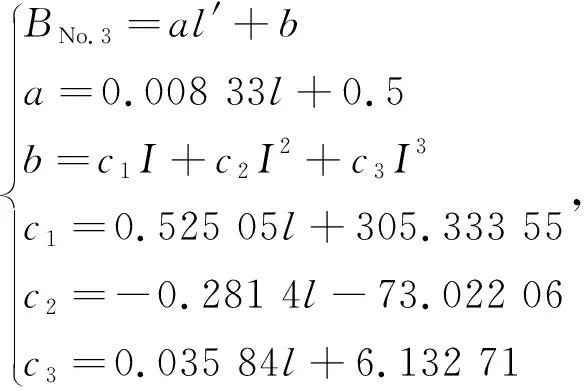
(17)

式中:BNo.1,BNo.2,BNo.3分别为三个区域磁感应强度;I为电流;其余参数均为方程系数。

3 变间隙磁流变缓冲器力学模型

3.1 HB模型

由变间隙磁流变缓冲器结构可知其工作模式为混合模式,因此HB模型总缓冲力FHB由三部分组成:弹簧力Fcs、流动模式阻尼力Fs和剪切模式阻尼力Fv。采用微分思想,将流道总阻尼力转换为若干微元阻尼力叠加进行分析。图6(a)所示为变间隙阻尼流道,沿轴向将其分为N等分微元。由于微元内部间隙宽度变化极小,可将微元视为等间隙流道进行分析,如图6(b)所示,微元流动模式阻尼力为Fse、剪切模式阻尼力为Fve。即

(18)

(19)

故HB模型总缓冲力为

FHB=Fcs+Fs+Fv

(20)

3.1.1 流动模式微元阻尼力

由于阻尼间隙宽度远远小于缸筒内径,可简化为平板模型进行分析,微元间隙宽度为2h(见图6(b))。由于微元视为等间隙宽度,故磁流变胶泥压降在微元内是线性变化的。Fu等同样使用磁流变胶泥作为控制介质,采用HB模型作为本构模型,并将环形流道简化为平板模型,由此引用其环形流道公式得

(21)

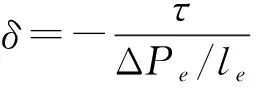
3.1.2 剪切模式微元阻尼力

(22)

3.1.3 弹簧力

根据弹簧设计标准,弹簧力表示为

(23)

式中:λ为总压缩变形(包括预压变形);G为弹簧材料的弹性模量;d为弹簧线径;R为簧圈平均半径;ncs为弹簧的有效圈数(不含支撑部分)。

3.2 HBM模型

由于管道形状和截面宽度的变化,磁流变胶泥在高速冲击流动过程中产生的局部损耗将不可忽略,局部损耗因素主要包括出入口效应、逐渐扩张/收缩、突然收缩/扩张等。局部损耗产生的总压降是所有局部损耗压降的线性组合,因此局部损耗总压降为

(24)

式中:ρ为磁流变胶泥的密度;Km_i为阻尼通道内第i个局部损耗系数;vi为与这个损耗系数对应的流体平均速度。

为减小局部损耗对缓冲器可控性的影响,设计中使用环氧树脂将线圈槽抹平,因而流道内不存在突然扩张/收缩局部损耗因素。流道内局部损耗如图7所示,包括:①入口效应(区域1→2);②逐渐扩张(区域2→3);③出口效应(区域3→4)。因此,局部损耗产生的总压降进一步表示为

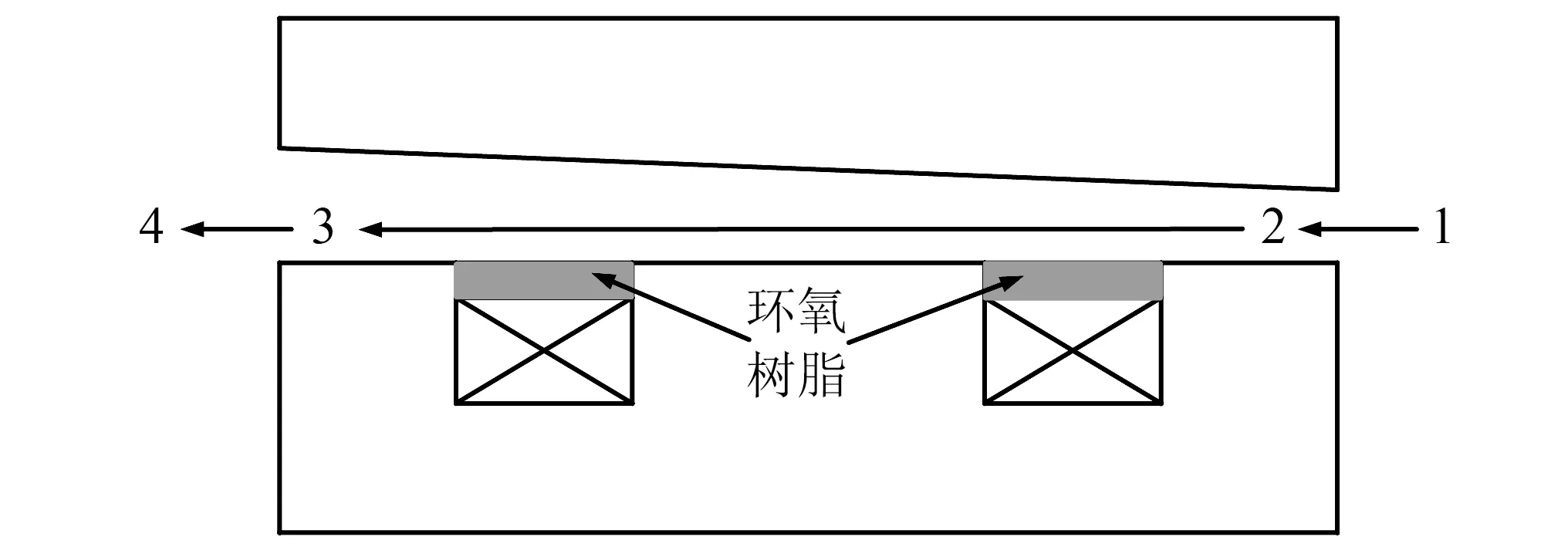
图7 磁流变胶泥流动区域示意图Fig.7 Schematic of magnetorheological cement flow regions

ΔPmin=ΔPmin_1-2+ΔPmin_2-3+ΔPmin_3-4

(25)

式中: ΔPmin_1-2为区域1→2入口效应产生的压降;ΔPmin_2-3为区域2→3逐渐扩张产生的压降; ΔPmin_3-4为区域3→4出口效应产生的压降。

局部损耗压降与阻尼通道的具体尺寸有关,可表示为

(26)

其中,

(27)

(28)

(29)

(30)

故局部损耗产生的缓冲力为

Fmin=ΔPmin·Ap

(31)

综上,HBM模型总缓冲力为

FHBM=FHB+Fmin

(32)

4 试验结果分析

4.1 缓冲器样机与冲击试验条件

为了验证缓冲器动力学特性,制作了缓冲器样机,如图8所示,主要结构参数如表1所示。

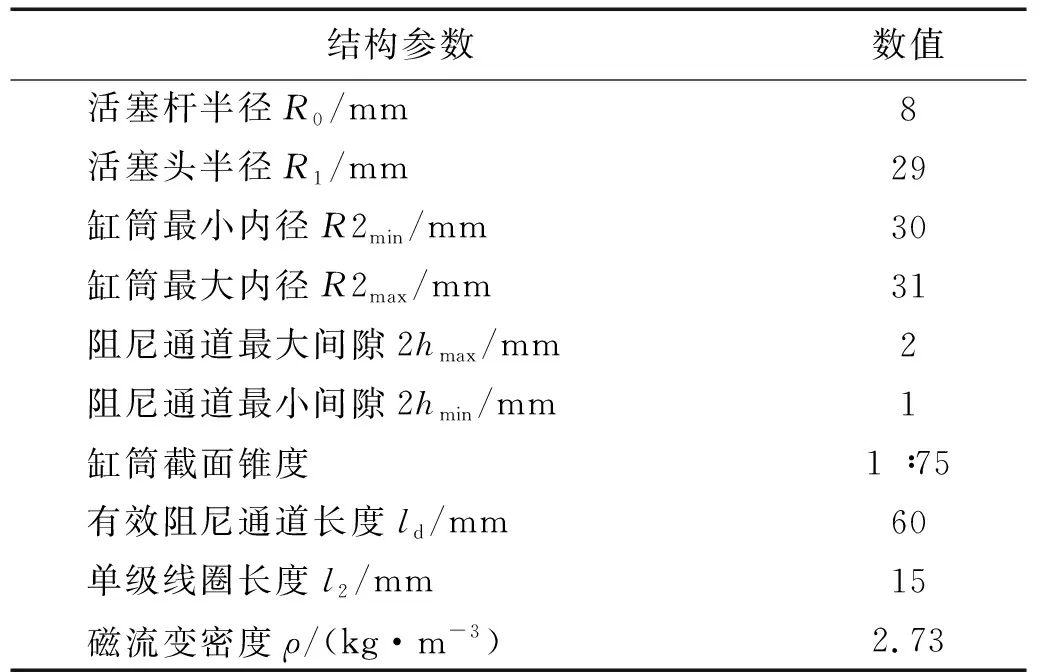
表1 变间隙磁流变缓冲器主要参数Tab.1 Parameters of variable gap MR buffer

图8 变间隙磁流变缓冲器原理样机Fig.8 Photograph of variable gap MR buffer

图9所示为搭建的冲击试验平台,主要包括质量为93.2 kg落锤、压电式力传感器、激光位移传感器、电荷放大器、数据采集卡、励磁电流源等。试验中,采集频率设定为10 kHz,设置不同励磁电流和冲击速度,试验条件如表2所示。

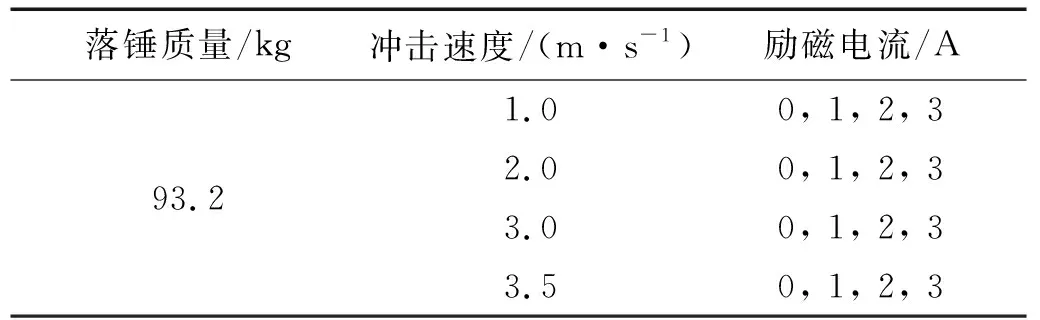
表2 试验条件Tab.2 The conditions of test

图9 冲击试验平台Fig.9 Drop tower test system

4.2 基于HBM模型流道分析

4.2.1 流速分析

变间隙磁流变缓冲器,由于间隙宽度发生变化,导致截面流速发生变化,取区域②中点截面为例进行分析,图10为理论截面流速与位移、间隙宽度的变化关系。从图10(a)可以看出:由于屈服区的剪切应力小于屈服应力,导致截面流速在屈服区向边界逐渐较小;由于靠近边界越近剪切应力越大,导致截面流速越靠近边界减小的越剧烈;位移从0逐渐增大到60 mm时,间隙宽度会逐渐减小,其中2 m/s &3 A时从1.7 mm逐渐减小至1.3 mm,表明阻尼间隙逐渐收窄。由图10(b)可知,随着阻尼间隙收窄,截面流速会逐渐增大,2 m/s &3 A时刚性流动区域流速随之从22.72 m/s增大到30.09 m/s(见图10(b)),表明减小流道间隙宽度可以在冲击环境下一定程度补偿流速衰减。图10(c)展示了刚性流动区域厚度与位移的关系,可以看到,随位移逐渐增大,刚性区域厚度逐渐减小,其中2 m/s &3 A时从0.108 mm减小至0.061 mm。另外,由图10(b)和图10(c)可知,冲击速度与励磁电流也会影响刚性区域速度、厚度:对比3.5 m/s &3 A及2 m/s &3 A发现,增大冲击速度会增大刚性区域速度并减小厚度,主要是因为增大冲击速度会增大磁流变胶泥在流道内的剪切应力;对比2 m/s &3 A及2 m/s &0发现,增大励磁电流会减小刚性区域速度并增大厚度,主要原因是增大励磁电流会增大磁流变胶泥屈服应力。

4.2.2 总压降分析

流道总压降由流动模式、剪切模式、局部损耗共同产生,图11为理论流道总压降与位移的关系,可以看出:①总压降随位移增加逐渐增大,且增幅逐渐变大,在位移达到60 mm时,3.5 m/s &3 A条件下总压降可达61.6 MPa。主要原因是:由于间隙宽度逐渐减小,导致流道磁感应强度逐渐增大,需要更大的剪切应力用于破碎磁流变胶泥磁链;同时随位移增大会增大流速,而局部损耗压降与流速平方成线性关系,导致局部损耗压降非线性增长。表明减小流道间隙宽度可以在冲击环境下补偿部分缓冲力衰减。②对比3.5 m/s &3 A及2 m/s &3 A可知,增大冲击速度会增大总压降,原因是增大流道内黏滞阻尼力及局部损耗压降;对比2 m/s &3 A及2 m/s &0可知,增大励磁电流也会增大总压降,主要是因为增大励磁电流会增大有效阻尼流道内磁控阻尼力。

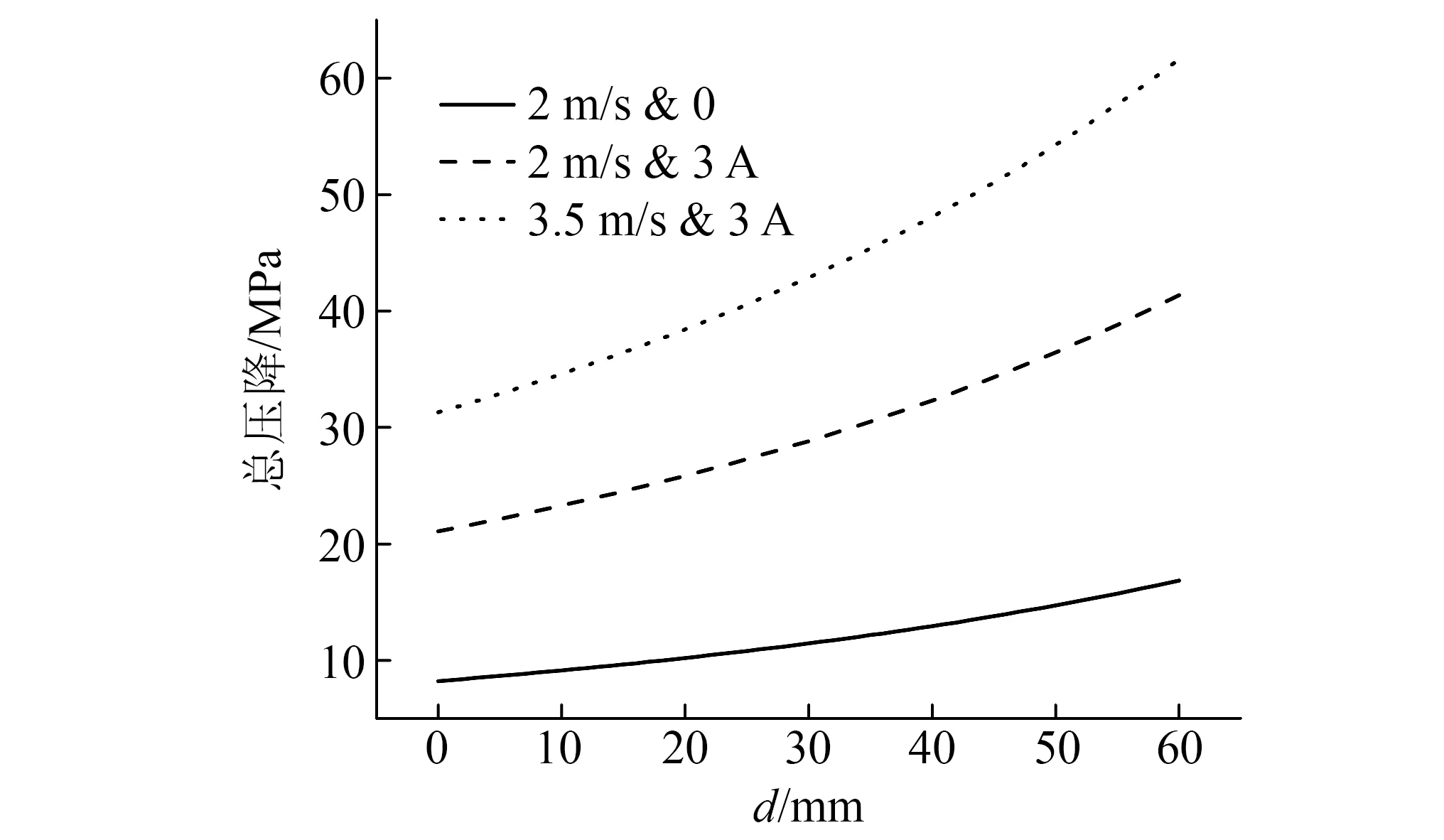
图11 HBM模型中总压降vs位移Fig.11 Pressure drop with respect to displacement in HBM model

4.2.3 局部损耗影响分析

局部损耗压降是影响磁流变缓冲器可控性的重要因素。局部损耗与结构尺寸有关,在活塞运动过程中流道截面积随之发生变化,进而影响局部损耗压降在总压降中比例。图12(a)为HBM模型中局部损耗压降在总压降中占比情况,可以看到:①随位移从0增加至60 mm,局部损耗压降在总压降中所占比例逐渐减小,其中2 m/s &0条件下从7.51%减小至6.54%,主要是因为流道间隙减小导致的局部损耗压降增幅弱于流动模式及剪切模式压降增幅,表明逐渐减小流道间隙的结构设计可以弱化局部损耗的影响,进而对缓冲器的可控性具有优化作用。②3.5 m/s &3 A条件下局部损耗压降占比大于2 m/s &3 A,主要是因为局部损耗压降与速度二次方成正比,随速度增长幅度大于总压降增长幅度,说明增大冲击速度会增大局部损耗压降占比。③2 m/s &3 A条件下局部损耗压降占比小于2 m/s &0,主要是因为增大励磁电流会增大有效阻尼流道内磁控阻尼力,说明增大励磁电流会减小局部损耗压降占比。图12(b)为各局部损耗因素产生的压降在总局部损耗压降中的占比,从图12中可以看到,入口效应和出口效应产生的压降所占比重较高,分别为53.7%和45.5%;逐渐扩张产生的压降仅占0.77%,相比出入口产生的压降可以忽略,故而若进一步提高缓冲器的可控性,需在流道出入口进行优化。

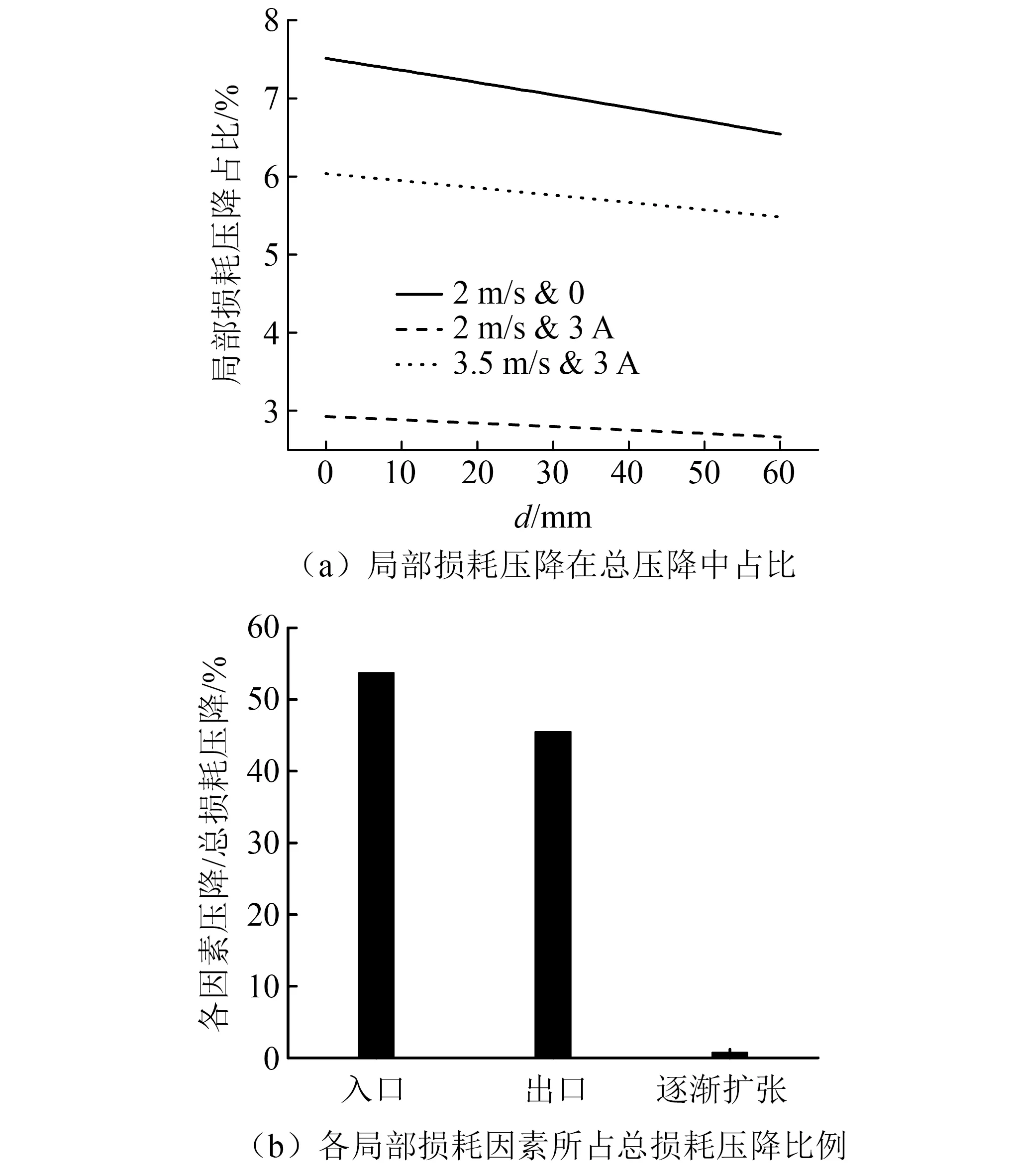
图12 局部损耗对压降的影响Fig.12 Effect of minor losses on pressure drop

4.3 试验结果分析

按照表2试验条件开展冲击试验,不同冲击速度下缓冲力时间历程如图13所示,可以看出:①相同冲击速度下,随着励磁电流增大,峰值缓冲力均明显增大,说明变间隙磁流变缓冲器具有良好的磁控特性;同时峰值力到达时间随励磁电流增大而呈减小趋势,这是因为增加励磁电流会增大流道压降,进而增大了缓冲器的平均缓冲力,导致冲击过程中落锤减速度增大,因此冲击速度相同的情况下,励磁电流越大峰值力到达时间越短;②励磁电流相同时,随着冲击速度的增大,落锤动能变大,缓冲力呈增大趋势。

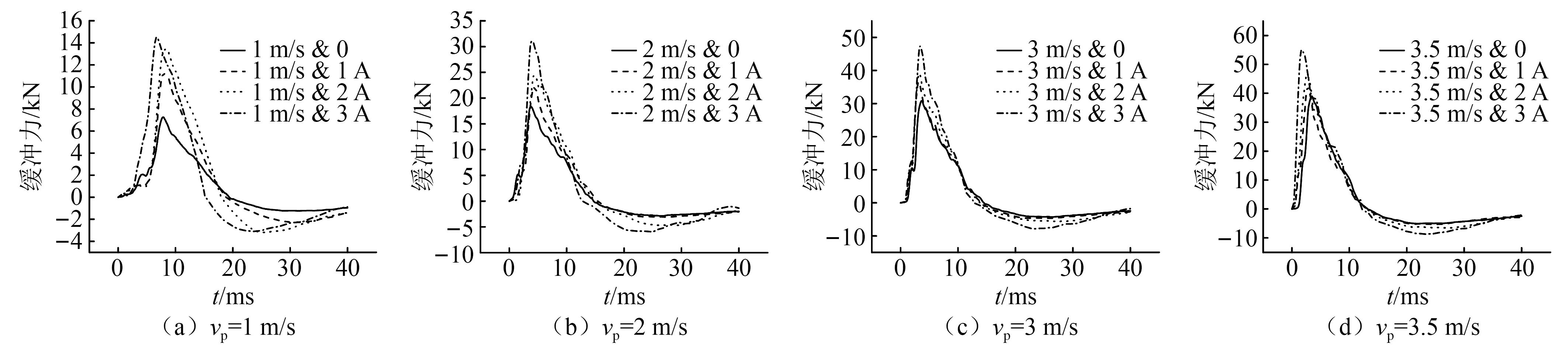
图13 不同冲击速度下缓冲力时间历程Fig.13 Time history of the force at different velocity

4.4 模型准确性验证

为了验证模型的准确性,以3.5 m/s速度为例进行分析,将理论缓冲力时间历程与试验进行对比,如图14所示。从图14中可以看出,HBM模型缓冲力时间历程和试验数据趋势基本一致,但两者还存在一定差异:试验数据不如HBM模型曲线那么滑顺,主要原因是试验过程中不可避免的出现振动;HBM模型缓冲力整体略低于试验结果,这是因为实际中会存在惯性效应而理论中并未考虑到;HBM模型峰值到达时间比试验晚几毫秒,主要原因是HBM模型中虽然考虑了剪切稀化效应,但由于流道真实剪切率远大于材料测试的剪切率,导致材料本构模型参数在冲击环境存在一定偏差。

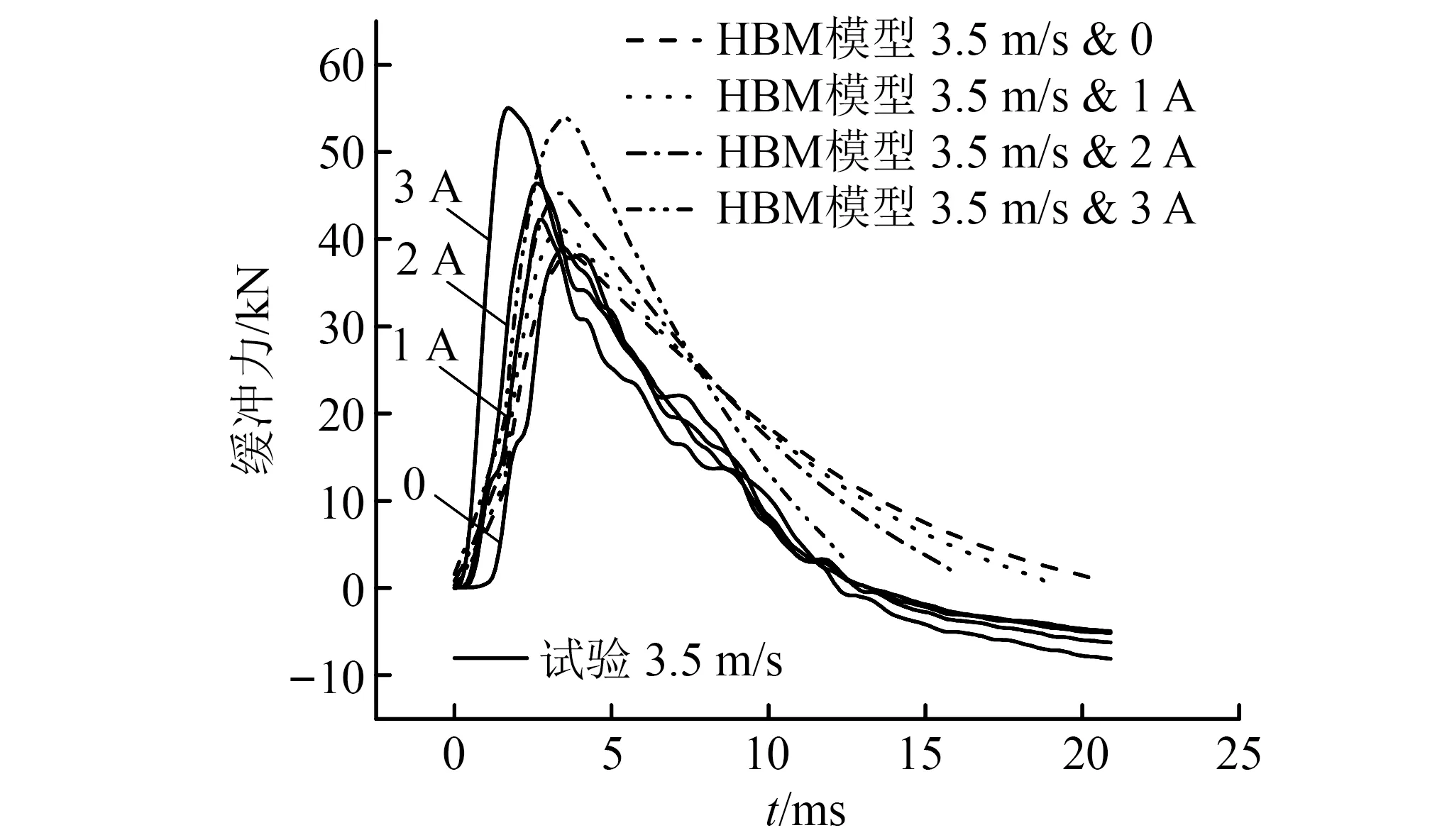
图14 冲击速度为3.5 m/s时,试验和理论缓冲力时间历程Fig.14 Theoretical and experimental time history of the force at different velocity at the velocity of 3.5 m/s

峰值力和动态范围是表征变间隙磁流变缓冲器动态性能的重要指标。图15(a)为理论试验峰值力对比情况,可以看出:试验和理论峰值力都随冲击速度增加而增大,原因是较高的冲击速度具备更大的冲击能量,导致缓冲力增大;峰值缓冲力随冲击速度增大趋势基本呈现线性,主要是因为流道内局部损耗对总压降影响较小;试验和理论峰值力都随励磁电流增加而增大,例如电流从0依次增加到3 A,3.5 m/s时峰值力在相邻电流间依次递增8.3%,9.8%,18%,原因是增大励磁电流会增强流道内磁感应强度,进而增大流道压降;理论峰值力与试验峰值力之间的偏差较小,但两者的偏差随速度增大而逐渐增大,这是因为HBM模型并未考虑惯性效应,而增大速度会加强惯性效应的影响。图15(b)为试验和理论动态范围对比情况,可以看出:理论和试验动态范围曲线基本一致;速度从1 m/s增加到3.5 m/s时,动态范围逐渐减小,其中试验动态范围从2.0逐渐减小至1.4,这是由于增大速度会急剧增大局部损耗及黏滞阻尼力而可控阻尼力并未明显增加。

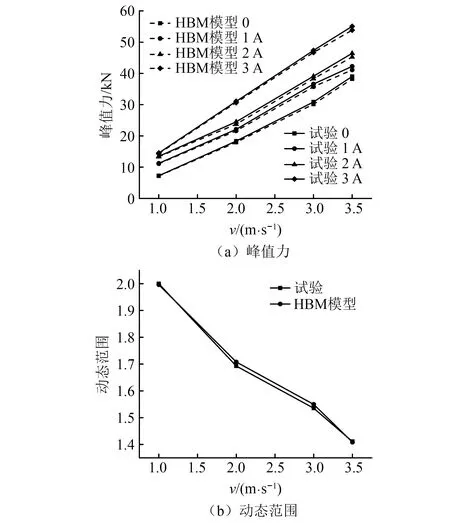
图15 理论与试验结果对比Fig.15 Comparison between theoretical and experimental results

5 结 论

(1) 设计了一种变间隙磁流变缓冲器,其间隙宽度随位移位移增大逐渐减小;采用双坐标系分析了动态磁场,三个区域磁感应强度皆随着间隙减小逐渐增大;采用微分思想,基于HB模型得到了微元阻尼通道的微分方程,并充分考虑局部损耗,构建了HBM模型。

(2) 变间隙磁流变缓冲器流道截面流速随着位移增大而增大,同时刚性流动区域厚度逐渐减小;总压降随位移增加而增大,3.5 m/s &3 A时总压降于位移为60 mm处可达61.6 MPa;局部损耗压降在总压降中占比随位移增大逐渐减小,其中2 m/s &0时从7.51%减小至6.54%。三个流道参数均表明减小间隙宽度的流道结构可以在冲击环境下补偿流速衰减导致的缓冲力衰减,有利于实现冲击能量的柔顺耗散。

(3) 搭建了冲击试验平台,在1 m/s,2 m/s,3 m/s,3.5 m/s四种冲击速度下分别施加0,1 A,2 A,3A励磁电流进行试验,结果显示峰值力最高可达55 kN、动态范围最大可达2.0,表明缓冲器具有良好的可控性;进一步从缓冲力时间历程、峰值力、动态范围三个方面对比了HBM模型与试验结果,发现HBM模型可以准确描述变间隙磁流变胶泥缓冲器冲击动力学行为。