结构模态多级分层并行计算方法

喻高远, 楼云锋, 李俊杰, 金先龙

(1. 上海交通大学 机械与动力工程学院,上海 200240;2. 上海宇航系统工程研究所,上海 201108)

随着科学研究和工程技术的不断发展,出现了诸如高速动车组、3 000 m超深钻机、大飞机、大功率海洋压缩机等复杂装备系统及跨江隧道、摩天大厦等大型和超大型工程系统[1]。这些系统安全性和稳定性等方面的苛刻要求对其动力学系统性能数值模拟提出了严峻的挑战,其整体有限元系统建模需要考虑精细建模以反映局部响应,致使其有限元系统自由度规模巨大,求解复杂[2-4]。在这些复杂动力学系统的计算过程中,模态分析是其最耗费时间的环节,也是其余计算环节的基础,需借助大规模有限元模型进行高精度模态计算。这些问题在传统的串行机上无法得到满意的解答[5-6]。随着超级计算机的快速发展和大量先进算法的涌现,利用其研究和开发相应的大规模模态并行算法则为这类问题的解决提供了切实可行的方法。

模态分析的数学实质可以归结为大型稀疏矩阵的广义特征值问题[7-8],其求解方法主要有Lanczos算法[9]、Arnoldi算法[10]、Krylov-Schur算法[11]等。各国学者在Lanczos算法、Arnoldi算法、Krylov-Schur算法等的基础上进行了一系列的模态并行算法研究,主要集中在:从模态有限元分析中耗时最多的线性方程组求解出发寻求高效率求解线性方程组的并行计算方法和从有限元问题自身的并行性出发形成的模态综合法两大类并行计算方法[12]。直接法和迭代法是模态并行求解的两种基本算法。直接法通过排序、三角分解和回代计算能够在预期内得到方程的解。然而,随着有限元计算规模的增加,其所需的内存空间和计算量也会显著增加。迭代法通过多次迭代对求解结果进行改善以达到收敛容差范围,求解过程中所需内存小,容易实现并行化。但迭代法无法保证收敛的合理时间,且对于条件数很大的病态问题也可能是不收敛的。在模态综合并行计算方面,各国学者将直接法和迭代法混合并从有限元问题自身的并行出发,将复杂模态求解问题拆分为一个个较小的子模态问题进行并行处理,子问题模态求解过程中方程求解采用直接法,通过2次模态坐标变换得到缩聚后的系统级模态广义特征方程以降低其整体规模,然后缩聚后的系统级模态广义特征方程中涉及线性方程组的求解采用迭代法,因而能够很好地利用直接法和迭代法的优点提高并行效率,在结构模态并行求解领域得到了广泛的应用。Rong等[13]基于模态综合法和传递矩阵法完成了大规模特征值的混合并行求解设计,并将其应用于某真空容器的大规模模态并行求解。Heng等[14]基于模态综合法利用共享式存储并行计算机完成了某悬臂梁的大规模模态并行求解。Aoyama等[15]通过改进模态综合法各子系统界面的耦合方式完成了某矩形板的大规模模态并行求解。Părík等[16]采用模态综合法基于OpenMP完成了模态并行计算求解体系设计,并利用其完成了某轴系的模态并行求解。然而对于大规模问题采用模态综合法进行并行求解时,随着子区域数目的增多,缩聚后所得系统级模态广义特征方程的规模和条件数也随之急剧增加,从而给求解带来了困难。另外,在迭代求解系统级模态广义特征方程时,由于所有的进程都需要参与全局通信,进程间通信和同步开销的增加也会极大地降低并行效率。

在硬件方面,科学和工程计算中使用最广的并行计算机为分布式存储并行计算机,其体系架构主要包括纯CPU的同构型超级计算机[17]和异构型超级计算机[18]。异构型超级计算机以其高性价比、强计算能力等优势,已成为目前分布式存储并行计算机的主流架构。对于异构型分布式存储并行计算机来说,最为重要的部分就是集群环境下的不同存储机制、处理器之间的相互通信与协作以及各级硬件体系结构的负载均衡,这也是影响并行效率很重要的因素。因此,利用异构型分布式存储并行计算机提高并行效率的关键在于处理好计算任务与异构集群硬件拓扑体系结构适配时的负载均衡、大规模数据的存储以及处理器间的相互通信和协作问题。

为解决采用模态综合法利用大量异构核组求解大规模模态问题并行求解效率低的问题,本文在稀疏存储和传统并行模态综合法的基础上提出了一种结构模态多级分层并行计算方法。采用两级分区4次变换,降低系统整体缩减后的广义特征方程规模。

1 模态综合法

在传统的并行模态综合法中[19-20],有限元网格仅被剖分1次,然后在生成的m个子区域上按照先内部自由度I集后边界自由度B集的编号原则,组集每个子区域系统的质量矩阵Msub和刚度矩阵Ksub。进行第1次坐标变换时,各子区域系统物理坐标与模态坐标之间的关系可以表示为

(1)

式中:UI,UB,{pk},{pB}分别为内部节点和边界节点对应的位移和模态坐标;[Φ]为子区域的模态转化矩阵;[ΦIk]为内部节点主模态矩阵;[ΦIB]为约束模态。

利用各子区域系统之间的位移协调条件,进行第2次坐标变换,如式(2)所示

(2)

K*φ*=λ*M*φ*

(3)

缩减刚度矩阵[K*]和缩减质量矩阵[M*]为

(4)

采用并行Krylov子空间迭代法求解式(3)即可获得整体系统所需要的低阶模态频率和模态振型,将其代入式(1)即可得各子区域的模态振型。

2 分层并行计算方法

分层并行计算方法通过两级分区4次变换在分布式数据稀疏存储和传统并行模态综合法的基础上通过并行任务映射既改善了不同层级的负载均衡,又实现了通信分离有效提高了通信效率。此外,它还进一步降低了界面方程的规模,加快了其迭代收敛速度。

2.1 并行任务映射

通过将计算任务映射到异构众核超级计算机的不同硬件层,以实现不同层级的负载均衡和通信的有效分割。在传统并行模态综合法的基础上,考虑“神威太湖之光”异构众核超级计算机的硬件体系架构,完成结构大规模模态分层并行计算任务映射,如图1所示。

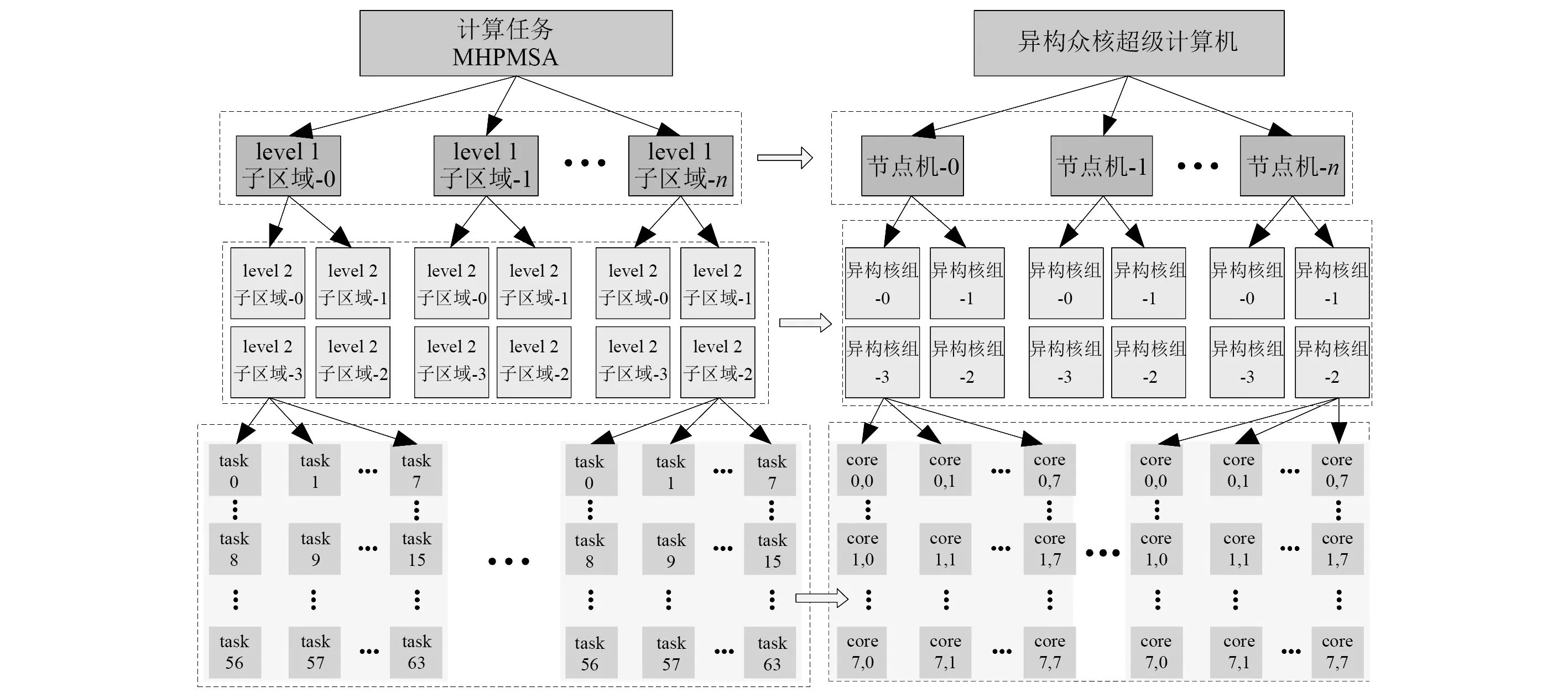
图1 结构模态多级分层并行模态综合法计算任务映射Fig.1 Task mapping of multilevel hierarchical parallel modal synthesis algorithm

在进行任务映射时,将第1级网格子区域按照节点顺序进行映射,第2级网格子区域按照节点内异构群组进行映射,各异构群组内浮点运算按照计算核心进行映射。

2.2 两级分区

在两级分区中,首先采用开源并行有限元分区程序ParMETIS将有限元网格剖分为p个1级子区域,然后每个1级子区域再进一步按照异构众核体系架构特点剖分为m个2级子区域。为与“神威太湖之光”异构众核分布式存储超级计算机相适配,p应为并行计算每次启动节点机总数,m应为单个节点机内异构核组的数量,为4。如图2所示,若p为2,则有限元网格先被剖分为2个1级子区域,然后每个1级子区域又被剖分为4个2级子区域。

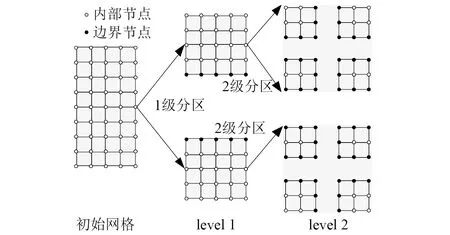
图2 2级分区Fig.2 Two-level partitioning

2.3 4次变换

4次变换通过先后在2级子区域和1级子区域上应用式(2)和式(4)实现变换过程,如图3所示。首先,形成每个2级子区域系统的质量矩阵和刚度矩阵,并通过第1次坐标变换构成仅包含内部自由度的广义特征方程,通过子区域凝聚得到各子区域的等效刚度矩阵和等效质量矩阵;然后,通过组集隶属于相同1级子区域内的所有2级子区域等效刚度矩阵和等效质量矩阵,并通过第2次坐标变换得到仅含有独立坐标的1级子区域广义特征方程;最后,通过凝聚、组集和坐标变换得到仅含有独立坐标的系统整体的广义特征方程。

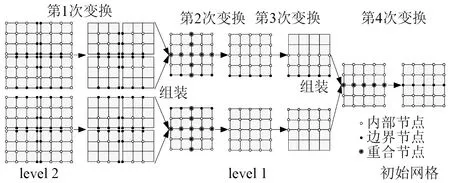
图3 4次变换Fig.3 Four transformations

为改善计算过程中的内存访问速率,考虑到申威异构众核处理器各核组配置有8 G私有内存且均可独立访问,在进行计算时,各子区域的数据信息均通过多文件流存储在相应的节点机内各异构核组上。此外,相对于传统并行模态综合法,分层并行计算方法通过4次变换2次凝聚进一步降低了系统整体广义特征方程的规模,加快了其迭代收敛速度。

2.4 三层并行计算机制

考虑异构众核分布式存储并行计算机的通信特点,控制通信协作以提高通信效率的关键在于实现节点内通信和节点间通信分离、节点内异构核组内通信和节点内异构核组间通信分离以及减少系统整体求解进程间的通信和同步开销。即要根据异构众核分布式存储并行计算机的通信结构将大量局部通信限制在节点内,并最大限度减少不同节点间的全局通信。而分层并行计算方法刚好满足这些条件,如图4所示,它是在两级分区4次变换策略的基础上实现了计算过程的三层并行。

图4 三层并行机制Fig.4 Scheme of three-layer parallelization

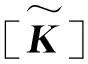
为节省内存空间和减少计算量,各2级子区域局部总体刚度矩阵和总体质量矩阵均采用列压缩稀疏存储格式进行存储。

第2层并行,各节点机内分别同时进行相应1级子区域的组集、并行凝聚和回代求解,通信存在于同一节点内的不同异构核组之间及各异构核组内运算控制核心和计算核心之间。计算过程中的数据采用列压缩稀疏存储技术进行分布式存储,在进行计算时,由各节点机内的0号异构核组负责相应1级子区域的组集、数据分发、并行凝聚结果的汇总和内部回代求解。各节点机内对应1级子区域的并行计算过程则由同一节点机内所有的异构核组同时参与,1级子区域对应的广义特征方程(KII,MII)采用并行Lanczos方法进行求解,求解时涉及的线性方程组采用并行预处理Cholesky分解。

第3层并行,利用并行Krylov子空间迭代法求解系统整体的缩减广义特征方程,每个节点机仅有1个核组-0号异构核组参与求解和通讯,如图5所示。在进行求解时,系统整体的缩减刚度矩阵[K*]和缩减质量矩阵[M*]仍分布式存储在各节点机0号异构核组对应的内存空间当中,中间计算结果也以列压缩格式进行分布式存储。大量的局部通信存在于各异构核组内运算控制核心和计算核心阵列之间,只有少量的点积操作和整体迭代误差的计算需要全局通信。因而它能够有效减少通信量,提高并行计算效率。

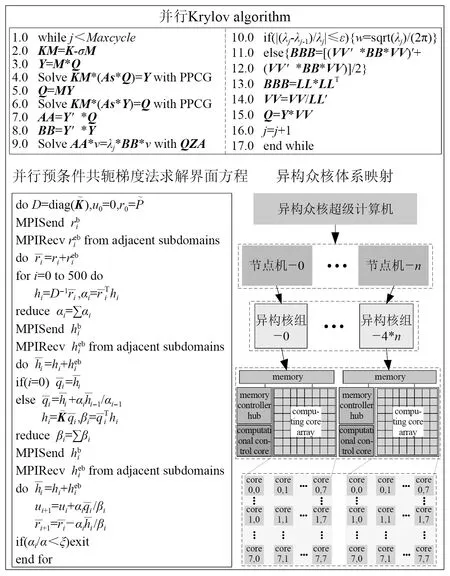
图5 并行Krylov算法及其任务映射FFig.5 Parallel Krylov algorithm and task mapping

3 算例验证

为验证所提算法的正确性和有效性,采用“神威太湖之光”超级计算机进行测试,测试时每个节点启动4个异构核组。采用所提算法和传统并行模态综合法,进行某超深钻机盘鼓式制动器转子盘模态分析,其有限元网格模型如图6所示,该模型具有2 896 781个实体单元、自由度规模为6 176 367、刚度矩阵非零元个数为501 507 352、平均带宽为260。固定约束其内表面8个螺栓孔位置,计算结构的前20阶固有频率,并与经典模态求解算法-Lanczos算法[9,19]的求解结果进行对比。测试所得的前20阶固有频率的最大相对误差按照式(5)计算

图6 某转子盘有限元系统Fig.6 Finite element of rotor system

(5)

经计算后可知,采用本文算法与传统并行模态综合法所得模态频率的计算结果与经典Lanczos算法的相对误差均小于0.7%,各阶振型保持一致,有效验证了本文计算结果和传统并行模态综合法计算结果的正确性。

通过启动相应数目的节点机测试本文分层并行计算方法和传统并行模态综合法的性能。测试时,启动节点机总数依次为16,32,64,128。由于两级分区时相应1级子区域总数应分别等于每次启动节点机总数,故相应1级子区域总数也依次为16,32,64,128。因“神威太湖之光”超级计算机每个节点包含4个异构核组,故2级剖分时每个1级子区域被独立地剖分为4个2级子区域。制动盘的并行计算结果如表1所示。

表1 制动盘并行效率计算结果Tab.1 Results of parallel computation for rotor of brake system

表1中,并行计算总时间包含各子区域系统开始计算到各子区域系统模态振型求解结束。1级子区域求解时间包括组集1级子区域等效刚度矩阵和等效质量矩阵的时间、1级子区域凝聚缩减的时间、并行求解方程的时间和回代1级子区域模态坐标的时间。由表1可知,相对于传统的并行模态综合法,本文提出的分层并行计算方法能够获得较高的加速比和并行效率。这是由于采用传统的并行模态综合法时,随着子区域数目的增多,形成的整体广义特征方程的规模和条件数也随之急剧增加,导致了界面方程求解时间的大幅度增加,从而严重影响了系统总体并行效率的提高。从数学的角度看,分层并行计算方法1级子区域的求解实质上是在求解和传统并行模态综合法相同规模的系统广义特征方程,但其求解时间却大大缩短了。例如在表1中,512计算核组时1级子区域的求解时间为732.1 s,而传统并行模态综合法的系统方程求解时间为2 021.2 s,这就节约了1 289.1 s。主要原因在于:分层并行计算方法通过两级分区4次变换不仅将节点内通信与节点间通信分离以及节点内异构核组内通信与异构核组间通信分离有效改善了通信效率,而且它还进一步降低了凝聚后系统方程的规模,加快了其计算和迭代收敛速度。从负载均衡与异构型超级计算机适配的角度来看,本文将有限元计算的结构任务划分为节点间并行、节点内核组间并行、核组内各计算核心间并行。由于初始1级子区域计算规模都相同,且各节点机具有相同的计算性能,这就实现了节点间的负载均衡和并行计算。2级子区域按照节点机内核组的数量进行划分,与传统并行模态综合法相比,本文直接参与并行计算的子区域数目通过两级分区降低为其1/4。子区域数目的降低一方面有利于降低界面方程的规模和条件数,从而有效提高系统的数值收敛性;另一方面有利于大幅度减少参与并行计算的进程数目,从而减少因通信竞争造成的各核组间的计算资源浪费。同时,核组内各计算核组间的并行可以充分利用2级子区域对应的所有计算核心共享的内存空间,有效提高数据的访问速度和计算效率,且能够避免因分区过多导致的系统数值收敛性降低和通信开销增加带来的负载均衡问题。因此,它能够有效减少1级子区域求解时间,并获得良好的加速比和并行效率。

在实际的工程应用中,有时复杂工程结构会包含多种单元类型,为测试多单元混合建模千万自由度规模下复杂工程系统的并行效率,以如图7所示的某跨江隧道模型为例进行分析,该模型具有2 896 781个实体单元、186 121个梁单元、21 685个质量单元、自由度规模为13 167 203、刚度矩阵非零元个数为1 012 581 369、平均带宽为412,求解其前20阶固有模态频率。

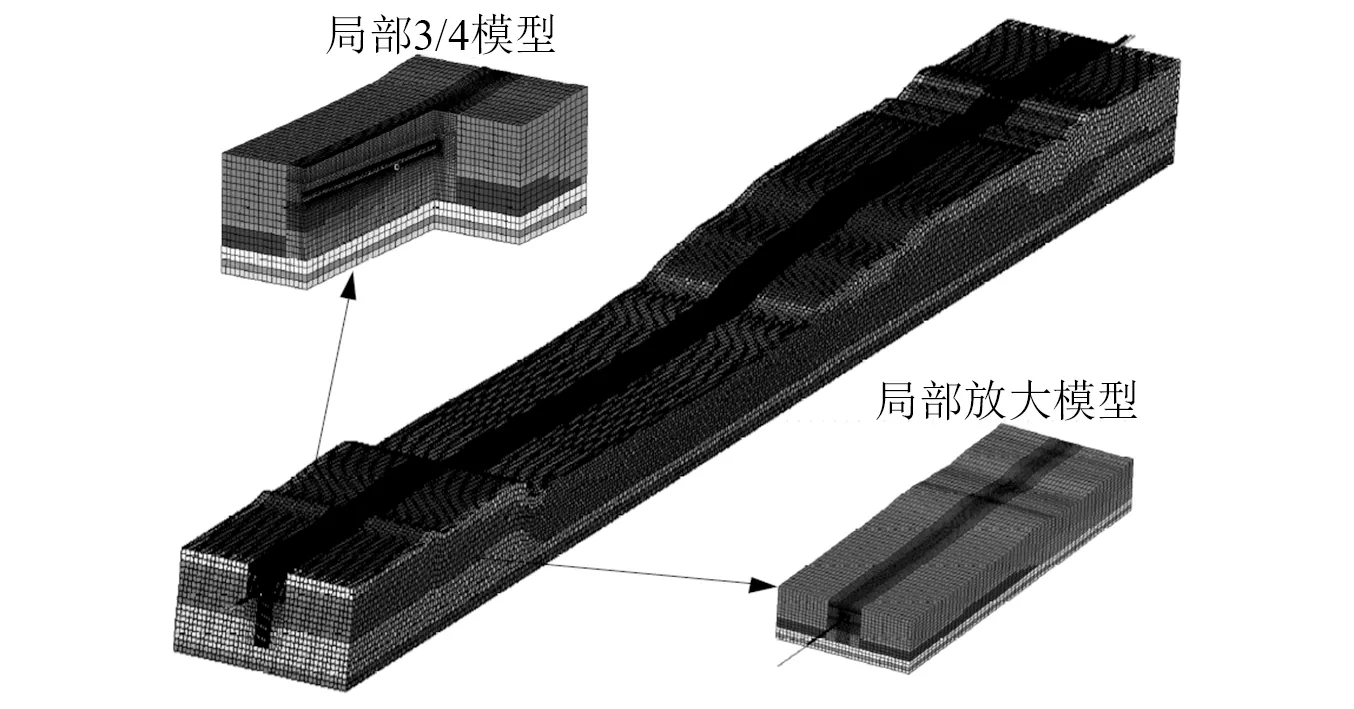
图7 某跨江隧道结构有限元系统Fig.7 FEM of the over-river tunnel structure system

并行计算时启动节点机总数依次为32,64,128,256。采用传统并行模态综合法和本文多级分层并行计算方法的计算结果如表2所示。

表2 某跨江隧道的并行计算结果Tab.2 Results of parallel computation for over-river tunnel

由表2可知,对于传统的并行模态综合法,当整体系统方程采用直接法进行求解时,随着子区域的增多整体系统方程的求解时间大幅度增加,从而严重降低了系统的并行效率。这是由于虽然总体界面方程采用稀疏列压缩格式存储,且三角分解时利用并行预处理Cholesky分解只对下三角部分进行分解,但是总体界面方程是高度稠密的,其进行三角分解时会增加原有方程的稠密度,致使其组集和三角分解不仅需要申请大量的内存,而且需要大量的通信和计算。随着子区域的增多,系统整体缩减后的广义特征方程规模随之增大,由此带来的存储、通信和计算开销也就越来越大,系统整体的求解时间也就越长。而采用分层并行计算方法时,由于利用迭代法求解不需要组集形成系统缩减后的广义特征方程。另外,涉及方程组并行求解时的局部通信仅存在相邻子区域之间,只有少量的向量运算和整体迭代误差的计算需要全局通信。因此,它能够以较短的求解时间获得较高的加速比和并行效率。

4 结 论

(1) 为解决采用模态综合法利用异构众核分布式存储并行计算机求解大规模有限元模态对计算效率造成的损失,在吸收和利用稀疏存储技术和传统并行模态综合法优点的基础上提出了一种基于稀疏存储格式的结构有限元模态多级分层并行计算方法。

(2) 通过典型数值算例表明,与传统的并行模态综合法相比,该方法能够获得更高的加速度比和并行计算效率,并大幅度节省内存空间。

(3) 本文的研究结果将为结构有限元软件在国产异构众核处理器和其他异构处理器上的移植及大规模并行提高参考,对重大装备系统及复杂工程系统的研制和使用均具有较强的指导意义和参考价值。