VMD-PSO-LSTM 模型的日径流多步预测
王秀杰,王 玲,滕振敏,田福昌,袁佩贤,苑希民
(1. 天津大学 水利工程仿真与安全国家重点实验室,天津 300072; 2. 崇左市左江治旱工程管理中心,广西 崇左 532200; 3. 北京城建设计发展集团股份有限公司,北京 100032)
准确可靠的径流预测对合理利用水资源、提升防洪减灾能力及充分发挥水库的综合效益具有重要意义。但受气候变化和人类活动等因素的综合影响,径流变化具有较强的非线性和不确定性,为水文预报带来困难。因此,提高水文预报精度一直是水文水资源领域的研究重点和难点。目前,常用的基于数据驱动的径流预测方法有线性预测模型和机器学习模型。线性预测模型基于线性回归理论,结构简单,难以应对复杂非平稳的径流信息[1]。机器学习的发展为复杂径流的预测提供了新思路,其中传统浅层的机器学习方法虽然能够成功进行复杂非平稳的径流预测,但其精度仍需进一步改进[2]。随着人工智能技术的不断发展,深度学习被引入预测领域。其中长短期记忆(LSTM)模型具有较强的非线性预测能力、较快的收敛速度和捕捉时间序列长期相关性的能力,是一种具有特殊门控设计的循环神经网络(RNN),可以长时间保留历史有用信息[3],已有研究[4-5]证明了其在径流预测中的优势。虽然机器学习模型在水文预报领域已经取得了丰硕成果,但传统单一的神经网络模型学习过程易产生局部最优和过拟合问题[6]。为解决此问题,一些学者采用自适应调节人工蚁群(ARACS)、灰狼优化算法(GWO)、PSO 等算法优化神经网络参数,如白继中等[7]提出的自适应调节人工蚁群-径向基函数神经网络混合预测模型(ARACS-RBF),径流预测效果明显优于RBF 模型;王立辉等[8]提出灰狼优化的长短期记忆模型(GWO-LSTM),将其应用于径流预测,结果表明泛化性能较好;郑恺原等[9]提出的粒子群算法-加权随机森林模型(PSO-WRF),与WRF 模型相比,PSOWRF 模型优化效果显著,具有良好的预测精度和泛化能力。
由于径流序列高度的非线性与非稳定性,使得运用单一模型对径流序列进行预测,难以完全捕捉径流序列中的非线性因素。利用适当的时频信号分解技术分解原始水文时间序列建立集成模型,可有效提取水文时间序列中的有效信息,提高时间序列的平稳性和可预报性,从而提高模型的预报精度。许多学者对“分解-预测-重构”的组合预测模型进行了大量研究。周婷等[10]提出了小波分解-支持向量机-PSO 算法(WD-SVM-PSO)混合预测模型,基于淮河流域响洪甸水库1959—2014 年径流过程进行年径流预测,验证了时间序列分解预处理的有效性;孙娜等[11]提出了一种将EEMD、样本熵(SE)和正则化极限学习机(RELM)相结合的非平稳日径流预测方法(ES-RELM),基于金沙江下游控制站屏山站2000—2010 年的日径流实测数据进行日径流预测,表明分解后的模型预测精度更高;王文川等[12]采用具有自适应序列特征的时变滤波经验模态分解(TVF-EMD)与LSTM 耦合,构成TVF-EMD-LSTM 预测模型进行洛河流域长水水文站月径流预测;黄景光等[13]提出一种小波分析-支持向量机(WD-SVM)特征分类组合预测模型,基于宜昌站2013—2017 年日径流序列进行预测,结果表明相对于单一模型,新模型预测精度和稳定性明显提高;He 等[14]建立了变分模态分解(VMD)-深度神经网络(DNN)混合预测模型预报水库径流,预测性能优于EMD-DNN 和EEMD-DNN 等模型。小波分解需要根据经验预先设定母波函数及分解层数,受人为影响大;EMD、EEMD则可根据时间序列的局部特征自适应将序列分解为一系列固有模态分量,与WT 相比更具有普适性,但是容易存在伪分量和模态混叠问题,制约了预测精度的提高;VMD 是一种自适应维纳滤波器组,相比EMD 的递归筛选模式,VMD 是一种完全非递归的变分模态分解,能减少伪分量和模态混叠,并具有比EMD 和EEMD 更好的噪声鲁棒性[15],是分解复杂非线性非平稳时间序列的一种有效手段。
从以上研究可以看出,目前径流预测研究多是单步预测,利用“分解-预测-重构”方法对日径流多步预测的研究并不多见,而考虑不同预见期的径流预测模型能够对流域的防洪减灾起到更好的预防警示作用。常用的多步预测方法包括递推多步预测和直接多步预测。递归多步预测通过单步预测模型多次迭代来实现,将存在误差的单步预测输出作为下一步预测的输入,因此,随着多步预测的推进,预测误差不断放大,且在滞后较大的动态非线性系统中误差更为显著。而直接多步预测,根据模型直接得到多步预测值,不存在误差传播的问题,预测精度较高。如Atiya 等[16]对比了递推多步预测和直接多步预测的预测效果,结果表明直接多步预测比递推多步预测的预测效果更好、精度更高。
综合以上各研究方法的优势,本文将VMD 分解方法与LSTM 结合,并基于PSO 算法优化LSTM 模型参数,进行不同预见期下的日径流直接多步预测研究。
1 研究方法
1.1 变分模态分解(VMD)
VMD 是一种自适应、非递归的变分模态信号分解方法,其自适应性体现在可以根据输入信号的特性确定所给序列的模态分解个数k,并匹配每种模态的最佳中心频率和有限带宽,以便平衡处理序列各部分存在的噪声[17]。VMD 的目标是将一个原始输入信号分解成一组离散的具有特殊稀疏性的子信号(模态),在保证分解序列各模态的带宽之和最小的前提下,所有模态之和与原始输入信号相等,对模态函数进行希尔伯特(Hilbert)变换并进行变分约束,表达式如下:
式中:{uk}和{wk}分别为原信号分解得到的所有模态及其中心频率的集合;t为时间变量; δ(t)为狄拉克函数;uk(t)为分解序列模态调幅调频(AM-FM)信号;f为径流序列;是uk(t)的希尔伯特变换结果。
对式(1)进行重构,同时引入拉格朗日系数,转化为非约束变分问题,扩展的拉格朗日表达式为:
式中: λ为拉格朗日乘子; α为惩罚因子。将上述拉格朗日函数进行时-频域变换,并进行相应的极值求解,即可得到模态分量uk及中心频率wk的频域表达式:
式中:(w)相当于当前剩余量的维纳滤波;为当前模态函数功率谱的重心,对(w)进行傅里叶逆变换,实部则为uk(t)。最后,在迭代子优化序列中运用乘子交替方向法(ADMM),不断更新和wk得到最优解,进而求解分解层数k与各模态分量。
1.2 长短期记忆网络(LSTM)
LSTM 神经网络是一种特殊的RNN 网络,LSTM 通过其独特的门控设计,克服了传统RNN 学习长期依赖关系的问题,适合于处理和预测时间序列中间隔和延迟非常长的重要事件[18]。在原始RNN 中,只有一种内部状态ht,对于短期序列的输入比较敏感,LSTM 的循环单元更为复杂,与RNN 简单的tanh 层相比,其拥有4 个相互交替的网络层,如图1 所示。

图1 LSTM 网络结构Fig. 1 LSTM network structure diagram
LSTM 每一个循环单元都有一个新增的单元状态C,将前期输入信息长期保留,这是LSTM 更适用于长期序列的原因。在t时刻,网络的输入包括t-1 时刻的输出值ht-1、t时刻的输入值及t-1 时刻的单元状态Ct-1;网络的输出包括t时刻的单元状态Ct和输出值ht。
LSTM 的关键是对长期状态C的控制,LSTM 的神经网络模块使用了一种“门”(gate)结构,包括:输入门、遗忘门和输出门。输入门可将前序单元的信息输入到长期状态C中长期保留;遗忘门控制前一状态Ct-1中被遗忘的元素;输出门控制长期状态C在t时刻LSTM 模块中的输出。
1.2.1 遗 忘 门 遗忘门ft通过读取上一时刻输出值ht−1及当前时刻输入值xt,输出0 到1 之间的数值用于决定上一时刻单元状态Ct−1中信息保留比重。1 表示完全保留,0 表示完全舍弃。计算式如下:
式中:ft为遗忘门的输出;σ为sigmoid 函数;Wf为遗忘门的权重;ht−1为上一时刻输出值;xt为当前时刻输入值;bf为遗忘门的偏置项。
1.2.2 输 入 门 输入门it确定了当前输入的单元状态中用于更新当前时间步的最终单元状态Ct的信息。其中,是由上一时刻输出ht−1和当前时刻输入xt计算得出的当前输入下的单元状态信息,Ct取值范围为(−1,1),it取值范围为(0,1),计算式如下:
式中:it为输入门的输出;Wi为输入门的权重矩阵;bi为输入门的偏置项;Wc˜为单元状态的权重矩阵;bc˜为单元状态C˜t的偏置项;Ct为当前时刻的单元状态;Ct−1为上一时刻的单元状态。
1.2.3 输 出 门 输出门ot决定了Ct中用于作为当前时刻输出ht的信息。Ct经过tanh 层处理,得到(−1,1)之间的值。ot和ht的计算式如下:
式中:ot为输出门的输出;Wo为输出门的权重矩阵;bo为输出门的偏置项;ht为当前时刻输出值。
另外,本文采用PSO 算法优化LSTM 模型中隐含层节点数和学习率两个参数。PSO 是一种群体协作的随机搜索算法,通过不断迭代计算,协调粒子自身和群体的最优值对粒子当前运动方向和运动速度的影响,全局极值不断更新来找出问题的最优解。具体原理见文献[19],这里不再赘述。
1.3 VMD-PSO-LSTM 径流预测模型
VMD-PSO-LSTM 径流预测模型综合了VMD 分解方法自适应、完全非递归的特性及PSO-LSTM 神经网络参数自动寻优、长期数据记忆的优势。模型的建立包含以下4 个步骤:
步骤1:VMD 序列分解。使用VMD 算法将原始径流序列分解成k个离散的固有模态分量(SIMF),使非平稳原序列分解得到多个较稳定的子序列。VMD 分解效率和预测精度主要受分解层数k和惩罚因子等参数的影响,VMD 分解虽具有较好的分解效果,但存在确定分解层数k的不确定性问题,因此本文采用排列熵优化算法(permutation entroy optimization,PEO)实现分解层数k的自适应确定。该算法具体步骤参考相关文献[20]。
步骤2:PSO 参数优化。利用PSO 算法对LSTM 网络的参数进行优化,使得网络隐含层节点数(NHN)和学习率(α)达到最优。
步骤3:LSTM 网络训练。在参数优化的基础上建立预测模型,使用步骤2 得到的最优参数建立LSTM 网络,对每个子序列进行LSTM 网络训练。在训练之前需将分解后的各SIMF进行归一化处理(由于径流序列具有高度非线性和非平稳性,因此必须对输入数据进行归一化处理,以避免训练过程中数据出现大的波动)。
其中,直接多步预测在模型中以滑动窗口机制实现,假定一段径流时间序列为X=[x1,x2,…,xn],模型输入步长为L,即滑动窗口的当前窗口长度为L;滑动窗口的移动步长为1;当预测预见期为a(本文预见期设为1、2、3 d)时,当前t时刻向后预测a天的直接多步预测模型输入输出结构如图2 所示。

图2 直接多步预测示意Fig. 2 Schematic diagram of direct multi-step prediction
步骤4:序列预测。利用PACF 偏自相关分析法确定的输入变量,在训练好的LSTM 网络的基础上对每个子序列进行预测,各SIMF预测值叠加即为最终预测结果。
2 实例分析
本文采用黄河下游花园口和利津站2003—2012 年的逐日径流资料作为研究数据(数据均来源于黄河水利委员会),以2003—2009 年的日径流序列为训练数据,2010—2012 年的日径流序列为验证数据。花园口和利津站的日径流序列过程见图3。

图3 花园口和利津站的日径流序列Fig. 3 The daily runoff sequence at Huayuankou and Lijin Stations
VMD 分解方法具有自适应性和强大的降噪性能,针对径流序列的非平稳性,将频率不同且成分复杂的径流时间序列分解成具有固有模态函数的平稳性序列分量SIMF,采用VMD 法分别对花园口和利津站的日径流序列进行分解,经过排列熵算法,自适应得到最优k值,从而获取k个序列分量。花园口和利津站的日径流序列经分解得到的子序列个数分别为6 和8 个。参考相关文献[15,21],本文模型惩罚因子取2 000。以花园口站为例,研究数据的分解结果如图4 所示,可以看出,通过VMD 分解,将原始日径流序列分为了由高频到低频的周期性模态分量与表示趋势的残差,揭示出日径流数据内的隐藏信息,即周期性震荡变化和趋势。这样不仅使模型能更好地理解周期性的信息,同时也有利于提高模型的训练和预测精度。
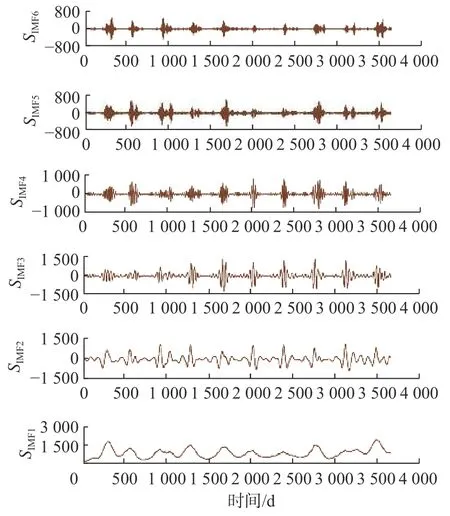
图4 花园口站VMD 分解各分量结果Fig. 4 VMD decomposition results of each component at Huayuankou Station
对于上述每个SIMF分别建立PSO-LSTM 预测模型,各子序列预测结果的叠加即原径流序列的预测结果。其中模型的输入步长利用偏自相关函数(PACF)来确定,可突出时间滞后对当前时段径流的影响。假设输出变量为xi,当滞后L的偏自相关系数fPACF超出95%置信区间时,前L个变量即为输入变量[22]。以花园口站为例,原始日径流序列经过VMD 分解得到6 个子序列,由PACF 计算得到各SIMF的输入步长分别为1、6、4、4、8、11,如图5。具体的输入步长及输入变量如表1 所示。LSTM 网络隐含层节点数(NHN)和学习率(α)利用PSO 算法确定,隐含层数为2 层。以花园口站为例,每个SIMF在1~3 d 预见期对应的最优NHN和α值见表2。模型的输入层节点数等于输入变量数,输出层节点数为1。将当前时段t之前的数据作为模型的输入,分别将t时刻、t+1 时刻、t+2 时刻的预测数据作为输出构建预测模型,实现预见期1~3 d 的多步预测。

表1 花园口和利津站各SIMF 的输入步长及输入变量Tab. 1 Input steps and input variables of each SIMF at Huayuankou and Lijin Stations

表2 花园口站各SIMF 对应隐含层节点数(NHN)和学习率(α)Tab. 2 The number of hidden layer nodes (NHN) and learning rate (α) corresponding to SIMF at Huayuankou Station

图5 花园口站各子序列的fPACFFig. 5 PACF method input step recognition of sub-sequence at Huayuankou Station
3 结果分析
基于VMD 的分解结果,根据输入步长,将t时刻之前的数据作为输入变量,构建每个SIMF的PL 模型,将t时刻、t+1 时刻、t+2 时刻的数据作为输出结果,分别将各子序列的预测结果进行加和,实现1~3 d 的VPL 多步预测。为了进一步验证VPL 模型在径流多步预测中的优越性,建立PSO-LSTM(PL)、CEEMDPSO-LSTM(CPL)多步预测模型进行对比。建模所用的训练数据和验证数据同VPL 模型。其中,日径流经CEEMD 分解,花园口得到13 个子序列,利津12 个子序列,比VMD 分解的子序列个数分别多了7 和4 个。VPL模型、CPL 模型和PL 模型的预测结果评价指标见表3。

表3 不同模型的预测结果对比Tab. 3 Comparison of prediction results of different models
对比VPL 模型、CPL 模型和PL 模型的预测结果指标可知,总体上3 种模型的预测精度:VPL 模型>CPL 模型>PL 模型。在验证期,VPL 模型的预测精度最高,在1~3 d 预见期下,其ENS、ERMS、R基本上均优于其他两种模型。另外,经过分解后的VPL、CPL 组合模型预测精度明显优于未经分解的PL 模型,在1~3 d 预见期下,VPL 模型对PL 模型各指标的改进效果比CPL 模型更为显著。随着预见期增长,分解后模型各个指标的改进效果更显著。
在1~3 d 的预见期下,VPL 模型比CPL 模型的ENS提高了5.1%、9.3%、2.6%,ERMS降低了29.4%、32.6%、10.1%,R值提高了2.7%、1.8%、0.3%,可能的原因是VMD 通过自适应k值,减少了子序列的个数,从而减少了子序列预测结果叠加过程中产生的累计误差。随着预见期的增长,VPL 和CPL 模型的预测精度都出现了降低的趋势,以花园口站为例,VPL 模型在1~3 d 的预见期下,ENS能够保持0.9 以上,而CPL 已经下降到0.854。这表明VPL 模型保证了预见期增长时预测精度的稳定性。
以花园口站为例,VPL 模型、CPL 模型、PL 模型的预测径流过程和散点图如图6 所示。从径流过程对比图可以看出,VPL 模型的预测径流过程最接近实测径流过程,且VPL 模型的峰值预测精度要明显优于CPL、PL 模型,虽然随着预见期的增长,3 种模型的预测峰值在时间和大小上与实测值相比都有了不同程度的偏移,但是VPL 模型的预测峰值的偏移程度相对微弱。由散点图可知VPL 模型在1~3 d 预见期下的R2值比CPL、PL 模型更高,预测结果更加接近实测径流,尤其是中高流量,VPL 预测结果散点图相对CPL、PL 模型更加集中于45°线,说明VPL 模型对中高流量的预测精度较好。

图6 花园口站2010 年不同预见期各模型预测结果与实测值的比较Fig. 6 Comparison of the predicted results and measured values of Huayuankou Station in different forecast periods in 2010
综合以上分析,与CPL、PL 模型预测结果相比,在预见期为1~3 d 的情况下,VPL 模型均表现出更稳定、更精确的优势,实现了高精度的日径流多步预测。
4 结 语
针对日径流时间序列的强非线性和非平稳性,本文提出了VMD-PSO-LSTM 混合多步预测模型。为了验证该混合模型在日径流多步预测中的适用性,对黄河下游花园口和利津站进行了预见期1~3 d 的多步预测,与PSO-LSTM、CEEMD-PSO-LSTM 模型预测结果对比,得出以下结论:
(1)与未分解模型相比,“分解-预测-重构”模式的组合预测模型的预测精度明显提高,且随着预见期增长,分解后模型的优势更加显著。可见信号分解方法有助于预测模型更好地学习径流序列中的周期、趋势等本质特征,提高日径流的预测精度。
(2)与其他分解方法相比,VMD 方法更能有效提取日径流序列的特征信息,减弱原始日径流序列的非平稳性,进而得到更优的预测结果。因此该分解方法的频率分离性能更佳,对噪声干扰具有较好的鲁棒性,可以有效减少伪分量。
(3)VMD-PSO-LSTM 混合多步预测模型在预测精度、预测稳定性方面展示出独特优势,尤其对中、高值流量预报表现出较强的跟踪预报能力,为实现复杂非平稳日径流时间序列的高精度多步预测提供了一种新途径。
——花园口电灌站的郑州记忆

