混凝土坝变形监测时序中异常突变值的优化诊断

陈良捷，魏博文，戴国强，林太清

(1. 江西省水利科学院，江西 南昌 330029； 2. 南昌大学 工程建设学院，江西 南昌 330031)

大坝安全监测是融合水工结构学、仪器仪表学、计算统计学和网络技术的“医院”系统，广泛应用于大坝等水工建筑物的服役环境、变形效应、渗流效应、应力应变等数值量测[1-3]。原型监测时序主要来源于监测仪器对建筑物固定测点进行一定频次的自动化或人工观测。混凝土坝监测项目主要分为5 类：环境监测、变形监测、渗流监测、应力应变监测、专项特殊监测，其中变形监测时序是坝体结构在多元复杂环境共同驱动下产生变形效应的直接表现，是混凝土坝服役健康诊断的重要基础[4-5]。近年来，随着计算机技术的发展及筑坝监测硬件配置完备性的提高，大坝数据采集方式愈加多样化、自动化，存储机制与规模也逐步成熟庞大[6]。但由于设备更替修缮及人为管理疏漏等不确定因素，监测时序中难免出现异常、空缺等现象，对海量数据集进行科学高效的可靠性辨识及预处理是构建大坝安全监控体系的关键首步[7-10]。

国内外学者针对大坝安全监测数据集的可靠性辨识及异常突变识别技术方面展开了研究。郑霞忠等[11]基于环境自变量与效应因变量的关联性约束机制提高了监测异常数据清洗的准确性，通过密度聚类算法识别时序中离群孤立点集，并依据关联信号清洗规则有效辨识粗差部分，借助粒子群优化的最小二乘支持向量机模型补齐数值空缺；西班牙学者Salazar 等[12]基于强化回归树模型计算结果与实际观测之间的差异判断疑似异常效应序列，并辅以温度场及静力场耦合的有限元仿真验证其可靠性，有效规避了因异常载荷而导致的虚假异常现象；王丽蓉等[13]将大坝原始监测时序绘制成数据过程线图，基于卷积神经网络自主解析图像特征的能力优势，识别序列点集的异常离群类型并搜寻具体位置；郑东健等[14]为保护观测资料样本整体性并准确反映异常干扰对各效应分量的局部影响，构建了指示变量数值模型以有效模拟各种系统干扰的影响量值。但是，目前现有的研究方案及成果未将效应监测时序的自身结构特性融入其中，致使复杂混频信号的内部交互干扰成为异常突变识别工作的障碍。因此，如何开展科学可靠的监测数据可靠性辨识及预处理工作亟需更深层次的研究分析。

针对混凝土重力坝变形监测时序中异常突变值的识别难题，本文依据经验小波变换理论提取序列信号极大值点并自适应地分割傅里叶频谱，通过构造正交小波滤波器组获取信号的不同模态，进而排除监测时序中趋势分量对异常突变诊断工作的干扰；以待测数据对象周围领域的局部数据分布密度为检测指标，重点识别局部异常因子远大于1 的数据点，最后将计算结果通过统计箱形图精准找到对应的数据序号以便剔除。

1 混凝土坝变形监测时序的内部信息特征

混凝土坝变形规律的复杂性导致其内在的多元映射关系难以准确描述，通常基于长时间的监测数据建立回归模型[15-16]，根据各环境因子对因变量作用的显著程度，从大到小依次逐个引入方程式，最大限度展示变形效应的驱动来源。由于现场监测技术的局限性及各类环境影响的强度差异，混凝土坝变形按照经典分析理论可分为3 个部分：水压分量 δH、温度分量 δT和时效分量 δθ[17]，以混凝土重力坝为例，其拟合公式可表示为：

式中：H为水深；an为回归模型水压分量的拟合系数；b1i和b2i为回归模型温度分量的拟合系数；i为时间周期，i=1表示年周期，i=2表示半年周期；t为从建模资料序列到始测日的累计天数，t0为从建模资料序列的第1 天到始测日的累计天数；c1和c2为回归模型时效分量的拟合系数；θ=t/100。

但是，现场观测的项目种类有限且经典统计模型产生的残差序列 δR较大，无法解释结构变形效应的全部因果关系，混凝土坝变形时序中各个组成分量大体趋势如图1 所示。从图1 可以看出，水压分量 δH、温度分量 δT和时效分量δθ的趋势曲线较为平稳，而残差序列 δR表现出强非线性、高频率的不稳定特征。因此，构建混凝土坝变形监测时序异常点诊疗体系的关键首步是解译混频信号的复杂多元内部信息。

图1 变形监测数据各组成序列的近似趋势Fig. 1 Approximate trend of each component sequence of the displacement monitoring data

2 基于EWT-LOF-BOXPLOT 的异常突变值诊断方案

2.1 经验小波变换

经验小波变换（Empirical Wavelet Transform, EWT）[18-19]是一种新型多分量信号处理方法，其主要思想是基于傅里叶支撑选择1 组正交小波滤波器组，其中包括1 个低通滤波器和N−1个带通滤波器，分别对应趋势分量和细节分量，随后对调幅-调频模态进行希尔伯特变换，以获取信号的瞬时频率和瞬时幅值。该方法充分融合了小波变换（Wavelet Transform, WT）和经验模态分解（Empirical Mode Decomposition, EMD）的优势，适合处理非线性、非平稳特性数据的分解难题[20-21]。

假设大坝原型变形监测信号 δ(t)表达式为：

式中：δn(t)为调幅-调频信号；An(t)为调幅部分函数；Fn(t)为调频部分函数。为完全自适应分割监测信号 δ(t)的频谱，将傅里叶支撑区间[0, π]划分为N个连续部分，即：

式中： ∆i为不同子体部分，i=1,2,···,N； θi为不同子体部分的区间边界，θ0=0且θN=π。设定以 θi为中心，宽度为2 ρ的过渡区间，为每个子体部分 ∆i构造以Meyer 小波函数为基础的经验小波带通滤波器。经验小波函数和经验尺度函数表达式为：

式中：λ(x)为区间[0, 1]内满足K阶导的任意函数； ρi为过渡阶段的宽度参数。两者表达式分别为：

信号 δ(t)与经验小波函数fi(θ)的内积为细节系数C(i,t)，信号 δ(t)与经验尺度函数g1(θ)的内积为趋势系数C(0,t)，具体表达式为：

式中：IFFT−1()为快速傅里叶逆变换；fˆi(θ)和gˆ1(θ)分别为fi(θ)和g1(θ)的傅里叶变换；fi(θ)和g1(θ)分别为fi(θ)和g1(θ)的共轭复数。结合式（2）和（8），原信号的重构表达式及单分量经验模态分别为：

式中： ∗为卷积运算；Cˆ(0,t)和Cˆ(i,t)分别为C(0,t)和C(i,t)的傅里叶变换形式。原始真实信号通过EWT 方法可自适应地分解成许多具有紧凑支持频谱的经验模态函数。

2.2 局部异常因子

局部异常因子（Local Outlier Factor, LOF）检测方法是Breunig 等[22]于2000 年提出的基于密度的无监督离群点识别工具。其主要手段是通过比较待测数据点与其领域数据点的聚集密度，以此密度比值为依据判断该待测数据点是否为离群异常点。相比其他基于距离、统计分布的检测方法，LOF 仅考虑待测数据对象周围领域的局部数据分布，可避免其他领域外数据集的干扰[23-25]。

假设存在由j个i维数据点组成的样本集合S，从中任意取两个样本点M=(xm1,xm2,···,xmi)与N=(xn1,xn2,···,xni)，其中m和n皆取自[1,j]，则两点之间的欧几里得距离表达式为：

定义Dk(M)为数据点M的第k距离，若Dk(M)=D(M,N)，则数据点N是指在样本集合S中除了数据点M之外距离数据点M最近的第k个点。假设Ek(M)为数据点M的第k距离邻域，则其表达式为：

由式（12）可知，数据点M的第k距离邻域Ek(M)是指在样本集合S中除了数据点M之外的所有距离数据点M小于或等于数据点M的第k距离Dk(M)的数据点集合，相关示意图如图2 所示。

Mk图2 数据点 的第距离邻域示意Fig. 2 The distance neighborhood diagram of data point k M

定义Dk(M,L)为数据点L与数据点M之间的第k可达距离，其实际意义是指当数据点L位于数据点M的第k距离邻域内时，Dk(M,L)只能等于数据点M的第k距离Dk(M)。当数据点L位于数据点M的第k距离邻域外时，Dk(M,L)为两点之间的欧几里得距离D(M,L)，数学表达式为：

设定ρk(M)为数据点M的局部可达密度，可理解为在数据点M的第k距离邻域Ek(M)中除了数据点M外的所有点与数据点M之间的平均第k可达距离的倒数，表达式为：

由此可得在数据点M的第k距离邻域Ek(M)中除了数据点M外所有点的局部可达密度，将其分别与数据点M自身局部可达密度的比值叠加求平均，即得数据点M的局部异常因子，其表达式为：

若Lk(M)值接近1，则数据点M的第k距离邻域Ek(M)内的数据点的密度相差不大，数据点M与其邻域内其他数据点属于同簇；若Lk(M)值远小于1，则数据点M的密度比其邻域内其他数据点的密度大，数据点M可被判定为密集点；若Lk(M)值远大于1，则数据点M的密度比其邻域内其他数据点的密度小，数据点M可被判定为异常点。

2.3 离群点检测模型的建成方案

混凝土重力坝长期深处于静力场和温度场中，其变形效应也备受水压、温度等周期性影响，因此变形监测数据存在一定的趋势分量，对LOF 异常点检测工作产生较大影响。为了确保检测模型的精准运行，采用EWT 信号处理方法对原型监测数据进行分解，去除变形监测时序的运行趋势。异常值属于短时突变值，用此检测方案不但不会遗漏任何离群点信息，还有利于消除多变工况对异常数据点检测的影响，提高离群点检测模型的可靠性。

为了进一步精准确定数据点SLOF的判断阈值，且避免人为设定带来的诸多不确定因素，本方案采取可反映数据点分散情况的箱形图。箱形图于1977 年由美国统计学家John Tukey 发明，能显示出一组数据的最大值、最小值、中位数及上下四分位数，既不需要对待检数据进行服从特定分布的事先假定操作，也没有任何限制性要求，可真实直观地表现数据形状的原生面貌。

根据处理多种数据试算经验，箱形图已经定义了异常值识别标准：

式中： δ′′为待检数据的异常值；Qu和Qd分别为待检数据的上下四分位数；sIQR为待检数据的四分位距，即sIQR=Qu−Qd。箱形图对数据集异常值的识别标准是基于具有一定耐抗性的四分位数和四分位距，避免了异常值对自身产生的扰动影响，增强了整体模型的稳定性和准确性。

综上所述，混凝土重力坝变形监测时序的离群点检测优化模型建成方案如图3 所示。

图3 优化诊断方案流程Fig. 3 Flow chart of optimized diagnosis scheme

3 工程应用

某混凝土重力坝位于浙江省境内，最大坝高115 m，坝顶全长466.5 m，水库总库容2.2×1010m3。该混凝土坝设有变形、渗流、应力应变、裂隙裂缝等监测项目，其中位移监测主要有正垂线（PL）、倒垂线（IP）、坝顶引张线（EX）及多点位移计（M）等，其位移监测系统布置如图4 所示。

图4 大坝位移监测系统布置示意（单位：m）Fig. 4 Schematic layout of dam displacement monitoring system (unit: m)

本文选取该混凝土坝第4 号坝段115 m 高程处的水平位移自动化监测时序 δ115为研究对象，其时间区间为1998 年4 月20 日至2018 年4 月30 日，并规定以向下游方向位移为正，向上游方向位移为负。由于该混凝土坝监测系统更新改造过数次且管理方案有改变，致使其时间序列步长各不相等且无规律可寻，经整理后得其序列数据容量为757 组。

由于大坝在运行期间会受到库水位、温度等工况变化且离群异常点具有短时突变特性，故大部分隐藏于数据集的高频区间段内。因此在对该混凝土重力坝位移监测时序进行LOF 异常点检测之前，需利用EWT 信号处理方法去除监测时序的趋势分量，将分解出的趋势分量与原始数据进行对比，结果见图5。

图5 趋势分量与原始数据对比Fig. 5 Comparison between trend component and original data

由图5 可知，大部分数据点位于监测时序的趋势曲线上。通过整理得757 组水平位移序列的平均值为0.475 mm，最大值为5.270 mm，最小值为−4.800 mm，区间跨度较大，且存在个别疑似异常值。

在通过EWT 信号处理方法对该位移监测时序进行分解处理后，人工剔除蕴藏于原始信号中的趋势分量，对应每个数据序号重构剩余的高频分量，再对重构后的位移效应细节信号进行异常点检测以求出各数据点的SLOF，结果如图6 所示。

图6 LOF 异常点检测结果Fig. 6 The detection result diagram of abnormal points

由图6 可知，基于大坝位移时序细节信号计算出的SLOF大多数位于1 附近，说明大多数据点第k距离邻域内的数据密度相差不大，即这些数据点与其邻域内其他数据点属于同簇。通过整理计算，该细节信号序列SLOF平均值为2.057，最大值为8.563，最小值为0.783，中位数为1.604，下四分位数（25%）为1.059，上四分位数（75%）为2.685。现将其LOF 数据集作箱形图以寻找异常值，其结果如图7 所示。

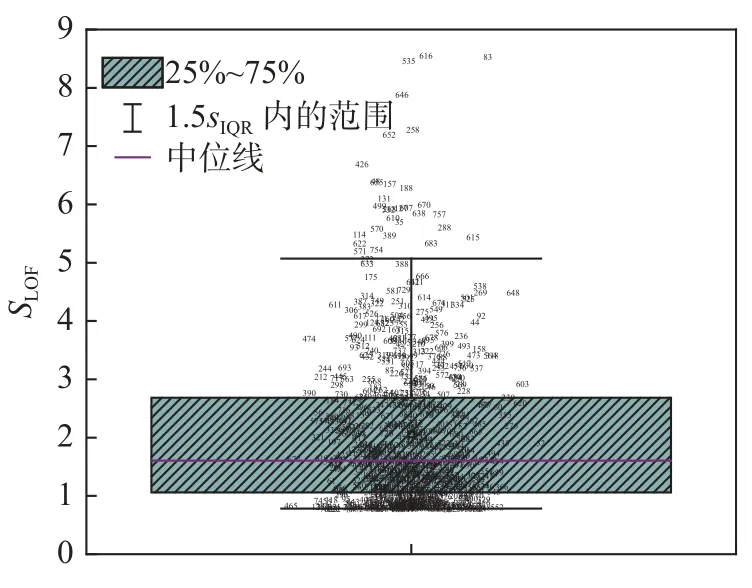
图7 箱形图检测结果及异常值对应的序号位置Fig. 7 Boxplot results and number positions for exceptions

在箱形图7 中，上下两条末端横线并非准确的1.5 倍箱子长度，而是不超过该长度的最远值，即表示该批数据正常值的分布区间。根据箱形图7 显示的数据序号可对原始数据进行对应剔除，得出异常突变值共32 组，优化处理后得监测数据725 组。

为了验证该基于EWT-LOF-BOXPLOT 的异常突变值诊断方案对监测数据集优化的有效性和实用性，将优化前后及单一LOF 方法检测处理的数据分别代入经典多元回归模型中参与计算，得到的模型误差拟合结果如图8 所示；并引入统计学领域中衡量计算精准度的评判指标：平均绝对误差EMA、均方误差EMS、平均绝对百分误差EMAP及决定系数R2，计算结果如表1 所示。

表1 计算精度的评判指标Tab. 1 Evaluation index of calculation accuracy

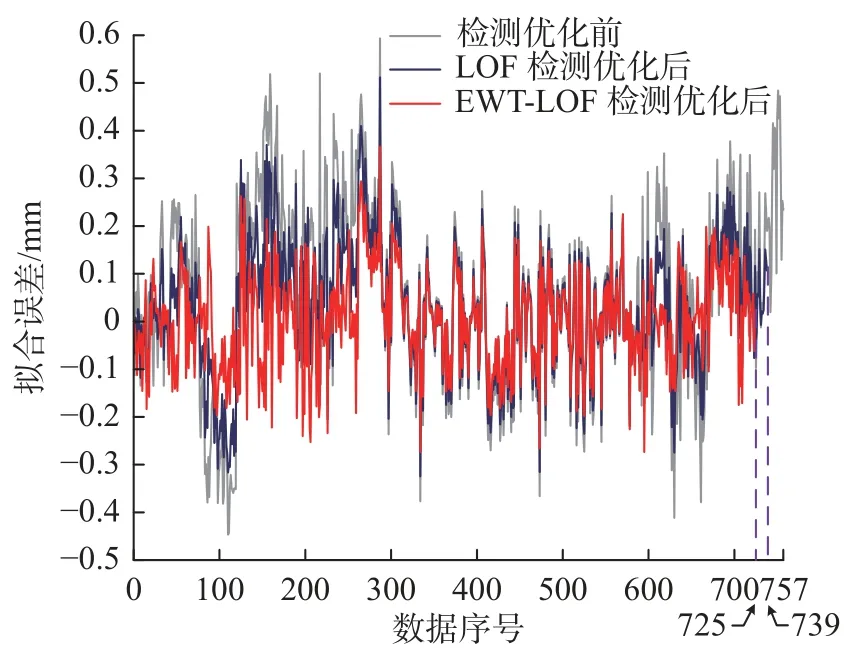
图8 优化前后的数据拟合结果Fig. 8 Data fitting results before and after optimization

综合对比图8 与表1 可见，通过经验小波变换去除监测时序的运行趋势，使样本数据集的LOF 识别检测更加精确，提高异常突变值的诊断效力；监测样本数据集经过基于EWT-LOF-BOXPLOT 的异常突变值诊断方案优化后，参与回归拟合计算的平均绝对误差、均方误差、平均绝对百分误差皆小于优化前及单一LOF 检测识别，且R2值更接近于1，这表明该方案优化处理后的混凝土坝变形监测时序更适用于回归建模，有助于后续研究的监控模型建立及反演反馈分析。

4 结 语

（1）混凝土坝变形时序因监测设备更新改造或人为管理疏漏等不确定因素而产生异常突变点值，为提高原型观测数据的真实性及计算可靠性，提出了一种针对混凝土坝变形监测时序中异常突变值的优化诊断方案。

（2）考虑到变形监测时序是由多元环境组合驱动的综合表现，其内部信息特征复杂且存有多频信号干扰，采用经验小波变换理论和箱形图统计手段对局部异常因子计算模式进行优化，有效规避了单一检测模型在进行离群点识别时的判诊局限。

（3）工程实例分析表明，相比于经典局部异常因子计算机制，本文提出的异常点诊疗体系的检测能力更优，且建模方法简便高效，加以修改可推广应用于大坝其他监测效应时序的优化诊断。但是，由于本方案是基于效应样本数据集进行自体内部运算，未引入周边环境资料的考证，故对具有调节性能的水库大坝存在一定局限性。