长江南京段河床与洲滩平面演变特征遥感分析
杨 志,董坤明,王 珊,陈 槐,王乃茹,范红霞
(1. 安徽省现代交通设计研究院有限责任公司,安徽 合肥 230011; 2. 水发规划设计有限公司,山东 济南 250100; 3. 江宁区水务局,江苏 南京 210000; 4. 南京水利科学研究院 水文水资源与水利工程科学国家重点实验室,江苏 南京 210029)
随着南京沿江经济的发展,对长江岸线、水资源开发利用的要求愈发迫切,对长江河势稳定、防洪安全的要求也越来越高。探讨南京河段的河床与洲滩演变特征,可为南京段河势稳定、岸线资源的开发利用等提供科学依据,具有重要的研究意义[1]。长江南京段是典型的分汊型河道,相关的河床演变研究较多,但受水文测站布点、地形资料等制约,研究往往只局限于局部河段[2]。臧英平等[3]根据监测资料分析了长江南京段近20 年5 个时期的河势及岸段变化,表明河势基本稳定,深泓线横向摆动较小,深槽区平面位置基本稳定,岸线冲淤变化不大;朱宇驰[4]利用长江南京段近50 年4 个时期的航道图,结合GIS、RS 和数字高程模型(DEM),分析了南京段的岸线变迁及水下地形冲淤演变,总体表现出淤积-冲刷-稳定的特征;徐韦等[5]利用1998 年和2013 年南京段的历史水下地形数据,结合2015—2016 年多波束测深、流速与河床沉积物数据,探讨了南京段河槽演变对三峡水库等人类活动的响应规律。
传统的河床演变分析很大程度上受制于水文站点和野外实测资料,仅利用传统观测手段很难全面有效地掌握河流基本信息。随着科学技术的发展,卫星遥感可获取多时相观测影像数据,能为河床演变提供直接有效的方法,越来越多的研究人员采用卫星遥感影像研究河床平面形态的变化[6-8]。河床平面形态的变化与河床演变关系密切,河床平面形态通过平面位置迁移、河宽变化、沙洲的形态变化及其产生和消亡过程、汊道增减等,来反映河床演变过程[9]。已有关于长江的卫星遥感研究成果极多,但极少针对南京河段的详细研究。严夏青等[10]提取了2016—2020 年月度长江干流上海至宜宾段水域面积,并分析其年际、年内变化规律;姜玲玲等[11]研究了长江干流江心洲在1984—2019 年的变化过程,发现江心洲在过去35 年平面形态总体上以扩张为主,但存在一定的区域性差异。
鉴于目前南京段长时间序列演变分析的研究成果较少,且遥感影像演变方面研究不足的现状,通过广泛收集南京河段长时间遥感影像序列(共约800 幅),并引入本征正交分解法分析河床边界和洲滩的时空精细演变特征,以期为河流的合理开发利用、科学保护和有效管理提供支撑。
1 研究区域及数据分析方法
长江南京段位于江苏省境内,上起猫子山,下至三江口,全长93 km,是长江中下游干流14 个重点河段之一(图1)。长江两岸干堤总长191.05 km(不含洲堤、以山代堤段和通江河港堤),其中江南97.72 km,江北93.33 km。径流下行受潮水上行顶托形成两种水势交互,在南京段形成了新生洲、新济洲、梅子洲及八卦等诸多沙岛和浅滩,使长江在南京段多次分汊,主、支汊交替变化。
1.1 数据来源
本文收集的数据主要来自Landsat(地球资源技术卫星),包括1984—2020 年间南京河段所属区域(Landsat 轨道号(120,38))约800 幅卫星遥感图片(卫星重现期为15 d,每月2 幅),仅利用其中两个波段(Green 绿、NIR 近红外)的数据,空间分辨率为30 m。南京潮位资料来源于历年的《长江流域水文资料》第6 卷第6 册。
1.2 计算方法
采用基于绿波段与近红外波段的归一化差分水体指数(NDWI)来凸显影像中的水边线信息[12]。以2020-02-06 的南京段遥感影像为例,经过归一化差分水体指数计算后,采用otsu 阈值分割算法进行二值化(图2(a))。可见,NDWI 指数可清晰凸显出水边线信息。图2 中黑色区域取值为0,白色区域取值为1。
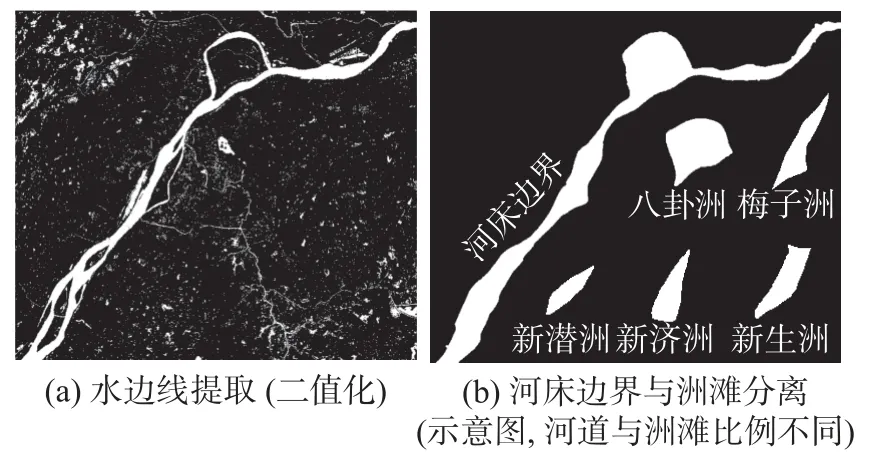
图2 长江南京河段河床边界与洲滩提取(2020-02-06 遥感影像)Fig. 2 The extracted shorelines and sandbars in the Nanjing reach of the Yangtze River
当水边线信息凸显后,采用形态学方法提取河床边界和洲滩,主要利用开操作与闭操作。利用形态学方法提取长江南京段河床边界和5 个大洲滩(图2(b))。为清晰显示,图2(b)中河床边界和洲滩的比例尺不同。由于Landsat 卫星影像分辨率为30 m,在提取河床边界和洲滩面积时会引发误差,本文按最不利情况考虑,即所有的水边线提取误差都为30 m。
本征正交分解法(Proper Orthogonal Decomposition,POD)主要对高维度特征数据进行降维,仅保留高维度数据最重要的特征,去除噪声和不重要的特征,从而简化数据分析。本文主要用于河床边界或洲滩形态序列中含能模态的提取。POD 方法将信号序列投影到最优函数空间,使信号在该最优函数空间投影的平均能量最大,则该最优函数空间的解为信号序列的空间相关系数矩阵的特征向量空间,可通过特征分解进行求解,具体步骤见文献[13]。
2 计算结果
2.1 遥感影像筛选
采用目视解译法人为挑选了289 张不受云层影响的遥感影像,分析可用遥感影像的时域分布特征。由图3 可见,夏季6—9 月降雨较多,云层覆盖频繁,导致可用图片数量较少;可用图片的年际分布也不均。水边线提取需要在同一水位(拟定为85 高程5 m 水位,接近南京河段造床流量45 000 m3/s 对应水位5.31m)下,南京河段岸坡坡比一般为1∶5,按Landsat 卫星图片30 m 的分辨率,小于6 m 的水位差反映在图片上不超过1 个像素;同理,五大洲滩的坡比一般为1∶13,只要水位差小于2.3 m,则误差不超过1 个像素。以2015 年为例,图4 给出了南京潮位站的日均水位,从2015 年可用遥感影像中筛选出4 月和10 月各1 张可用照片,其拍摄日期的水位与拟定5 m 水位差为±1 m,满足河道及洲滩的水边线提取要求。同理,从每年图片中选取2 幅组成新的序列,共74 幅,其中最大的水位差为2 m,满足计算精度要求。

图3 可用遥感影像的时域分布特征(总数289)Fig. 3 Temporal distribution characteristics of available remote sensing images (total 289)

图4 2015 年南京潮水位站日均水位(以水位5 m±1 m 筛选遥感影像)Fig. 4 Daily average water level at Nanjing tidal level station in 2015 (filtering at water level 5 m±1 m)
图5 为最终筛选出的历年遥感影像拍摄时间。1984—2020 年,筛选的影像时间基本分布在每年的3—4 月和10—11 月,只有极个别年份的可用影像拍摄时间在2、7 和12 月。
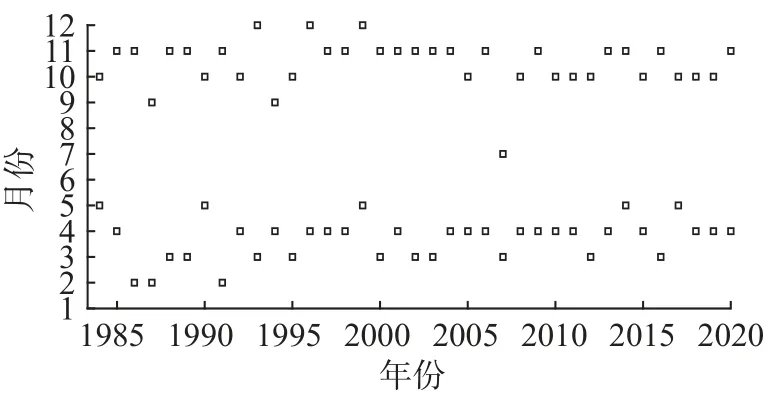
图5 筛选出的遥感影像(总数74,每年2 幅)Fig. 5 Filtered remote-sensing images (total 74, two images per year)
2.2 河床平面演变特征
图6 给出了近40 年南京段河道水面面积随时间变化情况,河道面积提取相对误差均值为2.0%。图中的水面面积指南京河段河床边界包围的区域,包括了洲滩面积。近40 年来,南京河段的水面面积缓慢下降,从最大的340 km2下降至320 km2,减幅约为6%。说明人类活动不断侵蚀河流,使河床边界向内收缩。
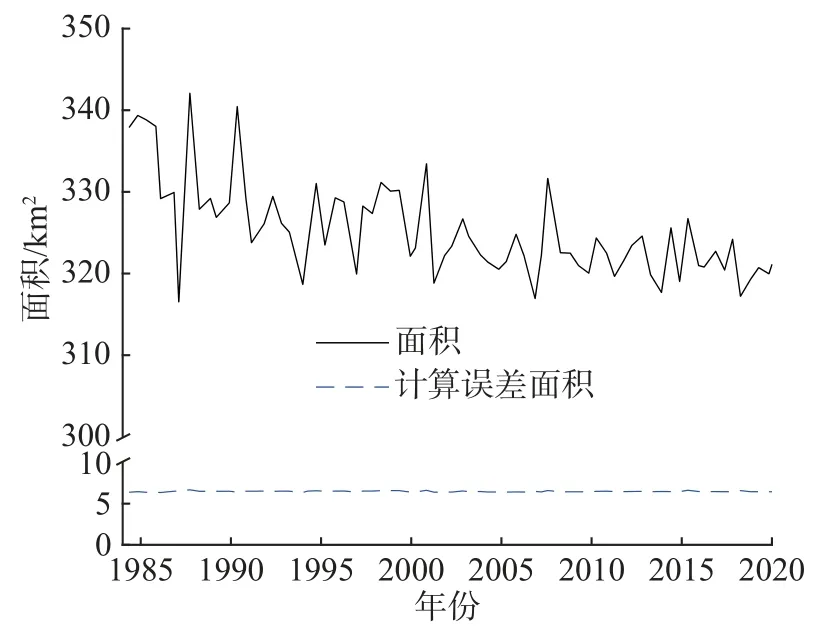
图6 南京河段水域面积随时间变化(相对误差均值2.0%)Fig. 6 Temporal variation of mainstream area in the Nanjing reach in recent 40 years
图7 为南京河段河床边界的均值和方差。近40 年来,猫子山对岸、南京青奥体育公园、太子山公园及长江村附近的河床边界出现了较大改变,尤以长江村的河床边界变化最为剧烈,减小面积约10.35 km2,占近40 年总变化面积的52%,主要由水产养殖和围河造田导致。
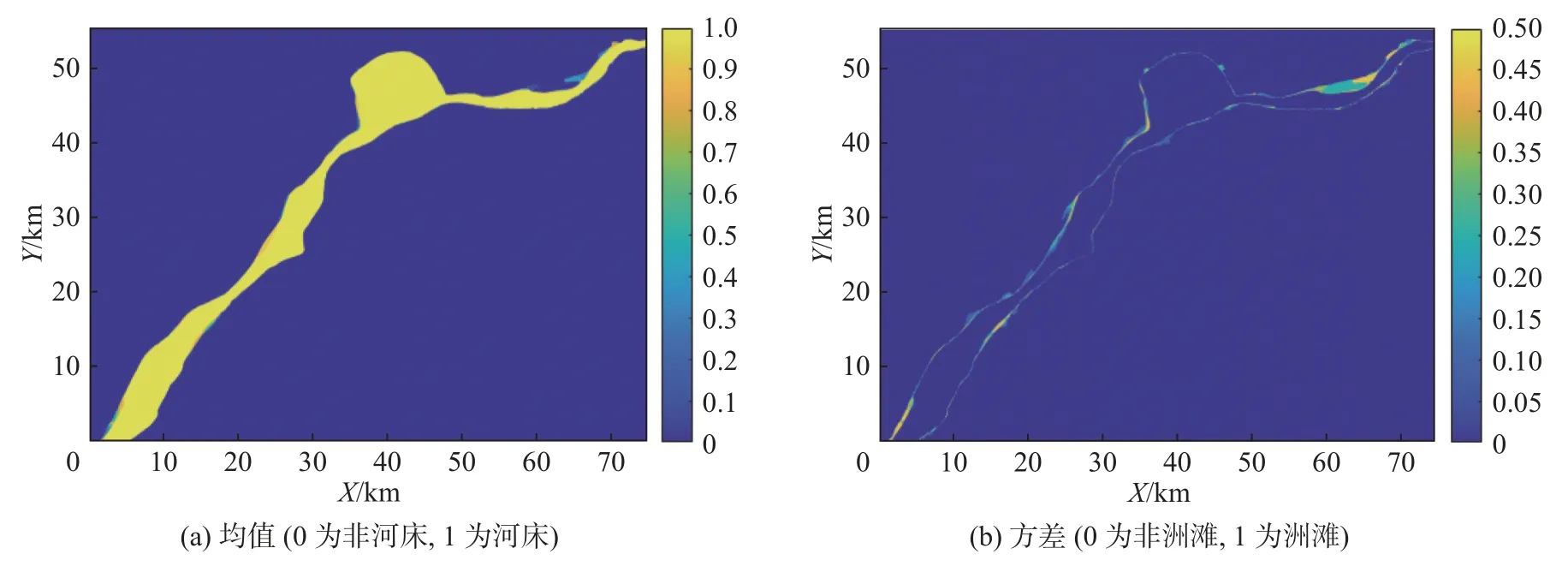
图7 近40 年南京河段河床边界统计参数Fig. 7 Statistical parameters of the river boundary sequence of the Nanjing reach in last 40 years
利用本征正交分解法提取了南京河段河床边界序列的主要含能模态。由图8 可知,一阶模态含能比例很高(97%),贡献了绝大多数能量;二阶及更高阶模态占比很少。图9 仅给出了前2 阶模态,可见一阶模态反映了河段河床边界的时均形态,二阶模态反映南京段河床边界在猫子山对岸和长江村附近出现了较大变化。

图8 南京河段河床边界序列各阶模态含能Fig. 8 Energy content of POD modes of the river boundary sequence of the Nanjing reach
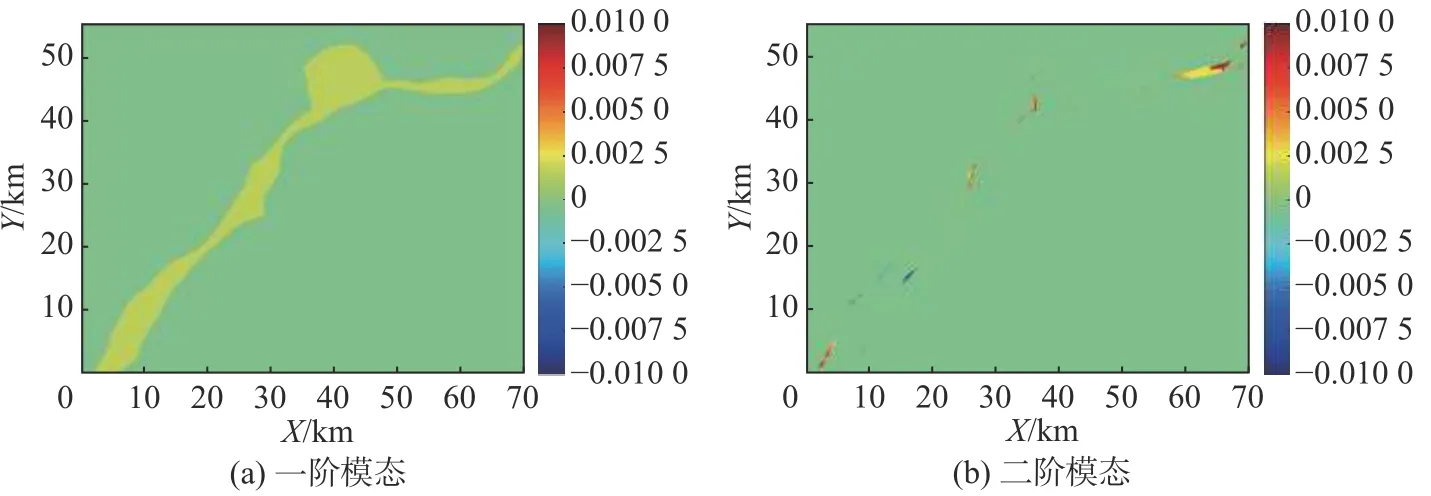
图9 南京河段河床边界序列的主要含能模态(0 为非河床,1 为河床)Fig. 9 The most energetic POD modes (1st-2nd) in river boundary sequence of the Nanjing reach
图10 为南京段河床边界序列的前两阶模态投影系数随时间的变化。可知一阶模态的投影系数随时间基本不变,数值约为600,表明一阶模态反映恒定不变的空间特征,对应河床边界的时均形态。二阶模态的投影系数随时间递减,表明在1984—2005 年间长江村附近的河床边界不断向内收缩,并在2005 年后基本保持不变。投影系数反映了长江村附近河床边界变化的时间演变特征。
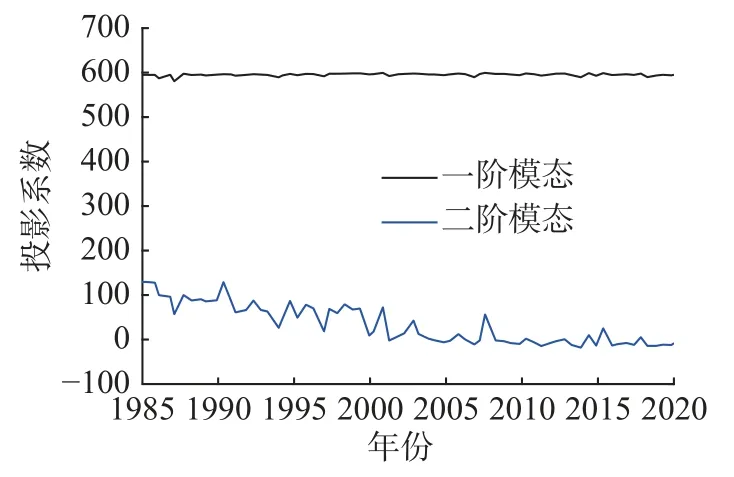
图10 一阶及二阶模态投影系数随时间的变化Fig. 10 Variation of projection coefficients of 1st and 2nd modes with time
2.3 洲滩平面演变特征
图11 为南京河段近40 年的洲滩面积随时间变化情况,八卦洲、梅子洲、新潜洲、新济洲及新生洲的面积提取相对误差分别为1.5%、4.4%、6.8%、4.7%和4.3%。八卦洲、梅子洲及新济洲较为稳定、变化较小;新生洲变化较大,表现为洲头消退和洲尾淤长,但两者程度相近,导致面积变化很小;新潜洲洲尾淤长严重,面积增幅200%,但此处几乎无人类活动,洲尾淤长主要由水沙变化所致。

图11 近40 年南京河段洲滩面积随时间变化Fig. 11 Temporal variation of sandbar areas in the Nanjing reach in recent 40 years
由于洲滩数量较多,为避免文章冗余,仅以变化较大的新潜洲为例进行分析。由图12 可知,近40年内,新潜洲的洲头变化较小,洲尾出现剧烈变化,洲尾增长甚至超过了原洲岛长度的1.5 倍。

图12 近40 年新潜洲形态统计参数Fig. 12 Statistical parameters of the Xinqian Sandbar shape sequence in last 40 years
利用本征正交分解法提取新潜洲时间序列的主要含能模态,一阶模态含能比例较高为83%,二阶至四阶模态含能比例在1%~10%,更高阶模态含能比例均在1%以下。图13 仅给出前四阶模态,可见模态分析法可以很好地提取不同时段新潜洲的淤长特征,其中一阶模态反映了洲滩的初始形态,三阶、二阶及四阶模态分别反映了洲尾的初期、中期及后期增长规律。

图13 新潜洲形态序列的主要含能模态(0 为非洲滩,1 为洲滩)Fig. 13 The most energetic POD modes (1st-4th) in shape sequence of the Xinqian Sanbar
图14 为新潜洲形态序列的前四阶模态的投影系数随时间的变化情况。可知一阶模态的投影系数随时间变化较小,表明一阶模态反映1 个较为恒定的空间特征,对应时均形态。三阶模态的投影系数在1984—2000 年呈递增趋势,此后基本不变,反映出洲尾初期增长的时间演变特征。二阶模态的投影系数在2000—2005 年呈递增趋势,此后改变很小,反映出洲尾中期的增长时间特征。四阶模态的投影系数在2005—2020 年呈递增趋势,反映出洲尾后期增长的时间演变特征。综合可知,新潜洲在近40 年内始终处于洲头稳定、洲尾淤长的状态。
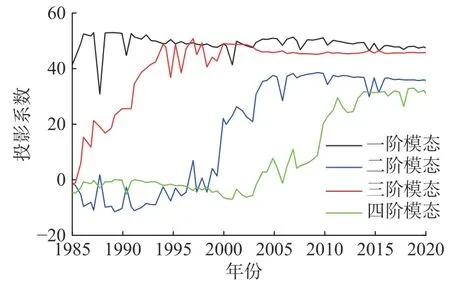
图14 一阶至四阶模态投影系数随时间的变化Fig. 14 Variation of projection coefficients of 1st-4th modes with time
3 结 语
本文利用收集的1984—2020 年间Landsat 卫星的南京段卫星遥感图片,通过目视解译及水位(拍摄日期)筛选,挑选出74 幅图片(每年2 张)。以85 高程5 m 水位为水边线提取基准,采用归一化差分水体指数来凸显河段水边线信息,采用形态学方法提取河床边界和内河洲滩,并利用本征正交分解法分析两者的空间与时间演变特征,其中含能模态反映了河道的空间演变特征,投影系数反映了时间演变特征,主要结论如下:
(1)近40 年来,长江南京段水域面积从最大的340 km2下降至320 km2,减幅6%,河床边界改变最大的区域位于长江村附近,此处边界向内收缩范围占近40 年总变化面积的52%,主要由水产养殖和围河造田导致。本征正交分解一阶模态反映了河床边界的时均形态,二阶模态反映了猫子山对岸和长江村附近河床边界的收缩变化,投影系数表明该变化主要出现在1984—2005 年间。
(2)长江南京段的八卦洲、梅子洲及新济洲的洲滩面积变化较小,均值分别为67、18、10 km2;新生洲洲头消退和洲尾淤长的面积相近,导致面积变化较小,为11 km2;而新潜洲自洲头向下游逐年淤长,增加的长度甚至超过了原洲岛长度的1.5 倍,面积为6 km2,总增幅200%。一阶模态反映了洲滩的初始形态,三阶、二阶及四阶模态分别反映了洲尾的初期、中期及后期增长规律。模态投影系数可知洲尾初期、中期及后期增长分别发生在1984—2000 年、2000—2005 年及2005—2020 年。
(3)本文应用的本征正交分解方法可以从看似无序的河床演变时间序列中提取其主要空间演变特征,并刻画这些主要空间演变特征随时间的演化规律。鉴于目前中等分辨率卫星图像的易获取性,对于其他河流,特别是偏远地区缺少实测资料的河流,应用本文方法可以很好地研究其时空演变特征。

