缠绕型碳纳米管增强陶瓷基复合材料的有效刚度和应力分析
宋瑞兰,罗冬梅,汪文学
(1.河北世洋工程检测有限公司, 河北 衡水 053000; 2.佛山科学技术学院土木工程系, 广东 佛山 528000; 3.日本九州大学应用力学研究所,福冈县 816-8580)
0 引言
1991 年,日本电子公司(NEC)的饭岛博士发现了一种质量轻,六边形结构连接完美的一维纳米材料-碳纳米管[1]。与传统的碳纤维增强材料相比,该材料具有独特的力学、热学和电学性能[2-4],其力学、热学和电学性能比传统碳纤维都有大幅度的提高[2-4],是复合材料理想的增强体,相对于普通纤维增强复合材料而言,具有无可比拟的优越性[5]。然而,碳纳米管的弯曲、缠绕等几何特性在某种程度上限制了其独特性能在最大限度上的发挥。近30年来,关于碳纳米管特性对增强复合材料力学性能的影响的研究方兴未艾[6-8]。王宏颖等[9]总结了近年来碳纳米管增强复合材料的微观结构、变形和强化机理的数值模拟的研究现状。Chander Kant Susheel[10]用数值模拟方法研究了功能梯度碳纳米管增强壳体材料的力学性能,证明了数值模拟方法研究碳纳米管复合材料的可行性。周应龙等[11]采用分子动力学方法简化的碳纳米管等效纤维模型,利用具有精确周期性边界条件的宏微观均质化理论分析正弦余弦波型非连续碳纳米管的有效刚度和局部应力分布规律。结果表明,碳纳米管稍有弯曲就会导致复合材料有效刚度降低和应力传递能力的下降。马一凡等[12]采用细观代表性体积单元模型分析基体开裂和界面脱粘2种模式引起的横向破坏,验证了计算模型的准确性。Shweta Paunikar等[13]利用连续介质力学理论,结合多相复合材料微观力学模型和能量法则,计算了碳纳米管增强复合材料在不同弯曲情况下的有效弹性常数,证明碳纳米管的曲度会导致碳纳米管增强复合材料纵向弹性模量的降低、横向弹性模量的增加,且碳纳米管越短、影响越显著。目前,碳纳米管几何形状的研究主要侧重于直线型和弯曲型[14],有关缠绕型碳纳米管增强复合材料至今未曾有人进行研究,对碳纳米管缠绕的研究将有利于进一步研究碳纳米管的团聚现象。因此,本文在文献[15]的基础上,利用均质化法计算缠绕型和余弦波型碳纳米管增强复合材料的力学性能,通过模拟缠绕型和余弦波型碳纳米管直径、长度、曲度和各向异性等的变化情况,分析缠绕型碳纳米管增强复合材料的有效刚度和应力。
1 精确周期性边界条件的均质化法
参考文献[14],假设图1所示为具有周期性微结构的线弹性体,Ω为线弹性体的三维宏观部分,Γ为Ω的边界,Y为周期性胞元,SY为Y的边界。图2为含任意周期性碳纳米管的长方体胞元。
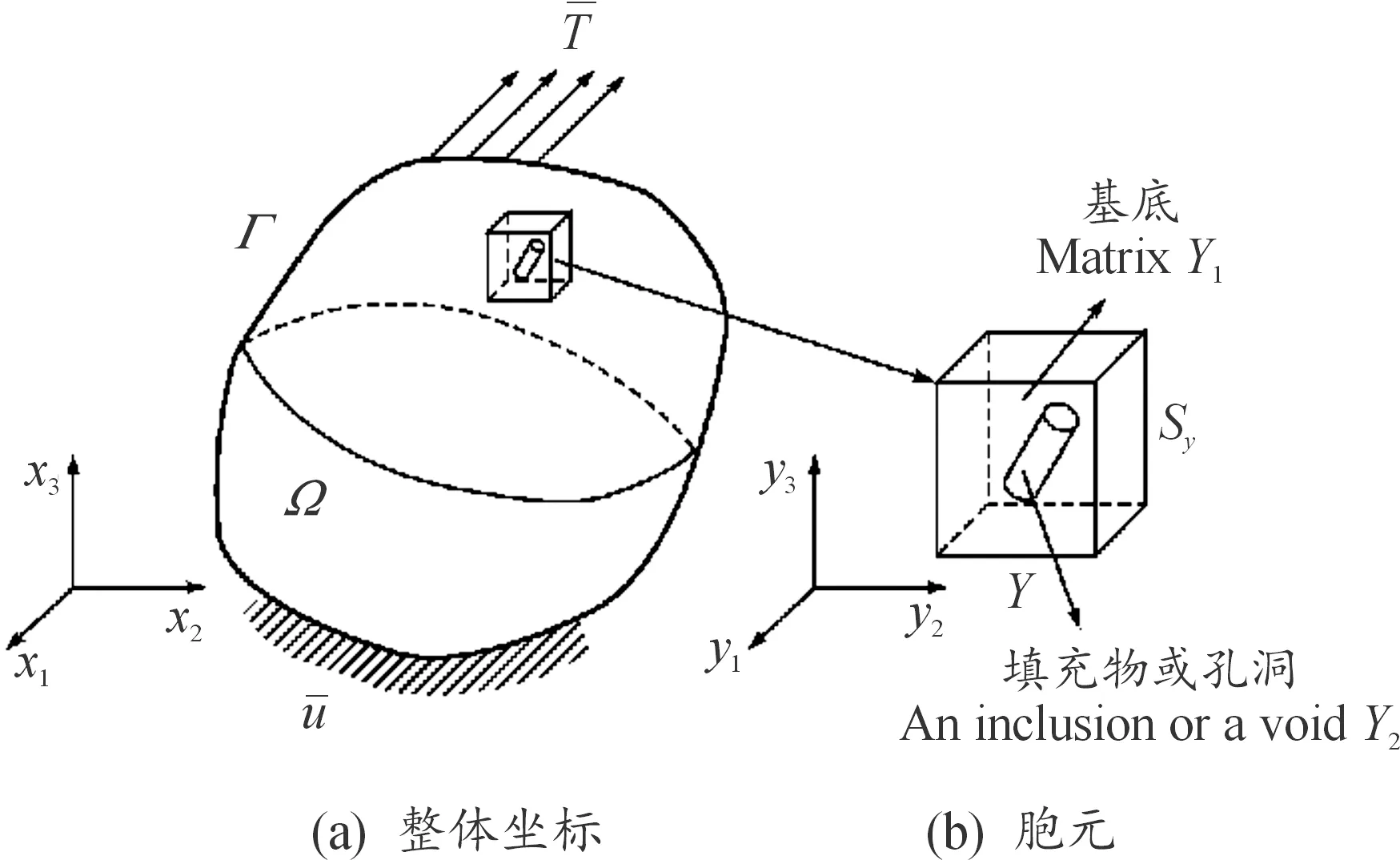
图1 宏微观坐标Fig.1 Macro-microscopic coordinate

图2 含任意周期性碳纳米管的长方体胞元
参考文献[14]所述的多尺度均质化法,考虑摄动参数η,宏观体的位移可表示为

(1)
式中:x=(x1,x2,x3)代表宏观坐标系,y=(y1,y2,y3)代表微观坐标系,其关系可由摄动参数表示为

(2)
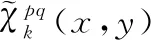

(3)
进而得到均质化弹性常数
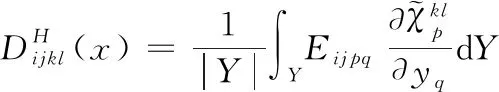
(4)
在ANSYS平台求得方程(3)的解,将其代入方程(4)求出碳纳米管增强复合材料的有效刚度,再代入应力计算公式即可分析缠绕型碳纳米管和基体的局部应力。
2 三维计算模型的构建
假设空心碳纳米管在陶瓷基体中完全分散,取向一致且呈规则排列,界面结合完美,无界面滑移和脱粘等损伤,仅考虑复合材料的弹性性能,忽略塑性性能及残余热应力的影响。采用ANSYS中的SOLID185单元建立缠绕型和余弦波型空心碳纳米管模型,典型特征体积单元的有限元网格分别如图3(a)、图3(b)和图3(c)所示,取整体模型进行数值模拟。设模型长度为150 nm,横截面取边长为30 nm的正方形,空心碳纳米管的直径为d,波长为λ。材料参数:碳纳米管的弹性模量Ef=700 GPa,泊松比vf=0.23;陶瓷基体的弹性模量Em=402 GPa,泊松比vm=0.23。对直线型碳纳米管,单元选择为规则的六面体单元,对余弦波和缠绕型碳纳米管,不规则四面体单元更能匹配弯曲型碳纳米管和基体,但在碳纳米管的交叉处和端部需要进行网格细化避免应力集中导致结果不收敛,提高计算结果的精度。

图3 特征体积单元有限元网格
3 结果和讨论
3.1 碳纳米管直径对缠绕型碳纳米管增强复合材料弹性模量的影响
首先设碳纳米管长度为常数(120 nm),分析不同直径的碳纳米管对碳纳米管增强复合材料力学性能的影响。碳纳米管壁厚为1 nm,直(外)径分别取:4、6、8、10、12 nm,其他材料参数不变。
为比较结果的合理性,图4列出了用混合法则、参考文献[16]和Halpin-Tsai[17]计算的直线型碳纳米管复合材料弹性模量的结果。
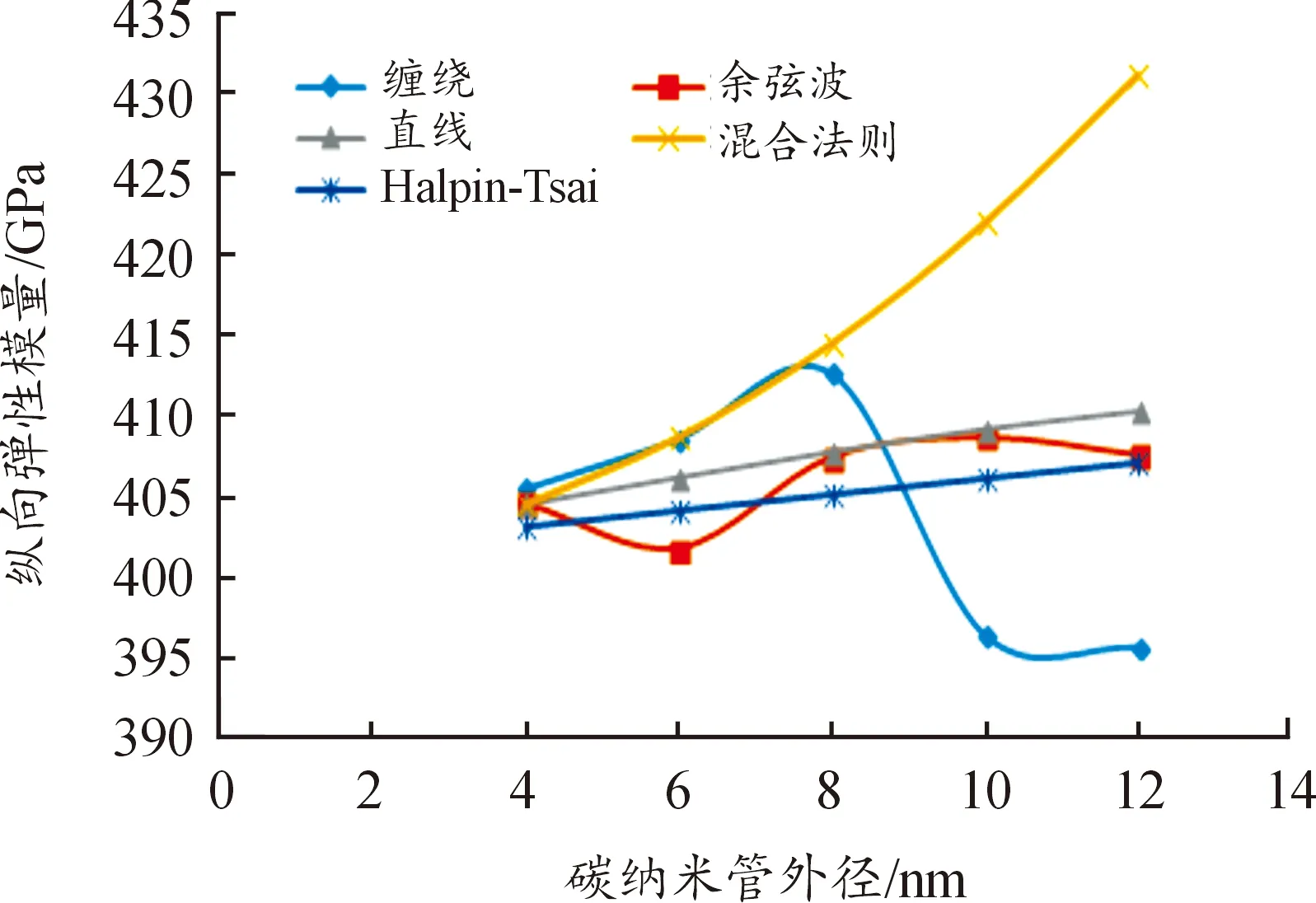
图4 纵向弹性模量与碳纳米管外径的关系Fig.4 Longitudinal elastic modulus &outer diameter of CNTS
图4、图5为直线型、余弦波型和缠绕型3种几何形状的碳纳米管的直径变化情况下,碳纳米管增强复合材料纵横向弹性模量的变化规律。

图5 横向弹性模量与碳纳米管外径的关系
由图4可知,对直线型碳纳米管复合材料,混合法则过高估计有效弹性模量,Halpin-Tsai准则预测的纵向有效弹性模量与用本文数值模拟方法得到的结果非常接近,证明数值模拟方法的可靠性。余弦波型碳纳米管和缠绕型碳纳米管复合材料的纵向弹性模量均由直线变成曲线,直径小于8 nm时,缠绕型复合材料的纵向弹性模量高于其他几种形状,碳纳米管直径超过8 nm后,缠绕型复合材料的纵向弹性模量急剧下降,远低于其他几种形状。图5横向有效弹性模量的结果与纵向弹性模量类似,碳纳米管的缠绕导致有效弹性模量发生突变。有效剪切模量在碳纳米管直径小于8 nm之前相差不大,碳纳米管直径超过8 nm后也急剧下降,直径较小时,双根碳纳米管具有增大纵向弹性模量的效应,直径超过一定尺寸后,碳纳米管之间的耦合效应导致有效力学性能发生突变,因此,当碳纳米管缠绕在一起时,碳纳米管的直径最好能保持在8 nm范围内,以避免复合材料弹性模量的骤减。图6为有效剪切模量与碳纳米管外径的关系,图7为有效泊松比与碳纳米管外径的关系。

图6 有效剪切模量与碳纳米管外径的关系Fig.6 Effective Shear Modulus &outer diameter of CNTS

图7 有效泊松比与碳纳米管外径的关系
3.2 碳纳米管长度对复合材料弹性模量的影响
设碳纳米管外径6 nm,碳纳米管沿轴线的投影长度分别为30、60、90、120、150 nm,其他材料参数保持不变。研究碳纳米管的长度对复合材料弹性模量的影响。
图8为不同计算方法得到的纵向弹性模量与碳纳米管长度之间的关系,对于直线型碳纳米管,用不同的方法得到的结果完全一致,证明了本文所用方法的准确性,余弦波型碳纳米管和缠绕型碳纳米管的纵向弹性模量随碳纳米管的形状及分布特征发生曲线变化,缠绕型碳纳米管的弹性模量弯曲程度更明显,主要原因在于直线型、余弦波型碳纳米管复合材料均为单根碳纳米管,弹性模量变化相对简单,虽然余弦波型碳纳米管的弯曲会导致碳纳米管复合材料的弹性模量呈一定的曲线变化,但变化不明显,而缠绕型碳纳米管中的2根碳纳米管之间的变形相互影响较为显著,从而导致弹性模量呈现明显的高低不同的变化。
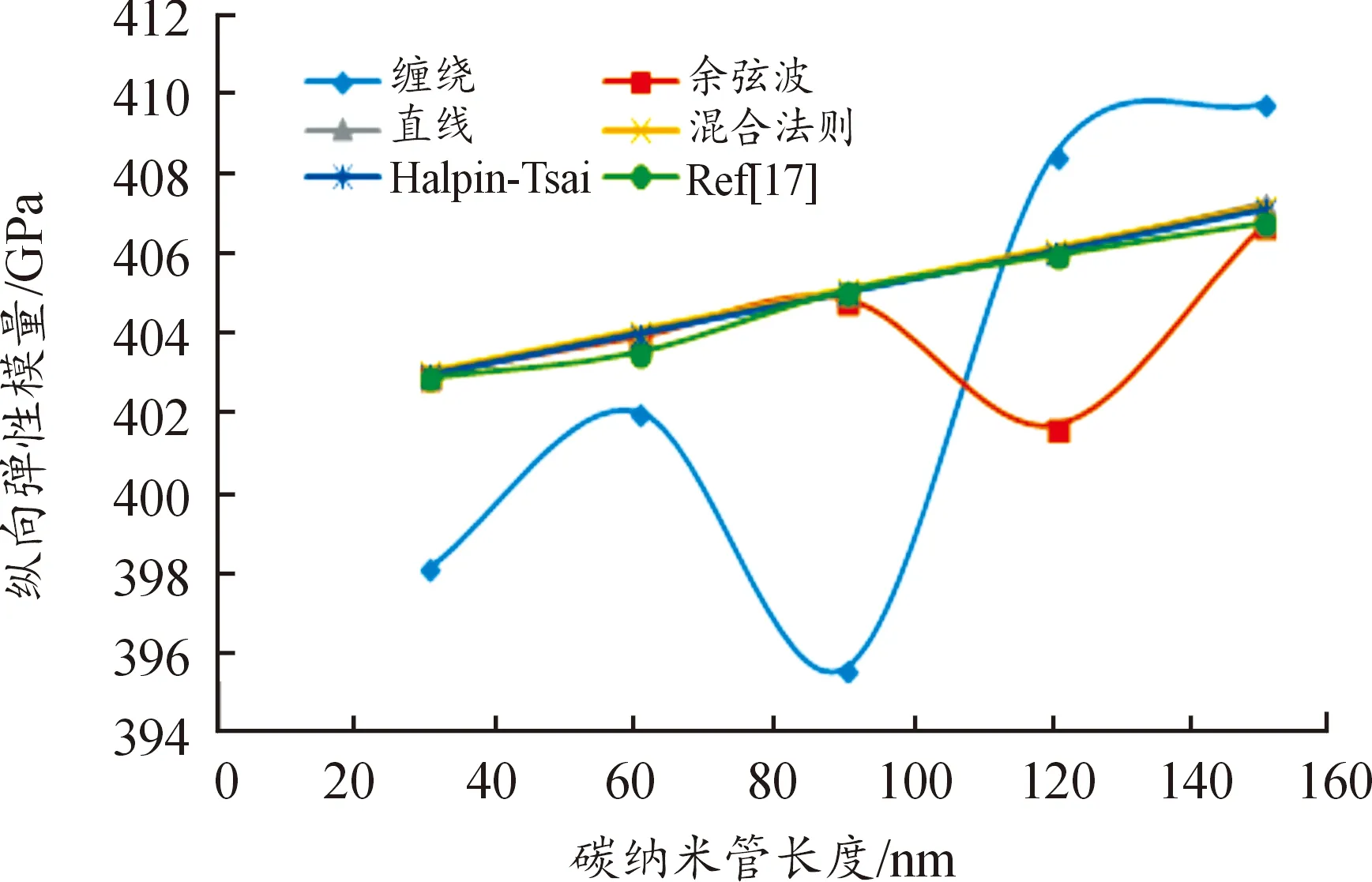
图8 纵向弹性模量与碳纳米管长度的关系Fig.8 Longitudinal elastic modulus &outer diameter of CNTS
从图9—图11发现,对直线型碳纳米管复合材料,混合法则预测的有效力学性能略高于数值模拟的结果,但变化趋势一致,余弦波型材料稍有起伏,数值与直线型结果相差不大,而缠绕型碳纳米管的弹性模量不仅远小于其他2种情况,在长度为90 nm处还会出现一个急剧变化的转折点,过此转折点之后继续呈曲线变化。由此可见,相对于直线型和余弦波型单根碳纳米管,缠绕型碳纳米管增强复合材料的尺寸效应和叠加效应较为明显,多根碳纳米管的缠绕会导致力学性能下降。
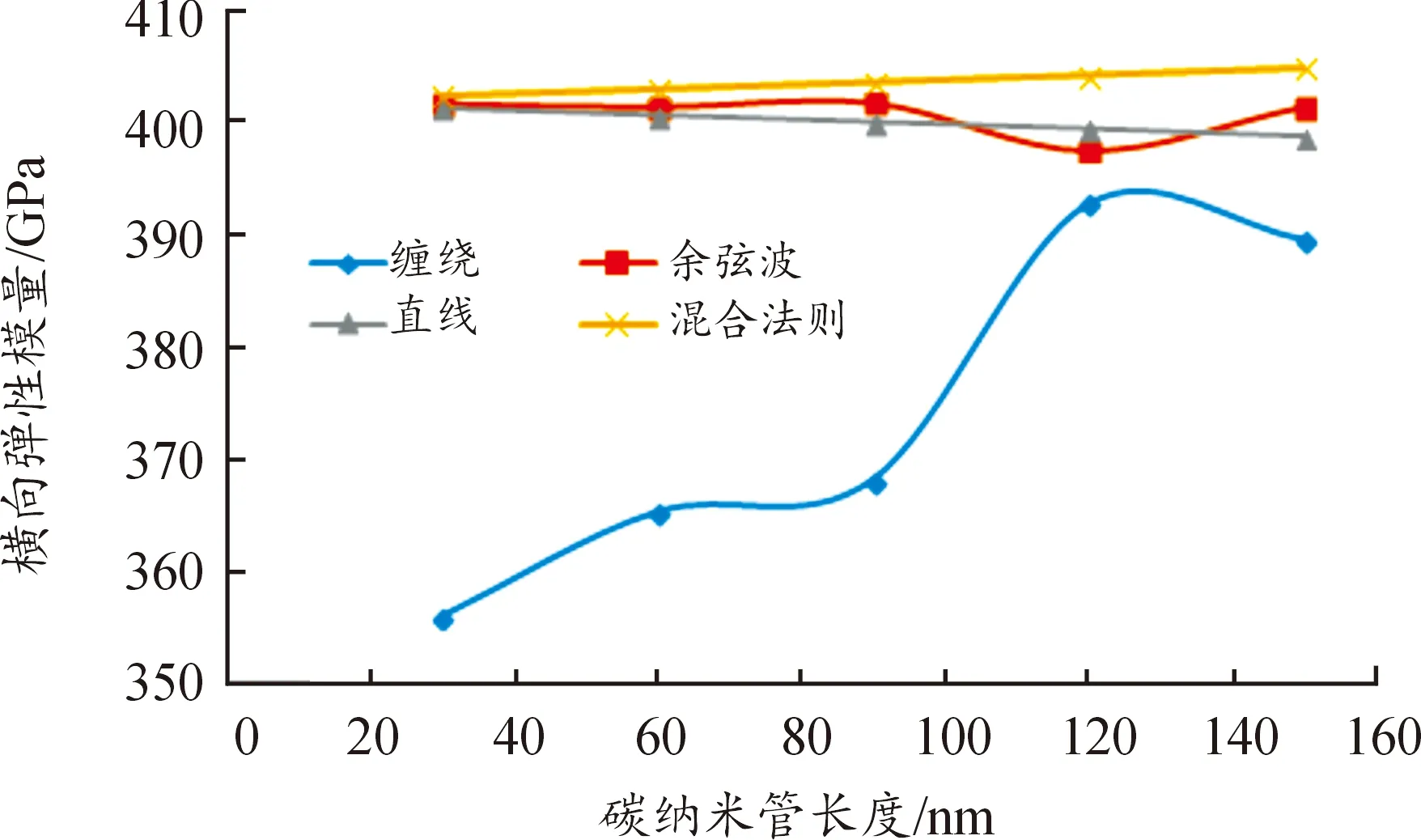
图9 横向弹性模量与碳纳米管长度的关系

图10 有效剪切模量与碳纳米管长度的关系Fig.10 Effective Shear Modulus &outer diameter of CNTS
3.3 碳纳米管各向异性对复合材料弹性模量的影响
本节主要分析碳纳米管的各向同性和各向异性对缠绕型和余弦波型碳纳米管增强复合材料弹性模量的影响。各向异性碳纳米管的弹性常数为[13]:C11=457.6 GPa,C12=C13=8.4 GPa,C22=C33=14.3 GPa,C23=5.5 GPa,C44=C66=27.0 GPa,C55=4.4 GPa,基体视为各向同性材料,缠绕型和余弦波型空心碳纳米管沿轴线方向的投影长度为120 nm,碳纳米管的壁厚为1 nm,外径分别取4、6、8、10、12 nm,其他材料参数不变。
由图12—图14可以看出,与各向同性情况不同,碳纳米管直径小于8 nm时,缠绕型复合材料的纵向弹性模量大于余弦波型,8 nm之后余弦型弹性模量继续增长,而缠绕型复合材料的弹性模量则急剧下降。余弦波型碳纳米管复合材料的模量对各向同性性质较敏感,有较大的波动,缠绕型碳纳米管材料复合材料的模量呈先大后小的波动性,且对碳纳米管的各向异性不敏感,变化趋势一致。

图12 纵向弹性模量与碳纳米管外径的关系Fig.12 Longitudinal elastic modulus &outer diameter of CNTS
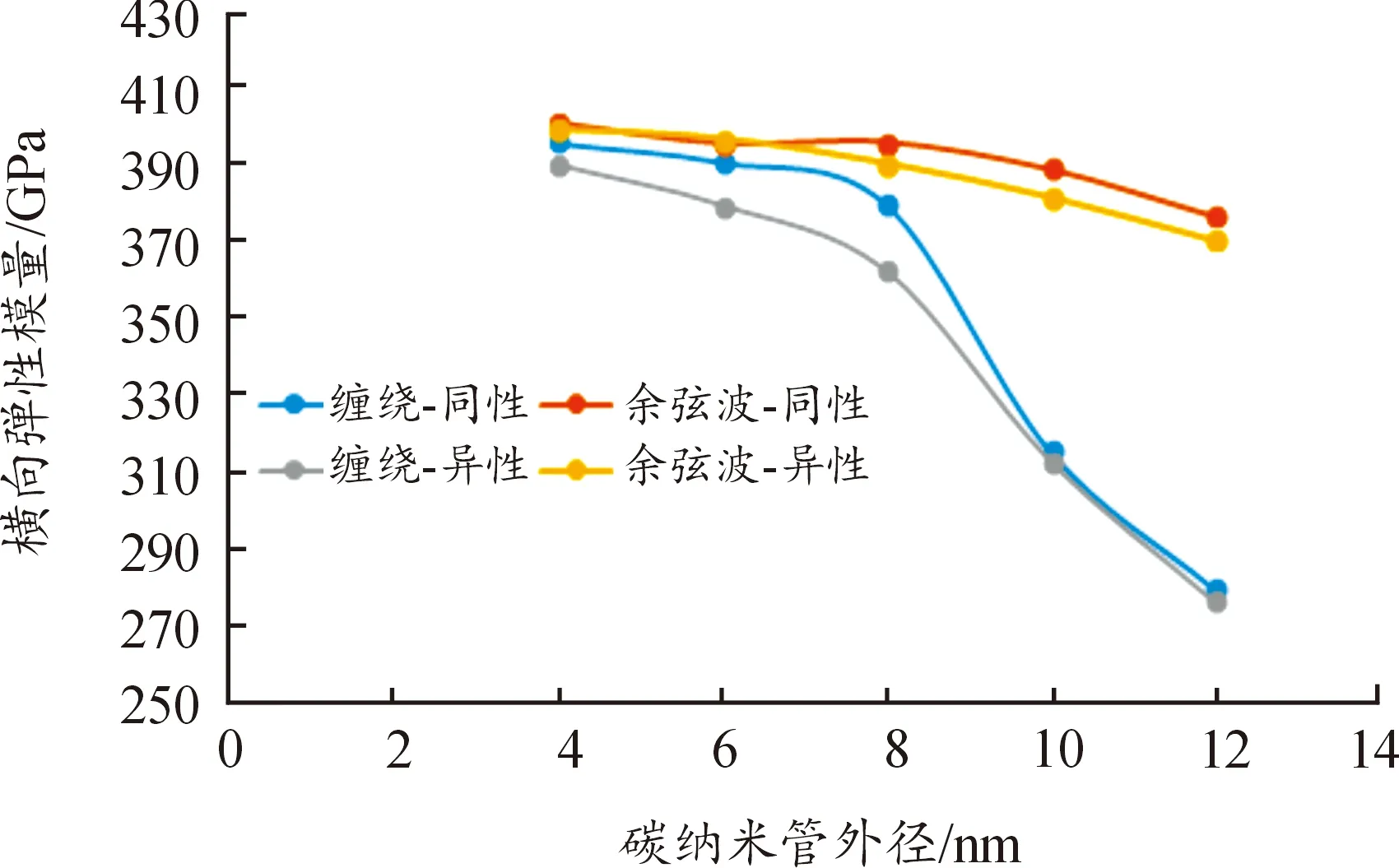
图13 横向弹性模量与碳纳米管外径的关系

图14 有效剪切模量与碳纳米管外径的关系Fig.14 Effective Shear Modulus &outer diameter of CNTS
图15显示,虽然各向异性情况余弦波型碳纳米管复合材料的泊松比比各向同性情况大很多,但变化规律基本保持一致,均随碳纳米管直径的增大而平稳上升,可见,碳纳米管的各向异性增大了余弦波型碳纳米管增强复合材料的泊松比,由此导致横向变形增大。对于缠绕型碳纳米管复合材料,当碳纳米管外径小于8 nm时,各向同性情况下的泊松比小于各向异性情况,而当碳纳米管外径超过8 nm时,两者几乎以相同的速度同时下降,碳纳米管直径超过8 nm之后,缠绕型碳纳米管的泊松比远小于余弦波型,且对材料的各向同性和各向异性不敏感,数值变化不大,由此证明由于碳纳米管之间的相互作用,削弱了材料的力学性能对缠绕型碳纳米管复合材料泊松比的影响。

图15 有效泊松比与碳纳米管外径的关系
3.4 直径对缠绕型碳纳米管增强复合材料局部应力分布的影响
图16是缠绕型各向同性碳纳米管外径为6 nm情况下,基体与碳纳米管的轴向应力分布规律。 可以看出,碳纳米管的应力梯度非常大,而且在碳纳米管两端以及缠绕交叉部位出现明显的应力集中现象,最大轴向应力可达901 GPa,而在端部管身外侧的应力最小,为320 GPa。缠绕型碳纳米管管身内侧的应力值比其外侧的应力值大得多。在碳纳米管端部及缠绕交叉附近基体的应力出现应力集中的现象,而其他部位的应力变化基本平稳。这表明,对缠绕型碳纳米管复合材料而言,碳纳米管端部和缠绕交叉这2个区域是破坏的危险点,在基体无缺陷的情况下发生断裂的几率最大。
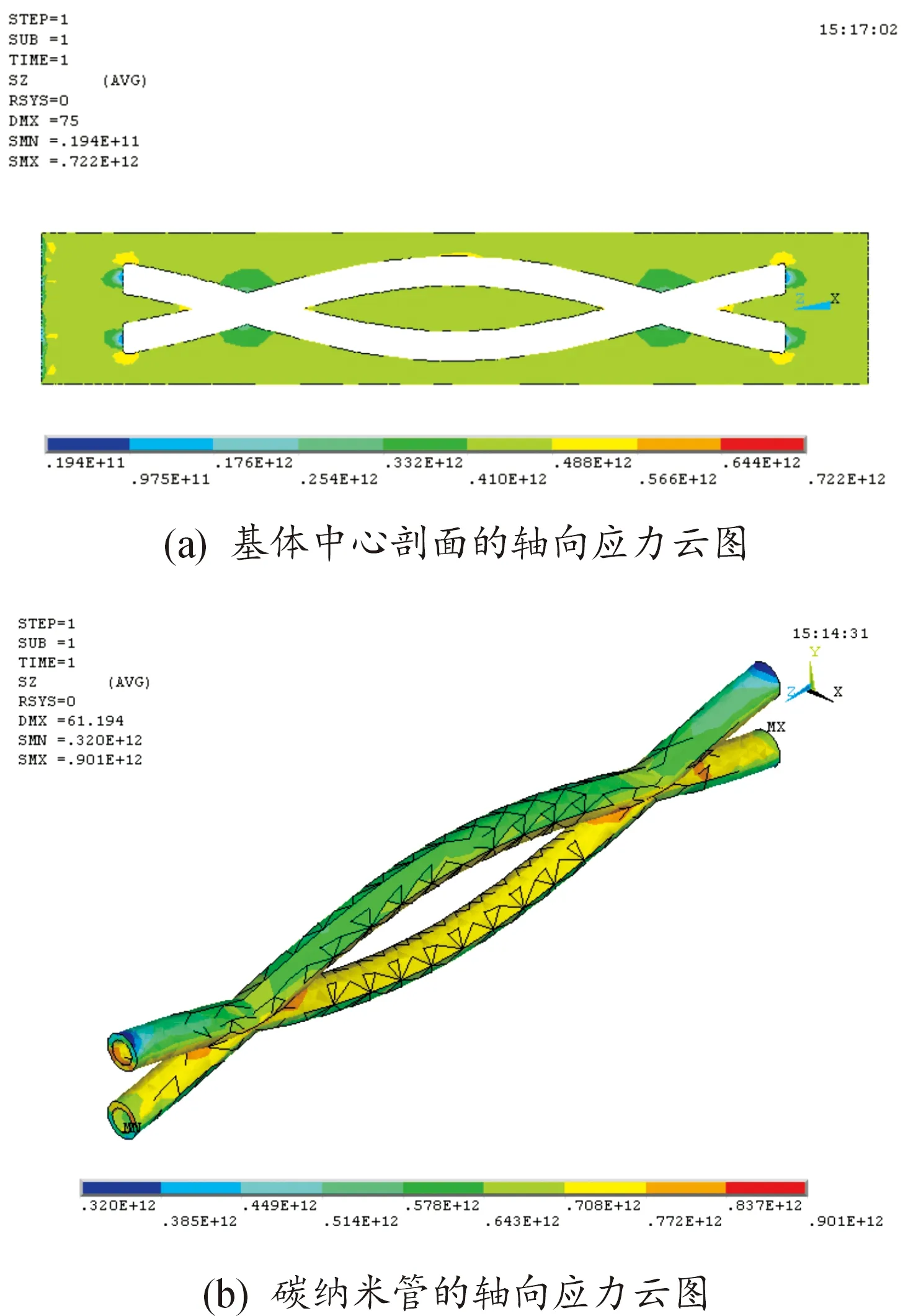
图16 碳纳米管外径d=6 nm时基体及碳纳米管的轴向应力分布示意图
表1和表2显示碳纳米管外径变化时基体和碳纳米管的最大及最小轴向应力。从其中可以看出,随着碳纳米管外径的增大,基体和碳纳米管的最大轴向应力也随之增大,相反,碳纳米管的最小轴向应力则随碳纳米管外径增大而减小,当外径超过8 nm时,碳纳米管的最小轴向应力由拉应力变为压应力,基体的最小轴向应力随外径的增大而逐渐减小。当碳纳米管外径小于8 nm时,基体的最小轴向应力随外径的增大呈增大的趋势,在8 nm处达到最大。从图16(b)看出,最大应力出现在碳纳米管缠绕交叉部位,最小应力出现在碳纳米管端部,碳纳米管外径的增大会加剧2个危险区域的应力集中。从整体来看,复合材料的轴向应力主要由碳纳米管承担,碳纳米管直径超过8 nm后,基体承受的最大应力明显增大,这与有效弹性模量的变化趋势一致,碳纳米管的有效模量骤减,导致碳纳米管的应力传递能力减小。

表1 各向同性情况下不同直径的碳纳米管的轴向最大应力和最小应力(GPa)

表2 各向同性情况下不同直径情况下基体的轴向最大应力和最小应力(GPa)
图17是外径为6 nm的缠绕型各向同性碳纳米管复合材料的基体和碳纳米管的von mises stress应力分布示意图。可以看出,碳纳米管的等效应力沿管轴线呈梯度变化,最大值出现在缠绕交叉部位,最小值则出现在碳纳米管端部;基体的等效应力分布相对均匀,碳纳米管端部和缠绕交叉部位的基体区域应力集中现象较为显著,且主要为压应力。可见,碳纳米管的缠绕特性能有效限制基体变形,发挥其对基体的增强作用。

图17 碳纳米管为各向同性材料时基体及碳纳米管的von mises stress应力分布示意图
综合图16和图17可知,碳纳米管的轴向应力和等效应力的最大和最小值都出现在缠绕交叉部位和端部,该区域的基体和碳纳米管都表现出应力集中现象,是破坏的危险点,发生断裂的几率最大。
表3和表4是碳纳米管为各向同性材料时基体和碳纳米管的最大及最小等效应力。可以看出,基体和碳纳米管的最大等效应力随碳纳米管外径的增加呈增大的趋势,且碳纳米管的最大等效应力大于基体的。碳纳米管的最小等效应力整体上随纳米碳管外径的增加而减小,外径超过8 nm之后骤减,外径为8 nm处的基体最小等效应力发生突变,达到最小值,应力变化的趋势与弹性模量的变化具有一致性。

表4 各向同性情况下基体von mises stress的最大值和最小值(GPa)
3.5 各向异性对缠绕型碳纳米管增强复合材料局部应力分布的影响
图18是各向异性碳纳米管外径为6 nm时基体和碳纳米管的轴向应力云图。与各向同性情况相比(图16),图18中陶瓷基体轴向应力都比各向同性情况小,而且变化趋势相反。碳纳米管端部外侧轴向应力最小,内侧应力逐渐增大,缠绕处应力达到最大。各向同性情况下碳纳米管轴向应力的值远大于各向异性情况,且依然是最大轴向应力出现在缠绕处、最小轴向应力出现在碳纳米管端部。可见,碳纳米管的各向异性导致碳纳米管轴向应力大幅度降低,不利于发挥碳纳米管在复合材料中的增强作用。

图18 碳纳米管为各向异性材料时基体及碳纳米管的轴向应力分布示意图
表5和表6是各向异性的碳纳米管外径变化时,基体和碳纳米管的最大及最小轴向应力变化情况。由其中数据可以看出,基体和碳纳米管的最大及最小应力随碳纳米管外径的增大呈非线性变化。与表1和表2相比,各向异性情况下碳纳米管的最大及最小应力远小于各向同性情况下的值,且其最小应力均为压应力;而基体的轴向最大应力则大于各向同性情况。整体看来,碳纳米管为各向异性材料时,复合材料的轴向应力主要有基体承担,碳纳米管承担的应力非常小,由此可见,碳纳米管的各向异性大大降低了碳纳米管在复合材料中的增强作用。

表5 各向异性情况下碳纳米管的最大应力和最小应力(GPa)

表6 各向异性情况下基体的轴向最大应力和最小应力(GPa)
图19是外径为6 nm的缠绕型碳纳米管为各向异性材料时,基体和碳纳米管的von mises stress应力分布示意图。由图19(a)可以看出,碳纳米管的外围区域的等效应力为最小压力,且分布均匀,在其相对的内侧区域,碳纳米管的等效应力逐渐增加。基体的等效应力分布如图19(b)所示,碳纳米管端部的基体区域有应力集中,且基体的等效应力为最小压力,碳纳米管缠绕部位的基体等效应力比端部的等效应力略大,但依然为压应力。与图17(b)相比,碳纳米管为各向同性时,碳纳米管缠绕部位周围的基体等效应力值为252 GPa;而碳纳米管为各向异性时(图19(b)所示),碳纳米管缠绕部位周围的基体等效应力值为247 GPa,从数值上看,各向异性情况比各向同性情况的小,但从影响范围看,各向异性情况碳纳米管缠绕部位周围的基体影响区域比各向同性情况的大。因此,缠绕型碳纳米管的各向异性对基体变形具有更好的限制作用。
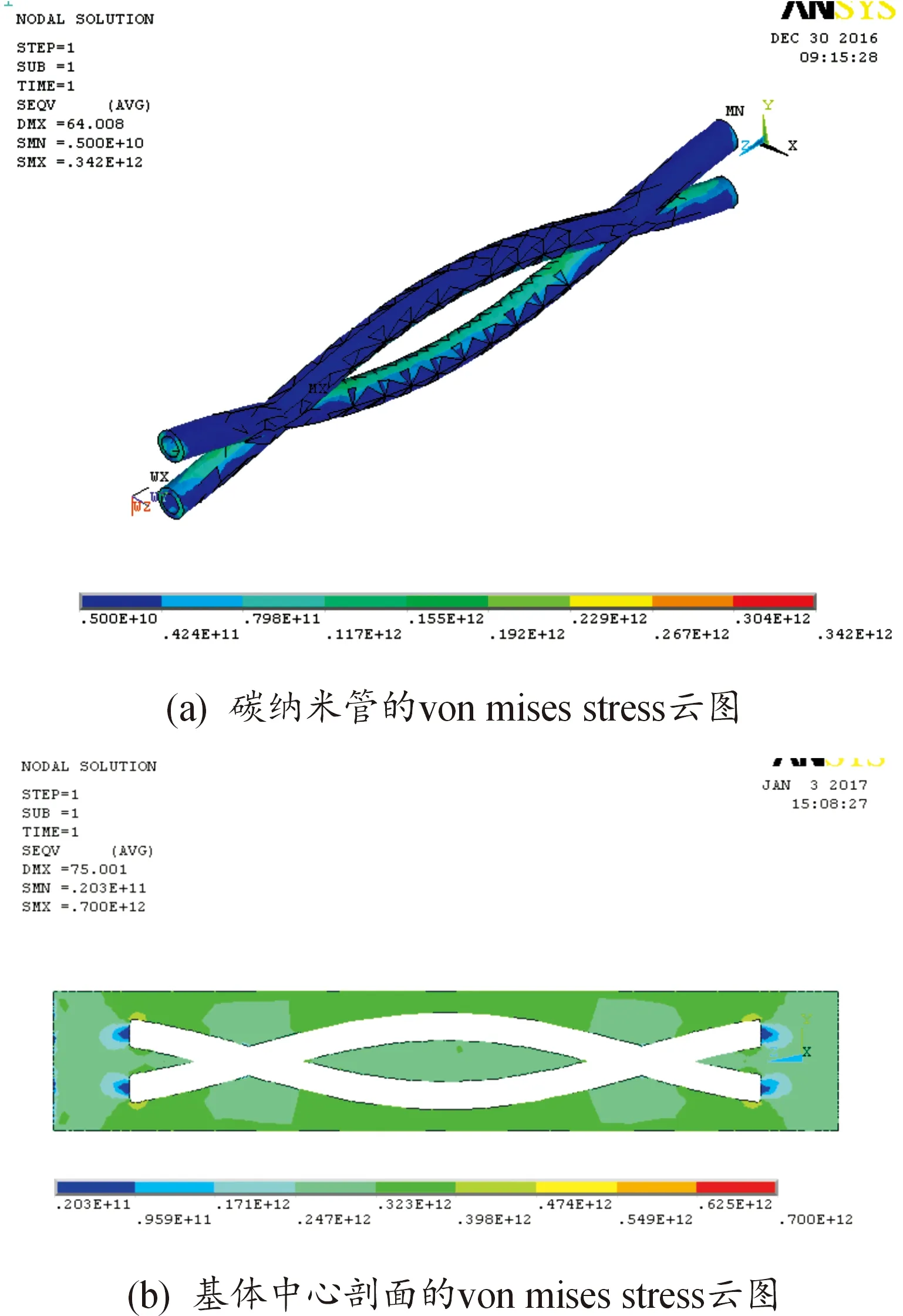
图19 碳纳米管为各向异性材料时基体及碳纳米管的von mises stress应力分布示意图
与碳纳米管为各向同性的情况相比(表3和表4),碳纳米管为各向异性时(表7和表8),无论应力最大、最小值还是Von mises应力最大、最小值,碳纳米管承受的应力均明显降低,而基体的应力明显增大,由此说明各向异性碳纳米管复合材料中的碳纳米管传递应力的能力明显减弱,忽略碳纳米管的各向异性会导致过高估计复合材料的承载能力。

表7 各向异性情况下碳纳米管von mises stress的最大值和最小值(GPa)

表8 各向异性情况下基体von mises stress的最大值和最小值(GPa)
4 结论
利用均质化法模拟直线型、余弦波型和缠绕型碳纳米管的尺寸变化对碳纳米管增强复合材料力学性能的影响。主要结论如下:
1) 与直线型碳纳米管相比,余弦波型和缠绕型碳纳米管增强复合材料的力学性能更容易受碳纳米管尺寸因素的影响,缠绕型碳纳米管的有效力学性能受碳纳米管的相互作用影响,呈典型的曲线变化,碳纳米管的外径为8 nm时,缠绕型碳纳米管复合材料的弹性模量会产生突变,碳纳米管的缠绕特性对横向变形有更好的限制作用。
2) 碳纳米管的长度变化引起余弦型和缠绕型碳纳米管复合材料的有效力学性能呈成曲线变化,碳纳米管长度为90 nm时,缠绕型碳纳米管材料的有效力学性能急剧降低、尺寸效应和叠加效应更加明显,多根碳纳米管的缠绕会导致力学性能下降。
3) 碳纳米管的各向异性增大余弦波型碳纳米管增强复合材料的泊松比,导致横向变形增大。但是,碳纳米管的各向异性在外径超过8 nm后,缠绕型碳纳米管复合材料的泊松比急剧下降,可有效约束复合材料的横向变形。
4) 碳纳米管端部和缠绕交叉部位均有明显的应力集中现象,是破坏的危险点,在基体无缺陷的情况下该区域断裂的几率最大。碳纳米管外径为8 nm时,基体和碳纳米管最大、最小应力发生转折,缠绕型碳纳米管复合材料的尺寸效应最为显著。

