基于自适应滤波的磁梯度数据三维相关成像

黄双龙，邱 景，*，孙赫轩，张顺雨，兰 天

（1.重庆大学 光电工程学院，重庆 400044；2.光电技术及系统教育部重点实验室，重庆 400044）

0 引言

当前水下成像技术主要是利用光学或声学等手段在水下获取目标或环境的图像信息。水下光学成像可以提供高分辨率、符合人眼视觉特征的图像，但受限于能见度，特别是在浑浊的水体中，光学成像的有效距离很短，难以实现大范围的海底探测。声波在水中的衰减远比电磁波小，可以实现超远距离的水下探测和通信。但声波的波长与频率成反比，高频声波具有较高的分辨率，而衰减较快，低频声波具有较远的传播距离，而分辨率较低，难以同时满足高分辨率和远距离的要求。由于水下目标（管道、线缆、沉船等）大多数带有磁性，而磁异常信号具有不易受海水、泥沙等介质影响的优点，适合用于掩埋物的探测，因此磁学成像技术被越来越多地应用于探测水下目标[1-3]。

磁学成像技术主要分为磁化率成像法和相关成像法。磁化率成像法可以根据磁场数据来推断水下磁性体的位置、形状、大小和磁化强度等大量信息，有利于识别水下目标的类型。但是在缺乏先验信息的条件下，磁化率成像算法计算速度慢，可能陷入局部最优解或收敛困难[4-6]。而相关成像技术则是计算实测磁异常与地下各点产生的磁异常的归一化互相关系数，并用相关系数的极大值位置估计磁性体的中心位置，过程简单、稳定、易于实现[7]。因此相关成像技术可以作为磁化率成像的前置步骤，提供磁性体的位置先验信息，改善磁化率成像效果。

MAURIELLO等首次将相关成像法用于磁性目标的定位，通过应用Schwarz不等式，导出了用于成像磁异常源分布的发生概率函数[8]。由于完全忽略先验信息，相关成像方法的纵向分辨率较差，除了简单和孤立的磁性体外，它无法区分分布在复杂或紧密间隔情况下的磁性体，因此对于不同深度的多磁性目标，相关成像的效果不佳[4，9]。目前已经有许多研究对相关成像进行了改善，GUO等提出了一种新的磁场总异常垂直梯度相关成像方法，证明了垂直梯度数据的三维相关成像比单独使用磁场总异常的分辨率更高[10]。马国庆等改进了相关成像技术，减小了磁性体的实际形状与通常使用的球体形状差别较大时所产生的计算误差，但难以对叠加场进行处理[11]。李金鹏等人提出了基于磁梯度张量的地下小目标相关成像方法，通过迭代计算将概率密度分布转化为实际的物性参数分布[12]。SUN等从相关成像结果中提取空间变化，然后将其转换为空间加权函数添加到模型目标函数中，获得了具有更高可靠性的结果[13]。MA等利用磁异常数据的局部波数和假设源生成的合成数据的局部波数的相关系数来计算磁源的深度[14]。马国庆等接着提出了重磁不同阶梯度比值相关成像法，该方法可以准确计算出磁性体的中心位置，且在二阶及以上导数计算时采用Laplace方程来完成，具有良好的抗噪性[15]。林涛等在均值滤波和插值切割分离的位场异常上，使用相关成像法对稳定向下延拓得到不同深度层上重力及梯度异常进行处理，提高了纵、横向成像分辨率[16]。丁亚洲推导出了不同阶次解析信号垂向导数的相关成像法，也有效提高了相关成像的分辨率[17]。总之，相关成像技术作为一种相对新型的快速自动解释方法，这些年来许多研究都在不断改善其成像效果、逐渐提高成像分辨率。

为了进一步提升对不同深度的多磁性目标的相关成像效果，本文使用快速傅里叶变换对测量平面的磁梯度数据进行处理，根据不同深度磁性体的磁梯度数据频谱特性进行自适应滤波，将滤波后的数据用于成像，有助于提升成像结果的分辨率，进一步发挥磁学成像技术在探测水下目标领域的应用。

1 磁梯度数据三维相关成像法

磁梯度张量G是磁感应强度B的3个分量各自的空间变化率。在三维直角坐标系下分别对磁感应强度B的3个分量沿X、Y、Z这3个方向求导，就能得到磁梯度张量G，其表达式为

式中：Bx、By，、Bz为磁感应强度B在X、Y、Z这3个方向上的分量；Bij（i，j=x，y，z）为磁梯度张量的各个分量。

由于地磁场通常可以看作无源静磁场，所以磁感应强度B的散度以及旋度都为0，表达式为

因此，磁梯度张量的各个分量之间并非相互独立，而是满足

根据式（3）可以得到，磁梯度张量虽然有9个分量，但其中仅有5个是独立分量，而且其构成的磁梯度张量矩阵是一个对称矩阵。

与传统的磁总场异常相比，磁梯度张量能提供更加丰富的异常信息，能更好地反映水下磁性体的细节特征[18]。此外，使用磁梯度张量的每个分量进行相关成像的效果也不尽相同，通常Bzz分量在深度方向上具有最好的成像效果[19]。由于相关成像具有横向分辨率较高、纵向分辨率差的特点[20]，本文采用Bzz分量进行相关成像。

磁梯度数据三维相关成像法的基本流程：1）将待成像的空间划分成M个均匀的三维网格；2）计算每一个网格可能存在的磁性体在观测平面引起的磁梯度数据；3）计算实测数据与计算数据的相关系数；4）将相关系数可视化，获得空间中磁性体的概率分布。

如图1所示，在笛卡尔坐标系中，取平面z=0为观测平面。假设在观测平面上某一点（xi，yi，zi）测得的磁梯度张量为Bzz（xi，yi，zi）。观测平面下的一点（ξ，η，ζ）存在一个小的长方体形的磁性体q，把它近似成一个磁偶极子，计算出它在点（xi，yi，zi）产生的磁异常为Bzz，q（xi，yi，zi）。

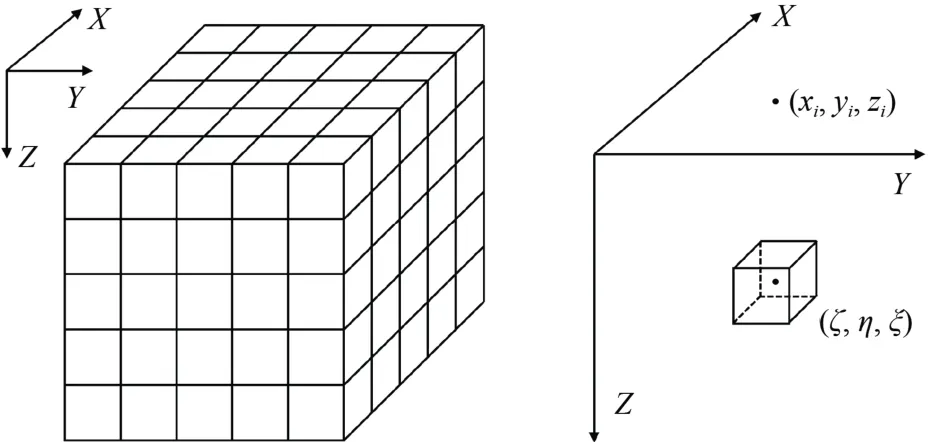
图1 相关成像原理示意图Fig.1 Schematic diagram of correlation imaging method

定义观测平面内测得的磁异常Bzz（xi，yi，zi）与磁性长方体q在观测平面上产生的磁异常Bzz，q（xi，yi，zi）的皮氏（Pearson）互相关系数为

式中，N为测量点总数。

根据柯西不等式，可知Cq的取值范围是[–1，1]。Cq表征了实测磁异常与磁性体q产生的磁异常的相关性，即实测磁异常有多大的可能性是由磁性体q产生的。Cq越接近于1，则该位置越有可能存在一个磁化率大的磁性体；Cq越接近于–1，则该位置越有可能不存在磁性体。

2 磁梯度数据的自适应滤波

在二维测量平面上得到的磁梯度数据可以等效为一张二维图像，通过快速傅里叶变换就能得到磁梯度数据的频谱。

尺寸为M×N的函数f（x，y）的DFT为

式中，u和v为频率变量。u=0，1，2，…，M–1；v=0，1，2，…，N–1。

给出F（u，v），可通过反DFT得到

式中，x和y为测量点的横坐标与纵坐标。

图2展示了不同深度的磁性体的磁梯度数据及幅度谱。在测量平面下方，浅层的小型磁性体引起的异常范围小、变化快，对应频率域的高频成分。深层较大的磁性体引起的异常范围大、变化平缓，对应频率域的低频成分。

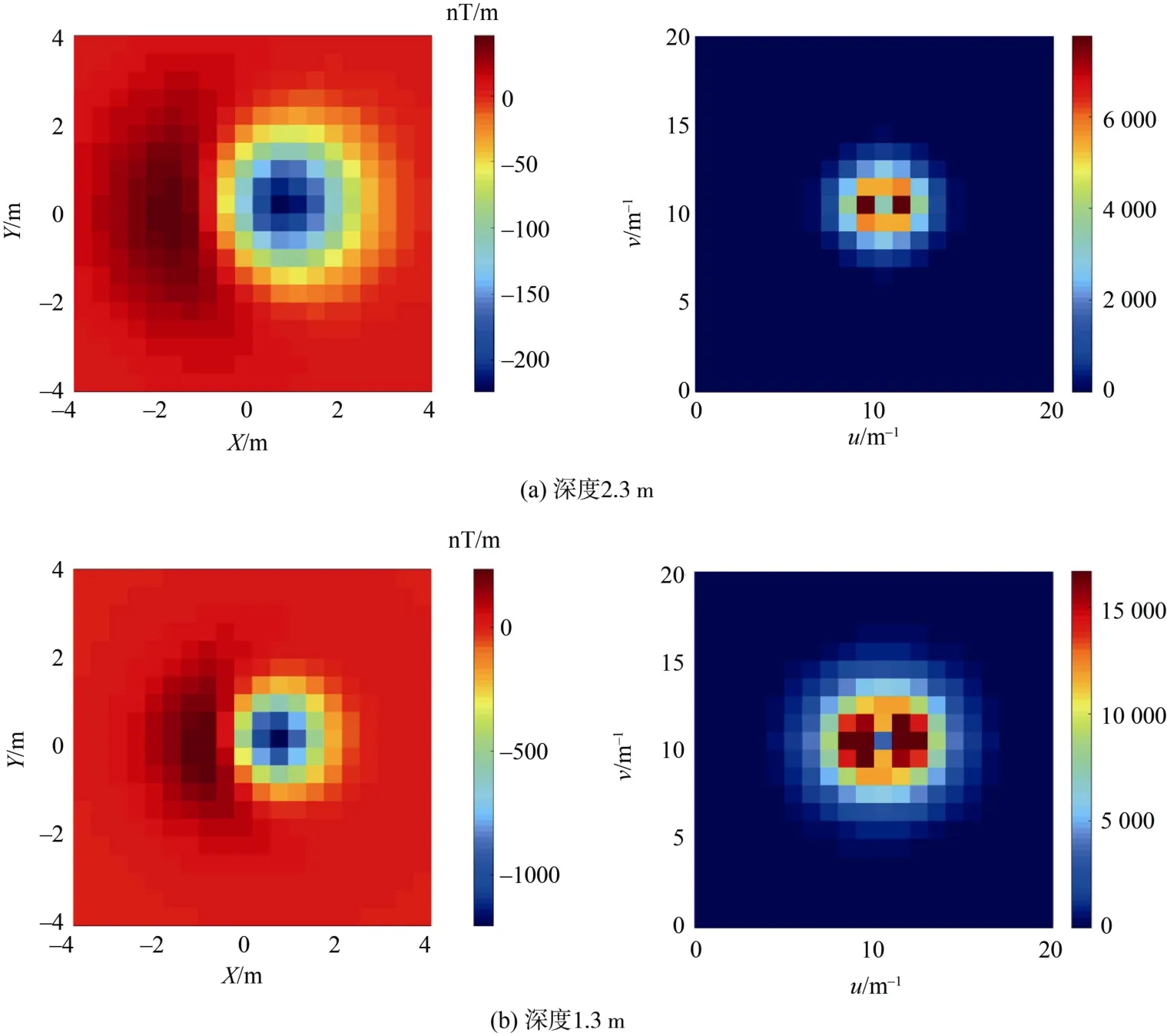
图2 不同深度的磁性体的磁梯度数据及幅度谱Fig.2 Magnetic gradient data and amplitude spectra of magnetic bodies at different depths

在磁梯度数据的相关成像过程中，如果成像空间中存在不同深度的多个磁性体，磁性体的磁场相互叠加，会导致成像结果的纵向分辨率严重降低，无法准确估计磁性体的深度。但是由于不同深度磁性体的磁梯度数据在频率域具有明显的差异，因此可以利用频率域滤波来分离不同深度的磁异常。

本文提出一种磁梯度数据的自适应滤波方法，以改善相关成像的分辨率。具体步骤是：

1）测量磁性体的磁梯度张量数据Bzz（xi，yi）；

2）将测量平面以下的空间均匀剖分成M个网格单元；

3）用解析法计算第n个网格单元的磁梯度数据Bzz，q（xi，yi），并用快速傅里叶变换得到其频谱Szz，q（ui，vi）；

4）将频谱Szz，q（ui，vi）的每一个频率分量按照幅度进行排序，保留幅度大小前50%的分量，标记其余分量并置0，然后用逆傅里叶变换得到滤波后的磁梯度数据B’zz，q（xi，yi）；

5）滤除观测数据Bzz（xi，yi）中被步骤4标记的频率分量，得到滤波后的观测数据B’zz（xi，yi）；

6）计算B’zz，q（xi，yi）与B’zz（xi，yi）的相关系数；

7）重复步骤3–6依次计算M个网格单元的相关系数，得到三维相关成像结果。

该方法的特点是依据每一个网格单元的磁梯度数据频谱来确定要保留测量数据中的哪些频率成分，而不是采用固定的频率阈值进行滤波。深处的磁性体产生的磁梯度张量低频成分居多，就滤除观测数据中的高频成分，反之则滤除观测数据中的低频成分，然后再计算两者的相关系数。

3 仿真模型实验

本文设定反演空间的水平边界范围为–2.5～2.5 m，垂直边界范围为0～2.4 m。然后把反演空间划分成立方体网格单元，每个立方体的大小都为0.05 m×0.05 m×0.05 m，共计480 000个网格单元。为确保数据能被完整观测，观测平面的范围应大于反演空间的水平边界范围。设定观测平面的范围为–4～4 m，均匀分布21×21个观测点，观测点间距为0.4 m。

为了验证所提出的三维相关成像方法的有效性，在反演空间中设置了4个长方体模型来模拟水下磁性目标。各个模型的参数设置如表1所示，模型的三维视图如图3所示。

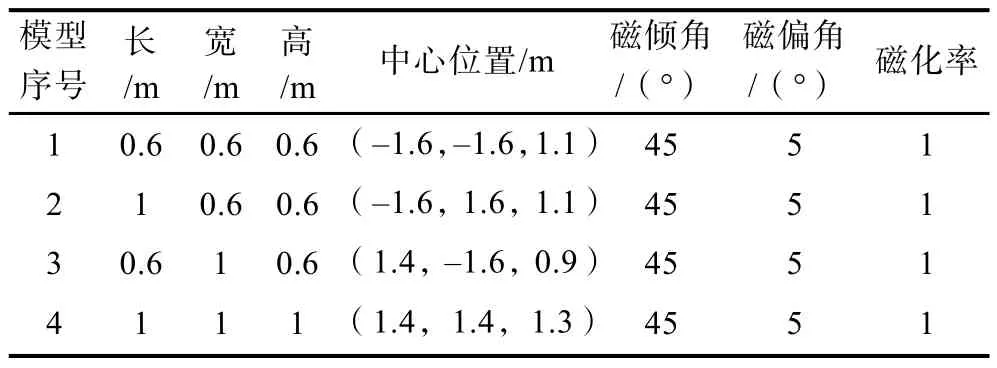
表1 模型参数设置Table 1 Model parameter settings

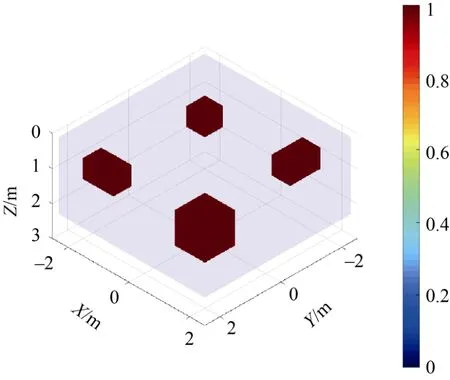
图3 模型的三维视图Fig.3 3D view of model

以解析方法在观测平面上进行正演，在高度为Z=0所计算的磁梯度张量分量理论值如图4（a）所示。考虑到实际测量环境中有噪声的影响，在理论数据中加入2%的高斯白噪声模拟含有磁测噪声的信号，含噪声信号如图4（b）。

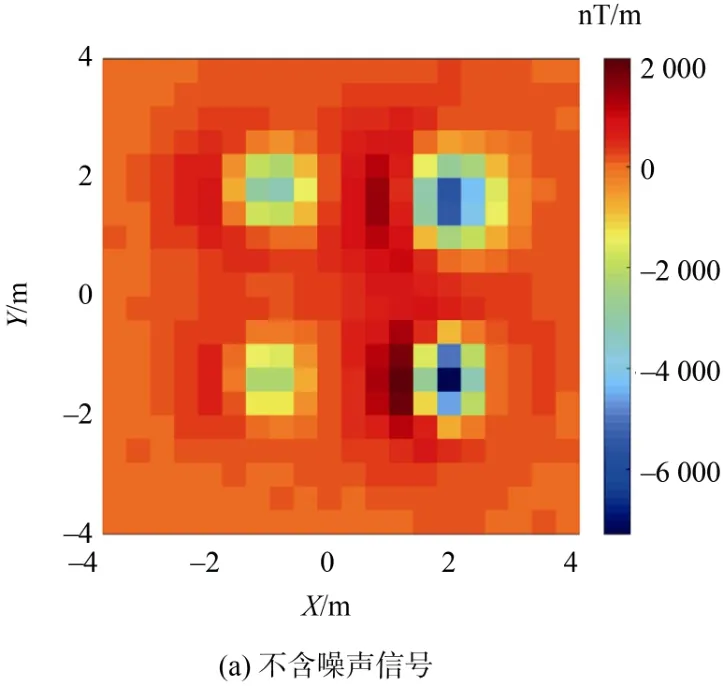
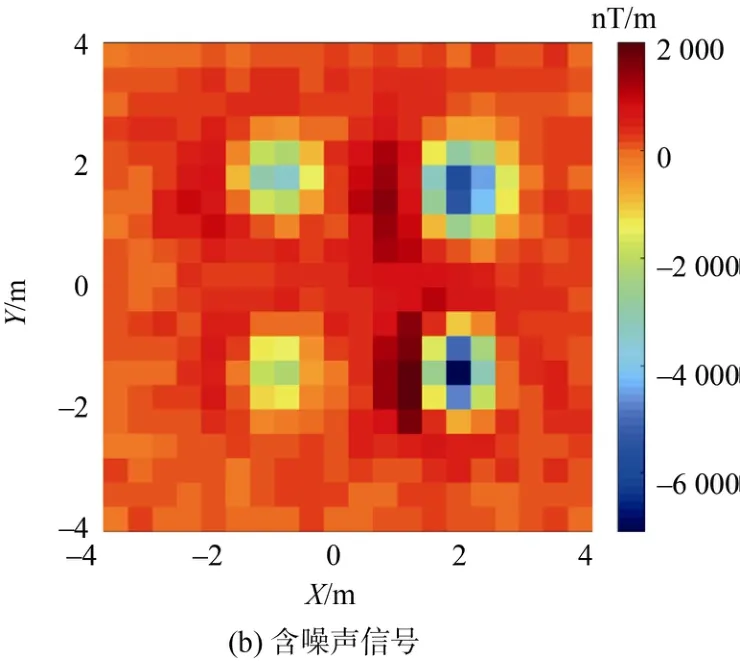
图4 模型的磁梯度数据Fig.4 Magnetic gradient data of model

用快速傅里叶变换计算磁梯度数据的频谱，结果如图5所示。

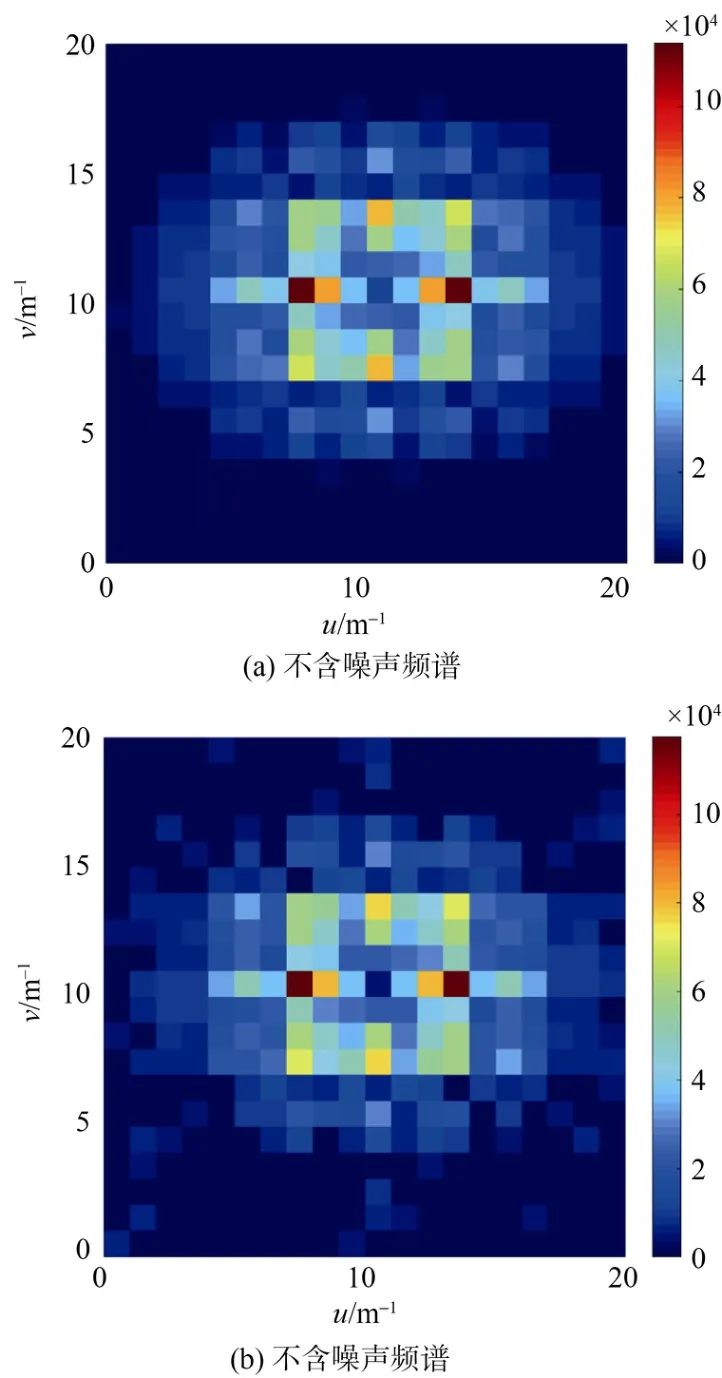
图5 磁梯度数据的幅度谱Fig.5 Amplitude spectrum of magnetic gradient data

采用第2章提出的自适应滤波方法对图4（b）所示的含噪声信号进行相关成像，图6显示了成像结果。其中：图6（a）与6（b）为Y=1.6 m处的剖面图，图6（c）与6（d）为X=1.4 m处的剖面图，图6（a）与6（c）为采用了所提滤波方法的结果，图6（b）与6（d）为未采用滤波处理的结果。图中黑色方框代表实际模型的位置，白色十字符号代表相关系数的极大值位置。可以发现，经过滤波处理后，相关系数的极大值位置与模型的中心位置基本重合，只有图6（c）中模型3在Z方向有0.05 m误差；无滤波处理的成像结果中，如图6（b），模型2在X和Z方向均有0.05 m误差；图6（d）中，模型3在Z方向均误差0.1 m。

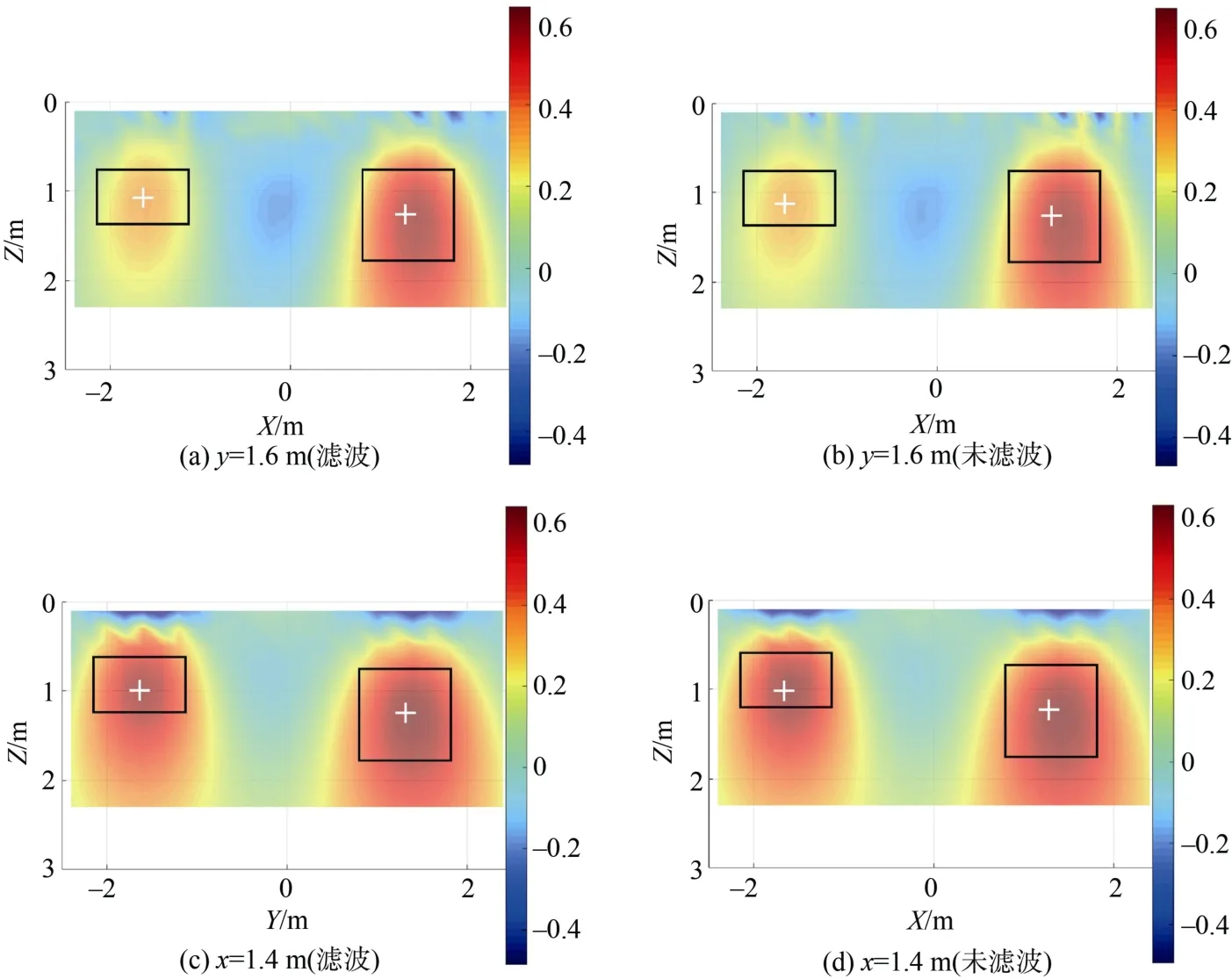
图6 相关成像结果Fig.6 The correlation imaging results

由于实际应用中需要通过相关系数的极大值位置估计磁性体中心的位置。用上述2种方法估计出4个模型的中心位置如表2所示。

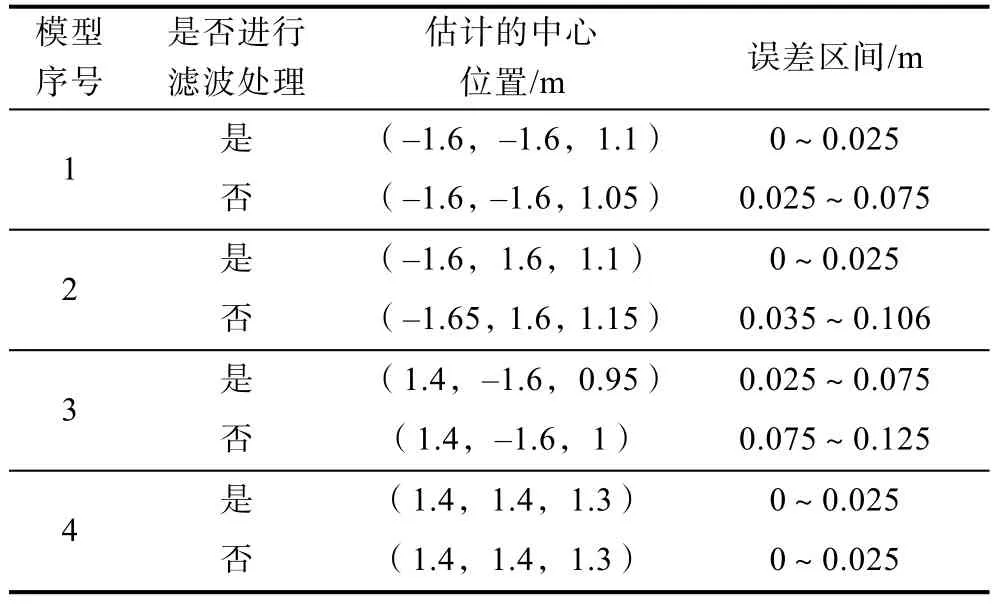
表2 根据成像结果估计的模型中心位置Table 2 Estimated center position of model based on imaging results

由于相关成像方法需要将未知空间离散化为有限个网格，因此当估计的模型中心位置与实际位置一致时，并不代表误差为0。如表2中的模型1，估计的中心位置是（–1.6，–1.6，1.1），表明模型中心位于以（–1.6，–1.6，1.1）为中心，边长为0.05 m的一个正方体网格内，误差区间为0～0.025 m。表2中各个模型的中心位置误差范围表明，提出的滤波方法对误差有明显改善，最多减小了1–0.25/1.06≈76%的误差。

为了验证低信噪比下所提滤波方法的效果，在理论信号中加入10%的高斯噪声（如图7所示）。由于每次实验的高斯噪声是随机产生的，且10%的高斯噪声随机性已经很大，分别在有无滤波处理的条件下进行了5次实验，计算出磁性体位置误差的平均值如表3所示。

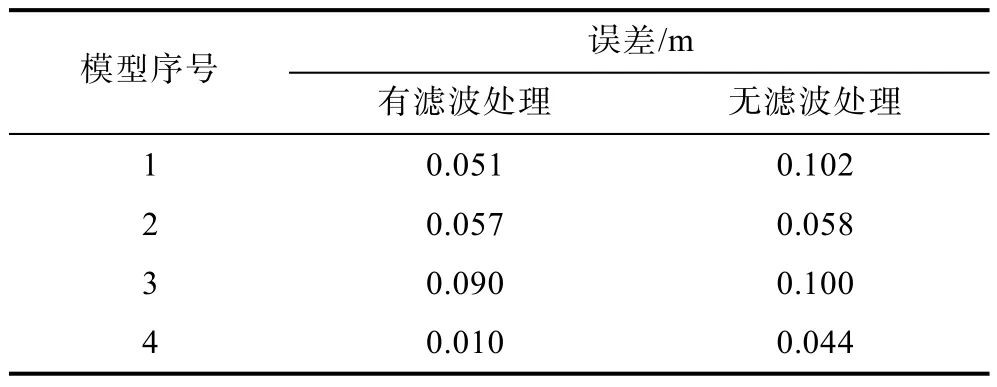
表3 低信噪比下模型位置误差Table 3 Model position errors under low SNR

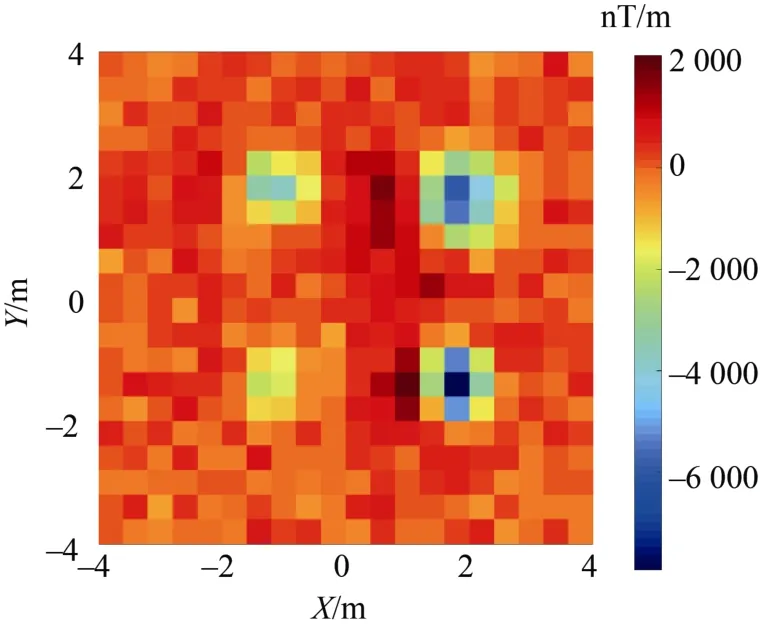
图7 含10%噪声的磁梯度数据Fig.7 Magnetic gradient data with 10% noise

根据表3，滤波处理后模型1和4的位置误差明显小于无滤波处理的结果，而模型2和3的误差没有太大变化。原因可能是相关成像算法将磁性体等效为了球形的磁偶极子，模型2和3为长方体，用磁偶极子近似会有较大误差，而模型1和4为正方体，更接近球形的磁偶极子。说明在低信噪比的情形下，滤波处理后对近似球形的模型定位结果更准确。

在表1的基础上将4个模型的深度增加0.6 m，并与图4（b）所示信号一样添加2%的高斯噪声，对含噪声信号进行相关成像以估计模型的中心位置，结果如表4所示。由于在成像结果X、Y、Z方向上均出现较多误差，因此计算出3个方向上的误差对结果进行评估。需要注意的是，表4中的模型在某一方向上的误差值为0也不代表没有误差，而是理解成与表2一样的误差区间。

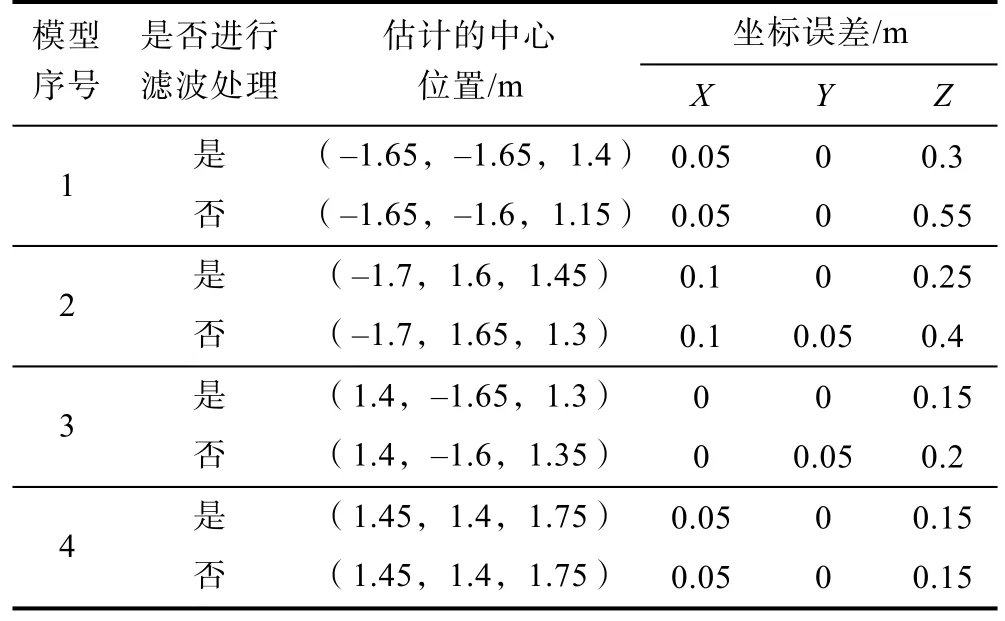
表4 模型加深后根据成像结果估计的模型中心位置Table 4 Center position of model estimated based on imaging results after deepening model

当磁性体所处位置加深后，2种方法得到的结果均向上偏移，在Z方向上误差较大，最高分别达到0.3 m和0.55 m，在水平方向上也都出现了0.05～0.1 m的误差。说明在磁性体深度较深的情况下，本文所提滤波方法对成像效果的提升已不明显，但相对未采用滤波处理的成像结果来说还是更接近真实情况。

4 结束语

针对磁梯度数据的相关成像方法纵向分辨率不足的问题，提出了一种自适应滤波方法，根据不同深度磁性体的磁梯度数据频谱差异使用不同的滤波阈值。仿真模型实验表明，在平均深度1.1 m时，滤波处理后的成像结果能较为准确反映磁性体的中心位置，有效减小了磁性体的定位误差，最多可以减小76%；在平均深度1.7 m时，深度方向上最大误差0.3 m，约为无滤波处理结果的54%；而且在低信噪比下，滤波方法还能减小近似球形的模型的定位误差。总体而言，自适应滤波可以提升相关成像法准确定位磁性体的能力。