面向水下无线传感器网络的介电弹性体能量收集技术研究
樊 鹏,朱子才,胡 桥
(西安交通大学,陕西 西安 710049)
0 引言
水下无线传感器网络是一种由水下传感器节点、水面基站和岸基中心等组成的水域监测网络系统,在海洋资源勘探、海洋灾害预警、海洋权益维护和海洋安全防御等多个领域中发挥着重要作用[1]。通过大量分布的传感器可以实时感知诸如盐度、温度、酸碱度、压力和波浪等海洋参数,从而了解水下环境和水下目标等相关信息[2]。然而,水下传感器通常采用蓄电池进行供电,需要不断地进行充电和更换,而且水下环境的特殊性使其困难性进一步加剧,导致其维护成本高昂,若不加充电或更换,则其能量资源有限、持续工作能力不足。
为了降低水下传感器的维护成本高同时延长其持续工作能力,需要对其进行原位供电。海洋中蕴藏有储量巨大的可再生能源,包括潮汐能、波浪能、海流能、温差能和盐差能等,其中海流能与波浪能因其具有分布范围广、能量密度高等特点,有望成为水下传感器的主要能量来源[3]。目前,根据发电原理的差异,水下能量收集技术主要可以分为电磁式[4]、压电式[5]、摩擦电式[6]、以及介电弹性体发电机(Dielectric Elastomer Generator,DEG)[7]。与其它水下能量收集技术相比,DEG具有功率密度(能量密度)高、变形大、疲劳寿命高、以及适用于低频带等优质特性[8],适合于收集波浪能和海流能为水下传感器原位供电。
DEG通常是一种类似于三明治的多层结构,由柔性的介电弹性体(Dielectric Elastomer,DE)芯层材料和覆盖在芯层上下表面的柔性电极材料组成。自从2001年PELRINE等人[8]首先提出基于DE的发电模式,并开发了鞋跟DEG用于收集人体运动的动能,之后由于其优异特性,被应用于收集海洋能。CHIBA等人首次在实验室环境下成功演示了基于DE的波浪能发电器的能量收集,并在实际海况下测试了安装于浮标上的DE波浪发电器,在偏置电压为2 000 V时,收集的电能平均功率为0.25 W[9-10]。JEAN等人[11]在真实海况下对基于DE的驻波管波浪能量收集装置进行研究,发现在偏置电压为2 200 V时,其平均功率为0.45 W,最大的功率为2 W。MORETTI等人[12]提出了基于膨胀圆形薄膜DEG(Inflated Circular Diaphragm DEG,ICD-DEG)的振荡水柱波浪能量收集装置,并进行了实验研究,获得的最大功率为76.8 mW,并在真实海况下对其能量收集性能进行了测试。MORETTI等人[13]也提出了基于平行四边形形状的DEG(Parallelogram-Shaped DEG,PS-DEG)的波浪能量收集装置。到目前为止,已有多款收集波浪能的DEG被报道,其具有结构简单、使用方便、价格低廉等优点,且其相关的研究主要集中于外界刺激(浪高和波长)对DEG能量收集性能的影响,而缺少对DEG自身能量收集方案的优化设计。为了进一步提高DEG能量收集的性能,本文在考虑了DE材料自身粘弹性和漏电特性的基础上,对DEG自身能量收集方案进行了优化设计提高其自身性能,以便促进面向水下无线传感器网络供电的DE能量收集技术的发展。
1 DEG理论模型
如图1(a)所示,处于未变形状态的圆形DEG的初始尺寸为半径r和厚度h。这里假定DE膜是不可压缩的。在名义等双轴应力s和电压Ф作用后,DEG的2个电极均获得电量Q(极性相反),同时DEG的尺寸变为半径λr和厚度λ–2h,且沿着厚度方向引起漏电流ileak,如图1(b)所示,λ表示DEG的面内整体拉伸比。作为一类高分子聚合物,DE材料必然具有粘弹性,本文采用粘弹流变模型[14-16](如图1(c))来描述DE材料的粘弹特性。

图1 DEG示意图Fig.1 Sketch of DEG
该流变模型由2个并列的单元组成:单元Ⅰ为1个变形可逆的超弹性弹簧α;单元Ⅱ由另一个变形可逆的超弹性弹簧β和1个粘壶串联而成。根据相应的几何关系,弹簧α变形的拉伸比为λ。弹簧β变形的拉伸比可以表示为λi=λ/ξ。其中,ξ表示粘壶的非弹性拉伸比。为了描述DE材料的应变刚化效应和有限变形行为特性,采用Gent模型[17]来表征单元Ⅰ和Ⅱ的应变能。在此基础上,可以获得粘弹性DEG的本构方程[14,18]如下
式中:ε0为真空介电常数;εr为DE材料的相对介电常数;μα为弹簧α的剪切模量;μβ为弹簧的β剪切模量;Jα为弹簧α的变形极限常数;Jβ为弹簧β的变形极限常数。另外,定义材料参数χ=μα/μ,表示不具有时间效应的聚合物网络所占的比重,用于表征材料的粘弹性[19]。随着χ的增大,材料粘性减小,弹性增大,μ=μα+μβ表示DE材料的瞬时剪切模量。
流变模型中的粘壶可以被看作为牛顿流体来建模[15],在方向 1 和方向 2,其变形率分别为ξ-1dξ/dt,与其应力的关系如下:
式中:η为粘壶的粘度;粘弹松弛时间被定义为tv=η/μβ。
如图2(a)所示,能量收集方案选取矩形收集方案[14],相应的能量收集电路如图2(b)所示。图2(c)表示外界激励的位移随时间的变化,图2(d)表示DEG的拉伸比随时间的变化。在图2(c)中,参数T表示外界激励的循环周期,也等于DEG的循环周期,位移增加阶段的时间是Td,下降阶段的时间是T–Td。定义参数时间比K=Td/T,表示一个循环周期中位移增加阶段的时间占比。

图2 DEG矩形能量收集Fig.2 Rectangle harvesting scheme of DEG
由于DE是不完美的绝缘体,因而感应电场会引起沿着厚度方向的漏电流[16]。通过将DEG表征为一个电容并联一个电阻来对漏电流进行建模(见图2(b))。因此,与DEG电极相连的导线中的电流i可以被表达为
式中:C为DEG的电容,其表达式为C=ε0εrπr2h–1λ4,漏电流ileak可以表示为[16]
式中:σc0为低电场强度下DE材料的电导率;EB为经验常数;E为电场强度,其表达式为E=Фλ2/h。
矩形收集方案的实施过程总结如下。DEG处于状态O时,其位移最小为ymin,对应的预拉伸比为λpre。然后,随着位移从ymin增大到ymax,DEG从预拉伸比λpre被拉伸到最大拉伸比λmax。当DEG处于拉伸过程O–B,DEG在恒定电压下充电至ФL,其变形速率为vs=(λmax–λpre)/Td。达到状态B后,DEG充电结束。随着位移的减小,施加在DEG上的拉伸力减小,DEG开始松弛,拉伸比减小,其变形速率为vr=(λpre–λmax)/(T–Td)。随着拉伸比的减小,电极间的电压增大。当电极之间的电压增加到ФH(状态C),稳压二极管DH反向击穿。随着位移持续减小,DEG进一步松弛,而电极之间的电压保持不变。当vr较大时,由于材料的粘性,可能出现在位移减小到ymin之前拉力降至0的现象(这种现象已经在文献[21]的实验中观察到),这会导致DEG可以松弛到的最小拉伸比λmin大于λpre,即DEG不能恢复到初始位置。这种情况由图2(a)中的循环D-A-B-C-D表示。当vr较小,随着位移减小到ymin,由于拉力大于0,DEG可以返回到初始位置[21],图3(a)中循环E-F-B-C-E表示这种情况。对于循环D-A-B-C-D而言,当DEG松弛到状态P时,拉力减小到0,然后继续松弛,直到达到状态D,因此,其松弛过程包括非自由松弛阶段B-P(拉力大于0)和自由松弛阶段P-D(拉力等于0)。而在循环E-F-B-C-E中,松弛过程只包括非自由松弛过程B-E。当DEG处于自由松弛过程时,DEG的变形率可以表示为[22-23]
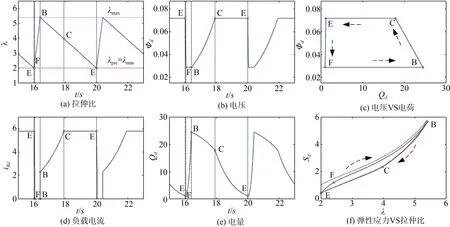
图3 在输出端接入负载电阻R=500 MΩ且K=0.1时DEG的动态响应Fig.3 Dynamic response of DEG at R=500 MΩ and K=0.9
式中:Gλ和Gξ两者可以被表达为
为了能够表征在一个能量收集循环中DEG的能量收集性能,引入如下参数:漏电流耗散的能量Wleak、能量密度Edensity、输入的机械能Wmech和机电转换效率ηc。当图2(b)中输出端接入负载电阻R时,引入另外2个参数:负载耗能PR和电源管理效率ηpm,其中,对参数Wleak、Edensity,PR和Wmech进行无量纲化处理如下:
2 DEG动态行为特性
在构建的DEG理论模型基础上,进一步研究时间比K和负载电阻R对矩形收集方案下DEG的动态相应特性的影响,以便更好地理解DEG的力学和电学参数的变化,并为后续通过调整时间比来优化能量收集方案以及匹配合适负载提供助力。选取DEG的参数为μ=600 kPa,χ=0.5,Jα=110,Jβ=55,εr=3.5,tv=1s,ε0=8.85×10–12F/m,EB=40 MV/m,σc0=3.23×10–14S/m,ФH=5 kV,ФL=2 kV,f=0.25 Hz,r=20 mm,h=0.5 mm,λpre=2和λmax=5.4[14,16,19,20,24]。为了便于比较分析,对参数进行无量纲处理如下:无量纲电压,无量纲电荷,无量纲应力sd=sμ,流经负载的无量纲电流,其中,iR表示流经负载R的电流。
图3描述了当输出端接入负载电阻R=500 MΩ且时间比K=0.1时DEG的动态响应。由图3(a)可见,DEG的拉伸比可以减小到初始预拉伸比(状态E)。而且,在整个循环E-F-B-C-F中都保持应力大于0(见图3(f)),表明DEG不会经历自由松弛过程。图3(d)描述了处于稳定状态下的DEG流向负载电阻R的电流变化。当DEG松弛到状态B时,开始对负载电阻进行供电。随着电压的升高,负载电阻的电流iRd持续增加到状态C。然后,由于恒定的高电压ФH,电流iRd也保持恒定,直到松弛过程结束(在状态E)。在DEG达到状态E之后,仍有DEG残余的电荷流过负载电阻,直到电压降低到ФL。由图3(c)、(e)可见,由于部分电荷被负载电阻耗散,状态C的电荷会显著低于状态B。在这种情况下,DEG可以返回到初始位置,仅仅经历非自由松弛过程,且在该过程中保持高电压ФH。
图4展示了当输出端接入负载电阻R=500 MΩ且时间比K=0.9时DEG的动态响应。由图4(a)可见,在状态D,λmin>λpre,表明DEG不能返回初始位置。另外,从图4(f)可见,DEG会经历自由松弛阶段PD。但是,在整个阶段PD、DEG不能够一直保持高电压ФH(见图4(b)、(c)),相应地,流过负载电阻的电流也不会保持恒定(见图4(d))。另外,在DEG达到状态G后,其电压和通过负载电阻的电流都会开始降低。其主要原因是DEG上电荷的变化率不能同时满足高电压下的漏电流和通过负载电阻的电流。在此种情况下,DEG不能够返回到初始位置,并经历自由松弛过程,且在该过程中不能够持续保持高电压ФH。

图4 在输出端接入负载电阻R=500 MΩ且K=0.9时DEG的动态响应Fig.4 Dynamic response of DEG at R=500 MΩ and K=0.9
图5展示了当输出端接入负载电阻R=100 MΩ且时间比K=0.1时DEG的动态响应。如图5(a)所示,DEG的拉伸比可以减小到λpre。由图5(f)可知,阶段BE为非自由松弛过程,因此,DEG不会经历自由松弛过程。如图5(b)、(c)所示,在一个周期中电压的曲线类似于一个半正弦波的冲击脉冲信号,其峰值低于高电压ФH。另外,也可以看出,在DEG松弛初始预拉伸比之前,其电压已经降低到低电压ФL(状态E)。这主要是由于处于松弛过程的DEG的负载电阻小且变形速率低。尽管在阶段EF,DEG处于低电压,DEG仍然向负载电阻供电(如图5(d)所示)。此种情况下,DEG可以返回到初始位置,在此位置DEG处于低电压ФL,仅仅经历非自有松弛过程,且在该过程中其电压不能升高到高电压ФH。
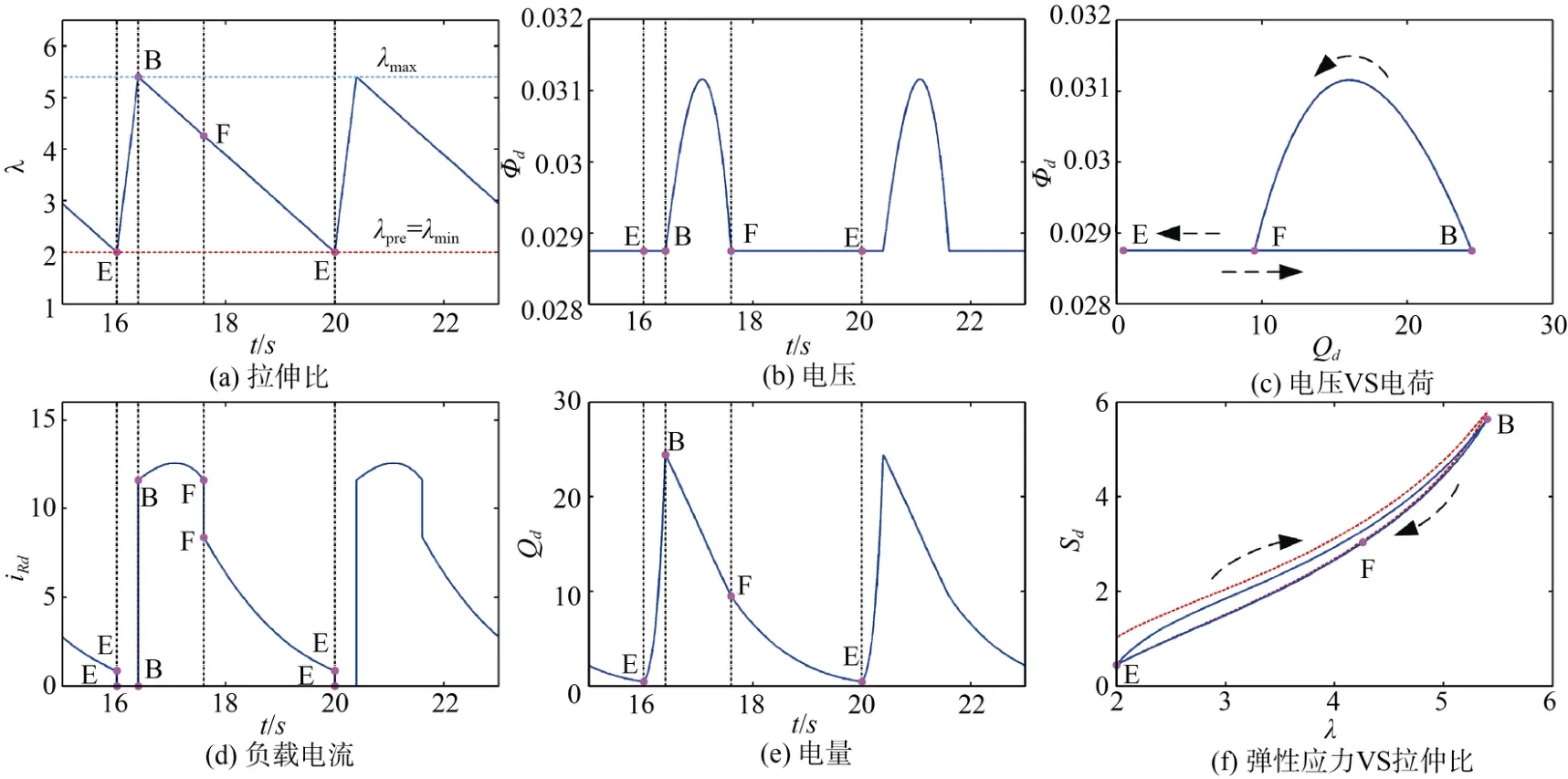
图5 在输出端接入负载电阻R=100 MΩ且K=0.1时DEG的动态响应Fig.5 Dynamic response of DEG at R=100 MΩ and K=0.1
图6展示了当输出端接入负载电阻R=25 MΩ且时间比K=0.9时DEG的动态响应。如图6(a)、(f)所示,DEG的松弛过程包括非自由松弛过程(阶段BP)和自由松弛过程(阶段PD),且λmin>λpre,因此,DEG不能返回初始位置。在松弛过程中,电压的曲线形成半正弦波的冲击脉冲,其峰值低于高电压ФH(见图6(b))。从图6(b)可见,在DEG应力减小到0(状态P)之前,其电压已降低至低电压ФL(状态A),表明在非自由松弛过程中电压已经降低至ФL。在整个松弛过程中,DEG可以为负载电阻供电,如图6(d)所示。在此种情况下,DEG不能返回到初始位置,且会经历自由松弛过程和非自由松弛过程,在自由松弛过程中,DEG处于低电压ФL,同时,在非自由松弛过程中,DEG不能升高到高电压ФH。
3 DEG能量收集性能
在研究了DEG的动态特性后,进一步研究时间比K和负载电阻R对采用矩形收集方案的DEG的能量收集性能的影响,以便能够优化能量收集方案提高能量收集性能。正如前文所述,性能参数主要包括漏电流耗散的能量Wleak、能量密度Edensity、输入的机械能Wmech、机电转换效率ηc、负载耗能PR和电源管理效率ηpm。
图7展示了在不同的负载电阻R下时间比K对DEG的能量收集性能的影响。如图7所示,当负载电阻较小,例如R=25 MΩ和100 MΩ,如果时间比K低于某个临界值(图7中采用“×”表示),DEG将不会产生电能,反而会浪费。由图7(a)可见,当较大的负载电阻被供电,例如R=500 MΩ,随着时间比K增大,漏电流耗散的能量Wleak会增加。当负载电阻减小到100 MΩ和50 MΩ,Wleak随K的变化呈现出先增大后减小的变化趋势。原因如下,当K较小时,在松弛过程中DEG的电压不能升高到高电压ФH。随着K增大,电压峰值增大,导致漏电流增大,因而漏电流耗散的能量Wleak会增加。当K较大时,DEG的电压可以升高到ФH,随着K增大。处于高压ФH的时间减少,因而漏电流耗散的能量Wleak会减小。当负载电阻进一步减小到R=25 MΩ时,Wleak随K的增大而增大。这是由于负载较小时,DEG的电压不能升高到ФH,而随着K增大,电压峰值增大,Wleak也会增大。从图7(a)也可见,Wleak随R的增大而增大。主要原因如下:随着R的增大,DEG的电压的峰值增大(DEG电压未达到ФH),或者处于高压ФH的时间延长(DEG电压达到ФH),因而漏电流耗散的能量Wleak会增大。
如图7(b)所示,增大时间比K和电阻R均可以提高DEG的能量密度。其原因如下:当K或者R增大时,DEG的电压峰值增大(DEG电压未达到ФH),或者其电压升高到高压ФH时的电量(见图3状态C)增多,导致在电压–电量平面内DEG稳态时封闭曲线围成的面积增大(见图3)。因此,DEG收集的能量增加。由图7(c)所示,当R较大时,输入的机械能Wmech随K的变化是非单调的,当R较小时,随着K的增大,Wmech也增大。如图7(d)所示,在R=500 MΩ,随着K的增大,机电转换效率ηc会先增大后减小,而在R=100 MΩ,50 MΩ和25 MΩ,ηc会随着K的增大而增大。另外,从图7(d)可见,增大负载电阻也可以提高机电转换效率。
图7(e)描述了在不同负载电阻R下时间比K对负载耗散的能量PR的影响。从图7(e)可见,在R=500 MΩ,增大K会减小PR。对于较大的负载电阻R,DEG的电压可以升高到高电压ФH,因而,PR主要由处于高电压ФH的时间所决定。所以,随着K的增大,DEG处于高电压ФH的时间缩短,PR减小。当负载电阻R减小到100 MΩ和50 MΩ,随着K的增大,PR会先增大后减小。主要原因如下:正如前文所述,较小的K,DEG的电压不能升高到高电压ФH,其电压峰值会随着K的增大而增大,导致PR增大,而较大的K,DEG可以升高到ФH,因此,随着K增大,PR减小。当R进一步减小到25 MΩ,PR会随K的增大而增大,这主要是由于R较小时,DEG不能升高到高电压ФH。
图7(f)描述了在不同负载电阻R下时间比K对其电源管理效率ηpm的影响。在R=500 MΩ,减小时间比K可以提高ηpm。当R减小到100 MΩ和50 MΩ,随着K的增大,ηpm会先保持恒定然后减小。当R进一步减小到25 MΩ,ηpm保持恒定。其原因如下:当DEG的电压可以升高到高压ФH,随着K的增大,Edensity会增大而PR会减小,则ηpm会减小,而如果DEG不能升高到ФH,则其全部收集到的电能被用于为负载电阻供电,因此,ηpm会保持恒定为100%。
4 结束语
针对水下无线传感器网络的DE能量收集技术存在能量收集性能低的问题,在考虑DE材料粘弹性和漏电特性的基础上,本文构建了矩形能量收集方案下可以表征自由松弛过程的DEG理论分析模型。在此基础上,研究了在不同负载电阻和外界激励位移增加阶段占整个周期的时间比,DEG的动态响应和能量收集性能。主要结论如下:1)增大负载电阻或时间比,可以提高DEG的能量密度;2)当负载电阻较大时,存在一个最优的时间比使机电转换效率最高,而在负载电阻较小时,增大时间比可以提高机电转换效率,另外,增大负载电阻可以提高机电转换效率;3)在较大负载时,增大时间比可以减小负载的能耗,而在较小负载时,增大时间比则会提高负载的能耗。另外,当负载处于中间值时,负载的能耗随时间比的变化是非线性的。需要指出的是,本文通过理论研究给出了DEG的优化设计措施,后续需要研究人员在实验室以及真实的海洋环境下对该优化措施进行验证和修正,并针对粘弹性对DEG能量收集性能的影响开展研究。综上,本文为面向水下无线传感器网络的DE能量收集技术的性能优化提供了新的解决途径。

