借“数直线”之形 促概念深度建构——以“在直线上表示分数”为例

文|魏燕红

数轴是小学课堂常用的基本的数学工具之一。小学数学教学中并没有揭示数轴的概念，而是以“数直线”这一方式加以替代。“数直线”作为一种数形结合的学习工具，是带给学生解决问题的方法和思路最直观而有效的方式。在数的认识教学中灵活应用“数直线”，能起到化繁为简、事半功倍的效果。

教材在分数教学中编排“数直线”，其编排意图十分明显，教材中的每一条数直线都承载着提升学生数学思维的作用。教师要充分挖掘数直线的使用价值，将数直线这一工具有意识地向学生逐步渗透，帮助学生建构认知，提升品质。

一、“1”“1”对应，开拓思维，正确理解数直线上的“单位”

单位“1”和分数单位，“单位”是认识分数的核心词，单位的重要作用体现在能计量上。在数直线上表示分数，最关键的就是找到数直线中的单位“1”。因此，在教学中帮助学生理解单位“1”或分数单位在数直线上的表示方法，让学生经历分数先分后数的过程，是策略的核心。

1.沟通各类分数模型，正确认识数直线上的单位“1”

生活中一个图形、一个物体、一个整体都可以看作单位“1”，在数直线上的单位“1”是舍弃了生活中形形色色的事物非本质属性后高度抽象的结果，各种各样的单位“1”在数直线上都只是0 到1这一段。更明确地说，在数直线上，单位“1”只有一个，具有唯一性，否则就会与一一对应的法则冲突，从而产生混乱。

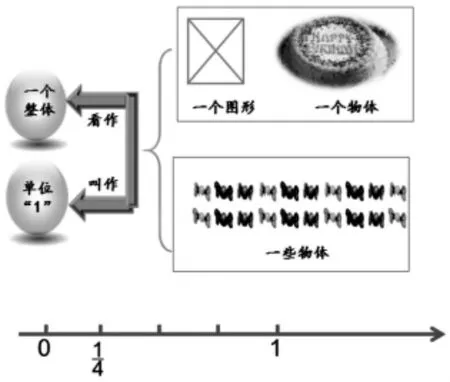
教学中第一次使用应该出现在分数的意义第二课时，在图画写出分数说出意义的基础上，通过对图中的实物模型（一个蛋糕）、面积模型（一个图形）、集合模型（20 颗糖）等抽象，让学生概括出可以看作一个整体用自然数1 来表示，对应到数直线上的“1”，将学生的认识扩展到数直线上的1，能涵盖的是生活中所有可以用“1”表示的事物，进一步让学生明晰，生活中众多的“1”都可以用数直线上的0 到1 这一段统一的单位长度来表示，可以把它们统称为单位“1”。数直线上也可以表示各种分数，比如。把数直线上0～1 这段看作单位1，平均分成4 份，一份就是可以用数直线上的这个点表示。同理也可以找到

2.先分后数，体验分数单位的计量过程，理解本质

分数是先分后数的一个数，单位“1”平均分成了几份，其中的一份就是分数单位。数直线上的分数直观地展现了分数单位的计量功能，先分知道了是什么分数单位，再数才知道有几个这样的分数单位，就是几分之几。教学中要注意引导学生先确定分数单位，再根据分数单位的累加功能寻找到分数在数直线上的对应点。

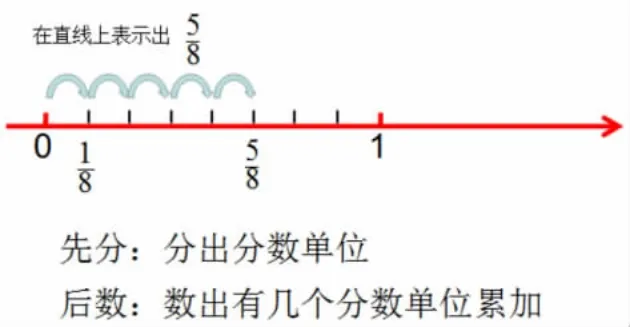
3.经历单位累加，动态演绎区间定位

突出0～1 和1～2 区间的衔接。分数超过1，标在什么位置，是在数直线上表示分数的困难所在。突破这个难点，一定要突出“0～1”“1～2”之间的衔接。这个衔接延伸的过程是教学真分数和假分数的最直观的载体。

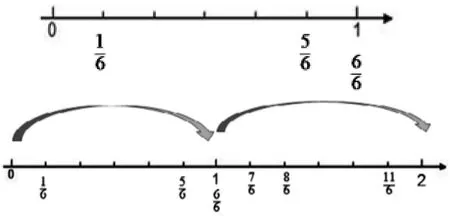
在学习《真分数和假分数》时，先出示0～1 的数直线，标出，接下去表示出，然后问这个点应该在哪里？学生能找到就是1 的位置，1 后面还有分数吗？再继续问在哪里？给学生思考的空间，经历把目光从0～1的区间跨越到1～2 这个区间的过程，动态演绎数直线向右延伸的过程。两个单位“1”累加，就是2，用自然数2 表示。思考：为什么在1 的位置，而必须在1～2 这个区间呢？学生会知道它比多一个分数单位，应该在，也就是1 的右边一个分数单位的位置。再找出和。

这里有两个目的：一是在数直线上找分数，亲身经历把数直线从一个单位延长到两个单位、三个单位；二是随着数直线的延长，丰富分数的范围，为分数的分类做好铺垫。

理解数直线上的整数是单位“1”的累加。在数直线上不仅分数单位可以累加，单位“1”也可以累加。两个单位“1”累加，就用相应的整数2 表示，以此类推。数直线上相应的整数就是单位“1”的相应的累积，经历数直线上的单位“1”的计量过程，沟通有几个单位“1”就与数直线上整数几对应，真正夯实学生对于数直线上的单位“1”的本质理解。

学了假分数和带分数、整数的互化之后，我们可以引导学生先把假分数化为带分数再来看。

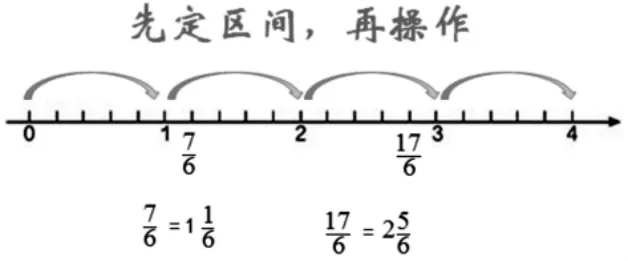
通过让学生经历0～1 与1～2的衔接过程，养成把分数按所在区间进行分类的习惯，一连串的强化训练后就能突破难点，从而有效降低错误率。

4.借助等价分数，化繁为简

例如：学习分数的基本性质之后，有这样一道习题：

二、挖掘内涵，凸显价值，构建数的集合

1.以数直线强化分数的意义在“数”上的拓展

分数既可以表示两个量之间的关系，同时也可以表示一个具体的数值。我们需要帮助学生体验分数的稠密性。

教师出示几个真分数，上面这些分数分别是将单位“1”平均分成几份，表示这样的几份，你能在数直线上找出这些分数的位置，并和大家说说你是怎么想的吗？学生在说的过程中，课件出示这些分数对应的点，适时追问：在这条数直线上，除刚才这些分数以外，你还能找到其他的分数吗？说说这个分数的含义并找到数直线上的大致位置范围，像这样的分数你找得完吗？

通过以上的活动延伸，就可以让学生比较深入地感知分数的稠密性，体验分数的无限延伸。每个分数在数直线上都有相对应的点，学生对分数的认识，最初局限在0 到1 之间，在学生建立分数概念时，需要将学生的思维进行适当的拓展延伸。

学生根据以前的学习探究，已经能把真分数与数直线上的点进行一一对应了，但是由于学生之前没有接触过假分数，因此存在思维定势。教学中凭借数直线无限延伸的特征，让学生及时打破思维定势，凭着整数和小数的学习经验引导学生进行知识迁移，感知在1 后面还有无限多个分数，并且这些分数都比1 大。通过这个过程也可以让学生更好地理解整数、分数、小数的联系。

2.在数直线上感受累加思想，建构分数集合

人教版教材提供《真分数和假分数》的例题，从圆形的分割引导学生认识真分数、假分数以及带分数。在学习的过程中，无论从假分数的出现，假分数的理解，带分数的引入以及分数的分类，数直线都要比圆形面积分割更直观、更自然。数直线是从原点出发向一个方向不断增加或减少的，这个过程能让学生体会并最大限度地感受累加的思想。所以我们把例题的思维载体改成数直线，为学生分数集合的建构提供更适合的思维支撑。

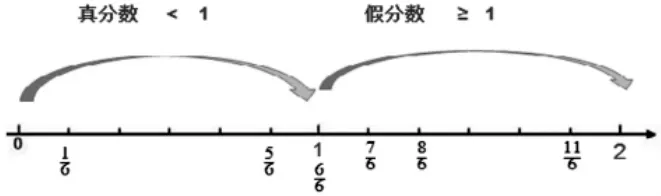
在多次试教中采用数直线作为学习材料，提供图形表象支撑，并让学生充分感受分数单位累加过程。学生不仅能很快找到分数单位，而且能在找的过程中真实地感受到假分数比1 大，位于1的右边, 对建立假分数大于等于1 的表象，起到了形象支撑的作用。同时也让学生直观地感知到，分数以1 为分界线，分为两大类：小于1 的是真分数，大于等于1 的是假分数，从而正确构建分数集合。

3.沟通数系之间的联系，形成整体认知结构

（1）形成分数和整数序列，顺应认知结构

课本中在直线上面填假分数，下面填带分数的练习。

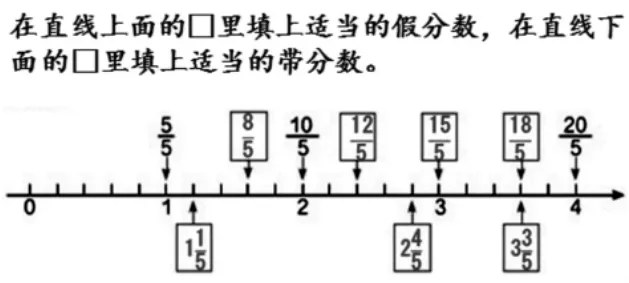
通过练习引导学生观察发现，分子是分母的倍数的分数能化成整数，相邻两个整数之间再平均分可以细分出分数，而且存在无数种分法，感悟在相邻两个整数之间有无数个分数，实现分数意义的本质建构，把分数作为新数填充在整数之间，形成分数和整数的序列，学生的认知结构通过顺应达到新的平衡。

（2）沟通整数、小数、分数之间的联系，完善认知结构

数直线的形象支撑，可以帮助学生理清各种数概念的意义、计数方法、表示方法和分类等，进行比较思辨。整数的基本计数单位是自然数1，整数其他计数单位按十进制的规则生成。而分数是先确定单位“1”，再根据平均分的份数确定分数单位，平均分的份数不同，分数单位也不同。数直线借助图形表征数概念，丰富学生对数的形象感知，引导学生在整体建构层面上理解和把握数的概念，进一步完善认知结构。

我们要深入理解数直线的内涵，挖掘其教学价值，拓展其应用范围，发挥数直线的作用与功能，帮助学生建立大数学观，培养学生的数学素养。