桥梁结构动挠度变化规律及计算模型研究

黄晓东

(中国华西工程设计建设有限公司,四川 成都 610000)

0 引言

桥梁工程在建设过程中,需对桥梁主体结构进行受力分析,具有评定桥梁受力状态是否满足安全性及可靠性的要求。车辆移动荷载是检验桥梁变形稳定性的重要检验标准,因此,车辆动荷载的挠度变化规律是掌握桥梁受车辆动载影响的关键所在。

由于桥梁受动荷载的影响较大,容易出现偏移量大、沉降开裂以及失稳等情况,大量学者对桥梁动荷载的研究非常重视。史大利[1]通过车辆移动荷载的跑车、刹车及跳车等对预应力混凝土连续刚构桥动力响应分析,判定桥梁动力特性是否异常;马松江[2]依托于试验检测进行桥梁动载及静载有限元模拟,并依据长期挠度观测,评价桥梁结构的安全性;张文韬[3]以桥隧结构综合体系为研究对象建立车辆移动荷载有限元模型下的结构振动响应,提出最不利位置的影响系数,并提出改进建议;潘平[4]通过收集大量桥梁动静载试验数据,对比分析桥梁动静载试验参数的潜在规律,提出经济合理的桥梁结构试验方法;姜红喜等[5]依据桥梁自振特性与车辆移动荷载的联合特性,结合试验检验结果,对桥梁的安全稳定性进行评价;王一平[6]通过某大桥的动力响应有限元分析并结合实际检验结果,获得了桥梁动力系数的变化规律。

大量研究表明,动荷载对工程中的桥梁稳定性影响较大,研究人员对此进行的理论研究仍处于探索阶段。为研究车辆移动荷载对桥梁结构挠度变化的规律,本文依托于某工程箱型桥梁的结构特点,施加不同车速、不同轴重的车辆移动荷载,分析桥梁的挠度变化规律,获得动挠度随车速及轴重变化的计算参数拟合结果。

1 桥梁动载分析理论

1.1 有限元理论概述

有限元计算方法在土木工程的力学计算中得到广泛应用。它是一种通过数理方法计算方程进行求解各类受力特性的分析软件,该方法主要是将数学理论与结构特性紧密结合在一起的计算方法,最终通过计算机运算获得新型数值计算技术。从有限元计算的应用上看,在电磁学、热力学、流体力学、固体力学等方面均能得到广泛的应用[7],尤其是针对结构分析,在房建工程、桥隧工程、基坑工程、边坡工程等应用较为普遍。

从20世纪50年代,有限元计算的思想初具萌芽,1943年,R.Courant首次提出截面的划分形式主要以三角形区域进行划分的概念,有限元思想最早起源于20世纪50年代,当时并没有形成一个准确的概念[8-9],1956年,Turner,Clough为研究飞机结构的平面应力受力状态,提出了三角形单元法进行计算解答的方式,并获得了精确的结果。到1960年,Clough通过论文的发表正式提出了有限元分析方法这一概念,此后,大量学者及科研人员逐渐对有限元理论进行研究分析,在20世纪80年代初期,随着计算机的普及,有限元分析方法与计算机的结合,大大加快了计算效率。

1.2 桥梁动荷载时程分析

桥梁动荷载时程分析是通过荷载与时间的依存关系,建立荷载随时间变化的受力变化规律,通过桥梁结构自身的特性及外界动荷载的影响,建立能够获得不同时刻下的受力变形响应规律。

在桥梁荷载作用的分析过程中,常见的荷载形式是以车辆动荷载施加的模式进行,由于车辆荷载通常以轮胎进行传递力到桥梁主体结构上,计算过程通常以移动的力来代替车辆荷载,以此模拟实际受力状态,最终获得桥梁承载能力的计算结果。此外,车辆荷载的施加可采用冲击系数进行简化代替,通过冲击振动作用将动载分析以静载分析的过程进行呈现。在计算机技术不断发展完善下,有限元分析软件在解决车辆动载对桥梁结构的影响分析更为便捷,由于桥梁本身的结构质量大,车辆的质量与其相比相差甚远,因此车辆与桥梁的耦合振动影响极小,可以采用简化后的动力计算模型进行代替[10]。车辆匀速荷载状态下的模拟图如图1所示,由于车辆荷载在某时刻的作用是一种瞬间加载的过程,因此在时程分析过程中可近似为三角形荷载进行模拟计算。

2 有限元模拟参数

2.1 模型参数

某桥梁为混凝土箱梁,主梁结构采用C50混凝土,长度为25 m。将全桥计算模型分11个节点,10个梁单元,桥梁截面尺寸示意图及有限元模型如图2所示,桥梁两端约束条件采用固定端约束。

2.2 加载参数

桥梁工程的结构分析过程中,为进行移动荷载的分析,应依据响应的移动荷载标准进行车道设置,为研究移动荷载的动力响应规律,本文的行车道宽度设置为3.5 m,以车道中心为基准向两侧设置1.75 m的偏向距离,并以规范(JTG B01—2003)CH-CD车辆荷载进行定义。加载单位力为1,加载系数设置为-200,则加载力值为-200 kN,方向向下。如图3所示,分析类型采用线性分析,分析方法采用振型分析法,时程类型采用瞬态分析。为研究车辆荷载作用下箱型桥梁的变化规律,本文取车速5 km/h,15 km/h,30 km/h,60 km/h,90 km/h,120 km/h及轴重50 kN,100 kN,150 kN,200 kN,250 kN,300 kN作为本文的研究对象。

3 桥梁动荷载结构受力分析

3.1 车辆动载下跨中动力响应时程分析

60 km/h车速、200 kN轴重条件下跨中的加速度及动挠度时程曲线如图4所示。

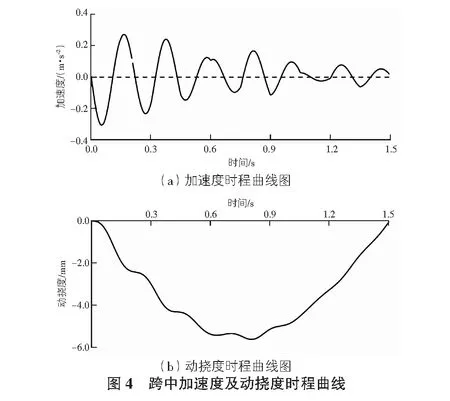
从图4(a)可以看出,箱型桥梁跨中的加速度随着时间的增加而逐渐衰减,说明桥梁在前期的震动较大,随着车辆的驶入,桥梁与车辆的共振效应逐渐减弱,直至趋于稳定状态;从图4(b)可以看出,箱型桥梁的动挠度随着时间的增加呈现先增大后减小的趋势,且在车辆到达跨中偏右0.17 m,即在0.81 s时,跨中动挠度达到最大值为-5.62 mm,此时加速度达到峰值0.167 m/s2,速度为-0.04 mm/s,速度基本趋近于0,动挠度达到峰值。

3.2 不同车速条件跨中动力响应规律

为研究不同车速的影响,选择5 km/h,15 km/h,30 km/h,60 km/h,90 km/h,120 km/h的车速进行有限元模拟计算。200 kN轴重下不同车速跨中加速度及动挠度变化规律曲线如图5所示。

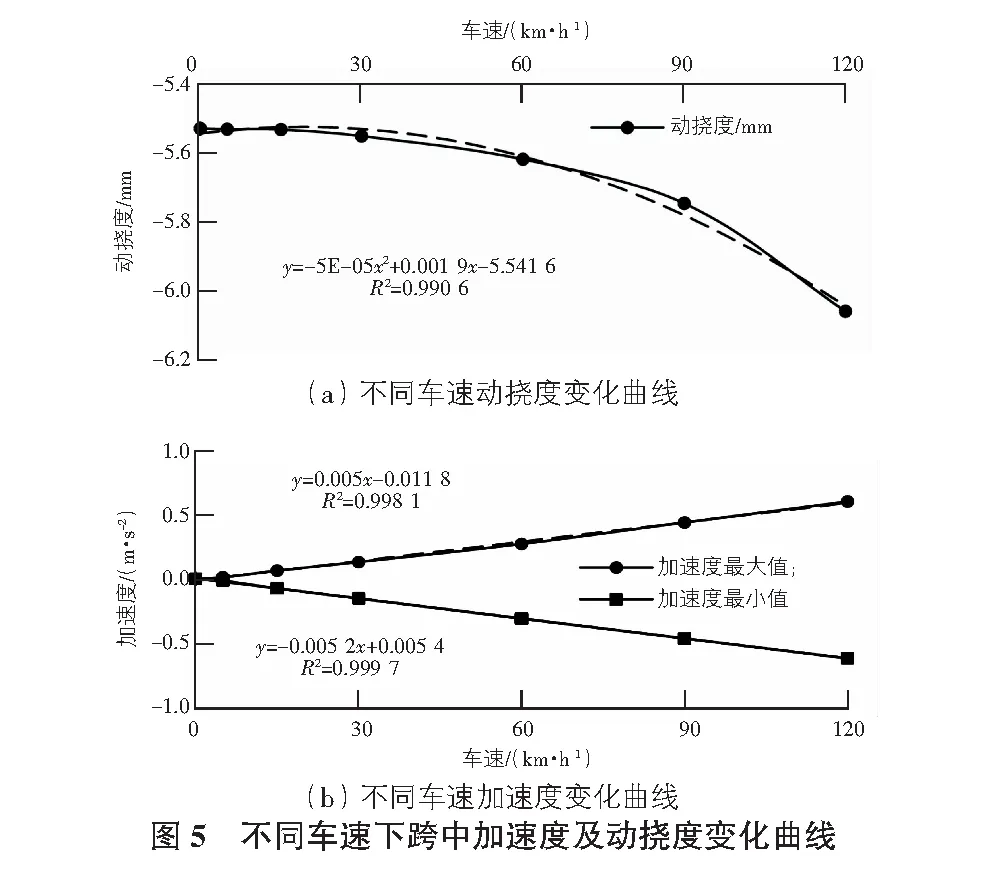
从图5(a)可以看出,在轴重恒定的条件下,随着车速的不断加快,箱型桥梁跨中的动挠度呈现先缓慢增加而后快速增加的趋势,动挠度变化速率呈现直线增加的趋势,从图中可以看出,动挠度随着车速的增加呈抛物线的形式,相关系数在0.99以上;从图5(b)可以看出,在轴重恒定的条件下,随着车速的不断加快,加速度最大值与最小值的绝对值呈现直线增加的趋势,相关系数几乎接近于1,说明车速与加速度几乎呈现正比例关系。

3.3 不同轴重条件跨中动力响应规律

为研究不同车辆轴重的影响,选择50 kN,100 kN,150 kN,200 kN,250 kN,300 kN的轴重进行有限元模拟计算。60 km/h车速下不同轴重跨中加速度及动挠度变化规律曲线如图6所示。

从图6(a)可以看出,在车速恒定的条件下,箱型桥梁跨中的动挠度随着轴重的增加,呈现线性增加的趋势,相关系数近乎为1;从图6(b)可以看出,不同轴重的加速度变化趋势与不同加速度的变化趋势呈现一致现象,均成纤维线性关系,表明加速度与轴重及加速度呈现正比例关系。

4 动挠度变化规律曲线拟合

为研究动挠度与车速及轴重的关系,首先引入静载条件下的跨中挠度公式[11](见式(1)),以此获得静载条件下的跨中挠度:

f=Fl3/(48EI)

(1)

其中,f为跨中的挠度值,mm;F为荷载,kN;l为桥梁长度;E为弹性模量,kN/mm2;I为惯性矩,mm4。

根据本文所研究的箱型桥梁计算参数及式(1)可获得,在静载状态下,200 kN的车辆荷载作用于跨中时,跨中的挠度值约为-5.528 mm。由于轴重与动挠度呈线性关系,且相关系数近乎为1,当车速不变时,动挠度与轴重呈现y=ax+b的趋势,因此,根据不同车速、不同轴重条件下拟合动挠度计算参数,获得拟合公式如式(2)所示:

fw=m·v2+n·v-Fl3/(48EI)

(2)

其中,fw为不同车速、不同轴重条件下跨中的动挠度值,mm;m,n均为拟合参数;v为车速,km/h。根据拟合结果,获得m,n的拟合参数分别为-0.000 05,0.001 8,相关性R2=0.999 7,有限元计算结果与计算拟合结果对比结果如表1,图7所示。

表1 拟合结果对比表

从表1,图7可以看出,有限元模拟值与计算参数拟合结果均在y=x附近,说明在不同车速及不同轴重条件下的动挠度计算值与有限元计算的结果规律一致,误差基本在0.1 mm以内,可信度较高,表明本文建立的参数计算模型能够很好的反映动挠度随车速及轴重的变化规律,为桥梁工程在车辆移动荷载作用下的变形趋势提供参考依据。

5 结论

本文依据某箱型桥梁工程,建立了不同车速及不同轴重条件下的有限元模型,通过分析动挠度变化规律及计算参数模型建立,获得以下结论:

1)在60 km/h车速、200 kN轴重条件下,车辆到达跨中偏右0.17 m时,跨中动挠度达到最大值为-5.62 mm,此时加速度达到峰值0.167 m/s2,速度为-0.14 mm/s,趋近于0,动挠度达到峰值。

2)随着车速的不断增加,动挠度的变化速率呈现增加的趋势,随着轴重的增加,动挠度的数值呈现线性增加的趋势;随着相同轴重不同车速、相同车速不同轴重的变化,加速度呈现线性增加的趋势。

3)本文所建立的动挠度fw计算参数模型可以用来表征不同车速及不同轴重条件下的动挠度变化规律,误差基本在0.1 mm以内,可信度较高,表明本文建立的参数计算模型能够很好的反映动挠度随车速及轴重的变化规律。