基于高效特征值分析方法的旋转失速先兆预测

徐慎忍，何晨，孙大坤，袁蔡嘉，曹东明，赵家资，王丁喜

1．西北工业大学 动力与能源学院，西安 710072

2．中国空气动力研究与发展中心，绵阳 621000

3．北京航空航天大学 能源与动力工程学院，北京 100191

旋转失速起始点决定了压气机能够稳定运行的最小流量。失速发生时，压气机中出现自激流动失稳现象，可导致气动性能恶化并诱发流致振动，造成结构破坏。因此，过去的约80 年见证了失速机理、失速预测和失速控制等方面的大量试验、理论和数值研究［1］。早期的一些试验研究中发现旋转失速发生前可在叶片前缘上游监测到幅值逐渐增加并最终导致旋转失速甚至喘振的长波扰动，这一现象后来被称为模态型旋转失速［2-4］。麻省理工学院的Greitzer 提出了可用线性失稳理论来解释旋转失速先兆扰动［5］。该理论认为，在旋转失速发生初期，压气机内流动以Hopf 分岔形式发生失稳。这一线性失稳理论定性解释了很多早期试验研究中观察到的模态型失速现象。然而在1990 年前后针对负荷更高的现代压气机的诸多试验测量中发现了一种与模态型失速截然不同的失速模式，此类失速发生时流场扰动的空间尺度远小于模态型失速且发生的时间尺度更小［6］。具体而言，在流场中产生振幅与主流相当的剧烈波动前并未监测到模态型长波扰动。由于这类失速发生时所监测到的压力脉动信号往往存在突尖波形，因此这种失速现象被称为突尖型失速。这对经典的线性失稳理论提出了挑战，因为该理论似乎无法解释突尖型失速的触发机理。

虽然学术界和工业界普遍认为突尖型失速不是由模态波引起的，然而这2 种现象并非毫无关联。剑桥大学Day 在试验中发现只要减小叶顶间隙即可实现从模态型到突尖型失速的切换［6］。由此可以猜测：突尖型失速是否亦是由模态波触发的？虽然这一猜测由于在突尖型失速试验中未观察到模态波而很早就在文献中被否定了，然而作者团队认为这一判断并无严谨的理论根据。对于在试验中未在突尖信号前发现模态波信号，并不能排除测量仪器精度有限的原因。可以想象，模态型失速中，模态波幅值增长到某临界值才会触发大规模流动失稳并导致旋转失速。该临界值与压气机的负荷水平显然具有很强的相关性。对于高负荷压气机，如果触发流场大规模失稳所需的扰动阈值小于仪器测量精度，自然就无法在所谓的突尖失速发生前监测到模态波信号［6］。与风洞试验相比，数值模拟中可通过监测某些特定位置的压力脉动来实现数值传感器的效果，其精度比物理传感器高得多。例如，对于双精度非定常RANS 求解器，10-10Pa 量级的压力脉动可以很容易被监测到，而这在试验测量中几乎不可能。因此，数值模拟方法为研究突尖型失速是否亦由模态波扰动触发提供了可能。

随着数值算法和高性能计算（High Performance Computing， HPC）硬件的快速发展，基于RANS（Reynolds Averaged Navier-Stokes）方程的计算流体力学（Computational Fluid Dynamics，CFD）方法目前已被广泛应用于压气机气动设计和分析中。在旋转失速研究中，传统测量方法时空分辨率低，而基于RANS 方程的数值模拟方法很好地克服了这一弱点。牛津大学的He 在某亚声速压气机环形叶栅［7］与He 和Ismael 在某跨声速轴流压气机［8］上的非定常模拟结果显示，非定常RANS 的CFD 手段可定性地模拟旋转失速现象。为了进一步提高分析效率，剑桥大学的Brandvik 和Pullan 开发了可在图形处理单元（Graphics Processing Unit， GPU）集群上运行的高效大规模非定常流场模拟程序TurboStream［9］，并基于此程序对NASA E3压气机中某转子和剑桥大学某低速压气机进行了非定常模拟［10］。该研究一方面如实地再现了突尖型旋转失速，提出突尖型旋转失速是由从叶尖前缘吸力面延伸到机匣上的龙卷风状涡流结构导致的；另一方面也指出突尖失速发生时伴随着叶尖区域局部冲角过大的情况，从而引发前缘流动分离。并基于此现象，进一步提出了局部冲角过大而非叶顶间隙才是发生突尖型失速的必要条件。然而，尽管使用了高效的GPU 求解器，此类高精度非定常分析的计算成本仍然极高。基于当前的高性能计算硬件资源，只能对某些特定算例的个别工况进行分析，若要将其应用于参数化研究从而确定旋转失速关键影响因素，依然显得力不从心。除高昂的计算成本外，大多数旋转失速非定常模拟都采用了增大个别叶片的安装角以人为制造叶片失谐或施加外部扰动加速触发失速的做法。这样做的目的之一是将失速发展过程控制在一段相对较短的时间内，从而降低计算成本。否则，从非定常模拟开始到突尖型失速信号出现可能需要耗费极长的时间。然而，若要彻底弄清突尖失速是否由缓慢增长的模态波增长到一定程度触发的，必须开展从稳定工况开始直到突尖失速发生之间整个物理过程的非定常模拟，并且此过程中不应引入叶片失谐或施加外界扰动，可想而知，相应的非定常模拟成本会更高。

本工作的主要目的是建立一种高效的稳定性分析方法，使其能够以远低于非定常模拟计算成本的代价研究无叶片失谐、无外部扰动时流场小扰动自发增长的过程，并基于此工具准确诊断所谓的突尖型失速是否亦由模态波触发。由于本文工作的远期目标是为了验证模态型和突尖型失速是否都由线性失稳诱发，因此可引入小扰动假设，将非定常小扰动分析转换为特征值问题，并发展适用于大规模流动问题的高效特征值分析方法。基于特征值的全局稳定性分析方法使得能够以极低的计算成本对失速前的流动失稳细节进行精细化定量研究。

特征值方法已成功应用于外流稳定性研究，尤其是针对翼型、机翼甚至整个飞行器的激波抖振现象的研究［11-12］。外流中激波边界层干扰所导致的抖振现象的根源近几十年来一直悬而未决。直到最近几年，针对其失稳机理的观点才逐渐统一，即抖振本质上是Hopf 分岔线性失稳现象。而这个观点也在时域非定常模拟［13-14］和特征值分析研究［12，15］中得以印证。与时域非定常模拟手段相比，特征值分析得到的特征值和特征向量可用于重构流场小扰动的时空演化，但其计算速度却比前者快几个数量级，并且在流场扰动增长至开始体现非线性之前能够揭示与成本极高的非定常模拟同样丰富的流动信息。此外，特征值分析结果还包含了激波抖振模态的空间结构，将其与非定常模拟结果或试验结果进行对比，也可验证计算所得特征值和特征向量的准确性。

基于特征值计算的稳定性分析方法在压气机流动稳定性研究中也已有应用。基于不可压缩、无黏和轴对称假设，通过引入忽略叶片复杂几何外形但仍保留其对流动扰动作用的叶片力模型，流动失稳问题即可转化为特征值问题［16］。类似的，北京航空航天大学孙晓峰团队通过引入浸没边界法，并分别将叶片对流动转折和黏滞的作用力视为源项代入到线化RANS 方程中，建立了基于特征值方法的可压缩流动稳定性通用理论［17］。该方法已成功应用于轴流压气机［18］和离心压气机［19］失速研究中。此外，压气机叶片前掠和后掠对于失速起始点的影响也可以通过此基于特征值的稳定性分析方法进行研究［20］。然而，需要注意的是，由于在上述研究中引入了背景流场周向均匀的假设，因此不能解析流动在周向的空间分布。事实上，只有完全基于三维流动方程的特征向量才能够为流动失稳研究提供与三维非定常流动模拟同样丰富的信息。在充分考虑叶轮机械中几何结构和流动循环对称特征的基础上，帝国理工大学的Schmid 等［21］提出了一种高效的基于三维流场的特征值分析方法。由于全周计算域具有循环对称这一空间特性，基于全周计算域的特征值分析可以在考虑邻近通道的影响作用下仅根据基于单通道计算域进行的特征值分析结果计算得到。然而，文献［21］中使用了稀疏矩阵直接求解器进行大型稀疏阵的直接求逆［22］，计算的时间成本和内存消耗极高。如利物浦大学的Timme 所指出的，其极高的内存消耗可能成为研究计算量巨大的真实三维压气机流动失稳问题的瓶颈［12］。

为了克服试验测量和非定常数值模拟各自的缺点，受到北京航空航天大学孙晓峰团队，帝国理工Schmid 团队和利物浦大学Timme 团队等相关研究工作［12，17，21，23］的启发，本文提出了一种基于三维RANS 方程的能够精确解析真实压气机中三维几何和流动细节的高效特征值分析方法。由于这是对压气机流动进行完全基于三维RANS 方程的特征值分析的首次尝试，不失一般性，本文仅将该方法应用于某跨声速压气机环形叶栅算例中。实际上，该方法可以直接扩展到全三维压气机流动失稳问题的研究中。本文的总体结构如下：第1节对特征值分析方法的具体算法进行了介绍，包括定常流计算以及特征值分析算法2 部分。第2节对定常流动计算和特征值分析结果进行了讨论。最后，本研究的结论在第3 节中进行总结。

1 数值方法

1.1 流动求解器

本研究中所开展的定常、非定常模拟和特征值分析研究皆基于自研有限体积RANS 的CFD求解器NutsCFD。NutsCFD 能够在旋转坐标系下任意非结构化网格上实现定常、非定常流场求解。其算法和实现细节已在文献［24］中详细说明，此处不再详细论述，仅作简要介绍。

在以恒定角速度ω转动的固定在转子上的相对坐标系下，积分形式的流动控制方程为

式中：W为守恒变量；向量和分别为固定于转子参考系中的对流和黏性通量；Fω为由于旋转而产生的附加源项。它们的定义分别为

式中：ρ为密度；p为压力；T为温度；u为绝对速度；E为总能量；H为总焓；n为通量面单位法向量；τ为应力张量；κ为导热系数。除了平均流场的控制方程外，还包括由Spalart-Allmaras 湍流模型产生的一个额外方程［25-26］。

平均流场和湍流方程的对流通量均采用Roe格式进行离散。原始变量的梯度由格林高斯公式计算获得，用于从节点到通量面进行流动变量的外插值，从而使平均流场具有空间二阶精度。湍流方程的对流通量使用一阶迎风格式进行离散，以获得更好的收敛鲁棒性。时间离散基于全局化牛顿方法，采用伪瞬态延拓技术获得更为稳定的残差收敛性质。将所有空间离散通量和源项集中在一个向量R中，解向量W（包括平均流场和湍流变量，每个网格点6 个变量）基于全局化牛顿方法进行如式（3）所示的全隐式时间推进，直到找到稳态解。

在定常流场求解器的基础上，对时间离散项稍作修改即可得到利用二阶向后差分（Backward Difference Formula 2， BDF2）实现的双时间步时域非定常求解程序。对于一个给定的物理时间步长，内迭代仅需求解附加了时间源项的定常流场问题，同样可通过由ILU（0）预处理的GMRES 进行求解。

1.2 特征值求解器

空间离散后，半离散形式的流动方程可以表达为

式（4）可看作一个高维动力学系统。需要注意的是，为了与用于研究动力系统的符号使用习惯保持一致，右端残差项的符号与流动控制方程中的残差符号相反。此外，有限体积法产生的体积加权以及边界条件都已包含在残差函数R中。因此，右端项对于自变量W线化所产生的雅可比矩阵可准确描述非定常小扰动流场的时空变化信息。式（4）的特征值分解为

式中：J为由非线性残差精确线化得到的雅可比矩阵；v为对应于特征值λ的右特征向量。稳态流场计算完全收敛后，在最后一次非线性迭代期间计算的流场雅可比矩阵按相应节点的控制体积将每一行进行缩放并乘以负号后即可得到J。特征值分析是基于系统矩阵J进行的。

为计算矩阵J的特征值和特征向量，本研究中使用了隐式重启Arnoldi 方法（Implicitly Restarted Arnoldi Method， IRAM）［30］。所使用的广义特征值问题数学库为ARPACK［31］。为了更高效地使用内存并实现高效并行，ARPACK 与流场求解器通过子程序实现耦合，直接通过内存实现数据传递。与其他同样调用ARPACK 数学库的通用科学计算软件（如MATLAB［32］或SciPy［33］）相比，将ARPACK 程序包与流场求解器紧密耦合的优势在于更有效的内存使用和更容易的并行算法实现，这2 点优势对于大规模流动特征值计算都至关重要。IRAM 通过构建Krylov 子空间{b，Jb，J2b，…，Jm b}，并在子空间中找到最优近似解作为特征向量。如果需要内特征值（即离原点最近的特征值）和特征向量，则将Arnoldi 过程应用于系统矩阵的逆，即构建Krylov 子空间{b，J-1b，J-2b，…，J-m b}。此时，矩阵J的内特征值成为矩阵J-1的外特征值，而IRAM 应用于外特征值问题时更易收敛。由于高雷诺数流动问题空间离散产生的雅可比矩阵直接求逆的成本极高［22］，在IRAM 方法中，并不直接计算大型稀疏阵J的逆阵。事实上，每个Arnoldi 步骤本质上需要的仅仅是矩阵向量积J-1x，而非J-1。因此，可以使用非线性流场求解器中已有的大型稀疏线性系统求解器来执行每一步Arnoldi 过程，无需对矩阵J求逆。在这项工作中，流场求解器中的ILU（0）预处理的GMRES（程序需稍作改动以求解复值线性方程组）用于求解大规模稀疏线性方程组Jy=x以获得J-1x，用于在ARPACK 中构建IRAM 方法所需要的Krylov 子空间。当使用IRAM 方法进行特征值分析时，另一个需要提供的输入量是种子向量b。本研究中，种子向量b设为随机向量，原因是希望可以尽量保证所有特征向量在种子向量内都有相对平均的权重，从而不遗漏个别潜在的重要特征向量。此外，由于在特征值分析中并不计算所有特征值和特征向量，而是重点关注靠近虚轴的特征值，即接近失稳边界的模态。然而这些特征值不一定是最靠近原点的，因此有必要在原矩阵基础上施加一个复值的偏移量ζ，使得需要被求解的特征值在偏移后成为矩阵的内特征值从而被快速计算。实际操作中，首先根据工程经验预估关键特征值所在范围，选择某个相近的复数偏移量ζ并将其施加于原始系统矩阵J。矩阵J中最接近于ζ的特征值即转化为(J-ζI)的内特征值，其中I为单位矩阵。而矩阵(J-ζI)的内特征值可通过建立Krylov 子空间得到。同时，对矩阵施加一个复值偏移仅导致原始矩阵J的特征值偏移ζ，并不改变其特征向量。一旦获得了相关的特征值和特征向量，就可以在背景流场附近重构非定常流场。如果相关的特征值以共轭复数成对出现，即λ1，λ2，…，λn和，，…，，则重构的非定常小扰动场可表示为

式中：复系数ci和由扰动初始值W(t)|t=0确定。

2 计算结果

2.1 算例介绍

本文研究的压气机算例是通过将NASA Rotor 67［34］的三维计算域与一圆柱面相交而生成的环形压气机叶栅。所选用圆柱面半径为0.18 m，接近压气机50%叶高，此叶高处环形叶栅内流动为跨声速。三维转子和环形叶栅的几何及z-rθ坐标系下的展开视图如图1 所示。表1 列出了环形压气机叶栅的一些关键参数。此环形压气机叶栅算例流场中来流相对马赫数范围约为1.05～1.2，代表了现代航空发动机跨声速风扇叶尖附近截面的典型流场，因此本文中针对此算例开展研究。

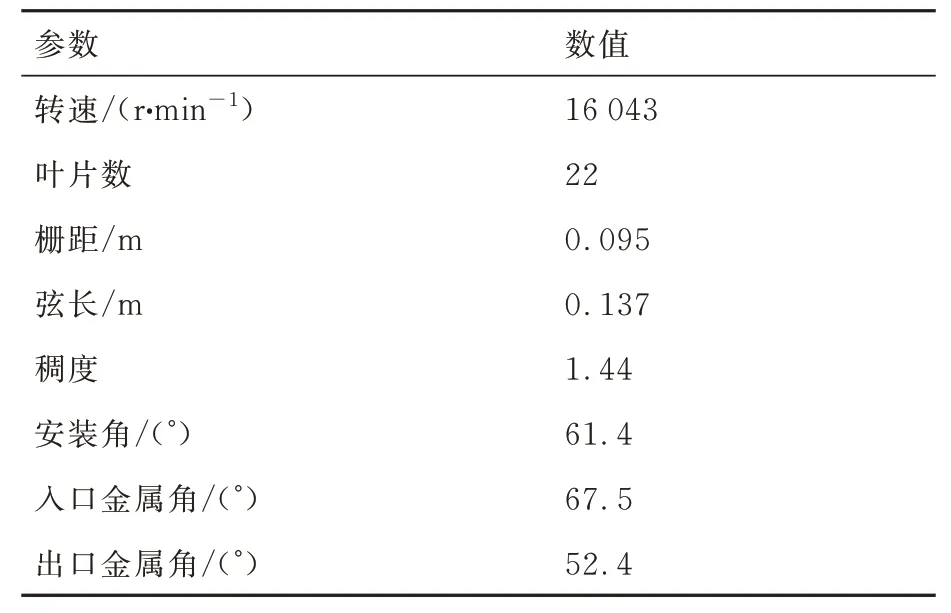
表1 环形压气机叶栅关键参数Table 1 Key parameters of annular compressor cascade

图1 NASA Rotor 67 与环形叶栅的几何示意图和流道内近峰值效率点压力云图Fig.1 Geometric diagram of NASA Rotor 67 and synthetic annular compressor cascade and pressure contours of flow path at near peak efficiency condition

2.2 稳态流场分析

为了计算稳态流场，使用NUMECA Autogrid 软件（版本13.2）生成了3 套逐渐加密的全周22 通道计算网格（如图2 所示），分别包含27 万、49 万和110 万个网格点，所有网格近壁单元厚度为3×10-6m，满足y+＜1。计算域进口边界位于叶片前缘上游1.5 倍弦长处，进口条件为总压101 325 Pa，总温288.15 K，且规定进气方向为轴向。计算域出口位于叶片尾缘下游2 倍弦长处，出口边界使用常数背压。所有计算中假定流动为完全湍流。为了获得压气机特性曲线，通过增加背压逐个计算稳态流场。当背压增量为50 Pa 就导致流场求解器不收敛时，即认为找到了失速边界。

图2 3 套计算网格Fig.2 3 sets of computational meshes

使用3 套网格计算的特性曲线如图3 所示。可见中网格与密网格特性计算误差不大且失速边界也很接近，因此可认为中网格已实现网格收敛。由于近失速点的流动特性是本文的主要关注点，因此详细检查了图3 中用实心红色符号标记的3 套网格上流量接近的工况（A， D， E）的流场细节。图4 比较了该流量工况不同网格上的压力云图，未观察到显著差异。图5 所示为沿叶片表面的压力分布对比，其中ptin为进口总压。可以看出，中、细网格的压力分布，包括前缘附近的压力尖峰，非常一致。而粗网格的结果与中、细网格结果有较大差异。这进一步表明，中网格足以捕捉足够的流动物理细节，可用于后续特征值分析，因此本文的分析皆基于粗网格和中网格开展。

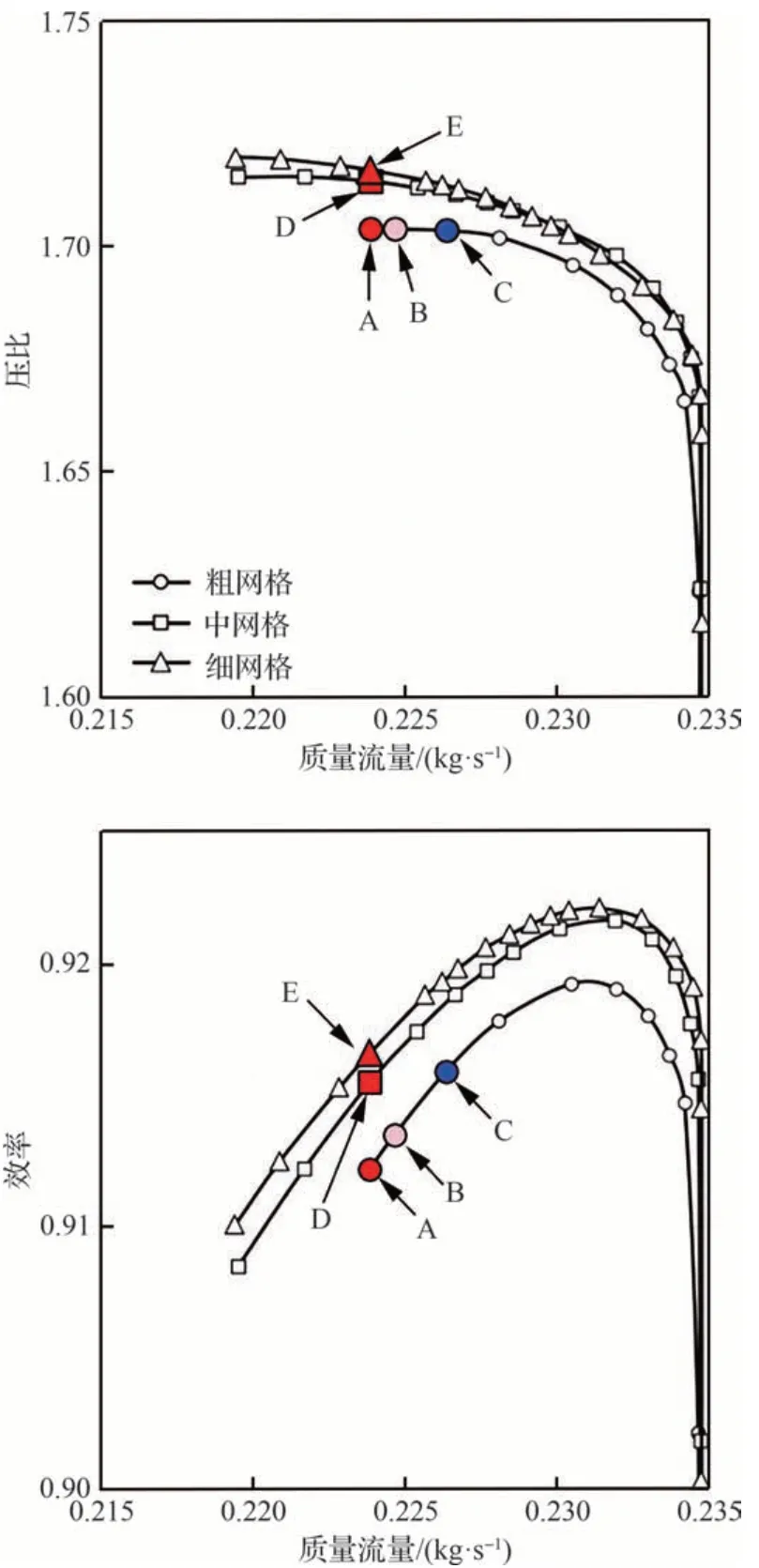
图3 3 套网格上计算的压气机特性线（带有实心红色标记的点A、D、E 具有几乎相同的质量流量，标有A、B、C 和D 的4 个数据点被用来进行特征值分析）Fig.3 Compressor characteristic curves computed on three meshes （Points A， D， E with solid red markers have nearly identical mass flow rates，and conditions labeled with A， B， C， and D are those for which eigenvalue analyses are performed）

图4 工况A、D、E 的压力云图Fig.4 Pressure contours for flow solutions under Conditions A， D， E

图5 不同网格下沿弦长的表面压力系数分布Fig.5 Surface pressure coefficient distributions along chord for different meshes

2.3 特征值分析

针对粗网格上3 个近失速工况（A、B、C）以及中网格上质量流量与粗网格失速边界接近的一个工况（D）进行特征值分析。为了寻找与旋转失速现象相关的特征值和特征向量，需依赖一定的工程经验，即模态波应具有与轴频率接近的特征频率。由于轴频率为

若将雅可比矩阵根据该角频率进行缩放，则所有与旋转失速模态相关的特征值都被缩放为模长量级为1 的复数。

首先对粗网格上近失速工况（性能曲线上标记为A）的流场进行特征值计算。由于没有关于特征谱的先验信息，因此首次特征值搜索具有一定的随意性，须通过试错来获得关键的特征值，即那些接近稳定边界（虚轴）的特征值。具体来说，将复值偏移量ζ设为(0.5n，0.5m)，其中整数n、m取值为n=-6，-5，…，2 和m=0，1，…，6。对每个偏移值计算10 个特征值/特征向量。全部特征值计算完成后，进行检查以确保找到复平面中矩形域( -3，1)×(0，3)内的所有特征值。所计算得到的特征值如图6 所示。可以看出，对于近失速工况A，存在6 个不稳定模态，这意味着通过强隐式求解器得到的全环稳态流场在物理上是不稳定的［35］。随后，按照与工况A 特征值分析相同的步骤，在流量较大的工况B 和工况C 进行特征值分析。工况B 和工况C 的特征值也画在图6中以进行比较。可以看出，随着工况从失速边界向更高的流量系数移动，特征值整体逐渐向左移动，意味着流动趋于稳定。表2 比较了3 个工况下最不稳定特征值的实部值。可使用分段线性插值来确定物理失速点流量为0.225 02 kg/s。根据相同的计算流程，还分析了中网格上工况D 的特征值，如图7 所示。可以看出，尽管A、D 这2 种工况流量几乎相同，但是中网格上工况D 不存在不稳定的特征值，比粗网格上工况A 更稳定。这与特性线计算时中网格上流场计算可以在更低的质量流量收敛到稳态解一致。

表2 工况A、B、C 下的最不稳定特征值Table 2 Least stable eigenvalues for Conditions A， B，and C

图6 工况A、B 和C 的特征谱（在所有特征值中，工况B的11 个特征值标记为λ1～λ11）Fig.6 Eigenvalue spectra under Conditions A， B， and C （among all eigenvalues shown， eleven for Condition B are labeled with λ1-λ11）

图7 工况A 与工况D 的特征谱Fig.7 Eigenvalue spectra under Conditions A and D

为了分析计算得到的特征值和特征模态，首先详细检查图6 中标记的11 个特征值及其对应模态。所选特征值分别记为λ1，λ2，…，λ11。编号的理由将在后续段落中解释。为了便于讨论，首先基于模态2～模态6（即5 个最不稳定的模态）重构时间相关的扰动场。具体来说，对于任一特征值λ及其特征向量v，可构造以下非定常流动扰动场为

式中：角频率ω为特征值λ的虚部。由于特征值实部仅决定模态振幅增长率，因此在重构中不予考虑。

基于式（8），可重构非定常流场扰动场͂(t)在一个周期的任意时刻的取值。在此工作中，仅在t=0，T4，T2，3T4 这4 个时刻重构流场，根据奈奎斯特采样定理，足以解析非定常扰动场的时空演化。其中T=2πω是对应模态的周期。需要注意的是，T对于每个模态都是不同的。

图8 展示了使用第2～第6 个模态重构的一个周期内的流场扰动场。首先可以看出，失稳模态在激波与激波后边界层及尾迹处幅值远高于流场中其他位置，体现出与激波边界层干涉极强的关联性。同时还可以发现，所有重构的非定常扰动场都是从压气机叶片的压力面传播到吸力面的行波，波数分别为2、3、4、5 和6，可以认为此即模态型失速试验中观测到的模态波。换言之，根据Schmid 等的理论推导［21］，它们是循环对称系统中某主模态在不同节径下的表示。尽管这里只显示了11 个被标记的模态中的5 个，但其余模态都遵循相同的规律，即具有不同节径，而它们的下标即每个模态各自的节径。表3 列出了在粗网格工况B 下不同模态波的节径和归一化转速。如图9 所示，与其他研究人员进行的典型计算和试验研究［36］中所发现的模态波转速与节径的关系相比，尽管压气机几何、运行条件和流动特性存在巨大差异，但仍能观察到模态波转速与模态节径数（即周向波数）的高度正相关性。这是首次使用数值方法系统地揭示了这种相关性，其与其他研究者所发现规律的高度一致性表明本文所提出的高保真特征值分析方法确实捕捉到了模态扰动的固有特性。需要强调的是，非定常模拟很难明确地获得多个失稳模态和接近失稳的稳定模态，特征值方法在揭示高维动力学系统的内蕴结构方面具有巨大的优势。

表3 工况B 下粗网格上计算的不同模态波的节径和基于转轴速度归一化后的转速Table 3 Nodal diameter and normalized rotating speed of modal waves which is normalized by shaft speed on coarse mesh under Condition B

图8 使用特征模态2～6 在一个周期内重构的轴向动量扰动场的时间演化Fig.8 Time evolution of axial momentum perturbation field reconstructed using Eigenmodes 2-6 over one period

图9 工况B 下绝对参考系中的归一化转速与模态波的节径之间的相关性及其与计算［7］和试验［36］结果的比较Fig.9 Correlation between normalized rotating speed in absolute frame of reference and nodal diameter of modal waves for Condition B compared to computational［7］ and experimental［36］ data

2.4 时域非定常模拟

为验证本文所提出的高效特征值分析方法的计算高效性和结果准确性，进一步针对粗网格近失速工况B进行了非定常模拟。非定常模拟由此工况完全收敛的定常流场进行初始化，通过双时间步方法进行时间推进，每一个物理时间步内的迭代采用Newton-Krylov 方法实现残差收敛。通过步长无关性研究后确定了物理时间步为0.36 μs，对应特征模态v3一个时间周期的1/200。非定常模拟总物理时间为3.3 s。在非定常模拟的基础上，监测图10 中叶片前缘附近绿色圆点所在位置静压值随时间的演化，压力扰动监测结果如图11 所示。首先可以发现，在最初的1.5 s 物理时间内，压力脉动值始终在10-10Pa 附近随机振荡。可以想象，若未先进行特征值稳定性分析，只通过非定常模拟进行研究，这一工况很可能被误判为稳定工况，这一现象体现了特征值方法进行稳定性分析的优势，即可以明确地判定流场的稳定性。从1.5 s 开始，监测点静压值开始指数增长。在约3.3 s 时，非定常流场中由于在计算域进口处出现回流，与所施加的总压、总温、轴向进气等进口边界条件冲突，导致计算迭代发散。由于本研究主要关注流场小扰动分析，而非充分发展的旋转失速现象，因此本工作中未再作调整计算域或边界条件以获得稳定的旋转失速现象的尝试。

图10 数值探针监控点位置示意图Fig.10 Position schematic diagram of numerical sensor

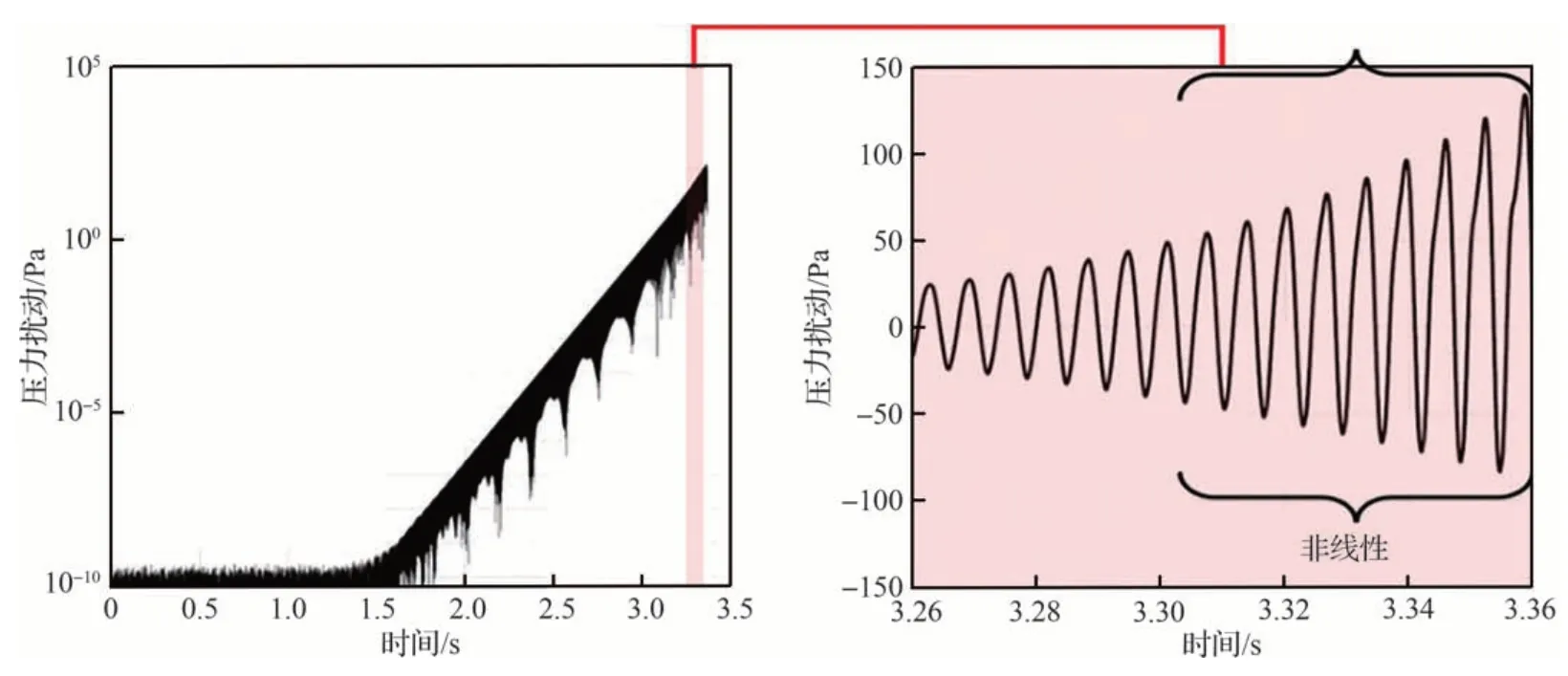
图11 数值探针位置处静压扰动变化曲线Fig.11 History of pressure perturbation at numerical probe position

为验证计算所得特征值和特征向量的准确性，将非定常流场投影到特征值分析获得的特征向量上进行非定常流场重构。为减小计算量，仅考虑图6 中的11 个特征模态及其共轭模态，即若令

则重构非定常流场可以表示为

为了获得η(t)，需要将式（10）两边分别左乘VH，即

系数向量η(t)的计算式为

式中：VHV为22×22 的方阵，只需对其求逆一次。对于VH͂(t)项，在每一物理时刻，将非定常扰动向模态矩阵V投影即可得到，计算量相比于流场计算也可忽略不计。在获得所有物理时刻的系数向量η(t)之后，即可通过获得基于最不稳定模态的重构流场。

图12 中显示了通过非定常模拟得到的流场(t)和重构流场中在监测点的静压扰动值各自随时间的演化历史。可见其在3.3 s 前吻合很好。3.3 s 后由于非定常流场本身出现非线性，重构信号逐渐偏离时域模拟信号。通过此比对可以确认特征分析的准确性。

图12 数值探针位置处非定常压力扰动与采用模态v3 与 重构得到的压力扰动的比较Fig.12 Comparison between unsteady pressure perturbation and reconstructed pressure perturbation by v3 and at numerical probe location

2.5 计算成本比较

本文工作中定常计算、特征值计算、非定常模拟都在24 核工作站上开展，所使用的中央处理器（Central Processing Unit， CPU）型号为Intel Xeon E52678W v4。为了定量分析计算效率，表4 列出了各类分析的实际计算时间。由于定常计算中各个工况的收敛速度依赖于初始化流场，且近堵点、最高效率点、近失速点的流场特性和收敛难度皆有所不同，因此对于定常分析单独列出了工况B 下定常流场计算和整个特性线计算各自的计算成本。对于特征值计算，由于对于一个新的算例，在初期需要一定的试错，以确保关键特征值都被找到，具体的试错成本与算例高度相关。因此特征值的计算成本仅考虑了计算最不稳定的10 个特征值和特征向量的计算成本。

表4 粗网格上3 类分析的计算成本Table 4 Computational cost of three types of analysis on coarse grid

从表4 中计算成本的分析可以看出，特征值分析与非定常模拟相比加速约155 倍，却获得了远比时域非定常模拟更为丰富的非定常小扰动流场信息。同时，特征值分析计算成本为单次定常流场计算的3.8 倍，且比特性线计算的成本要低很多，大约为计算整条特性线所需时间的28%。

3 结 论

1） 本文提出了一种适用于压气机三维流场流动稳定性研究的高效特征值分析方法，并用于分析代表了典型现代跨声速压气机叶片截面的环形压气机叶栅内流场的特征值和特征向量。将隐式重启Arnoldi 方法（IRAM）应用于内特征值分析，以识别与旋转失速现象关联最紧密的特征模态。内特征值分析使用了偏移求逆技巧。由于大型稀疏阵求解成本极大，因此利用大型稀疏线性方程组求解器，即ILU（0）预处理的GMRES 求解器的复值版本，等效地实现了求逆的效果。流场求解器中所采用的Newton-Krylov方法本就会计算雅可比矩阵，且此非线性流场求解方法已得到广泛验证，其计算效率可与最先进的CFD 求解器相媲美，经过简单修改就能够处理复值线性系统求解问题，从而进行大规模流动问题的特征值分析。与此同时，将较为成熟的特征值分析程序包ARPACK 与非线性流场求解器中的雅可比矩阵计算和线性求解器等现有程序相耦合，可实现工具库间的紧密数据传递，从而实现更高效的内存管理和更高的并行效率。本文所发展的高效特征值计算方法为基于三维流动控制方程的特征值分析在压气机流动稳定性问题上的首次尝试，由于其计算效率远高于时域非定常模拟计算方法（对于本文所研究算例，小扰动稳定性分析比非定常模拟加速约155 倍，仅为特性线计算的28%），使得基于小扰动分析的稳定性研究在考虑三维效应的压气机流动稳定性上成为可能。

2） 对于所研究的压气机算例，首先在失速点附近计算了若干深度收敛的稳态流场，然后使用上述特征值分析方法对部分近失速工况流场进行了特征值分析。由于特征值分析方法完全基于三维流动方程的精确雅可比矩阵，因此可获得极其丰富且与非定常小扰动流场分析完全一致的信息。同时，由于没有对压气机及其流动进行任何几何和流场简化，因此特征值和特征向量与非线性流动求解器所解析的流动物理完全一致。特征值分析结果表明，此压气机算例不稳定模态波对于流场的扰动主要体现在激波与激波后边界层，意味着旋转失速的发生与激波边界层干扰有关，为解释旋转失速失稳机理提供了一种重要思路。同时，所有特征值方法可以一次获得大量失稳或接近失稳的特征模态，发现在失速边界附近存在一系列具有连续变化的节径的特征模态。不同模态根据各自的节径和转速以行波形式朝叶片旋转相反方向传播。对于略超出失速边界的工况，数个特征模态会同时失稳，预示了失稳过程和失速后流场的高度复杂性。此外，本研究还探究了模态波转速与模态节径之间的关系，解释了试验中大量出现的模态波节径越大绝对坐标系下转速越高这一现象。通过本文研究可以看出，由于所发展稳定性分析方法的准确性和高效性，相比于非定常计算具有巨大的优势，为针对真实三维压气机模型的流动稳定性分析和失稳机理研究提供了重要的工具。