基于改进二阶优化器并行学习的弹道导弹神经网络落点预测方法

任乐亮，鲜勇，李少朋，2，雷刚，伍薇，李冰

1．火箭军工程大学 作战保障学院，西安 710025

2．清华大学 自动化系，北京 100084

为应对反导防御系统的拦截威胁，弹道导弹中段机动突防是目前最有效的方式之一。随着反导拦截系统的升级完善，传统采用射前突防/弹道/制导规划［1］，发射后只能沿给定弹道和给定策略进行机动突防的方法，面临战场动态适应能力不足的问题［2］。而基于弹载感知系统、智能决策算法和姿轨控动力系统的实时感知-自主决策-大机动的突防方式，将更加适应高动态的攻防对抗态势［3-4］。在该突防方式下，为保证落点精度，其制导方法设计面临严峻的挑战，主要原因：①弹道导弹大机动突防意味着大幅度偏离无机动标准弹道，基于无机动标准弹道设计制导算法将难以满足精度需求；②由于反导系统部署位置、拦截策略和拦截时机的不确定性，导致弹道导弹机动方向、机动时机和机动次数均具有一定的不确定性，从而无法在地面进行射前规划以解算机动突防标准弹道［5］。

而传统的弹道导弹制导方法主要是摄动制导［6］和闭路制导［7］，其中摄动制导依赖小偏差理论，无法满足大机动突防弹道导弹制导精度需求；闭路制导根据目标点及导弹飞行状态，按照控制泛函进行实时解算，并引入虚拟目标降低弹上计算复杂度，能够适应更大的弹道偏差。同时，闭路制导通常依据导弹当前状态和目标点状态实时更新虚拟目标点，进一步增强了算法的鲁棒性，而虚拟目标点的更新需要落点预测模型的支撑。针对大机动突防弹道导弹精确制导需求，文献［5］建立了一种基于模型预测控制思想［8］的落点预测制导方法［9-10］，由神经网络模型根据导弹当前运动状态预测落点，再与目标点进行对比，利用落点偏差解算制导控制量，进而完成落点修正。可以看出，闭路制导和文献［5］制导方法的关键都是如何解决弹道导弹落点的实时高精度预测问题。

目前，落点预测方法主要有弹道积分外推法［11］、基于椭圆弹道理论的预测方法［12］、基于近似解析表达式预测法［13-22］、神经网络非线性拟合法［23-26］。其中，第1 类方法预测精度高，但实时性差［27］，第2 类方法预测精度差，但实时性好，第3、4 类方法则在一定程度上兼顾了预测精度和实时性。基于近似解析表达式的预测法主要有状态空间摄动法［13-17］、经典fg 级数修正法［18］、中间轨道法［19］、非正交分解法［20-21］和平均轨道要素法［22］等，大量学者就此进行了研究，以解决闭路制导中在线计算虚拟目标的需求。其中，状态空间摄动法精度高于其他方法，同时，由于经典fg 级数修正法、中间轨道法、平均轨道要素法以时间为自变量，非正交分解法以射程角为自变量，因此当终端条件为地心距时，需要迭代计算，降低了计算效率，而状态空间摄动法则具有无需迭代计算的优点［15］。文献［13-17］基于状态空间摄动法对地球非球形摄动影响因素进行了解析建模，建立了无需迭代计算且具有较高精度的解析补偿模型，进而支撑了闭路制导在线补偿方法的研究。

但总体而言，基于近似解析表达式的预测法的解析建模门槛高、模型复杂，且相较于神经网络非线性拟合法而言，计算复杂度较高。神经网络非线性拟合法则具有简明的表达形式、规范的建模过程，同时由于其基于数据学习的特点，具有能够降低无解析模型因素对落点预测精度影响的特性。

近年来，学者们利用神经网络非线性拟合能力强和计算量小的特点，研究了其在落点预测中的应用，旨在平衡计算速度与预测精度，但现有神经网络落点预测方法仍有较大的改进空间。一是为提高落点预测精度，网络结构偏大，存在降低实时性的问题，如文献［26］设计的神经网络隐藏层节点数多达100 个，导致模型计算量较大。二是在网络输入输出量设计方面研究不足，导致学习难度大，如文献［5］通过改进激活函数、优化网络输入和解耦落点坐标等方法，在较小网络结构下实现了较高的预测精度，但由于仍采用神经网络输出落点坐标的设计模式，预测效率仍有提升空间。三是训练策略上有待深入研究，此类中小型网络通常在CPU 上采用LM（Levenberg-Marquardt）算法进行优化，具有收敛快、优化效果好的优点，但是随着样本数量及网络参数的增大，训练耗时将急剧增加。利用GPU 进行加速训练将极大地降低时间成本，但是在样本数量及网络参数较大的情况下，LM 算法对显存需求量很大。文献［28］所改进的LM 算法虽然有效降低了算法对存储量的需求，但是不利于GPU 并行计算。由此可知，研究多块GPU 训练环境下针对LM 算法的并行加速训练策略，是大样本神经网络落点预测模型的基础。

通常，虽然通过简化模型得到的预测结果存在一定的偏差，但是该偏差量相对于预测真值小很多，因此，以偏差量作为神经网络输出将有利于降低学习难度。比如，文献［26-30］分别针对落点预测问题、Lambert 制导和助推段弹道预测，以简化模型的预测偏差作为神经网络模型的学习量，得到了较好的预测结果。

基于上述分析，为降低神经网络学习难度，本文建立了一种神经网络学习椭圆弹道落点预测偏差的方法。本文主要贡献如下：①设计了一种弹道导弹落点预测框架，该框架由椭圆弹道落点预测模型和神经网络落点偏差预测模型组成，具有预测精度高、网络结构小和实时性好的特点；②基于Levenberg-Marquardt 算法设计了一种并行学习优化器，降低了算法对显存的需求量且缩短了学习耗时；③对同一型号导弹而言，无需射前对神经网络进行训练，有利于缩短诸元准备时间。

1 弹道导弹落点预测问题

1.1 基本假设

本文建立的落点预测模型旨在为中段大机动突防弹道导弹制导方法研究提供参考，在制导方法误差评价范围内表示落点预测误差。因此，不考虑弹道导弹实际再入过程中的气动系数、大气参数和风场与地面解算弹道使用的气动系数、大气参数和风场之间偏差等非制导因素对落点影响［31］。基本假设如下：

1） 地球模型采用考虑J2项摄动影响的旋转椭球体模型。

2） 弹道导弹再入大气层后，保持零攻角和低速慢旋稳定状态进行无动力飞行，忽略马格努斯力的影响。

3） 考虑到不同季节的大气参数和风场有所差异［31-32］，因此，针对不同季节生成相应的训练样本并进行训练。射击前，根据季节选择相应的神经网络落点预测模型装订上弹。后续将以特定的大气模型作为落点预测仿真分析的基础，不影响制导方法误差评价范围内落点预测模型的精度和计算复杂度研究。

1.2 落点预测形式化描述

根据弹道导弹弹道学可知，在标准弹道条件下，以任一飞行状态为起始点，对应唯一一条弹道，这也是落点可预测的基础。因此，可以建立落点预测的形式化描述如式（1）所示，其关键是如何得到式（1）中的映射f。

式中：S0∈Rn×1表示导弹运动状态矢量，n为运动状态变量的个数；P∈R3×1表示落点矢量。为方便描述，如不特指文中均采用列矢量形式。

1.3 精确落点解算模型

在地心地固（Earth-Centered Earth-Fixed，ECEF）坐标系下，建立考虑旋转椭球体和再入阻力模型的动力学方程：

式中：t为飞行时间；Xs和Vs分别为t时刻弹道导弹在ECEF 坐标系下的位置和速度矢量和分别为t时刻弹道导弹在ECEF 坐标系下引力、空气动力、牵连惯性力和柯氏惯性力的加速度矢量，可由式（3）计算得到：

式中：μ为地球引力常数为导弹地心距；J2为地球形状动力学系数；ae为地球长半轴；φs为地心纬度；ωe=[0，0，ωe]T为ECEF 坐标系下的地球自转角速度矢量，其中，ωe为地球自转角速度大小；mw为质量；ρ为大气密度；CD为阻力系数；Sw为最大横截面积；Vs，wind=Vs-Vwind为ECEF 坐标系下导弹相对于空气的速度［33］，Vwind为ECEF 坐标系下的风速；“×”表示叉乘。

采用阿达姆斯数值积分方法［34］对式（2）进行求解，即可得到落点，积分结束条件为

式中：rm为目标点的地心距；rs为导弹地心距。

2 神经网络学习椭圆弹道落点预测偏差模型

2.1 椭圆弹道模型

为方便描述，定义落点预测时刻的ECEF 坐标系为地心惯性（Earth-Centered Inertial，ECI）坐标系，即落点预测瞬间ECEF 坐标系与ECI 坐标系一致，但由于ECEF 坐标系随地球自转而旋转，其他时间不再重合。ECI 坐标系与ECEF 坐标系运动状态矢量之间的转换关系为

式中：XECI和XECEF分别为ECI 坐标系和ECEF 坐标系下的位置矢量；VECI和VECEF分别为ECI 坐标系和ECEF 坐标系下的速度矢量(Δt)为ECI 坐标系与ECEF 坐标系的转换矩阵，其表达式如式（6）所示；Δt为ECEF 坐标系相对ECI 坐标系旋转的时间，可知，落点预测时刻Δt=0，导弹落地时刻Δt=tf，tf为导弹自当前状态飞行至落地所经历的时间。

由于椭圆弹道理论忽略了地球非球形摄动以及再入大气阻力影响，在ECI 坐标系下为平面弹道，利用该特点可建立落点预测解析模型。为方便求解落点，以轨道根数E描述椭圆弹道：

式中：h、i、Ω、e、ω和θ分别为比角动量的模、轨道倾角、升交点赤经、偏心率、近地点幅角和真近点角，如图1 所示，其中：h为比角动量矢量；e为偏心率矢量；Oe为地心。

图1 轨道根数示意图Fig.1 Schematic diagram of orbital elements

2.1.1 解算落地时刻的轨道根数

式中：h0、i0、Ω0、e0、ω0和θ0分别为落点预测时刻的比角动量的模、轨道倾角、升交点赤经、偏心率、近地点幅角和真近点角。

在椭圆弹道假设下，导弹与地球为二体系统，可得导弹落地时刻的轨道根数Ef为

式中：θf为落地时刻的真近点角，考虑到导弹落地时的径向速度小于0，可得θf为

2.1.2 解算ECEF 坐标系的落点矢量

根据落地时刻的地心距和真近点角，可得近焦点坐标系［35］下落点为

根据近焦点坐标系与ECI 坐标系转换关系可得ECI 坐标系下落点为

式中：为近焦点坐标系到ECI 坐标系的转换矩阵［35］。

由于地球旋转因素影响，为得到ECEF 坐标系下的位置，需要进一步求解飞行时间tf。考虑到平近点角反映了轨道的平均角运动，可得tf为

式中：T为轨道周期；M0和Mf分别为落点预测时刻和落地时刻的平近点角。

将式（11）～式（13）代入式（5）后可得ECEF坐标系下的椭圆弹道预测落点矢量为

为方便描述，将基于椭圆弹道的落点预测模型表示为fET，可得

2.2 神经网络落点偏差预测模型

2.2.1 坐标系定义

为降低神经网络学习难度，在坐标系建立神经网络落点偏差预测模型。与文献［5］中定义的坐标系类似，不同的是文献［5］坐标原点定义在弹下点m0处，而本文坐标原点定义在当前飞行位置m1处，具体定义为：以m1为坐标原点，轴过地心Oe与m1连线，且指向天为正轴指向VECEF与轴的叉乘方向，轴与轴、轴构成右手直角坐标系，如图2 所示。

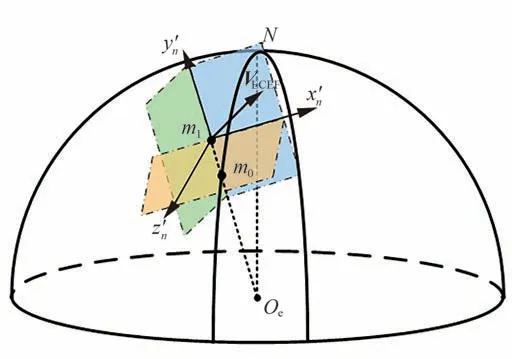
图2 坐标系示意图Fig.2 Schematic diagram of coordinate system

坐标系与ECEF 坐标系的转换关系为

式中：为导弹在坐标系的位置矢量；为ECEF 坐标系到北东坐标系的旋转矩阵［36］，如式（17）所示；为北东坐标系到坐标系的转换矩阵，如式（18）所示；H0为落点预测时刻导弹的高度。

式中：φs，0和λs，0分别为落点预测时刻的地心纬度和地心经度。

式中：γ为轴与正北的夹角，当轴在北向偏东时为正。令导弹在北东坐标系下的速度可得：

2.2.2 神经网络模型设计

1）神经网络输入输出量设计

考虑到落点在坐标系的不同分量具有较大的差异性，为降低学习难度，构建3 个神经网络（多层感知机形式）分别学习椭圆弹道落点预测误差在坐标系的3 个分量，因此，构建神经网络落点偏差预测模型为

神经网络输入量的选取，将直接影响模型学习的难易。考虑到不同纬度φs，0、不同飞行高度H0、不同高度差ΔH=H0-Hm（Hm为目标点高度）对落点有影响，同时加入当地弹道倾角Θ0、速度方位角σ0和ECEF 坐标系下的速度大小作为网络输入有助于模型学习［5］，令网络x、y和z的输入和分别为

2）神经网络结构设计

fxNN(·)、fyNN(·) 和fzNN(·) 采用多层感知机形式，所不同的是网络模型的输入输出量、隐藏层层数以及节点数目。图3 给出了含有2 个隐藏层的神经网络示意图。

图3 网络结构示意图Fig.3 Schematic diagram of network structure

在确定fxNN(·)、fyNN(·)和fzNN(·)的隐藏层层数和节点数时，为了使神经网络获得良好的泛化能力进而获得更好的预测效果，可以在一定程度上增加网络的隐藏层层数和节点数量。但过多的隐藏层会导致学习时间过长和学习过程不稳定，并会导致网络出现“退化”现象［37］，因此设定最多采用2 个隐藏层的网络结构。

为降低神经网络模型的计算复杂度，在确定网络结构时，应在满足精度要求的前提下尽可能减小网络结构，即选择合适的隐藏层层数及节点数。根据Kosmogorov 定理可知，含有1 个隐藏层的神经网络可以完成任意的n维到m维的映射［38］。因此，在确定网络结构时首选隐藏层数为1，但是随着隐藏层节点数的增加，网络计算复杂度将逐渐变大。考虑到增加隐藏层层数会提高神经网络预测精度，因此，合理设计双隐藏层的节点数，在相同预测精度下，具有比一个隐藏层更小计算复杂度的可能性。

同时，考虑到隐藏层层数和节点数不仅与输入输出层的节点数有关，更与需解决问题的复杂程度、激活函数以及样本数据的特性等因素有关［39］。因此，为建立适用于高精度快速落点预测的神经网络模型，采用网络结构增长型方法进行仿真计算［38］，确定隐藏层层数以及节点数量，详细仿真实验见3.1 节。

3）激活函数选取

激活函数的选择对神经网络而言十分重要，通常在浅层网络中采用Sigmoid 和Tansig 函数作为激活函数，具有较强的非线性拟合能力。但是，由于此类激活函数中包含指数运算，计算量较大，不利于提高模型实时性。因此，采用文献［5］建立的S-Sigmoid 激活函数。该函数具有与Sigmoid函数相近的拟合水平，但是计算量小于Sigmoid函数。S-Sigmoid 激活函数为

式中：x为S-Sigmoid 函数输入量。

2.2.3 神经网络样本生成

为提高神经网络预测精度，学习样本需覆盖落点预测时刻所有可能的飞行状态范围。定义落点预测时刻的飞行状态集合S为

式中：H0、Hm、φ0、、σ0和Θ0分别为离散化后的初始飞行高度、目标点高度、纬度、速度大小、速度方位角和当地弹道倾角集合，离散间隔分别为δH，0、δH，m、δφ、δV、δσ和δΘ。

考虑样本范围越大，则需要越大的神经网络结构来完成较高精度的拟合，为降低神经网络结构大小，提高计算效率，按照高度对落点预测时刻的飞行状态空间集合S进行分解。 令Si⊂S(i=1，2，…)，则可得

式中：H0，i⊂H0，同时

针对集合Si生成训练集并进行训练，从而得到对应的神经网络模型；在弹上落点预测阶段，根据飞行高度选择对应的神经网络模型即可完成落点预测。

集合Si的训练集样本的生成过程为，即神经网络的样本输入，根据文献［5］的方法将其转换到ECEF 坐标系，得到式（2）所给微分方程组的初值，再根据1.1节给出的精确落点解算模型得到落点在ECEF 坐标系的落点。结合式（16）可得神经网络样本输出ΔpET的标签为

集合Si的测试集样本生成方法为：以H0，i、Hm、φ0、、σ0和Θ0确定的上下界为范围，令各变量服从均匀分布，随机生成初始状态，并采用与生成训练集样本相同的方法，得到样本输出ΔpET。

2.2.4 神经网络训练

1）归一化处理及损失函数选取

为克服输入向量的不同维尺度不统一带来的训练效率低的问题，采用min-max 归一化方法对数据进行归一化处理：

式中：p表示变量；pmin表示变量的最小值；pmax表示变量的最大值；p͂为归一化后的结果。

模型学习采用MSE 损失函数：

式中：M为样本数量；N为神经网络输出值的数量；yi，j和分别为第i个样本的第j个输出量的预测值和标签值。

2）优化器设计

LM 算法是中等规模神经网络学习算法中最快的一种［40-41］，属于牛顿法的改进，是一类二阶优化器，相较于AdaGrad［42］、RMSPRop［43］和Adam［44］等一阶优化器而言具有整体收敛速度快、优化精度高等特点。其迭代公式为

式中：mn=M·N为所有样本标签值的数量；下标l表示迭代代数；x∈Rk×1为网络参数组成的向量，即各网络层的权值和阈值，其中，k为网络参数的数量；J∈Rmn×k为输出量对网络参数的雅克比矩阵；E∈Rmn×1为神经网络预测值相对于标签值的误差向量；I∈Rk×k为单位矩阵；μ'为动态更新的参数，若更新网络参数减小了网络预测误差，则令μ'←μ' kμ'，否则令μ'←μ'·kμ'，再次计算网络参数更新量，其中，kμ'为大于1 的超参数。

J和E的大小会随着M的增大而增大，当采用GPU 加速学习时，求解J和E以及执行JTJ和JTE运算会占用大量显存，将无法在小显存GPU上运行。本文在文献［28］基础上，进一步借鉴矩阵分块思想对LM 算法进行改进，以降低显存需求量，同时，针对改进的LM 优化器设计了一种多GPU 并行加速机制，有效提高了学习效率，称之为改进的数据并行LM 优化器（Improved Data Parallel Levenberg-Marquardt，IDP-LM）。

① 改进Levenberg-Marquardt 优化器

对J和E分块：

式 中 ：Ji(i=1，2，…，NGPU) 和Ei(i=1，2，…，NGPU)分别为J和E的子矩阵；NGPU为参与学习的GPU 的数量。

根据分块矩阵运算法则可得

由式（30）可知，第i块GPU 仅需要求解Ji、Ei、JTi Ji和JTi Ei，由此可实现JTJ和JTE的并行求解，提高学习效率。

为降低每块GPU 对显存的需求量，进一步将Ji和Ei均匀分块为

式中：Ji，j(j=1，2，…，ϑi) 和Ei，j(j=1，2，…，ϑi)分别为Ji和Ei的子矩阵；ϑi=[mi ζi]+1 为子矩阵的个数，其中，mi为Ji和Ei行数，ζi为Ji，j和Ei，j(j＜ϑi)的行数，[·]表示取整。

将式（31）代入式（30）得：

由于第i块GPU 一次仅需要求解Ji，j、Ei，j、，j和，j(j≤ϑi)，在一定程度上能够减轻算法对每块GPU 显存的需求量。

将式（32）代入式（28）可得IDP-LM 算法的网络参数更新公式为

② 并行学习流程

为更好地说明IDP-LM 并行学习流程，以2 块GPU 并行学习为例，如图4 所示，给出其并行学习流程如下：

图4 IDP-LM 并行学习框架Fig.4 Parallel learning framework of IDP-LM

步骤1将学习数据均匀分发到GPU 1 和GPU 2。

步骤2将GPU 1 中网络模型的参数分发到GPU 2，并据此更新GPU 2 中模型的参数。

步骤3GPU 1 和GPU 2 分别将各自的数据代入网络模型，得到各自的雅克比矩阵和误差向量，并分别计算1与1J2与2。

步骤4将GPU 2 中的2与2发送到GPU 1，并在GPU 1 计算式（30）。

步骤5在GPU 1 中根据式（33）计算网络参数更新量并更新GPU 1 中的网络参数，然后转到步骤2。

2.2.5 总体框架

结合式（15）、式（16）和式（20）可得落点预测模型为

建立落点预测总体框架如图5 所示，预测算法流程如算法1 所示。

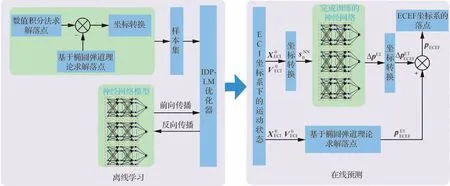
图5 落点预测总体框架Fig.5 Overall framework of impact point prediction

3 仿真分析

为对建立的落点预测算法进行验证，在加入机动突防条件下，以H0，1=[100，200] km 为例，通过大量弹道仿真，确定落点预测时刻的飞行状态集合S1的范围如表1 所示。

表1 仿真参数范围Table 1 Range of simulation parameters

在表1 所给飞行状态范围和离散间隔的基础上，利用第2节训练集样本生成方法得到859 320个样本作为训练集。为更好地测试神经网络预测模型的泛化能力，再结合第2 节测试集样本生成方法，以表1 给出的各变量的上下界为范围，得到生成12 000 个随机样本，将其中10 000 个样本作为测试集，另外2 000 个样本作为验证集。仿真平台性能如下：操作系统为Ubuntu 18.04，CPU为Intel酷睿10980XE，内存为32 GB，深度学习框架为Pytorch 1.10，显卡为英伟达3090（24 GB）。

3.1 神经网络预测模型网络结构

在2.2.2 节基础上，进一步确定神经网络预测模型的隐藏层层数和节点数。为提高网络计算速度，确定神经网络各隐藏层的节点数时，在落点预测精度的约束下，应尽可能减小隐藏层节点数。在网络模型、和均含有1 个隐藏层情况下，仿真分析了不同节点数对预测精度的影响。为方便描述，定义E3σ为训练集预测误差集合和测试集预测误差集合并集的3σ值。针对每种情况各训练10 次，最大训练代数为10 000，统计10 次E3σ得到箱线图如图6～图8所示。

?

图6 含1 个隐藏层条件下的E3σ 箱线图Fig.6 Boxplot of E3σ for with one hidden layer

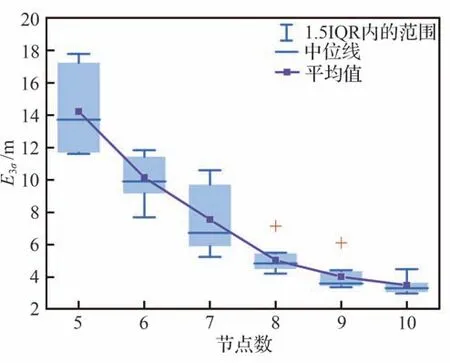
图7 含1 个隐藏层条件下的E3σ 箱线图Fig.7 Boxplot of E3σ for with one hidden layer

图8 含1 个隐藏层条件下的E3σ 箱线图Fig.8 Boxplot of E3σ for with one hidden layer

由图6～图8 可得，随着节点数的增加，3 个网络模型的预测精度均逐渐提高。当模型和的隐藏层节点数分别达到8 和5 时，E3σ的中位数小于5.0 m；当模型的节点数为18时，E3σ的中位数在10.0 左右。而随着节点数的增加，预测精度提高缓慢，若采用增加节点数的方法来提高预测精度，不利于网络结构的减小。因此，为进一步探索更小的网络结构，将网络模型设计为2 个隐藏层，并令、和的隐藏层1 的节点数分别为11、6 和5，仿真得到隐藏层2 节点数取不同值时对预测精度的影响，如图9～图11 所示。

图9 含2 个隐藏层条件下的E3σ 箱线图Fig.9 Boxplot of E3σ for with two hidden layers

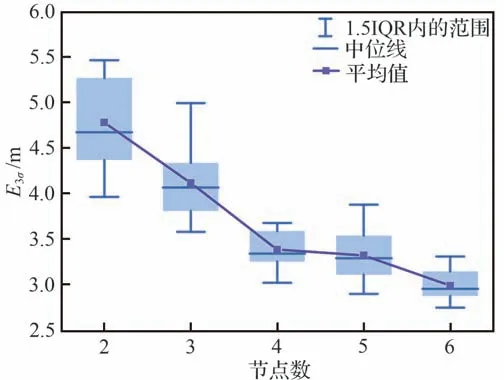
图10 含2 个隐藏层条件下的E3σ 箱线图Fig.10 Boxplot of E3σ for with two hidden layers

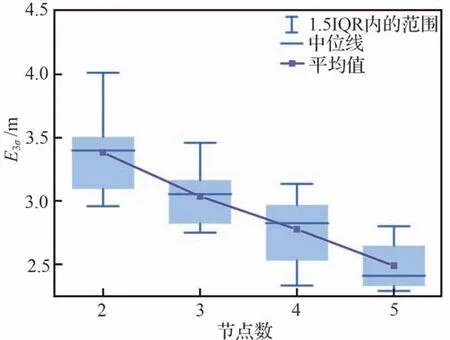
图11 含2 个隐藏层条件下的E3σ 箱线图Fig.11 Boxplot of E3σ for with two hidden layers

表2 本文模型网络结构Table 2 Network architecture of the proposed method

3.2 落点预测精度

为验证所提方法在预测精度上的优势，对训练集和测试集中共869 320 个样本进行测试，其中，10 000 个测试样本的存在，可以验证模型的泛化能力。图12 给出了预测模型对ΔpET3 个分量预测误差的绝对值以及落点预测误差大小‖ΔpET‖的箱线图。由图12 可知，预测模型的精度较高，预测误差的3σ值和平均值分别为4.97 m和1.16 m，说明本文预测方法具有较强的泛化能力，能够满足制导方法对落点预测精度的需求。

图12 落点预测误差箱线图Fig.12 Boxplot of impact point prediction deviations

为进一步分析神经网络落点预测模型精度的影响因素，利用控制变量法对落点预测时刻的飞行高度、目标点高度、纬度、速度大小、速度方位角和当地弹道倾角对预测精度的影响进行了仿真分析，即分别固定上述变量不变而其他变量按照表1 所给范围进行离散采样，得到不同影响因素对落点预测误差大小的箱线图如图13 所示。

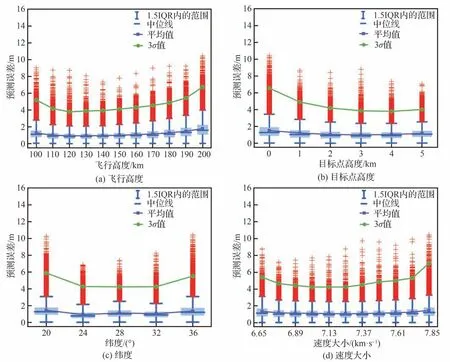
图13 不同因素对落点预测精度的影响Fig.13 Influence of different factors on impact point prediction accuracy

由图13 可知，总体来看，处于飞行状态范围边界的预测精度低于预测范围中间的预测精度；同时，由图13 （a）、图13（c）和图13（d）可知，随着飞行高度、纬度和速度大小的增大，预测误差呈现增大趋势，其中，飞行高度和速度大小因素对应的趋势更明显。由图13 （b）可知，随着目标点高度的增大，预测精度呈现变好的趋势；由图13 （f）可知，随着当地弹道倾角逐渐增大，落点预测误差的平均值和3σ值曲线上升明显，说明当地弹道倾角对预测精度影响较大。同时，在当地弹道倾角小于-15.5°时，其3σ预测误差小于3.5 m，而其他因素对应预测误差的3σ值均高于3.5 m，说明当地弹道倾角对预测精度的影响高于其他因素。

分析上述原因可知，当地弹道倾角增大、高度变大、速度变大、纬度变高以及目标点高度变小将引起飞行时间增长，增大了由于再入阻力和非球形摄动引起的落点非线性化程度，进而增加了预测难度。

由图13 （e）的平均值曲线可知，当速度方位角在90°和270°附近时，曲线处于波峰状态，说明预测模型对于向东或向西飞行的导弹的落点预测误差相对较大，同时，预测误差的3σ曲线的波峰和波谷相近，说明由于速度方位角不同而引起的预测误差差别不大。

为进一步验证本文方法在网络结构上的优势，与文献［5］进行了对比仿真分析，其中，为适应本文落点预测问题的背景，在文献［5］所给3 个神经网络模型的基础上，增加ΔH作为输入量，同时，以落点在m1x'n yn z'n坐标系的3 个分量作为输出，将上述3 个网络分别记为(·)(·)和(·)。令文献［5］模型的各隐藏层节点数如表3 所示，本文方法各隐藏层节点数如表2 所示。针对每种方法各训练10 次，本文方法最大训练代数为10 000，文献［5］最大训练代数为20 000，统计10 次E3σ得到箱线图如图14 所示。考虑到神经网络模型的复杂度基本由乘法量和激活函数个数来决定，因此，为初步计算网络模型复杂度，统计各方法的激活函数个数和乘法量如表4所示。

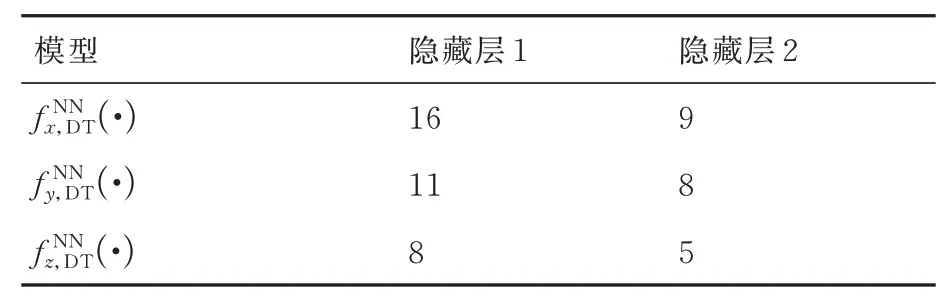
表3 文献［5］网络结构Table 3 Network architecture of Ref.［5］

表4 本文方法和文献［5］模型的复杂度Table 4 Computational complexity of the proposed method and Ref.［ 5］

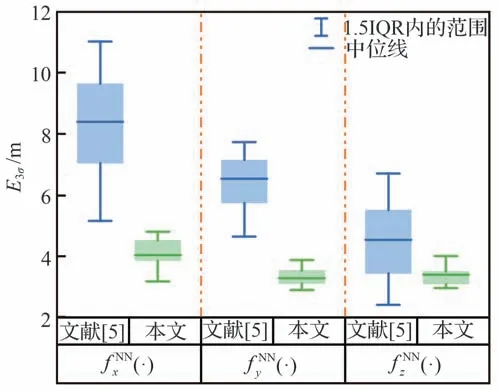
图14 本文方法和文献［5］模型的E3σ 箱线图Fig.14 Boxplot of E3σ for the method in this paper and in Ref.［5］

由图14 可以看出，在上述网络结构下，本文方法的预测精度优于文献［5］方法；同时，由表4 可知，本文方法的网络结构远小于文献［5］的网络结构，激活函数个数少于后者，且乘法量仅为后者的51.5%。说明以椭圆弹道预测误差作为标签，有利于降低网络学习难度，从而可以降低网络结构大小，降低模型计算复杂度。

考虑到初始飞行状态范围变大时，会增加学习的难度，进一步仿真分析了本文方法和文献［5］方法在针对该问题上的敏感性，即测试初始飞行状态范围变大时，同一网络结构对应预测模型的精度是否受到较大影响。分别在H0，1、Hm、φ0和Θ0原有范围（如表1所示）的基础上，增加1 倍对应离散间隔，针对每种情况训练10次并记录相应的E3σ，统计2种方法的E3σ箱线图如图15所示。

图15 增大初始状态范围后本文方法和文献［5］模型的E3σ 箱线图Fig.15 Boxplot of E3σ for the proposed method and Ref.［5］ after expanding range of initial states

可以看出，初始飞行状态范围的变大对2 种模型关于落点z方向的预测精度影响最小，而关于x、y方向的预测精度影响较大。分析原因可知，由于导弹近似在坐标系的平面飞行，使得落点z轴分量与x、y轴分量解耦，故落点的x、y轴分量受飞行状态范围影响较大，从而增加了网络模型学习落点的x、y轴分量的难度。同时，改变不同变量范围对2 种神经网络模型预测精度影响不同，总体而言，本文方法受初始飞行状态范围变大的影响更小，具有“小网络预测大范围”的潜力。

3.3 消融实验验证所提模块的有效性

为测试本文方法的各模块对整体预测精度提高的有效性，设计消融试验研究了各模块对预测精度的影响。

3.3.1 在m1x'n yn z'n坐标系表示落点对预测精度的影响

图16 以不同坐标系下落点作为标签的E3σ 箱线图Fig.16 Boxplot of E3σ for network architecture with the impact point as label in different coordinate systems

总体来看，以ΔpET作为样本标签对应的网络预测精度高于另外两者，以作为样本标签对应的网络预测精度最低，说明在坐标系表示样本标签有利于神经网络学习。

3.3.2 建立3个网络分别预测落点3个分量有效性

为检验建立3 个网络分别预测落点3 个分量的有效性，需要验证该方法是否在降低网络结构大小的同时保持了预测精度。建立映射fNN1如式（35）所示，该网络模型含有2 个隐藏层，输出节点数为3。

针对fNN1隐藏层1 和2 分别为15 和10、17 和16 以及20 和15 这3 种情况，分别称之为工况1、工况2 和工况3，对模型fNN1训练10 次，最大训练代数为10 000，统计神经网络输出二范数‖‖ΔpET的E3σ得到箱线图如图17 所示。同时，图17 给出了采用本文方法得到‖‖ΔpET的E3σ箱线图。可以看出，本文方法与隐藏层1 和2 分别为17 和16 的fNN1模型精度相当，优于隐藏层1 和2 分别为15和10 的fNN1模型，略差于隐藏层1 和2 分别为20和15 的fNN1模型。在网络结构大小方面，隐藏层1 和2 分别为17 和16 的fNN1的乘法量达到了473，是本文方法的1.58 倍；隐藏层1 和2 分别为20 和15 的fNN1的乘法量达到了525，是本文方法的1.75 倍，可知本文方法的网络结构远小于此两者。说明利用3 个网络分别预测落点3 个分量有利于提高预测精度，降低网络结构大小。

图17 不同网络模型的E3σ 箱线图Fig.17 Boxplot of E3σ for different network models

3.3.3 IDP-LM 算法有效性

LM 优化器收敛速度快、训练效果好，但显存需求量大，因此，在样本数量大且网络结构大的学习场景下，往往面临显存不足的问题；同时，在单个GPU 上的训练耗时较长。为验证本文建立的IDP-LM 优化器对显存需求和并行计算上的优势，以本文中出现的5 个不同网络模型为验证对象，统计各模型训练的显存占用量和训练耗时如表5 所示。

表5 训练耗时和显存占用量Table 5 Training runtime and GPU memory consumption

表5 给出了不同模型在单个GPU 上训练以及采用IDP-LM 优化器在2 个GPU 上各训练10 次的平均耗时，其中，每次均训练1 000 代。可以看出，当网络结构较大时，采用IDP-LM 优化器能够显著降低训练耗时，如fNN1模型隐藏层1和2 分别为20 和15 时，训练耗时降低率高达49.18%，即相比于传统LM 优化器而言可以降低一半的训练耗时；而对于网络结构较小的模型而言，采用IDP-LM 优化器能够降低耗时，但效果不太明显，如模型隐藏层1 和2 分别为5和2 时，耗时降低率仅为32.3%。其主要原因是，IDP-LM 优化器在多个GPU 间存在一定的通信损耗，同时，由步骤4 和步骤5 可知，需要在GPU1 上进行串行计算。由于该部分耗时很小，因此，在网络结构较大时，占总耗时比例很小；而在网络结构较小时，其耗时所占比重有所增加。由此可知，针对网络结构较大的落点预测模型训练而言，能够有效降低训练耗时。

表5 给出了不同模型在单个GPU 上训练以及采用IDP-LM 优化器在2 个GPU 上训练的显存占用情况。可以看出，在GPU 数量一定的情况下，ϑ1=ϑ2=1 对应的显存占用量大于ϑ1=ϑ2=2；在ϑ1和ϑ2一定的情况下，单个GPU 训练对应的显存占用量大于2 个GPU 训练对应的显存占用量。同时，由于Pytorch 深度学习框架自身占用一定的显存，因此，对于网络结构较小的模型训练而言，采用IDP-LM 优化器后显存占用降低不太明显；而对于网络结构较大的模型训练而言，IDP-LM 优化器在降低显存占用方面作用明显。

3.4 算法复杂度

3.2 节初步给出了网络结构大小的初步衡量方法，但是难以衡量激活函数个数不同且乘法量不同模型的网络结构大小。因此，为更精确地衡量网络结构大小，同时检验落点预测算法的实时性，以STM32F407 单片机为实验平台，对本文算法和文献［5］算法的CPU 耗时进行了测试，其中，单片机运算数据类型为double，网络结构分别如表2 和表3 所示。表6 给出了单次预测总耗时、神经网络模型耗时、椭圆弹道预测耗时以及其他耗时（神经网络模型输入输出数据处理耗时等）。

表6 不同模型计算耗时Table 6 Runtime of different models

由表6 可得，本文方法的预测总耗时比文献［5］方法的预测总耗时少0.41 ms。其中，椭圆弹道预测耗时为0.634 ms，占总耗时的24.53%，该部分耗时不受网络结构大小的影响；神经网络模型耗时为1.250 ms，占总耗时的48.36%。由3.2 节可知，表2 和表3 给出的网络结构对应的落点预测精度相当，但本文方法的神经网络耗时相比于文献［5］的神经网络耗时少1.049 ms，降低了45.6%。由此可得，本文预测模型能够降低预测耗时，提高模型的实时性；同时，由于神经网络预测模型的计算复杂度随着初始飞行状态范围的变大而增加，而椭圆弹道预测模型的计算复杂度基本稳定，因此，在大范围飞行状态的预测问题中，本文方法具有更大的优势。

4 结 论

针对弹道导弹大机动突防后的制导方法设计面临的落点预测需求，建立了一种神经网络学习椭圆弹道落点预测偏差模型，在一定程度上为该问题的解决提供了较好的参考，具体内容总结如下：

1）建立了一种基于神经网络的弹道导弹落点预测模型。该模型以椭圆弹道落点预测偏差为输出，相比于直接以落点坐标为输出而言，网络结构大幅减小，同时，制导方法误差评价范围内的预测精度较高，3σ预测误差为4.97 m，实现了小网络模型对大范围飞行状态对应落点的预测。

2）为降低神经网络训练对显存需求量以及缩短训练时间，采用分块矩阵运算法则对LM 算法进行了改进，在并行学习策略设计的基础上，建立了一种IDP-LM 优化器。采用该二阶优化器进行训练后，训练耗时缩短约49.18%，且在一定程度上避免了显存不足问题的出现。

3）以STM32F407 单片机为实验平台，对预测算法复杂度进行了检验，仿真结果表明，预测实时性好，预测耗时为2.585 ms，其中，神经网络耗时为1.250 ms，椭圆弹道预测耗时为0.634 ms，其他耗时为0.696 ms。同时，本文方法在大范围飞行状态的预测问题中具有较大的潜力。

需要指出的是，本文仅考虑了对落点影响最大的J2项摄动和再入阻力因素，实际上，扰动引力、日月引力、太阳光压等因素对落点也有一定的影响。而考虑这些因素后，样本空间将成倍增加，对网络模型设计和训练方法提出了更高的要求。在本文建立的神经网络模型和IDP-LM 优化器的基础上，进一步研究针对上述落点影响因素的修正网络，将有助于提高工程应用性。