基于DDES 模拟的叶顶泄漏流与尾迹非定常干涉机理
李会,黄通,苏欣荣,袁新
清华大学 热科学与动力工程教育部重点实验室,北京 100084
涡轮叶片是航空发动机的重要热-功转换部件。叶顶泄漏流是涡轮动叶叶片通道内部的关键流动结构之一,其对涡轮叶片的气动损失、流动非定常性、高温部件可靠性等有明显影响。由于叶片两侧存在压差,导致流体在压力差驱动下从压力面侧经过叶顶间隙后流向吸力面侧,进而形成泄漏流。在黏性作用下,泄漏流在吸力面附近与主流掺混并卷吸形成泄漏涡,其引起的流动损失可以占到整个通道损失的30%甚至更高[1]。Denton[1]认为叶顶泄漏流产生的损失主要由3 部分组成,其中泄漏流在通道内造成的掺混损失为主要的损失来源。因此,深入开展叶顶泄漏损失产生机制方面的研究对于减少泄漏流带来的负面影响具有十分重要的理论意义。
叶顶泄漏流进入到主流通道后,会受到上游流动结构的影响从而产生非定常效应。Ameri等[2]采用数值方法研究了上游尾迹对下游叶顶间隙的传热影响,发现上游尾迹对下游叶片吸力面侧的压力分布产生的影响较小,但是会带来传热的非定常特性。刘火星等[3]采用实验方法研究了上游尾迹对叶栅通道内泄漏流的影响,发现上游尾迹使得下游通道涡区域损失减少,同时泄漏流损失也相应减少。Zhou K 和Zhou C[4]对比了雷诺时均Navier-Stokes(Reynolds Averaged Navier-Stokes, RANS)和非定常雷诺时均Navier-Stokes(Unsteady Reynolds Averaged Navier-Stokes, URANS)的结果,发现由于上游静叶产生的周期性尾迹的影响,下游动叶叶顶泄漏流造成的损失反而减小;之后他们通过实验改变上游尾迹达到了减少下游泄漏流损失的效果,进一步验证了该结论[5]。杨佃亮和丰镇平[6]通过施加非定常边界条件的方法,发现上游尾迹会对叶顶吸力面前缘附近和尾缘附近流场产生强烈的影响。
除了上游流场引起的非定常流动,在叶片通道内部叶顶泄漏流也会失稳并诱发较强的流场脉动。Gao 等[7]发现叶顶泄漏流向下游输运的过程中,在涡轮叶片吸力面侧逆压梯度的作用下,可能出现泄漏涡破碎现象,破碎后的流动呈现出明显的非定常特征。Sell 等[8]通过数值研究发现,在叶片近间隙吸力面侧后半部分存在回流区域,认为可能是叶顶泄漏涡破碎所致。Huang等[9]利用控制体模型方法研究了涡轮近叶顶负荷分布对泄漏涡动力学特性及损失的影响,研究发现,泄漏涡的稳定性受流向逆压梯度影响较大,流向逆压梯度足够大时会诱发泄漏涡破碎,带来额外的涡破碎损失。Yang 和Ma[10]使用数值模拟对一典型透平动叶泄漏涡的特征做了研究,结果表明逆压梯度导致涡核附近的雷诺正应力增强,进而造成泄漏涡破碎。以上研究都说明了泄漏流在向下游流动过程中自身存在着非定常特性,普遍的观点是由于逆压梯度的存在导致了泄漏涡破碎,但对于是什么流动结构引起的逆压梯度却缺乏分析和说明。
为了准确地模拟泄漏流复杂的流动现象,理论上只有采用直接数值模拟(Direct Numerical Simulation, DNS)方法和大涡数值模拟 (Large Eddy Simulation, LES) 方法。受限于高雷诺数流动中的计算量问题,DNS 和LES 主要用于简单几何和较低雷诺数泄漏流的机制研究。Shang等[11]使用DNS 对扁平水翼做了仿真,将泄漏涡分成了3 个阶段,即生成段、发展段、分裂破碎段。Gao 和Liu[12]采用了LES 方法对简化的泄漏流模型进行研究,并且获得了丰富的流场结构。目前高负荷透平通道内部流动分析主要采用RANS方法,其能够在耗费较少计算资源的前提下,快速给出流场的时均结果,但是该方法无法实现物理上多尺度湍流的精细模拟[13]。对于叶栅通道内部的三维尾迹涡结构、泄漏流非定常流动等复杂流动结构,RANS 方法存在局限性,进而导致复杂流动的机制研究受限。混合RANS/LES 方法能够以较小的代价实现对复杂几何、高雷诺数流动的高精度湍流模拟,可以较好地解决计算精度和计算资源之间的矛盾。Spalart[14]在1997 年发展了脱体涡模拟(Detached Eddy Simulation,DES)方法,DES 方法是一种将LES 和RANS 相结合的方法。DES 方法在近壁面边界层内采用非定常RANS 模型,在远离壁面的强剪切区域自动切换到LES 方法。为了改进DES 方法对应力模化的能力,2006 年Spalart 等[15]将DES 方法升级为延迟脱体涡方法 (Delayed Detached Eddy Simulation, DDES)。DDES 方法既能很好地模拟主流的湍流特性,又比LES 和DNS 方法极大地减少了计算时间。目前关于叶轮机械的计算已有很多DDES 算例,Lin 等[16]采用DDES 方法对高压透平级的非定常流动进行了分析;Bian等[17]对端壁流动的湍流特性分析也采用了DDES 方法;Wang 等[18]采用了DDES 方法对压气机的角涡分离和尾迹做了相关研究。然而目前还鲜有学者采用DDES 方法对叶顶泄漏涡和尾迹干涉的流动结构做精细模拟。对于泄漏涡破碎和与尾迹之间干涉的机制尚没有明确认识。
针对现有研究在叶顶泄漏流与尾迹干涉以及泄漏涡破碎方面研究的不足,采用DDES 方法研究某高负荷透平动叶叶顶间隙泄漏流以及下游尾迹涡的非定常特性。首先从叶顶间隙泄漏涡的演变、泄漏涡与端壁涡和尾迹涡的相互作用现象进行分析,说明泄漏涡破碎的机制;然后具体分析泄漏流与尾迹干涉机制;最后系统地分析泄漏流与尾迹干涉带来的流场损失特性,以期揭示其在二次流损失中的重要性。
1 数理模型
1.1 计算域与计算网格
所研究的计算模型为某高压涡轮动叶直列叶栅,叶顶间隙高度为叶片高度的1%。计算域如图1 所示(Ca为轴向弦长),进口马赫数为0.38,基于轴向弦长的雷诺数为2.93×105。图2为叶片表面和端壁上的计算域网格分布,还给出了前缘和尾缘处的网格细节。计算网格采用非结构网格,叶片表面上沿着流向方向有652 个网格点,间隙高度方向上布置了40 个网格点,壁面外第Ⅰ层网格点上的无量纲壁面距离y+≈1。基于RANS 计算结果和DDES 的初步计算结果对网格进行了多轮调整,主要加密了尾迹区和泄漏涡区域的网格点分布,以实现对小尺度流动结构的准确捕捉,最终使用的计算网格包含约1 400 万个网格单元。
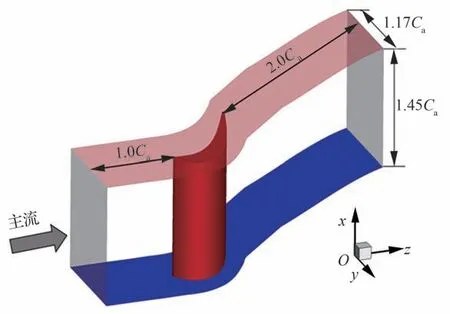
图1 计算域示意图Fig.1 Schematic diagram of computation domain
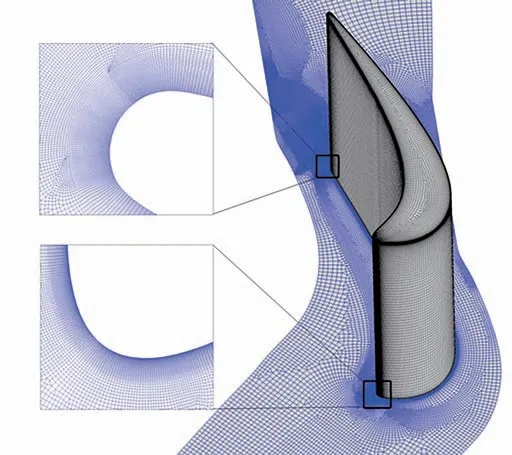
图2 计算域网格划分示意图Fig.2 Schematic diagram of computation domain mesh
1.2 数值方法
DDES 计算采用自主开发的多块并行有限体积代码[19-22],所求解的积分形式Navier-Stokes方程为
式中:τ0为虚拟时间;U为N-S 方程的守恒形式自变量;V为网格单元的体积;t为物理时间;Fc为对流通量;Fv为黏性通量;n为积分面积法向量;S为积分面积分别表示虚拟时间项、物理时间项和空间残差项。
在计算中,采用双时间步方法进行非定常计算,且物理时间项采用隐式四点二阶方法进行离散。为尽可能减小数值耗散对流动结构模拟结果的影响,数值模拟中采用5 阶WENO 格式和自适应低耗散格式[16],进一步降低数值黏性、提高对小尺度流动结构的解析精度[23]。为了加快每个物理时间步内的收敛速度,程序中对虚拟时间项采用了隐式时间推进方法进行求解。为了进一步加速收敛,还采用了多重网格方法。在之前的研究工作[24]中已对数值方法进行了实验验证工作,验证了该数值方法的有效性。
为了准确捕捉高频、小尺度非定常流动结构,通过对泄漏涡区域非定常特性的分析,确定非定常计算中的物理时间步长为2.5×10-6s,以确保能准确计算高频非定常流动结构。图3 给出了计算过程中连续7 个物理时间步内的收敛情况。从图3 中可见,每一个物理时间步约需内部迭代30 步后,残差可降低3 个数量级。从图4 尾迹区的监测点可以看出,非定常流场计算已经进入统计平均收敛阶段,可以对非定常流动计算结果进行分析和统计平均。
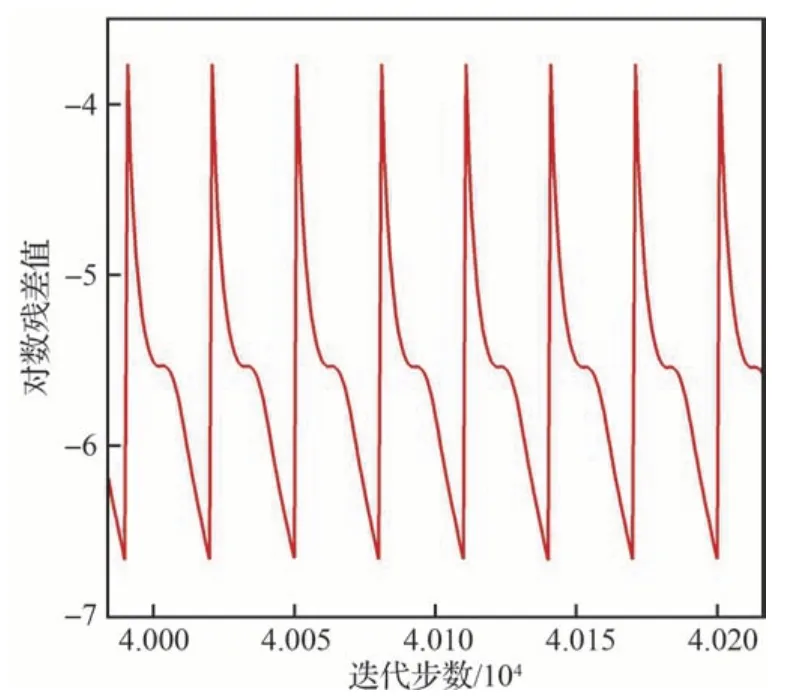
图3 非定常求解收敛历史Fig.3 Convergence history of unsteady simulation
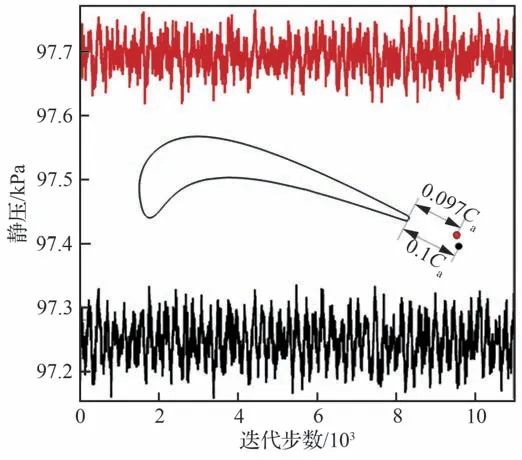
图4 监测点压力分布Fig.4 Pressure distribution at monitoring points
2 泄漏区非定常特性
在DDES 方法中,边界层内使用RANS 模型,而在远离壁面区采用LES 方法。除了基于y+等参数来判断边界层内部网格的密度外,还需要判断主流区网格密度是否合适。采用湍动能模化率指标来判断主流区的网格分辨率是否满足LES 求解要求。湍动能模化率IQ 的定义为
式中:Eslov为通过直接求解解析得到的湍动能;Esgs为亚格子应力模化得到的湍动能。通常认为大涡模拟需要解析80%以上的湍动能,才能解析得到大部分湍流成分[25],从图5 中可以看出,主流区的湍流模化率均在80%以上,说明主流区基本解析到了大尺度湍流结构,满足LES 对网格分辨率的要求。
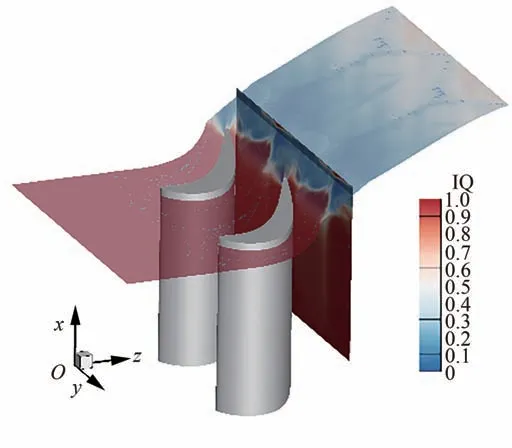
图5 湍动能模化率分布Fig.5 Contour of index of resolution quality
此外,还在中叶展的尾迹涡区域、叶顶间隙内的泄漏流分离泡和端壁涡区域分别设置了监测点,对监测点速度进行傅里叶变换并得到功率谱密度图(Power Spectral Density, PSD),如图6所示,可以看出DDES 计算结果在惯性子区很好地满足了-5/3 次方率,这一结果也可以从侧面验证该数值方法的有效性。图7 展示了泄漏涡、尾迹涡、尾迹与泄漏涡干涉区域最大幅值对应的频率,其中U、V和W分别为3 个方向上的速度分量。可见泄漏涡与尾迹涡最大幅值对应的频率相同,均为1 800 Hz,且尾迹涡的幅值小于泄漏涡的幅值。从图7(c)中可以看出,在尾迹与泄漏涡相互作用区域,除了1 800 Hz 的频率外,还出现了更高的倍频,这是两种涡系干涉后产生的破碎涡系的频率,此时干涉区的幅值也有明显增大,说明泄漏涡与尾迹涡之间具有很强的非定常干涉作用。
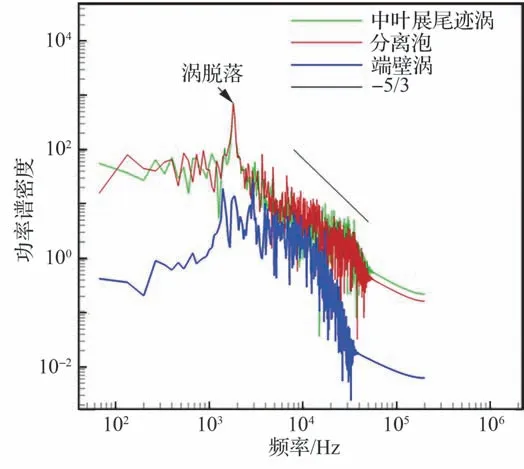
图6 监测点速度功率谱密度分布Fig.6 Velocity power spectral density distributions at monitoring points
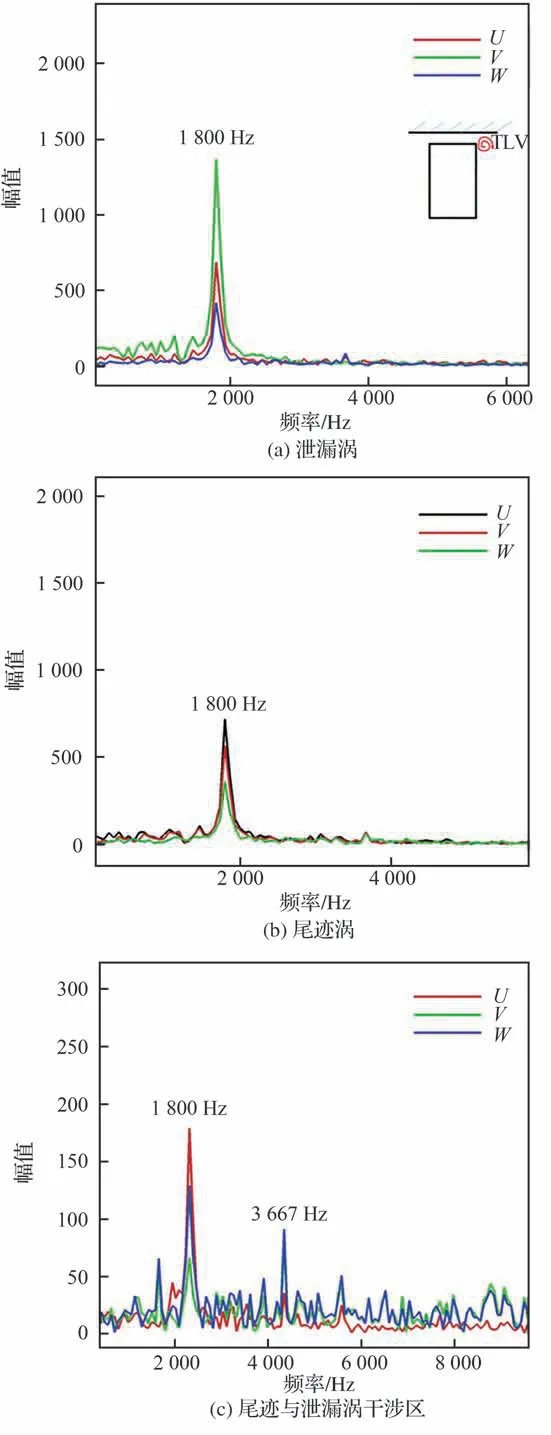
图7 不同位置处最大幅值对应频率Fig.7 Frequencies corresponding to maximum amplitude at different positions
2.1 叶片表面压力系数分布
图8 展示了50%和95%叶高截面上的压力系数分布。图8(a)中h为叶片高度;z为轴向位置;Cp为压力系数。由图8(a)中可以看出,50%叶高和95%叶高的压力面侧压力系数分布基本重合,意味着泄漏流对叶片压力面侧的载荷分布几乎不产生影响。图8(b)中y为展向位置。从图8(b)和图8(c)中可以看出,叶片不同高度下压力面侧的云图分布也基本一致。但是在不同叶高下,吸力面侧的压力系数分布在约10%~90%轴向弦长范围内存在差异。在95%叶顶高度处,吸力侧受到泄漏流的影响更为严重,因此产生了相较于50%叶顶高度处的压力系数分布差异。顺着流向方向,随着泄漏流不断增强,吸力面侧的压力系数差异也随之逐渐增加。在60%轴向弦长以后,由于泄漏流逐渐远离叶片吸力面侧,其对吸力面侧压力的影响也逐渐减小。可见泄漏流对叶片表面载荷的分布具有较大的影响。
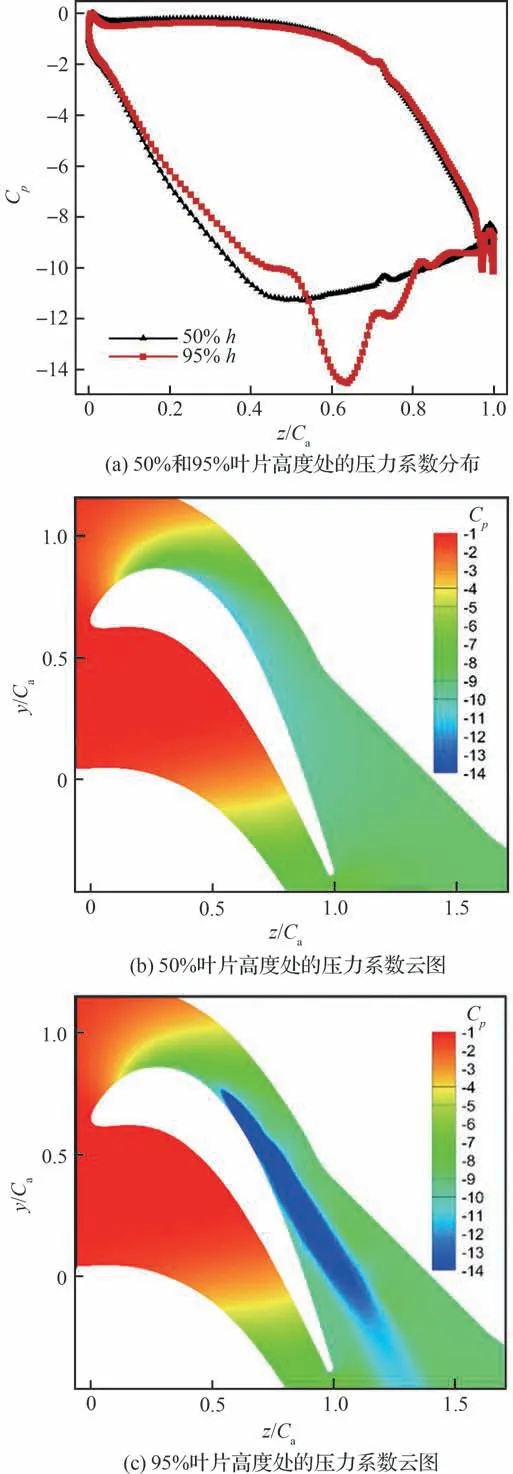
图8 叶片表面和叶栅通道压力分布Fig.8 Load distributions of blade surface and cascade passage
2.2 流动结构分析
图9 为叶顶泄漏流时均流场结果,用Q准则表达涡结构,并用无量纲流向涡量系数进行染色。Q准则的定义是速度梯度的第二不变量,当Q大于0时表示流体中旋转程度大于变形程度,认为该区域中存在涡。无量纲流向涡量系数的定义为
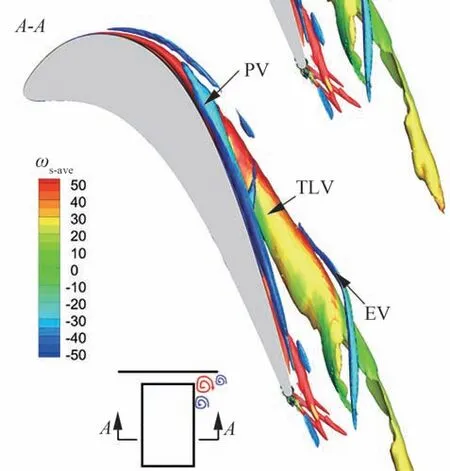
图9 时均流场涡结构(Q=1×108 s-2)Fig.9 Time averaged flow field vortical structures (Q=1×108 s-2)
式中:Ω为涡量;u为速度;l为特征长度,此处选为轴向弦长;uin为进口速度大小。
为了方便展示流场中的涡结构,视图选择了从叶根朝向叶顶方向的视角。从图9 中可以明显地分辨出叶顶泄漏涡(TLV)、通道涡(PV)和端壁涡(EV)。在泄漏涡往下游发展过程中,端壁涡开始缠绕在泄漏涡周围,使得泄漏涡出现不稳定现象,并使得泄漏涡的完整性被破坏。通道涡被泄漏涡挤到叶顶下方,然而其与泄漏涡互不干涉。在时均流场中,由于时间平均的作用,只有大尺度的涡结构保留下来,观察不到小尺度的涡结构。为了探究叶顶区域的非定常特性,需要对瞬时流场做进一步分析。
选取了某一时刻的瞬时非定常流场进行分析,如图10 所示。相较于时均流场,瞬时流场中包含更为丰富的小尺度涡结构。在端壁涡与泄漏涡相互作用之前,泄漏涡和通道涡以及端壁涡的结构与时均流场一致,这意味着这些涡结构在相互作用之前都保持稳定和近似定常的状态。在瞬时流场中可以发现端壁涡和泄漏涡相互作用后泄漏涡被破坏,产生一系列诱导涡(IV)。尾迹涡(WV)从尾缘处脱落并向下游输运,在输运的过程中可以发现诱导涡与尾迹涡发生相互干涉。尾迹涡受到诱导涡的干涉后,尾迹涡也破碎成更小尺度的涡结构并往下游输运。可见泄漏涡、端壁涡和尾迹涡之间相互作用使得叶顶区域的流场出现很强的非定常性。
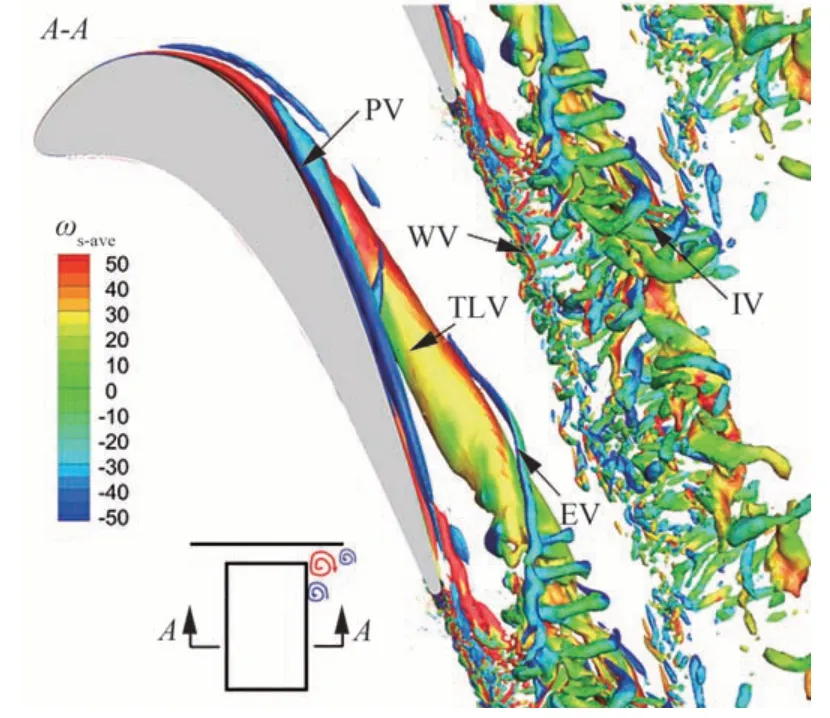
图10 瞬时流场涡结构(Q=1×108 s-2)Fig.10 Instantaneous flow field vortical structures (Q=1×108 s-2)
2.3 泄漏涡与尾迹干涉机制
为了更好地说明泄漏涡与端壁涡,以及其和尾迹涡间的作用过程,图11 给出了尾迹涡脱落周期内(周期为τ)的4 个典型时刻。红色虚线圆圈表示泄漏涡和端壁涡相互作用产生的诱导涡,从图11(a)到图11(d),该涡逐渐向下游输运。红色实线表示泄漏涡与尾迹相互干涉区尾迹涡的轨迹,红色箭头表示尾迹摆动的方向。在(1/4)τ时刻,泄漏涡和端壁涡相互作用后,诱导涡开始产生。此时从尾缘脱落的尾迹涡也开始向下游移动。到了(2/4)τ和(3/4)τ时刻,诱导涡继续向下游传播,并且泄漏涡和端壁涡相互作用产生的新的诱导涡也开始从上游往下游传播。此时之前上游产生的诱导涡还没有和尾迹涡发生干涉。到了(4/4)τ时刻,从纹影图中可以看到诱导涡和尾迹涡相互作用,流场变得更加无序,并且涡结构的完整性遭到破坏。从不同时刻的纹影图中还可以看出尾迹涡的运动轨迹也受到诱导涡系的影响,发生了明显的左右摆动。
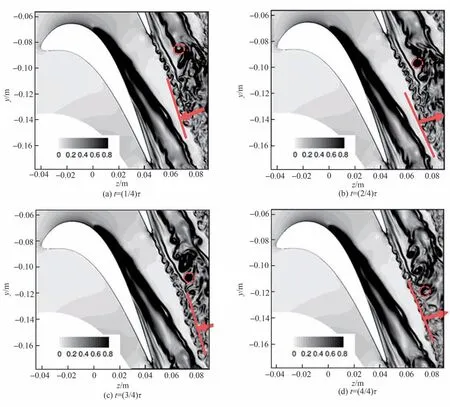
图11 95%叶高处密度梯度纹影图Fig.11 Contour of density gradient magnitude at 95% blade height
通过对非定常计算结果进行后处理,可以计算得到湍动能。图12(a)为95%叶高截面上泄漏区与尾迹区的湍动能分布。从图12(a)中可以看出:在此截面上,湍动能最大的区域不是尾迹区和泄漏流区域,而是泄漏流和尾迹涡发生相互干涉的区域。截取从尾缘到下游泄漏流与尾迹干涉区,并作周向平均得到图12(b)。从图12(b)中可以看出,从尾缘往下游移动的过程中,湍动能呈现先增加后减小的趋势。这是因为随着端壁涡与泄漏涡相互作用产生的拟序结构使得流场中的湍动能逐渐增加,在泄漏涡与尾迹涡发生干涉的区域湍动能达到了最大,随着干涉后产生的涡破碎,湍动能逐渐耗散,导致湍动能逐渐减小。
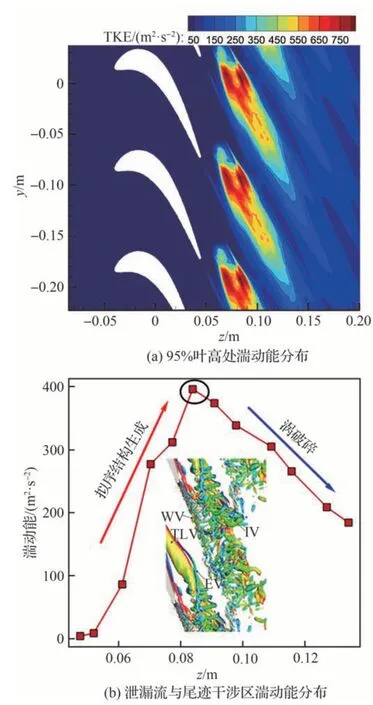
图12 湍动能分布Fig.12 Turbulent kinetic energy distribution
3 泄漏区非定常损失机制
从热力学的角度来看,流场中的不可逆性是损失的来源,其可以分为两类:由流体黏性引起的不可逆损失和由传热过程引起的不可逆损失。在目前常用的损失分析方法中,总压损失系数、熵增等指标只能反映定常流场中总的损失情况,无法明确给出流场中损失生成的位置和强度,且其应用于非定常流场时常出现损失系数小于0 或者大于1 等非物理的情况。因此采用熵生成率对叶顶区域的时均和瞬时流场进行分析,非定常的熵输运方程形式为[26]
式中:ρ为密度;s为熵;uj为速度分量;T为温度;xj为某方向上的分量;τij为黏性应力张量分量;Sij为应变率张量分量;λ为导热系数分别表示由流体黏性引起的熵增和由传热引起的熵增。在相关研究中[16,27],发现由传热引起的不可逆性损失占比很小,损失主要为黏性引起的不可逆性损失,因此重点分析黏性不可逆性损失。黏性耗散引起的熵生成率为
与图11 中4 个物理时刻相对应,图13 给出了相应的黏性损失熵产率分布。从黏性耗散的云图中可以看出,不同时刻下的黏性耗散除了发生在上游泄漏涡和端壁涡所处的位置,在下游泄漏涡和端壁涡相互作用的位置也出现了很强的黏性耗散。在(4/4)τ时刻,诱导涡和尾迹涡发生相互作用的区域,也可以看到黏性耗散增强。通过比对时均结果和瞬时结果的黏性耗散云图可以看出,泄漏涡和端壁涡以及尾迹涡相互作用增强了流场的非定常性,并且带来了黏性耗散损失。
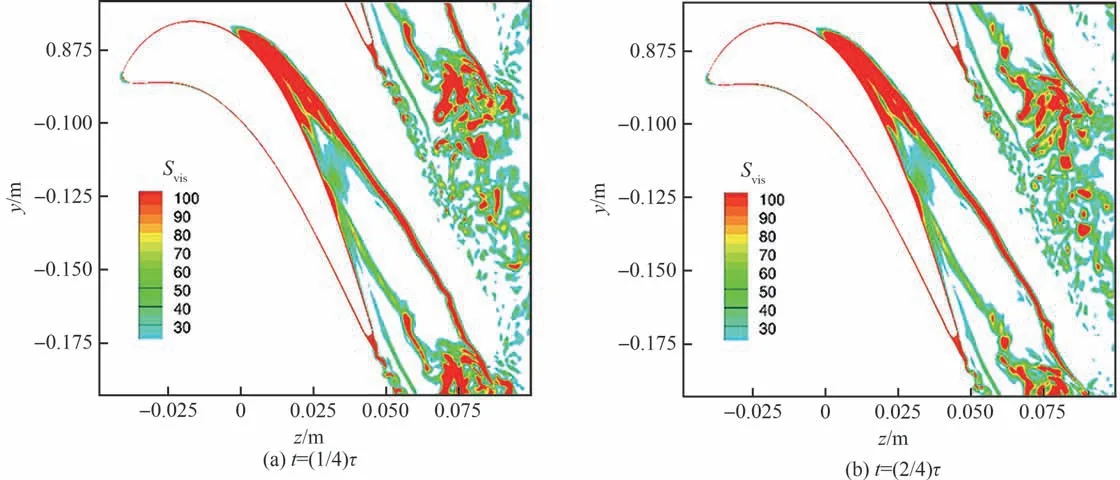
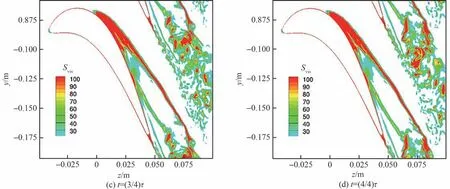
图13 不同时刻的黏性耗散损失分布Fig.13 Distributions of viscous dissipation loss at different times
图14 选取了130%Ca截面,得到了3 个周期内的瞬时黏性耗散引起的熵生成率(红色方块)、时均流场黏性耗散引起的熵生成率(绿色实线)、时均流场总的熵产率(黑色实线)。从图14 中可以看出,对于黏性耗散而言,瞬时流场下的结果大于时均流场下的结果,损失偏差最大为71%。这意味着泄漏涡和端壁涡以及尾迹涡相互作用导致的非定常损失不可忽略。从不同时刻的损失分布可以看出,损失出现周期性,这也说明了叶顶泄漏区的流动具有很强的非定常性。时均流场总的熵产率包括由黏性耗散引起的和由小尺度脉动引起的,定义小尺度脉动引起的熵产贡献为时均流场下总的熵产率和黏性耗散的熵产率的差值,即
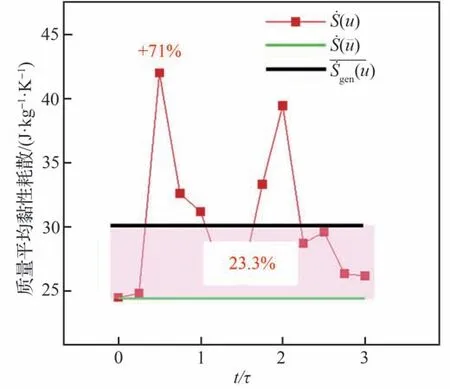
图14 130% Ca轴向截面处的黏性耗散损失分布Fig.14 Distribution of viscous dissipation at 130% Ca axial section
由小尺度脉动引起的熵产如图14 中粉色部分所示。可以发现,泄漏流与尾迹干涉区产生的小尺度脉动熵产贡献占到时均流场总熵产的23.3%,占比较大,是不可忽略的一部分。这说明泄漏流与尾迹相互干涉产生的非定常损失是高压透平叶顶泄漏流损失中的重要来源之一。因此对于叶顶泄漏流损失的研究,如果仅使用RANS 方法,仅能得到时均下的流场损失结果,对实际的损失估计不足,建议采用DDES 方法等可以得到瞬时流场且精度更高的方法。
4 结 论
使用DDES 方法对涡轮动叶叶顶间隙泄漏流进行数值模拟,并分析了泄漏涡与端壁涡、尾迹涡之间的干涉作用,最后分析了泄漏流区域的损失机制,得到如下结论。
1)DDES 方法可以精细地捕捉到泄漏涡和尾迹涡等涡结构,以及各种涡系相互作用产生的更小尺度的涡结构,对于分析叶顶泄漏流等复杂涡系之间的作用机制,可以很好地平衡计算代价和计算精度之间的矛盾。
2)叶顶泄漏涡在发展过程中会首先与端壁涡产生相互作用,泄漏涡出现不稳定现象,继而发生破碎,并周期性地产生诱导涡;诱导涡在下游会与尾迹涡产生干涉作用,使得尾迹涡的轨迹出现周期性左右摆动,并破碎成更小尺度的涡系结构,并逐渐耗散成无序涡结构。涡系之间的相互作用具有很强的非定常性。
3)基于非定常熵输运方程,得到了流场黏性耗散带来的熵增,其中瞬时流场下的损失大于时均流场下的损失,最大偏差可达到71%,说明非定常流动带来的损失不可忽略。由小尺度脉动所产生的损失,可以占到时均流场总损失的23.3%,是非常重要的损失来源之一。对于高效透平叶栅设计,需要考虑非定常流动带来的损失,以进一步提高透平性能。

