大型复合材料机身壁板多机器人协同装配调姿控形方法

杨应科，李东升，沈立恒，李汝鹏，翟雨农，3，*

1．北京航空航天大学 机械工程及自动化学院，北京 100191

2．中国商飞上海飞机制造有限公司，上海 201324

3．北京航空航天大学 宁波创新研究院，宁波 315800

飞机机身壁板是构成飞机气动外形与骨架的关键零部件，在装配过程中需要严格保证其位姿与形状的装配精度［1］。机身壁板作为大尺寸薄壁件，易发生变形，因此需要多台定位器同时夹持，通过协同运动调整其空间位姿并控制外形。在新一代大型客机机身结构设计中，大量采用了具有高比强度和比刚度、优异的耐疲劳和耐腐蚀性能以及独特的力学性能可设计性的复合材料壁板［2］以减轻结构重量、提高结构寿命、降低制造成本。例如空客A350 系列机身均采用复合材料壁板，全机复合材料用量达54%［3］。由于在材料、结构及制造工艺方面的差异，相比于金属机身壁板，整体成型的复合材料机身壁板尺寸更大，且复合材料层合板结构易受力发生损伤［4］，其装配过程中对装配力水平要求更为严苛。因此，复合材料机身壁板装配对多定位器的协同运动控制要求更高，导致其装配难度更大。

当前，国内外航空制造商主要使用笛卡尔三自由度柔性数控定位器进行飞机装配。该定位器可沿3 个相互正交的方向做平移运动，其顶端有球铰式工艺接头与部件进行连接，通过多台定位器与部件组成并联机构以调整部件位姿［5］。这种定位器使得装配工装的数量大幅减少，从而缩短了工装准备周期并且提高了装配效率［6］。波音公司在B737 NG、B777 等系列客机机身装配过程中均使用了三自由度柔性定位器［7］。空客公司采用多台三自由度定位器组成的多点式柔性工装完成A350 XWB 机身壁板装配，通过多台定位器的同步协同运动来调整壁板在三维空间中的位姿［8］。国内C919 客机在机身壁板装配与机身筒段对接时也使用了三自由度数控定位器。

国内外学者围绕三自由度定位器开展了大量研究工作。Schneider［9］提出了基于三自由度定位器的模块化柔性飞机大部件定位系统。Huang 等［10］设计了基于视觉定位的三自由度定位器对接装配系统。Mbarek 等［11］建立了外载荷和温度变化条件下定位器理论位置与偏差的关系模型，利用逆运动学计算修正量。Bi 等［12］基于三自由度定位器研究了机身壁板的装配变形预测与校正。Chen 等［13］研究了基于确定性理论的飞机大部件装配最佳拟合定位，并应用于三自由度数控定位系统。Deng 等［14］考虑了飞机大部件重力变形，研究了三自由度定位器球铰定位的不确定性评估以及在线校准。Mei 等［15］利用有限元模型分析温度与重力对数控定位器基准的影响，并对其加以修正以提高翼盒调姿的精度。邱宝贵等［16］设计了基于三自由度定位器的机身调姿与对接系统，并通过有限元分析装配对接过程中多轴运动协同误差对部件的影响。郭志敏等［17］建立了定位器受力变形与飞机大部件姿态误差的关系模型，实现了飞机大部件调姿中位姿精度补偿。黄翔等［18］针对基于三自由度定位器的对接装配系统提出了飞机大部件对接装配轨迹规划方法。陈文亮等［19］根据Clamped-Free 变形协调原理，简化了机身壁板装配过程中定位器调姿内力之间的协调关系，并提出了重力前馈补偿和调姿内力转化为位置补偿的力位协同控制策略。基于笛卡尔三自由度定位器的柔性装配方法可实现机身壁板的精准调姿与定位，但由于各定位器末端球铰接头为被动旋转副，存在一定量的驱动误差，会影响调姿过程中多定位器的协同运动精度，易造成复材壁板拉扯甚至损伤；此外，对于壁板形状调整而言，定位器三向平移驱动的主动调整能力有限。因此，基于笛卡尔三自由度定位器的柔性装配方法对于大尺寸复合材料机身壁板调姿控形存在一定缺陷与不足。

多自由度驱动的并联机器人能主动控制其末端平移与旋转，同时也具备较高的精度与较强的承载能力，这为实现更高精度的多定位器协同运动提供了新思路。因此，多自由度并联机器人被越来越多的飞机装配领域学者和研究机构所关注。Jonsson 和Ossbahr［20］基于六自由度并联机器人Flexpod 提出一种经济型可重构柔性工装，通过外部测量设备调整，其无需高精度支撑框架即可达到较高的定位精度。Ramirez 和Wollnack［21］研制了基于工业并联机器人的柔性自动装配系统用于复合材料壁板装配。Reid［22］提出一种基于六自由度并联机器人的移动式装配装备并用于波音公司飞机机翼装配。Bertelsmeier 等［23］基于力控制原理，使用三台协作机器人控制复合材料壁板变形。Qu 等［24］针对壁板类部件设计了基于并联构型的五自由度柔性定位机器人并对驱动配置进行了优选。王伟等［25］提出了一种基于3-UPS 并联构型的飞机装配调姿定位机器人，同时分析了铰链间的误差间隙对精度的影响。文科等［26］在六自由度调姿平台上开展了舱段类部件数字化柔性对接试验研究。上述研究主要关注单台并联机器人的运动控制与定位精度，对于装配过程中的多机器人协同运动研究还较少。

在装配过程中，飞机机身壁板通过多定位器的协同运动实现空间中的位姿调整，因此，需构建壁板空间位姿调整量与各定位器驱动量的运动传递关系。相比于三自由度定位器，多自由度定位器本身机构形式更加复杂，使得冗余驱动自由度更多，基于三自由度定位器的调姿控形方法不再适用。因此，为了实现基于多自由度机器人的复合材料机身壁板多机协同装配，解决三自由度定位器感知与调控能力有限的问题，实现复合材料机身壁板调姿控形一体化。

以多机器人柔性装配工装为研究对象，建立了该工装的全局运动学模型。采用基于主从协同运动的调姿方法，并给出了协同运动误差分析。构建了复合材料机身壁板形状偏差与机器人运动量的变换关系，利用机器人运动控制壁板变形。通过具体应用实验验证了本文方法的有效性。

1 复合材料壁板多机器人柔性装配工装

典型复合材料机身壁板结构如图1 所示，复合材料蒙皮与长桁共固化成型，成型后的壁板再通过角片与高锁螺栓同隔框进行连接。用于飞机复合材料机身壁板装配的多机器人柔性装配工装主要由支撑框架、并联机器人、真空吸盘夹持单元、激光跟踪仪以及集成控制系统组成，如图2 所示。

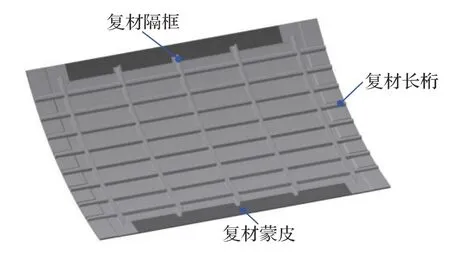
图1 复合材料机身壁板Fig.1 Composite fuselage panel

图2 复合材料机身壁板多机器人柔性装配工装Fig.2 Multi robotic flexible assembly system for composite fuselage panel

作为工装的执行机构，六足并联机器人可以实现X、Y、Z轴3 个正交方向的平移与旋转。其末端夹持单元带有多个真空吸盘，呈等边三角形布局。吸盘内部设计有限位结构，可实现对不同曲率复合材料机身壁板的稳定吸附夹持并约束其外形，在测量标定过程中，限位结构上的限位块可更换为反射靶球，以测量机器人末端夹具夹持接触点位置。夹持单元下方安装的力/力矩传感器可实时监测装配过程X、Y、Z轴3 个方向上的力与力矩。通过多组并联机器人的组合式排列，装配工装可完成不同尺寸的复合材料机身壁板的装配任务：多机器人高精度协同运动完成壁板的整体位姿调整；单个机器人末端的平移与旋转可以实现对局部区域的外形调控。装配过程中，传感器监控夹持点装配力与装配力矩，确保复合材料机身壁板在调姿控形过程中不发生内应力超差而导致壁板损伤，保证装配性能与装配质量。

2 基于多机器人的调姿控形方法

传统的数控定位器多为三自由度主动驱动，其末端为球铰，可进行自由旋转，运动学模型相对易于构建。而机器人为六自由度全主动驱动，多机器人协同的运动学模型更加复杂。因此需要构建精确的多机器人柔性装配工装的全局运动学模型，采用主从协同控制方法实现壁板调姿过程中多机器人的协同运动，并基于运动学模型与壁板形状误差求解各机器人驱动量，实现复合材料机身壁板形状控制。

2.1 机器人夹持单元预定位

装配工装中各坐标系定义如下，如图3 所示，其中，SW为世界坐标系；SLT为激光跟踪仪坐标系；SBi为第i个机器人的基座坐标系；SFi为第i个机器人的法兰中心坐标系；SCPi为第i个机器人的接触点坐标系；i={1，2，…，N}，N为机器人数量。

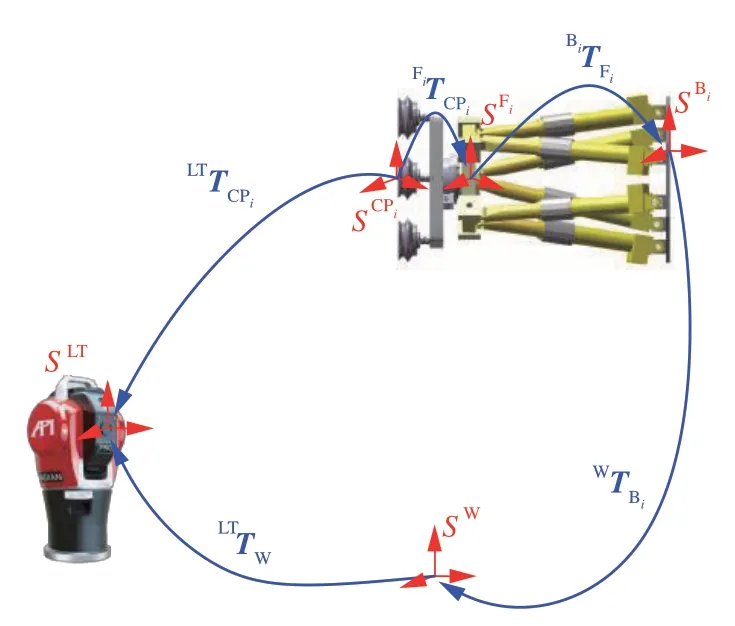
图3 装配工装系统坐标系定义Fig.3 Definition of coordinate system in assembly system

定义任意坐标系S2相对于坐标系S1的齐次变换矩阵为

复合材料机身壁板曲率较大，真空夹持单元为实现对复合材料机身壁板稳定吸附夹持，各真空夹持单元接触点需要在三维空间中预先定位，形成机身壁板外表面形状轮廓，夹持单元的法向适应壁板曲率，否则可能会造成损伤壁板。通过激光跟踪仪测量夹持单元上3 个吸盘内部的限位结构上的靶球即可定义接触点坐标系SCPi，定义夹持单元的初始吸附夹持位置即计算接触点坐标系SCPi相对于壁板坐标系SP的变换关系PTCPi。

采用等效圆柱几何模型实现夹持单元接触点预定位，接触点对称分布于壁板外表面，如图4所示。在壁板坐标系SP的Oyz平面内，定义矢量其分量作为接触点的y、z坐标，则有

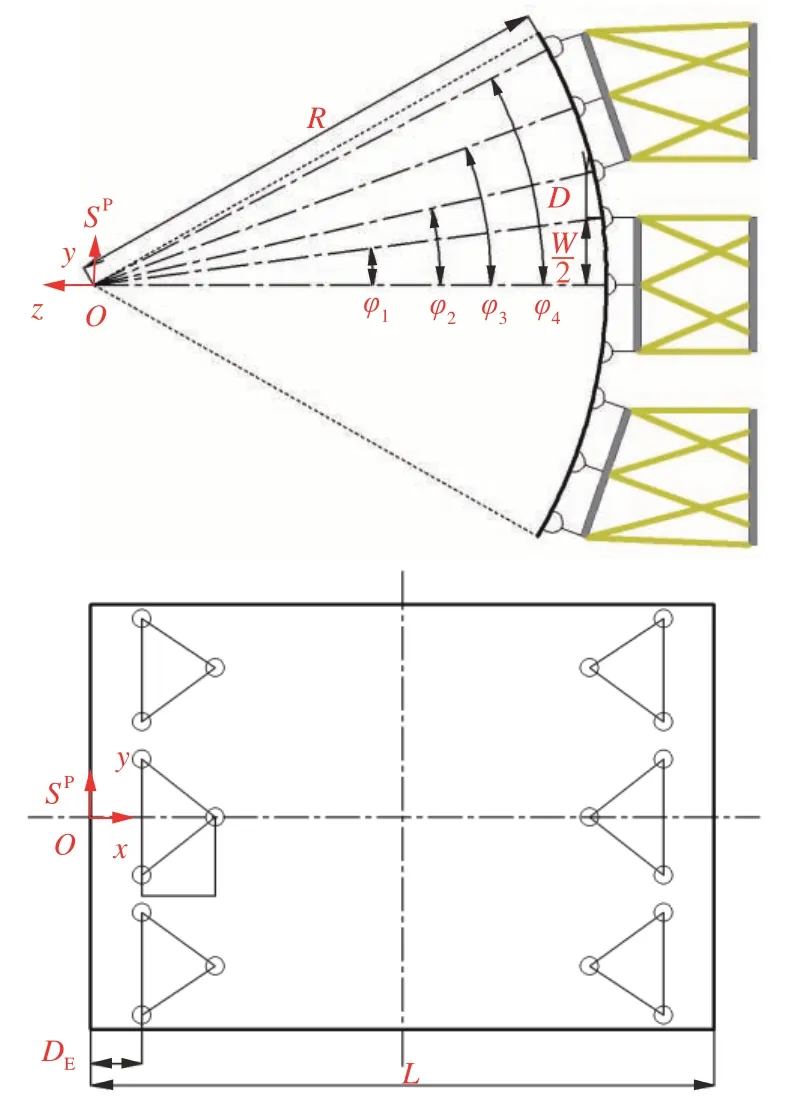
图4 夹持单元接触点分布Fig.4 Distribution of fixture contact points

式中：R为复合材料机身壁板等效半径；φi为夹角，其计算公式为

式中：W为夹持单元宽度；D为两个夹持单元接触点间的间距。

在坐标系SP的Oxy平面内，定义接触点距离分量，j={1，2，3，4}，则有

式中：DE为夹持单元与壁板的边缘间距；H为夹持单元高度；L为壁板长度；θ为接触点所在平面与壁板轴线方向的夹角，如图5 所示，则有

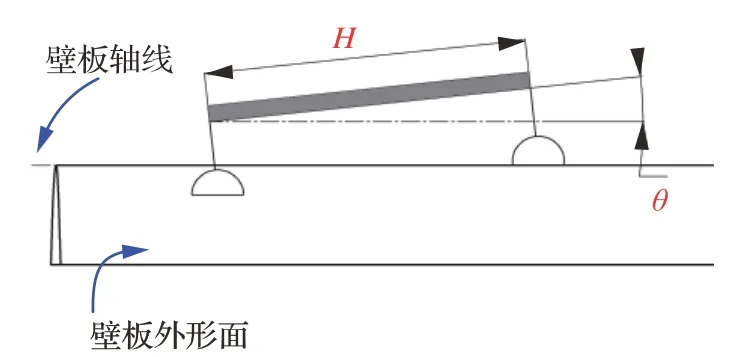
图5 夹持单元俯视图Fig.5 Top view of clamping unit

由此，夹持单元各接触点在坐标系SP的位置可由vi与xj表示。利用三点法定义接触点坐标系SCPi，即可计算SCPi与SP的变换关系PTCPi。机器人预定位驱动量则有

式中：WTP与PTCPi可通过激光跟踪仪测量获取，而WTBi与FiTCPi则需要通过对基座等坐标系的标定［27］，建立装配工装全局运动学模型求解。

2.2 装配工装全局运动学模型

装配工装各坐标系之间可建立运动学方程

式中：LTTCPi与LTTW可通过激光跟踪仪测量获得，机器人控制器可直接读取BiTFi，而FiTCPi和WTBi是未知的。因此装配工装全局运动学模型构建的核心就是辨识变换矩阵FiTCPi与WTBi。其辨识精度直接决定了全局运动学模型构建的精度。

采用解析法［28］求解未知变换关系FiTCPi，再代入式（7）中获得WTBi。如图6 所示，对于第i个机器人，其法兰中心点做相对运动，从初始位姿SFi0运动到目标位姿SFi1，可构建运动方程：

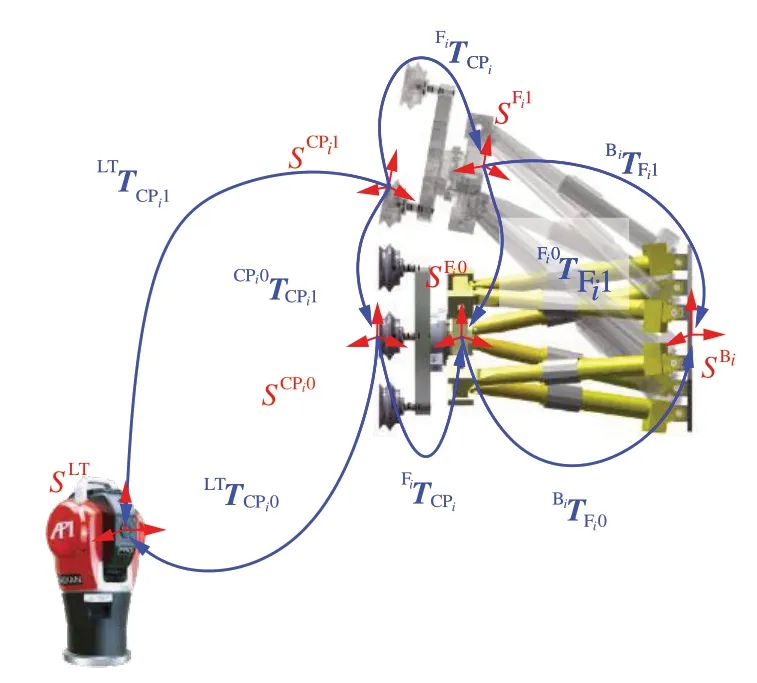
图6 单次相对运动中坐标系变换Fig.6 Transformation of coordinate system with one relative motion

在运动过程中，FiTCPi为未知常量，Fi0TFi1与CPi0TCPi1可通过激光跟踪仪与机器人控制器获取，可得

式中：

将式（10）改写为线性方程组，得

式中：矩阵M与向量y由Fi0TFi1与CPi0TCPi1中元素组成。

为了求解FiTCPi并减小由于测量等因素引入的随机误差，引入n次线性无关的相对运动，扩展式（12）为

令ri(x)=Mi x-yi，设

式中：r(x)=(r1(x)，r2(x)，…rn(x))T。

线性方程组式（13）的求解问题转化为最小二乘问题，即

采用相应的解析解法或数值计算方法可求解x，即FiTCPi，再代入式（7）中，可获得未知变换关系WTBi。至此，装配工装的全局运动学模型及各坐标系变换关系构建完毕。

2.3 基于主从协同运动的调姿方法

在机身壁板调姿过程中，多台机器人需要协同运动，调整壁板的位置和方向。协同运动的误差可能会导致机器人之间发生拉扯，使壁板内部产生过应力甚至损坏。采用主从协同控制策略，它基于主、从机器人之间的运动学关系实现同步运动，在运动过程中，主机器人作为其它从机器人运动的参考，每个从机器人跟随主机器人运动，各机器人接触点坐标系之间的变换保持恒定。

2.3.1 主从协同控制调姿原理

主机器人与从机器人之间的坐标系变换关系在调姿开始前确定，由式（7）可根据世界坐标系SW计算第i个机器人的基座坐标系SBi，在主从协同运动中需要主机器人和每一个从机器人之间的相对变换，即主机器人基坐标系SBM在每个从机器人基坐标系SBiS下已知，则有

式中：BiSTBM为由主机器人基坐标系到第i个从机器人基坐标系的变换关系，如图7 所示。

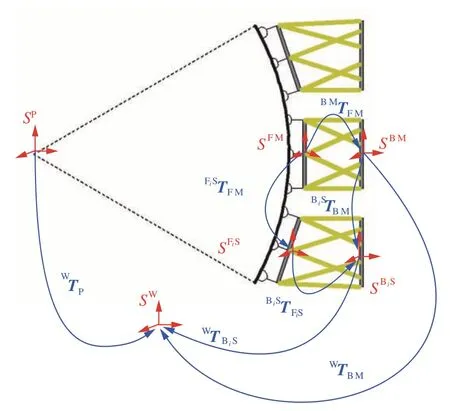
图7 主从机器人法兰中心坐标系变换Fig.7 Transformation between flange center coordinate systems of master and slave robots

由此，主机器人法兰中心坐标系和从机器人法兰中心坐标系之间的变换关系为

复合材料机身壁板通过真空吸盘固定在夹持单元上后，使用激光跟踪仪测量壁板上的靶标，建立壁板坐标系SP，其相对于世界坐标系SW的变换关系则有

式中：LTTP为壁板坐标系相对于世界坐标系的变换关系，由激光跟踪仪测得。

根据已知关系，可计算出壁板坐标系SP相对于主机器人接触点坐标系SCPM的变换关系CPMTP，它在壁板调姿过程中应始终为常数。然后将壁板坐标系的实际位姿ASP与目标位姿TSP进行比较，计算主机器人的相对运动量，最后主机器人进行相对运动，各从机器人跟随主机器人进行协同运动，进而完成壁板调姿。

在整个协同运动过程中，通过保持各接触点坐标系间的相对位姿不变，可避免复合材料机身壁板在调姿过程中产生过应力。

2.3.2 主从协同运动误差分析

在协同运动过程中，各从机器人的位姿完全由主机器人位姿与变换关系确定

将式（19）展开得

当主机器人进行纯平移运动时，旋转矩阵为单位矩阵E。此时从机器人相对运动则有

从机器人的平移量可表示为

从式（21）与式（22）可以看出，主、从机器人基座的相对方向以及法兰中心的相对方向在运动学模型建立过程中出现误差会导致主从协同运动产生误差，其中位置误差随机器人的移动距离增大而增大，而方向误差仅取决于全局运动学模型建立时的误差。

当主机器人进行纯旋转运动时，位移矢量BMtFM为0。此时从机器人相对运动则有

从机器人的平移量为

由式（23）与式（24）可知，主从协同运动误差除了与主、从机器人基座以及法兰中心相对方向误差有关外，还受到主、从机器人法兰中心相对位置误差等的影响。并且，协同运动误差与旋转运动量之间的关系更加复杂。

2.4 壁板形状控制方法

在装配过程中，复合材料机身壁板可发生一定的弹性变形，而在机器人夹持单元的夹持区域壁板刚性较强。利用这种整体弹性、局部刚性的特点来控制壁板变形，以满足复合材料机身壁板后续拼接时的外形精度要求。

壁板作为连续曲面，可通过离散的关键特征点表征外形。因此，在壁板内形面夹持单元附近刚性强的区域选取形状控制点，借助内形面形状控制点表征壁板的形状偏差，建立壁板形状偏差与各机器人运动量的变换关系，并通过机器人运动使复合材料机身壁板外形达到形状精度范围内。

如图8 所示，内形面形状控制点与对应的机器人法兰中心坐标系关系有

图8 壁板变形控制Fig.8 Shape adjustment of panel

建立内形面形状控制点实际位置SCiA 与目标位置SCiT 间的误差关系，然后转换为法兰中心调整量

变形控制采用迭代的方式进行，直至各形状控制点位置偏差均收敛到公差范围内。

3 应用实验验证

为了验证多机器人协同装配调姿控形方法的可行性，以复合材料机身壁板等比例试验件为对象，开展壁板位姿与外形调控实验，如图9 所示。该复合材料机身壁板外半径为2 960 mm，展向跨度为2 048 mm，航向跨度为3 100 mm，共有8 根复合材料长桁。实验所使用的激光跟踪仪型号为API Radian Pro，其水平方向转角为640°，垂直方向转角范围为-59°～+79°，角度分辨力为0.018″，最大测量半径可达80 m，测量精度为10 μm+5 μm/m。

图9 调姿控形实验Fig.9 Experiment of pose and shape adjustment

3.1 主从协同运动实验

令6 台机器人以主从协同运动的方式分别沿主机器人基座X、Y、Z轴3 个方向运动100 mm，运动完成后使用激光跟踪仪测量相距最远主、从机器人间相对位姿偏差，重复10 次运动后取平均值，结果如表1 所示。随后，令6 台机器人以主从协同运动的方式分别绕主机器人基座的X、Y、Z轴3 个方向旋转2°，以同样的方式测量协同运动后的相对位姿偏差，结果如表2 所示。可以看出，主从协同运动中主机器人与从机器人的相对位姿偏差较小，具有较高的协同运动精度。

表1 主从协同平移运动相对位姿偏差Table 1 Error of master-slave cooperative translational movement

表2 主从协同旋转运动相对位姿偏差Table 2 Error of master-slave cooperative rotational movement

由2.3.2 节可知，主从协同运动误差与主、从机器人间的基座和法兰中心的相对位姿有关。在实际装配过程中，复合材料机身壁板产品尺寸大，主、从机器人之间的距离也会随之增加，导致主、从机器人间相对位姿误差增大，从而影响主从协同运动精度。因此，需要合理选择主机器人以减小协同运动误差。此外，实验中发现由于壁板装配调姿的运动量较小、速度较慢，主机器人轨迹规划方式对调姿过程平稳性影响较小。

3.2 位姿调整实验

壁板上架前，首先需要建立装配工装全局运动学模型。利用激光跟踪仪，测量各机器人多次相对运动后夹持单元的位姿，依据前文所述，通过各机器人多次相对运动计算未知变换关系并建立起装配工装全局运动学模型，获取未知的变换矩阵FiTCPi与WTBi。根据主从协同的原理计算出主机器人与从机器人法兰中心坐标系的变换关系FiSTFM并保存于集成控制系统中，用于后续主从协同运动控制。

待各机器人根据机身壁板外形完成预定位后，启动真空发生器，真空夹持单元完成对壁板的吸附夹持。采用激光跟踪仪测量机身壁板上设置的位姿测量点，计算出其初始位姿A0SP。将初始位姿A0SP与目标位姿TSP进行对比，若位姿偏差超过公差的容许范围，则计算主机器人的相对运动量，主机器人发送同步运动信号，各从机器人接收同步信号后，根据集成控制系统中存储的主、从机器人法兰坐标系变换关系跟随主机器人进行主从协同运动，使壁板运动到新的位姿AiSP。随后，激光跟踪仪再次测量壁板位姿。表3为3 组调姿实验结果（均为1 次调整后的结果）。

表3 调姿实验结果Table 3 Results of pose adjustment

实验结果表明，采用本文所提的主从协同控制方法进行调姿，壁板位置误差优于0.08 mm，其中X向的最大误差为0.047 mm，Y向的最大误差为0.069 mm，Z向的最大误差为0.036 mm。X、Y、Z向的方向误差优于0.008°。此外，第3 次调姿实验过程中的各机器人末端力/力矩传感器测量值（除去壁板上架后的初始值）如图10 所示。由图10 可知，主从协同运动调姿过程中壁板所受拉扯力始终保持较低水平。

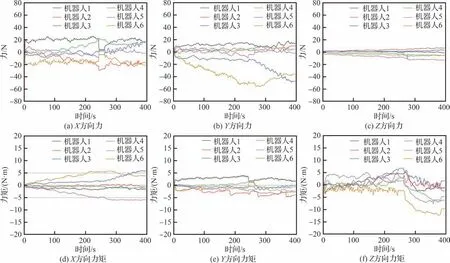
图10 机器人力/力矩传感器测量值Fig.10 Measurement data of force/torque sensors on robots

3.3 形状控制实验

为了调控复合材料机身壁板形状，满足后续机身隔框安装等工艺所需的外形精度要求，根据前文所述的形状控制方法，在壁板的内形面夹持单元区域设置形状控制点，形状控制点布局如图11 所示。

图11 形状控制点布局Fig.11 Layout of shape control points

通过激光跟踪仪测量各形状控制点，获取其实际位置，与理论数模进行对比，获取各控制点的位置偏差，并上传至集成控制系统。集成控制系统根据形状控制点的位置偏差，计算各机器人的控形运动量，并驱动机器人运动至目标位姿。待调控完成后利用激光跟踪仪再次进行测量，若偏差超差，则重复上述步骤，直至形状控制点位置偏差收敛且满足精度要求。壁板形状控制点位置偏差在调控前与调控后的数值如表4 所示。

表4 控形实验结果Table 4 Results of shape adjustment

由表4 可知，调控前SC2 与SC5 的偏差较小，而SC1、SC3、SC4 与SC6 的偏差较大。这是由于机身壁板航向截面近似为圆弧，在形状控制过程中通常以壁板水平中线为参考，调整中线两侧区域以满足外形精度要求。SC2 和SC5 位于壁板水平中线附近，SC1， SC3， SC4 与SC6 远离壁板中线，因此后者位置偏差较大。经过调控，各形状控制点偏差均减小至0.6 mm 以内，优于复合材料机身壁板装配外形偏差≤1.2 mm 的精度要求。

形状控制前后各机器人末端力/力矩传感器数值变化如表5 所示。可以看出，壁板的形状偏差越大，施加的控形力也就越大。同时，复合材料机身壁板面内刚度较大，导致较小的面内形状偏差引起了较大的控形力。此外，机身壁板为薄壁弱刚性结构件，其形状偏差主要沿面外方向，对壁板形状影响显著的机器人运动自由度为沿Z方向的平移与绕X、Y方向的旋转。但是，在机器人沿上述3 个方向驱动壁板进行形状调控过程中，不可避免地会在其余3 个方向（绕Z方向的旋转与沿X、Y方向的平移）引起壁板变形，导致调形装配力大幅增加。因此，为了在满足复合材料壁板几何精度要求的同时，最大程度地降低装配力，避免因控形力过大而导致复合材料壁板发生损伤，需对显著影响壁板外形偏差的机器人自由度采用位移控制消除形状偏差，对其余自由度采用力控模式驱动，降低外形调控过程中的装配力水平。

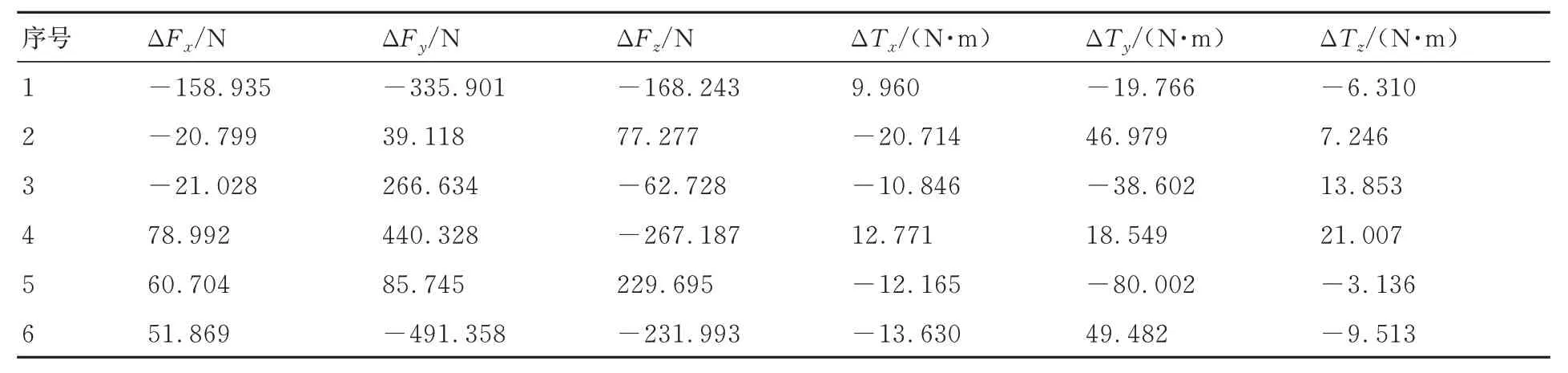
表5 机器人末端力/力矩传感器测量值变化Table 5 Variations of force/torque sensors measurement values

4 结 论

1） 根据复合材料机身壁板几何外形生成机器人夹持单元吸附夹持位置，构建了多机器人柔性装配工装系统的全局运动学模型，实现了机器人的预定位。

2） 基于主从协同运动的方法，实现了复合材料机身壁板调姿过程中多机器人的协同控制，并对主从协同运动的误差进行了分析。

3） 借助内形面形状控制点表征壁板的形状偏差，利用机器人六自由度全主动驱动的特点，通过外形面接触点位置调整使复合材料机身壁板外形达到形状精度范围内。

4） 通过复合材料机身壁板应用实验，证明了本文提出的方法具有可行性与有效性。