压气机声共振特性理论预测与试验研究

许志远，杨明绥，王萌

中国航发沈阳发动机研究所，沈阳 110015

航空发动机压气机工况复杂，导致压气机叶片疲劳失效故障的原因多样，一直都是国内外的重点研究内容。近年来，国外在压气机实际工作中发现了一种全新的导致叶片疲劳失效的声共振现象，声共振驱动源多为气动现象，如旋涡尾迹、转子-静子干涉或气流中的剪切层等。压气机发生声共振时会产生较强烈的非定常脉动，造成压气机气动不稳定性，影响结构的可靠性，甚至导致叶片疲劳断裂等故障，对发动机的整体性能特别是安全性和可靠性影响重大［1］。声共振现象类似流体诱发腔体发声问题，Rossiter［2］针对可压浅腔流动提出了声学反馈机制。上游锐缘处发生流动分离产生剪切层，剪切层在向下游运动的过程中，其扰动逐渐放大，并最终冲击到下游锐缘，冲击作用会产生较大的压力波动，并以声波的形式向上游传播。上传的声波又会在上游锐缘处形成新的扰动，完成闭环反馈。当剪切层不稳定性的时间尺度与声波从下游传到上游的时间相接近时，发生共振现象。Ma 等［3］采用先进的流场测试技术，捕捉到了气流剪切层诱发空腔发声过程中涡能与声能的发展演化现象，并指出当气流剪切层与腔体声模态发生强耦合时，会导致强烈的涡声转换现象，空腔噪声急剧增加，表现为特定频率下的噪声放大调理机制。压气机声共振现象是特指压气机内部复杂流动过程中所发生的声共振现象。针对压气机声共振问题，Parker［4-5］进行了一系列的开创性研究。Parker在风洞中进行试验时，发现在某些状态下平板或叶片振动突增，此时平板或叶片气流分离产生较强的脱落涡，脱落涡呈现频率锁定特性。通过对风洞和平板之间的声学波动方程求解，成功的计算出声共振频率和模态，声波受到机匣或相邻叶片反射后反作用于脱落涡，一旦形成正反馈循环，脱落涡便与声波频率锁定且相互增强，从而形成共振。Cumpsty 和Whitehead［6］在之后的试验中验证了Parker 提出的理论。Welsh 等［7］通过对管道内部流场的细致测量发现声共振状态下叶片尾迹出现有序的卡门涡街。Hourigan 等［8］经过计算发现，叶片尾缘脱落涡是声共振的主要声源，这一结论得到了Katasonov 等［9］试验结果的验证。Blevins［10］的试验结果表明，声波引起的声质点速度是声反馈的载体。Reyes 等［11］进一步证明，声反馈并不是作用在整个流场范围内，而主要是影响尾迹涡的脱落过程。声共振状态下出现的脱落涡频率锁定现象，正是声反馈作用的体现。Thomassin 等［12］指出转子叶片非同步振动是由叶尖涡流层在同级叶排中传播与反馈的结果导致的，叶片间产生较强的声反馈现象，表现为声能量的加剧，这种现象与Parker 声共振现象十分类似。

压气机内气动条件较为复杂，很难进行压气机内部声模态和脱落涡频率的预估，国内外在不同型号压气机试验过程中均发现类似的声共振现象。Parker［13］在某单级轴流压气机中首次发现了声共振现象，研究结果表明当压气机处于某些工况时，叶片气流分离会产生较强的脱落涡，若脱落涡频率与压气机内部某阶声模态频率接近，声场在周向形成驻波。Camp［14］在剑桥大学四级低速压气机试验器进行试验时，发现当进口导流叶片（Inlet Guide Vane，IGV）和静子叶片安装角从设计值减小10°时，会出现声共振现象。Ziada等［15］分析加拿大储气库中35 MW 多级径流压气机的声共振现象，研究结果表明声共振是由涡脱落驱动的，可通过改变支柱的后缘消除声共振。Vignau-Tuquet 和Girardeau［16］在某三级高速压气机试验台上测量到非整阶脉动压力离散频率，并且离散频率在转子转动频率和叶片通过频率（Blade Passing Frequency，BPF）之间，特征频率模态的阶数和转速都符合声共振特征。Hellmich和Seume［17］在汉诺威大学验证了四级压气机声腔共振发生在真实的环形叶栅内，声共振发生时共振频率分量的声压级已经大大超过了BPF 频率分量的声压级，压气机周向3 阶螺旋声模态在轴向表现为轴向驻波，是多级压气机的典型共振形式。国内对压气机声共振试验研究较少，杨明绥等［1］针对某型高压压气机一级转子叶片断裂故障分析叶片振动、脉动压力和噪声特征，对压气机声共振现象进行初步探索。洪志亮等［18］系统性阐述了压气机内部声共振的机理、试验测试以及预测方法等研究现状以及发展趋势，研究表明声共振源自涡声相互作用，其中声场对流场的反馈作用至关重要。

从声传播方向研究压气机声共振问题一直是压气机声共振研究的重要方法，Tyler 和Sofrin［19］提出的管道声模态理论为声模态在压气机内传播特性研究奠定理论基础。Kaji 和Okazaki［20］认为在一定条件下压气机可产生“超级共振”，叶排的传播和反射系数取决于入射波的迎角，在特定的迎角和叶片间距下，入射波和反射声场会组成一个新的声共振模态。 Kerrebrock［21］证明，对于旋流来说，漩涡、压力和熵场不再是独立的，旋流对高频脉动压力的影响很弱。也就是说，对于频率远远高于转子转速的模态来说只需要考虑声学截止的一般条件。Koch［22］基于Helmholtz 方程，预测了环形叶栅中共振声模态的频率，并探讨了叶片弦长、叶片数、叶片安装角、叶片后掠角等叶栅参数对共振频率的影响。Heinig［23］结合Koch 提出的叶片反射和传播的计算方法，提出旋流管道和叶排中声传播的计算方法。Cooper 和Peake［24］提出改变管道截面或叶排均可导致声模态发生转变，模态转变的重要原因是由旋涡起始向截止状态的转变引起的。Rienstra［25］与Ovenden 等［26］也提出了这一观点。Hellmich 和Seume［27］研究了叶排间声传播和反射特性，结果表明同级叶片间声波的模态捕获仅出现在声波波长与叶片间距尺度相当的情况。

某三级高压压气机试验件在10 150～10 900 r/min 转速范围内，叶片的一阶弯曲振动频率为755 Hz，各叶片出现“锁频锁相”特征，叶片振动频率与转速成非整阶次（4.4～4.6 不等），试验件内部出现较强的1 481 Hz 特征频率噪声，且该特征噪声伴随着一级转子叶片一阶弯曲振动出现的始末，该特征与国外压气机声共振现象十分吻合［1］。基于某三级高压压气机试验件在试验过程中一级转子叶片振动疲劳失效问题，开展高压压气机声腔共振理论预测与试验研究。

1 压气机声共振的理论预测

1.1 叶排声传播模型简化

采用Amiet［28］开发的叶排声传播模型，分析高压压气机各级叶排的声传播和反射特性，将穿过叶排的三维声场传播问题简化为二维问题进行分析求解，分析研究声学模态穿过叶片排传播特性，并进行以下假设：

1） 线性叶栅假定是无限的，不考虑边、壁对声波的反射和吸收的影响。

2） 不考虑叶片载荷。

3） 平均流动为亚声速。

4） 气流流动方向与叶栅平面平行。

5） 平面入射波角度β由模态传播角的平面展开来确定。

6） 忽略气流流动对噪声传播和反射特性的影响。

1.2 单级静子叶排声传播模型

平面声波在单级叶排中反射和传播的气动和几何参数如图1 所示。图1 中：d为叶片间距；c为叶片弦长；αs为叶片安装角；θI为入射角；θR为反射角；θT为透射角；β为平面入射波角度。

图1 声传播特性参数示意图Fig.1 Schematic diagram of acoustic propagation characteristic parameters

当声波入射方向与流动同向时，声波反射系数r和透射系数t分别由式（1）和式（2）表示。

当声波入射方向与流动反向时，声波反射系数和透射系数分别由式（3）和式（4）表示。

式（1）～式（4）中，θI为入射角；αs为叶片安装角；Ma∞为来流马赫数。L、Θ以及ψ由式（5）～式（7）确定。

参数v可通过式（8）给出。

式中：d为叶片间距；c为叶片弦长。具体参数和符号说明详见Amiet［28］开发的叶排间声传播模型。

1.3 多级叶排声传播模型

基于叶排声传播模型可以扩展得到静、动叶排反射和透射系数的计算方法。静子叶排安装角为：0 ＜αs＜90°，转子叶排安装角通常为：90°＜αs＜180°，如图2 所示。

图2 静子和转子叶排安装角示意图Fig.2 Schematic diagram of installation angle of stator blade and rotor blade row

采用Hellmich 和Seume［27］提出的方法，将转子叶排安装角沿x轴进行角度映射，映射后的安装角α's≤90°，如图3 所示，通过映射关系可实现转子叶排声传播模型的建立，具体公式为

图3 转子叶排安装角映射示意图Fig.3 Schematic diagram of installation angle mapping of rotor blade row

转子叶排声传播计算进口速度采用相对速度，静子叶排声传播计算进口速度应采用绝对速度，将绝对坐标下的转子速度与相对速度进行向量求和可实现模型从静叶系统到动叶系统的转换。基于发展的转子叶排声传播模型和静子叶排声传播模型可实现压气机多级叶排声传播模型的建立。

1.4 多级叶排螺旋声模态传播角度

在多级叶排间声传播过程中，三维螺旋声模态的传播角决定着二维简化后的平面声波入射角，因此三维螺旋声模态传播角的确定十分重要，其确定步骤如下：

步骤1传播角β为螺旋结构的倾斜角度。

步骤2在x-θ平面的传播角可由式（10）确定：

式中：kθ为周向波数；kx为轴向波数。

步骤3将三维螺旋模态展开为二维平面，模态传播角β在二维x-θ平面的示意图如图4所示。

图4 模态传播角示意图Fig.4 Schematic diagram of modal propagation angle

转子声波的传播角由式（10）确定。

式中：βabs为固定坐标系下传播角；a0为声速；r为叶片半径；N为叶片旋转速度。当声模态旋转方向与转子旋转方向相同时取负号，反之取正号。

2 声传播模型在某压气机中的应用

2.1 某压气机相关参数

某压气机发生叶片振动异常、内部噪声加剧时，根据压气机内部相关几何、气动、热力学参数获取各叶片排进口参数。压气机各级流动马赫数表达式为

式中：Max，in为进口轴向马赫数；Max，out为出口轴向马赫数。对于进口导流叶片（IGV），使用出口轴向马赫数。

弦长c的计算式为

式中：cx为叶片轴向弦长；αs为叶片安装角。

静子和转子叶片的间隔d通过式（14）确定：

式中：Rm为静子叶片中跨半径的算术平均值；πm为转子叶片中跨半径的周长；V为静子叶片数；B为转子叶片数。根据压气机各级进口参数，对压气机中跨半径处声反射和透射特性进行研究。

2.2 某压气机叶排声传播特性

某压气机静子叶排声反射和透射系数计算结果如图5 所示。由图5 可以得出，静子叶排声反射和透射特性是由入射角来确定的，当反射系数很高时，透射系数变低（如图5 中橙色区域所示）；反之，透射系数高，则反射系数变低（如图5中绿色区域所示）。在蓝色区域透射系数不为1，但在特定入射角下，反射很低，几乎接近0。在特性的角度下，入射波和反射波相互抵消，声学能量消散，在图中采用“D”进行标识，对于其他特性区域，“R”代表100%反射区，“T”代表100%透射区。

表1 一级转子应力测试结果Table 1 Dynamic stress test results of 1st rotor

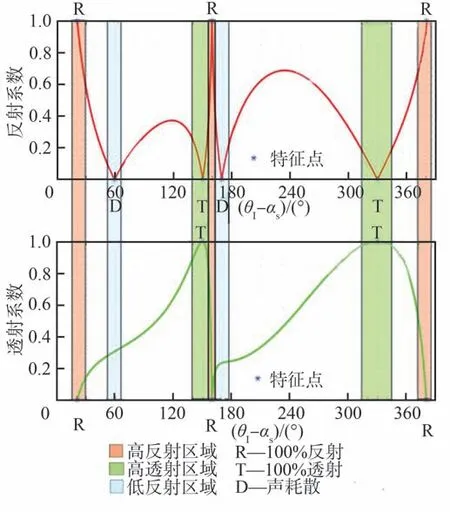
图5 某静子叶排声传播特性Fig.5 Acoustic propagation characteristics of certain stator blade row

某压气机各级静子叶排声传播特性计算结果如图6 和图7 所示，其中IGV 为进口导流叶片，S1 为一级静子，S2 为二级静子，S3 为三级静子。从图6 和图7 可以得到，压气机各级静子叶排声反射和透射特性非常类似，在高反射区（R），高透射区（T），或声波抵消区（D）入射角对声传播特性影响较大。

图6 压气机各级静子声反射特性Fig.6 Acoustic reflection characteristics of compressor stage stators

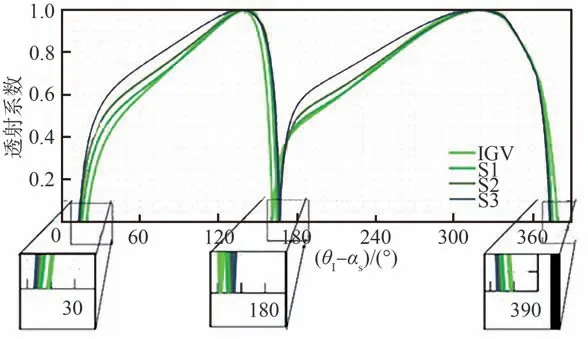
图7 压气机各级静子声透射特性Fig.7 Acoustic transmission characteristics of compressor stage stators

压气机各级转子叶排声传播计算结果如图8和图9 所示，其中R1 为一级转子，R2 为二级转子，R3 为三级转子。从图中可以得出，各转子叶排表现出类似的声反射和透射特性。同样地，入射角微小的变化，对于反射和透射特性都有较大的影响，说明各级转子声传播特性对试验件转速较为敏感。

图8 压气机各级转子声反射特性Fig.8 Acoustic reflection characteristics of compressor stage rotors

图9 压气机各级转子声透射特性Fig.9 Acoustic transmission characteristics of compressor stage rotors

3 某高压压气机声模态传播特性

3.1 特征频率声模态分析

对于轮毂比为σ的环形管道，其声模态的传播存在通过频率（Cut-On）和截至频率（Cut-Off）2 种情况。

其中对应于Cut-On 的条件为

对应于Cut-Off 的条件为

式中：f为频率；a0为声速；Ro为外径；Max为轴向马赫数；m为周向模态数；n为径向模态数；为轮毂比为σ的环形管道的特征值。现假定压气机发生声共振，则可通过Cut-On 条件计算共振频率为1 481 Hz 时压气机内部各级叶排声模态通过情况。

考虑声模态旋转方向与转子方向相同和相反两种情况，得到满足Cut-On 条件的结果如图10 所示。从图10 可以发现，噪声特征频率在IGV-R1间、S1-R2 间、S2-R3 间是截止的，而在R1-S1 间和R2-S2 间是通过的。因此可以初步判断在R1和R2 附近是引发声共振的主要部位。

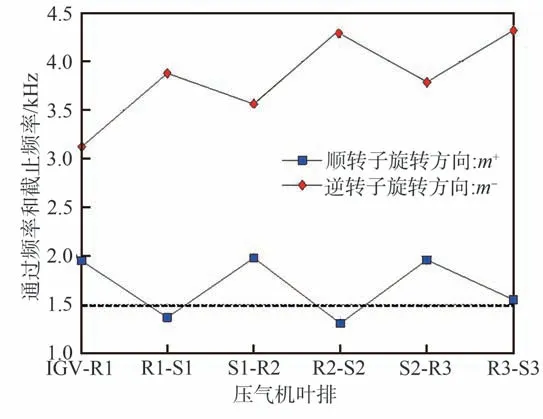
图10 特征频率下声模态传播计算Fig.10 Calculation of acoustic mode propagation at characteristic frequency

3.2 转静坐标系特征频率的理论分析

设结构模态的周向传播角速度为ω'S、声模态的周向传播角速度为ω'R、转子旋转频率为fN、声模态特征频率为fR、结构模态特征频率为fS、转子旋转角速度为ωN、声模态旋转角速度为ωR、周向声模态阶数和结构振动节径数均为m。则声模态与结构振动模态的耦合条件为

又由于

联立式（17）、式（18）可得式（19），当声模态的旋转方向与结构模态旋转方向相同时，取“负号”，声模态的旋转方向与结构模态旋转方向相反时，取“正号”。声模态与结构模态的周向耦合，将会导致在气动域和结构域中特征频率的不同。

分别将噪声频率和转子旋转频率代入式（19），改变声模态的周向模态数，计算不同周向模态数对叶片的激振频率，如图11 所示。

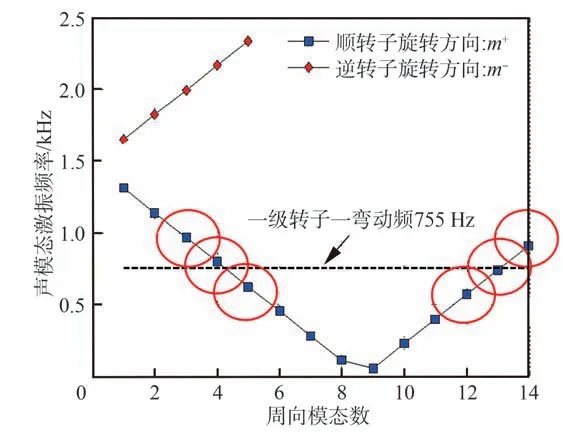
图11 声模态对叶片激振频率的计算Fig.11 Calculation of blade excitation frequency by acoustic mode

从图11 中可知，m+=3，4，5，12，13，14 这6 个模态的激振频率非常接近一级转子叶片的一阶弯曲振动频率。可以推断压气机内部声场在1 481 Hz频率下，周向阶数为m+=3，4，5，12，13，14的声模态能够激发叶片一阶弯曲振动，并且这些模态的旋转方向均与转子旋转方向相同。针对可能引起叶片一阶弯曲振动激振的声模态，进行其在叶排间声传播与反射特性的研究。

3.3 某压气机叶排声模态传播特性

压气机脱落涡与声波相互作用，形成声反馈时，脱落涡便与声波频率锁定且相互增强，从而形成共振［18］，叶排局部出现明显的声反射特性。为了检验某高压压气机中出现声共振条件，对激励模态（m+=3，4，5，12，13，14）的透射和反射特性进行研究和分析，获取压气机各级转子和静子叶排声模态在不同叶片半径下声传播特性，计算结果如图12 所示。

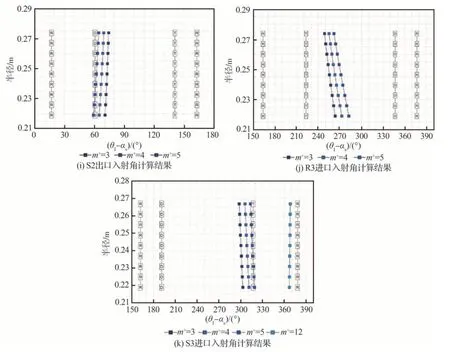
图12 压气机声模态传播特性计算Fig.12 Calculation of acoustic mode propagation characteristics of compressor

图12 中“D”为低反射、高耗散区域，“R”为高反射区域，“T”为高透射区域。计算结果表明：m+=3，4，5 的声模态在叶排间几乎完全透射，透射声波同时向下游和上游传播。对于m+=12，13，14 的声模态，声波在叶排上是反射的，并且在静子叶排上向下游传播的模态入射角，与R区域非常接近。转子叶排向上游传播的模态入射角介于T 和D 之间，反射系数在此区域局部反射系数最大，如图13 所示。

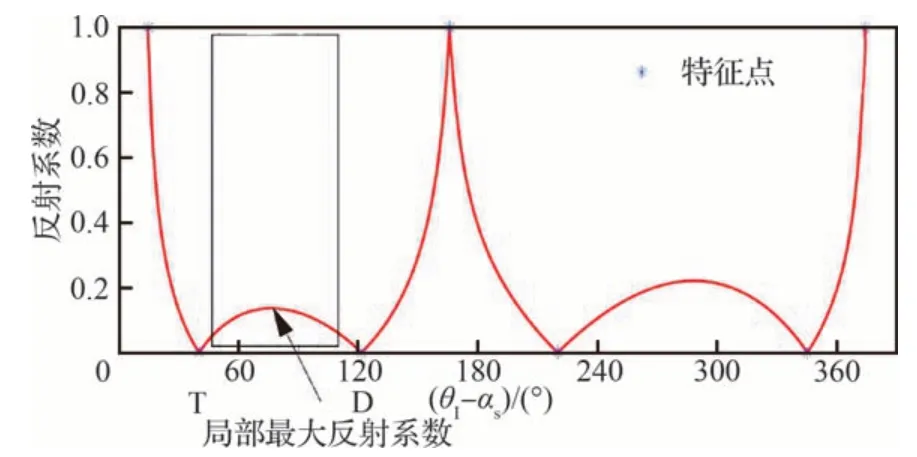
图13 R1 处声模态传播特性计算Fig.13 Calculation of acoustic mode propagation characteristics of R1

通过分析某高压压气机叶排声反射和透射特性，可以得出m+=3，4，5 的模态没有导致压气机呈现声腔共振条件，这些模态能以较低的阻抗穿过叶排进行传播。m+=12，13，14 的模态呈现出较强的声共振条件，且在转子后、静子前的位置处，体现为主要反射区。因此，基于声反射和透射条件的分析，当周向模态阶数m+=12，13，14 时，声反馈区可能形成于一、二级转子和静子间，在转子出口和静子进口处声反射系数高。根据声模态产生主反射区的入射角，得到压气机发生声共振时近似转速范围为0.85～0.92相对换算转速。

4 某压气机声共振试验研究

基于发展的声共振理论预测方法，在中国航发沈阳发动机研究所单轴双涵压气机试验器上开展某高压压气机声共振特性试验研究，对发展的预测方法进行验证。

4.1 测试方案

针对某压气机声共振现象，开展动态信号测试工作，采用脉动压传感器和应变计传感器获取压气机发生声共振时内部气动和结构振动的模态传播特性。试验件（24）次上台动态测点布置如图14 所示，在IGV 壁面布置1 个脉动压力测点，在IGV 后壁面周向均布10 个脉动压力测点，在R1 壁面沿轴向布置2 个脉动压力测点，在S1壁面布置1 个脉动压力测点，在R2 壁面布置10 个脉动压力测点，在S2 壁面布置1 个脉动压力测点，在R3 壁面布置1 个脉动压力测点，在S3壁面布置1 个脉动压力测点，共计27 点脉动压力测点。在一级转子的连续4 个叶片上布置动应变测点，测点位于一阶弯曲振动应力计算最大处。

图14 某压气机动态测点示意图Fig.14 Schematic diagram of dynamic test points of certain type of compressor

4.2 数据重复性分析

某高压压气机一级转子谐振趋于明显转速范围内，试验件沿工作线慢扫特性线如图15 所示。从图15 中可以得出，试验件在相同硬件状态不同试验次下，试验件性能重复性较好。相同换算流量下，压比偏差小＜0.3%；相同压比下，试验件流量偏差＜0.5%，满足压气机性能参数精度偏差要求。

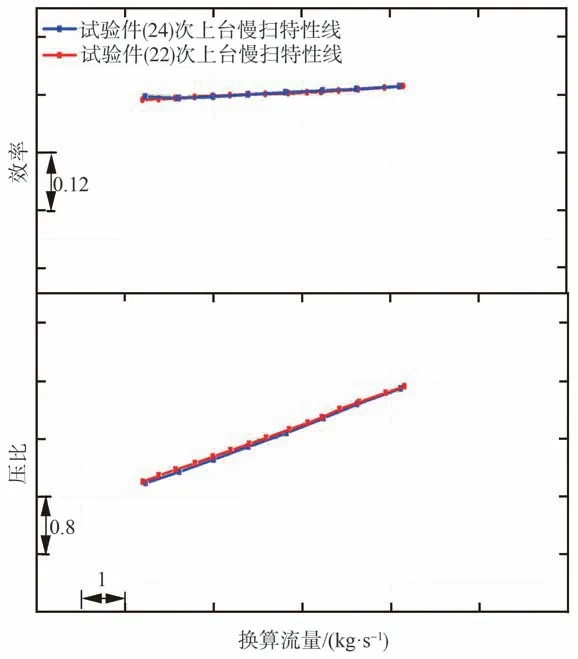
图15 某压气机慢扫描试验特性图Fig.15 Diagram of long scan test characteristics of certain type of compressor

某压气机不同试验次，相同叶片动应力测试结果如表1 所示。可以得出，试验件在叶片谐振较大转速范围内，相同转子叶片动应力测试频率和应力值相接近，叶片振动响应特性重复性较好。试验件两次上台谐振最大相对换算转速相同，物理转速存在差异，这主要是试验件进气温度不同导致的。

4.3 声共振下动态信号特征频率分析

某高压压气机试验件运转过程如图16 所示，当试验件运转至87%相对转速范围时，压气机非定常气动现象逐渐恶化，一级转子叶片谐振逐渐开始明显。当试验件转速运转至88%相对转速时，转速在10 559 r/min 附近时，压气机内部非定常脉动压力、叶片动应力均达到最大，频率为转速非整数阶次特征，压气机发生声共振转速范围与预测转速范围吻合较好。各叶片振动逐渐“锁定”为1 阶弯曲振动，频率趋于一致，动应力明显增大，符合压气机声共振特征，如图17所示。此时动应力、脉动压力的频谱如图18 和图19 所示，脉动压力和动应力频谱特征重复性较好［29］。当转速继续增加至89%相对转速时，叶片动应力、脉动压力幅值均逐渐减弱，直至现象消失。

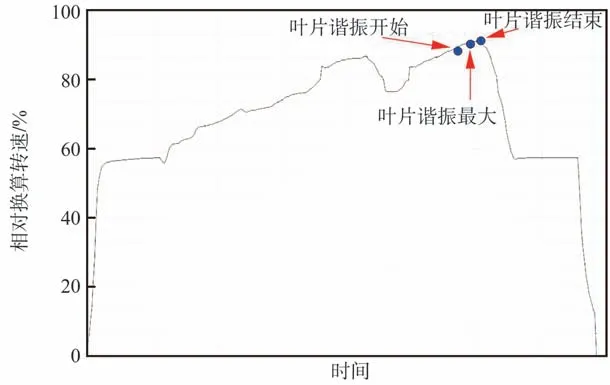
图16 某压气机试验运转情况Fig.16 Test operation of certain type of compressor

图17 叶片振动主频与转速关系Fig.17 Relation between main frequency of blade vibration and rotational speed

图18 一级转子叶片动应力频谱Fig.18 Blade dynamic stress frequency spectrum of 1st rotor

图19 一级转子上方脉动压力测点频谱Fig.19 Pressure pulse test point frequency spectrum of 1st rotor

由图18 和图19 可知，试验件转速为10 559 r/min 附近时，叶片振动体现为一阶弯曲振动，振动频率为755 Hz，为转频的4.29 倍；脉动压力与噪声的主频为1 481 Hz，为转频的8.41倍。根据转静坐标系特征频率的理论分析结果，对某压气机发生声共振时，叶片结构域与管道内气动域频率特征进行分析，可得

可以初步判断1 481 Hz 异常特征频率的+13 阶声模态可能与叶片结构模态发生周向耦合，使得气动域与结构域中存在强烈的能量交换，引起转子叶片动应力的不断加剧。试验分析得到的声模态阶次与基于声反射预测方法得到的高反射模态阶次相吻合。

4.4 声共振下脉动压力特征分析

选取试验过程中幅值最大时刻数据进行相位分析，获取幅值最大时刻周向各测点的时域信号。通过傅里叶变换获取各通道频域信号，选取参考通道，进行互谱分析，得到周向不同测点相位信息，通过相位叠加拟合得到相位拟合直线，直线斜率可近似等于模态识别结果。

4.4.1 IGV 后脉动压力模态分析

IGV 后脉动压力测点位置分布如图20 所示，共有10 个脉动压力测点，其中Z00、Z02、Z04、Z06、Z08 等5 个测点均匀分布，Z01、Z02、Z03、Z05、Z07、Z09 等6 个测点均匀分布。2 组测点共用Z02 测点，后续试验数据以该公共测点为起始点和参考零点，并参考Z09 测点进行互谱分析，得到各测点相位分析结果。

图20 IGV 后脉动压力测点分布Fig.20 Distribution of pressure pulse test points after IGV

表2 和表3 为均布脉动压力测点对Z09 做互谱后的相位分析结果。根据相位关系得到线性拟合曲线，如图21 所示，其中红线为5 点均布拟合结果，绿线为6 点均布拟合结果。拟合结果显示，IGV 后周向声模态阶次近似为13，声模态传播方向与转子旋转方向相同，与声传播模型计算结果相吻合。

表2 IGV 后脉动压力相位分析结果1Table 2 Phase analysis result 1 of pressure pulse after IGV

表3 IGV 后脉动压力相位分析结果2Table 3 Phase analysis result 2 of pressure pulse after IGV

图21 IGV 后脉动压力相位拟合曲线Fig.21 Fitted curves of pressure pulse phase analysis after IGV

4.4.2 二级转子处脉动压力模态分布

与IGV 级静子前脉动压力测点分布相类似，Z20、Z22、Z24、Z26、Z28 这5 个测点均匀分布，Z21、Z22、Z23、Z25、Z27、Z29 这6 个测点均匀分布，2 组测点共用Z22 测点，该公共测点作为数据分析的起始点和参考零点，测点分布如图22所示。

表4 和表5 为均布脉动压力测点对Z29 做互谱后的相位分析结果，根据相位关系得到线性拟合曲线，如图23 所示，其中红线为5 点均布拟合结果，绿线为6 点均布拟合结果。拟合结果显示，R2 上方周向模态阶次近似为13，传播方向与转子旋转方向相同，试验结果进一步验证声传播预测方法的准确性。

表4 R2 上方脉动压力相位分析结果1Table 4 Phase analysis result 1 of pressure pulse on R2

表5 R2 上方脉动压力相位分析结果2Table 5 Phase analysis result 2 of pressure pulse on R2

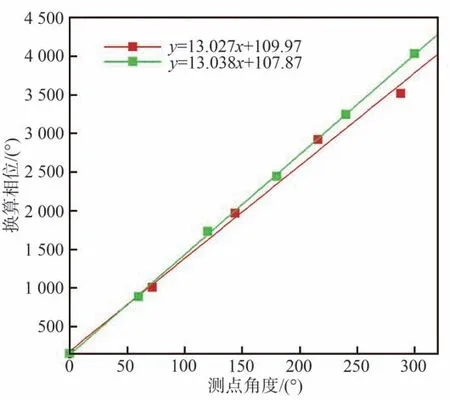
图23 R2 上脉动压力相位拟合曲线Fig.23 Fitted curves of pressure pulse phase analysis on R2

4.4.3 脉动压力轴向幅值分布

为分析压气机一级转子叶片应力异常增大时，脉动压力沿轴线方向的幅值分布规律，沿轴向位置布置9 个脉动压力测点，测点分布如图24所示。

图24 脉动压力轴向测点分布Fig.24 Axial distribution of pressure pulse test points

压气机内部脉动压力幅值轴向分布特征，如图25 所示，从图中可以得出，叶片动应力增大时，一级转子附近脉动压力幅值最大，说明一级转子附近声模态轴向传播局部反射较大，为声波主反射区，特征频率13 阶声模态在一级转子处呈现出较强的声共振条件。

图25 脉动压力幅值轴向分布Fig.25 Axial distribution of pressure pulse amplitude

4.5 声共振下叶片振动模态分析

同样，对一级转子叶片上转子4 个叶片谐振状态下的传播特性进行相位分析，相位分析结果如图26 所示。可以得到转子叶片的节径数近似为13，其传播方向与转子旋转方向相反。转子叶片的节径数与周向声模态数相同，传播方向与周向声模态相反。试验结果表明声模态与叶片结构模态存在周向耦合，在特性转速范围内，压气机内部形成声反馈，造成频率锁定，诱发压气机叶片发生声共振，引起转子叶片动应力的不断加剧，严重时造成叶片疲劳失效。

图26 R1 叶片振动的相位分析Fig.26 Phase analysis of rotor blade vibration on 1st rotor

压气机发生声共振转速范围与预测转速范围吻合较好。各叶片振动逐渐锁定为1 阶弯曲振动，呈现出锁频振动特点，符合压气机声共振特征。转子叶片振动加剧时，在内部声场、脉动压力场、同级转子叶片间均存在强烈的周向传播特性，该传播特性伴随着叶片振动加剧现象的始终。在气动域（脉动压力场）中，其周向存在约13 个行波，频率为噪声和脉动压力的特征频率，其传播方向与转子旋转方向相同。在结构域（叶片间）中，其周向存在约13 个行波，频率为转子一阶弯曲振动频率，传播方向与转子旋转方向相反，压气机轴向一级转子附近脉动压力幅值最大。这说明一级转子为声波主反射区，呈现出较强的声共振条件，试验结果与声反射预测方法相互吻合。

5 结 论

基于压气机叶排间声模态传播模型，开展某高压压气机声共振特性预测与试验研究，主要结论如下：

1）发展压气机声共振特性理论预测方法，预测结果表明某压气机特征频率下m+=12，13，14 的声模态在转子和静子间传播时，局部反射系数较高，呈现出较强的声共振条件。

2）某压气机发生声共振转速范围与预测转速范围吻合较好，发生声共振时各叶片振动逐渐锁定为一阶弯曲振动，频率趋于一致，符合压气机声共振特征。

3）转子叶片振动加剧时，压气机内脉动压力场、同级转子叶片间均存在强烈的周向传播特性，周向传播模态为13 阶，且存在关系：转子叶片一弯振动频率阶次+脉动压力特征频率阶次＝周向声模态传播阶次，声模态与叶片结构模态存在周向耦合。压气机轴向级转子附近脉动压力幅值最大，说明一级转子附近局部反射较大，为声波主反射区，特征频率13 阶声模态在一级转子处呈现出较强的声共振条件。与预测结果相吻合。

计划下一步开展模型试验器声共振理论和试验研究，在模型试验器上研究试验件发生声共振时声模态传播特性和叶片振动特性，并发展压气机声共振抑制方法。