六年级数学期末综合评价

○泊头市教师发展中心 王俊华

一、认真思考，正确填写

1.嫦娥四号和嫦娥五号探测器对于材料的要求极高，因为月球表面的昼夜温差约310摄氏度，白天在阳光垂直照射的地方温度高达+127摄氏度，夜晚最低可降到（）摄氏度。

2.9÷12=（）∶4=（）×0.25=（）%。

3.京张高速铁路是2022年北京冬奥会的重要交通保障设施之一,全长174千米,其中北京境内长a千米,剩余都在河北境内。如果高铁以每小时350千米的速度行驶,在河北境内需要开()小时。

4.根据算式填条件。

育才小学六年级有男生240人，_________，女生有多少人？

（1）240÷30%条件:（）。

（2）240×(1+20%)条件:（）。

6.把一个棱长为6厘米的正方体木块削成一个最大的圆柱，圆柱的体积是（)立方厘米，再把这个圆柱削成一个最大的圆锥，这个圆锥的体积是（）立方厘米。

7.商店对某种饮料推出“第二杯半价”的促销活动，买2杯这种饮料相当于在原价的基础上打了（）折。

8.按照“四舍五入”法，近似数为5.00的最大三位小数是（），最小三位小数是（）。

9.如果a+1=b（a、b均为非0自然数），那么a和b的最大公因数是（），最小公倍数是（）。

10.Δ○○☆Δ○○☆Δ○○☆……

左起第50个是（）；前50个图形中，○有（）个。

11.下面表格中，如果x和y成正比例关系，“？”处填（）；如果x和y成反比例关系，“？”处填（）。

x y 5？20 16

12.去掉1.258的小数点，把它变成整数，增加了原数的（）倍。在68.5的后面添上“%”，减少了原数的（）%。

13.把35个苹果最多放到（）个盘子里，可以保证总有一个盘子里至少有9个苹果。

14.一个车间改革后，人员减少了25%，产量比原来增加了20%，则工作效率提高了（）。

15.□、○、Δ各代表一个数，已知：□－○=24，□＋○=30，Δ=□+□+○，则□=（），○=（），Δ=（）。

16.一个圆柱,如果把它的高截短3厘米（如图①），表面积就减少94.2平方厘米，这个圆柱的底面半径是（）厘米；如果把原来这个圆柱的底面平均分成16份后切开拼成一个近似的长方体（如图②），表面积就比原来增加100平方厘米，那么这个圆柱的体积是（）立方厘米。

①

②

二、仔细分析，正确判断

（）1.假分数的倒数一定是真分数。

（）2.一个数不是正数就是负数。

（）3.如果一个三角形中的两个内角之和小于90度，那么这个三角形一定是钝角三角形。

（）4.圆柱的侧面展开图一定是长方形或正方形。

（）5.在a÷b=4……3中，把a、b同时扩大10倍，商和余数都不变。

（）6.一本少儿读物的价格先降价5%，又降价15%，现价是原价的80%。

（）7.等底等高的圆柱、正方体、长方体的体积一样大。

（）10.某商场推出促销活动“满500元减50元”，因为(500-50)÷500=90%，所以“满500元减50元”就是打九折销售。

三、反复推敲，正确选择

1.探究圆柱的体积依次经历了（）的过程。

A.推导公式、转化图形、寻找关系

B.转化图形、寻找关系、推导公式

C.转化图形、推导公式、寻找关系

D.寻找关系、转化图形、推导公式

2.下面各数量关系中，成正比例关系的是（）。

A.长方形的宽一定，它的长和周长

B.儿童的年龄和体重

C.圆柱形水桶的底面积一定，水的高度和水的体积

D.被除数一定，除数和商

3.下面图形的变化过程，可以用算式（）表示。

A.8∶21 B.3∶14

C.14∶3 D.21∶8

5.下面各组中的两个比，能组成比例的是（）。

6.如图所示，一个密闭的容器是由圆柱和圆锥组成的，圆柱和圆锥的高分别为12厘米、9厘米，容器内的液面高8厘米。如果将这个容器倒过来放，从圆锥的顶点到液面的距离是（）厘米。

A.8 B.5

C.14 D.11

7.一个长26厘米、宽19厘米、高0.7厘米的物体，最有可能是（）。

A.书橱B.手机

C.数学课本D.课桌

8.甲、乙、丙三个小朋友用相同的正方形手工纸剪圆。如图所示，甲剪了一个最大的扇形，乙剪了四个相同的圆，丙剪了一个最大的圆，则()。

A.甲剩下的手工纸多

B.乙剩下的手工纸多

C.丙剩下的手工纸多

D.甲、乙、丙剩下的手工纸同样多

9.走完同一段路，甲用8分钟，乙用9分钟，甲和乙的速度比是（）。

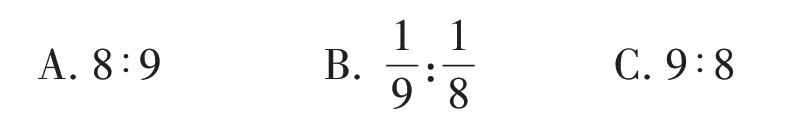
A.x＞y＞zB.x＜y＜z

C.x＜z＜yD.y＜z＜x

11.一个圆柱和一个圆锥等底等高，如果圆锥的高增加24厘米，则圆锥和圆柱体积相等，那么圆柱的高是（）厘米。

A.6 B.9

C.3 D.12

12.有大、小两种纸杯与甲、乙两桶果汁，小纸杯与大纸杯的容量比为2∶3，甲桶果汁与乙桶果汁的体积比是3∶5。若甲桶内的果汁刚好装满135个小纸杯，则乙桶内的果汁最多可装满()个大纸杯。

A.180 B.100 C.150

四、细心计算，不出差错

1.直接写得数。

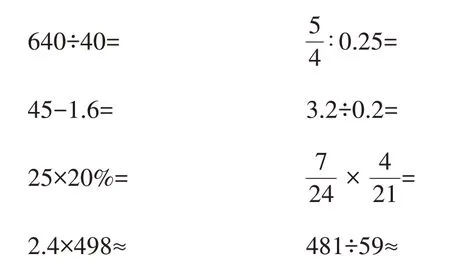
2.计算下面各题，怎样简便就怎样算。

3.求未知数x。

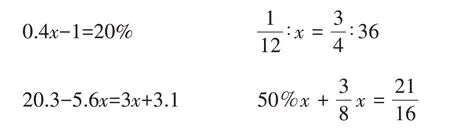
4.求下面立体图形的表面积和体积。（π取3.14）（单位：厘米）

五、动手操作，探究实践

1.求旋转所成图形的体积。（π取3.14）

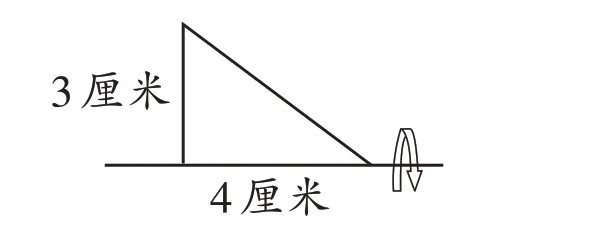
2.（1）画出三角形A B C绕点C按顺时针方向旋转90°后的图形，旋转后点B对应点的位置用数对表示为（，）。

（2）画出三角形ABC按2∶1扩大后的三角形A1B1C1，三角形A1B1C1的面积是三角形ABC面积的（）倍。

六、走进生活，解决问题

1.学校要买一些笔记本，每本3.5元，甲商场打八折，乙商场“买八送二”，丙商场“每满100元返25元现金”，学校想买300本，到哪家购买最划算？

2.一根木棍，锯成7段需要15分钟；照这样计算，如果锯成11段，需要多少分钟？

3.学校用的自来水管内直径为0.2分米，自来水的流速为每秒5分米。如果你忘记关上水龙头，一分钟将浪费多少升水？

4.为了鼓励节约用电，某市电力公司规定了以下电费计算方法：每月用电不超过180度时，按每度0.55元收费；每月用电超过180度时，超过部分按每度0.60元收费。7月聪聪家付电费127.8元，他家用了多少度电？

5.水果店进了某种水果1000千克，进价为7元/千克，售价为11元/千克，售出一半后，为了尽快售完，准备打折出售，要使这批水果能赚到3450元，余下的水果应按原售价打几折出售？

6.甲、乙两地相距300千米，李叔叔从甲地到乙地，每小时行75千米，返回时每小时行50千米，往返一趟平均每小时行多少千米？

7.根据图中给出的数量关系编一道数学问题，不用解答。

8.甲、乙两列火车同时从A地向相反方向行驶，分别驶往B地和C地，已知A、B之间的路程是A、C之间路程的。当甲车行驶60千米时,乙车行驶的路程与剩下路程的比是1∶3，这时两列火车离目的地路程相等。求A、C之间的路程。

9.近三年来,新型冠状病毒成为人们关注的焦点。为了调查学生对预防知识的了解程度,某校在学生中做了一次抽样调查,调査结果共分为四个等级：A非常了解；B.比较了解；C.基本了解；D.不了解。根据调查统计结果，绘制了不完整的三种统计图（表）。

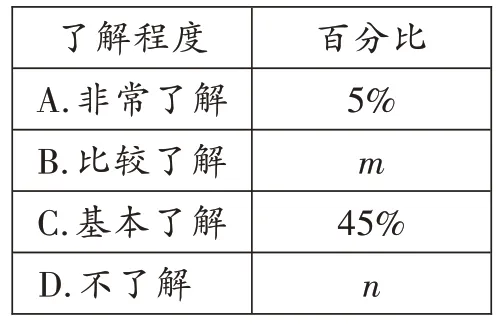
对预防知识了解程度统计表

对预防知识了解程度扇形统计图

对预防知识了解程度条形统计图

请结合统计图(表),回答下列问题。

（1）表格中m=_____，n=_____。

（2）扇形统计图中，D部分扇形所对应的圆心角应是_____度。

（3）请补全条形统计图。