液压支架双伸缩立柱在冲击载荷下的受力仿真研究

梁凯杰

（霍州煤电集团鑫钜煤机装备制造有限责任公司， 山西 霍州 031400）

0 引言

双伸缩立柱作为液压支架中的核心部件，可以确保支架具有支撑稳定性，结合冲击载荷对支架的影响，一般要远高于静载荷，具体会出现立柱胀缸和变形的问题，严重时还会导致立柱爆裂，因此有必要了解冲击载荷下液压支架立柱的受载特性。为了提高研究的有效性，基于弹簧串联原理先了解双伸缩立柱的刚度公式，进而得到立柱液压缸内的压力公式，同时需要将重锤冲击立柱的动态加载转变为缸内的液压静态加载，最后借助Workbench 软件进行双伸缩立柱的仿真，研究冲击速度和不同乳化液液柱高度与立柱一、二级缸最大应力变化的关系。

1 液压支架立柱的受力

1.1 等效刚度理论

借助重锤冲击立柱模拟真实场景中冲击载荷对双伸缩立柱的影响，基于重锤质量明显高于立柱活柱的质量，因此在冲击瞬间可以将立柱看为一个具有等效刚度K 的轴向弹性元件（二级缸弹簧体和一级缸弹簧体视为串联）。同时将立柱缸内乳化液与缸体分别看作液体等效弹簧与固体等效弹簧，因此单个液压缸等效刚度就为以上两者的串联，且整体立柱的等效刚度则为1、2 级缸的串联。

下面将基于体积弹性模量进行第i（i=1、2）级缸的等效刚度分析：

第i 级缸液体的等效刚度可以参考式（1）：

式中：Ai为第i 级缸的内径圆面积，m2；di为第i 级缸的内径，m；hi为第i 级缸的内液柱高，m；Ky为5%的乳化液体积弹性模量，取1.82 GPa。

第i 级缸固体的等效刚度可以参考式（2）：

式中：Kg为缸体体积模量，Pa；E 为缸体弹性模量，GPa；μ 为缸体泊松比。

由式（1）、式（2）可得第i 级缸的等效刚度，具体参考式（3）：

基于式（3）可以得出缸内液柱高度和其等效刚度成负相关的结果，且借助等效刚度理论，可以确定液压支架立柱的等效刚度K，参考式（4）：

1.2 缸内压力公式

以ZY8640/2550/5500 型掩护式液压支架的立柱为例，支架的初撑压力为42.3 MPa，为了满足试验中的冲击条件，需要拟定重锤的质量m 为28 000 kg，且接触速度定为3 m/s。其中冲击载荷下的双伸缩立柱的一、二级缸最大压力Pi计算可以参考式（5）：

式中：ymax为冲击震动的最大位移，m；p0为支架初撑压力，Pa；m3为活柱质量，kg；g 为重力加速度，m/s2。

基于以上式（1）—式（5）可以计算得到一、二级缸的最大压力，分别为91 MPa、173 MPa[1]。

2 立柱受力的有限元仿真分析

2.1 仿真试验

利用SolidWorks 软件建模。要先了解立柱的结构并进行一定简化，使立柱成为整体模型，具体在简化后，立柱的结构主要包括一级缸、二级缸、导向套和活柱；将SolidWorks 软件中的建模文件导入Workbench中，并进行网格划分。同时关注导向套材料和立柱缸体材料的选择，具体使用27SiMn 高强度钢，在材料参数上有以下几点：弹性模量为205 GPa、泊松比为0.3、密度为7 840 kg/m3、抗拉强度为980 MPa、屈服强度为836 MPa，在做好选择后从Workbench 材料库中添加；结合以上基于重锤冲击所计算的一、二级缸最大压力，可以将其视为立柱液压缸内乳化液压力作用，进而再分别施加一级缸、二级缸91 MPa、173 MPa 后，确保立柱液压缸内的压力达到最大化，然后进行仿真试验，得到具体的应力和变形云图。其中一级缸和二级缸的应力云图见图1。

图1 一、二级缸的应力云图

2.2 仿真数据

结合立柱的整体应力和整体变形云图看，立柱的整体应力和变形都较小；结合二级缸应力和变形云图看，二级缸在缸壁整体部分存在应力较大的现象，且最大应力与最大变形都在二级缸内靠近活柱活塞的地方，具体最大应力数值为685 MPa，较为接近27SiMn 材料的屈服极限值，可在缸底进行加厚处理；结合一级缸应力分布而言，最大的应力出现在缸底处，具体为620 MPa，整体较为安全；结合一、二级缸变形云图而言，变形量都有着从上到下逐渐递减的特点，且二级缸的最大变形量远大于一级缸的最大变形量；结合大、小导向套应力云图而言，大、小导向套的最大应力点分别位于导向套顶端和导向套底端，且两者最大应力值均低于对应材料的屈服强度，整体也较为安全[2]。

3 立柱仿真结果讨论

3.1 不同冲击速度

在保持重锤质量不变仅改动重锤的冲击速度时，结合式（5）可以计算出缸内压力数值，然后在立柱的仿真试验中分别施加不同的压力数值并确保其余边界条件无变化，最后可以得到立柱一、二级缸的最大应力数值，基于重锤冲击速度的改变，对应立柱一、二级缸的最大应力也会改变，具体见图2。结合图2，重锤对一、二级缸最大压力的影响与冲击速度的提高相关，且呈现正相关。具体在以4 m/s 的速度进行冲击立柱时，二级缸的最大应力为820 MPa，与27SiMn 高钢材料的屈服极限836 MPa 较为接近，需要在液压支架的选型上参考实际工况，降低设备损坏概率[3]。

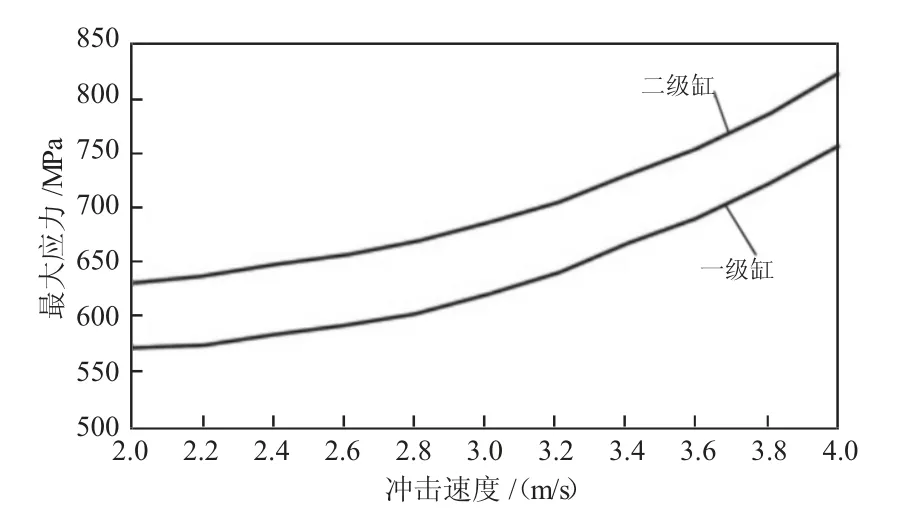
图2 重锤冲击速度对立柱液压缸最大应力的影响

3.2 缸内不同液柱高度

在确保重锤质量（28 000 kg）和冲击速度（3 m/s）无变化下，基于立柱液压缸内乳化液高度对立柱最大应力的影响，可以取变量为完全伸出长度50%～100%的乳化液液柱高度，结合式（5）可以分别得到液压缸内的压力值，在导入立柱的仿真试验并确保其余边界条件不变下，可以得到立柱一、二级缸的最大应力，具体见图3。以图3 所显示的液柱高度与最大应力的关系，随着液柱高度的提高，对应冲击载荷产生的作用力越小，立柱的应力会不断降低，本质上是因为液柱高度的提高会降低立柱的整体刚度，使乳化液更具有良好的缓冲作用。对于二级缸而言，当液柱高度为立柱完全伸出时液柱高度的60%时，最大应力值为830 MPa，与27SiMn 高钢材料的屈服极限基本相同，且在液柱高度在50%～60%时，二级缸的最大应力值已超过27SiMn 高钢的强度极限，会出现胀缸等故障。

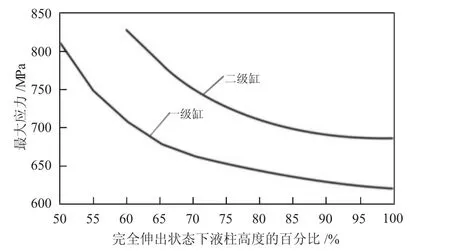
图3 液柱高度对立柱液压缸最大应力的影响

4 结语

结合固液耦合和弹簧串联理论可以了解到立柱液压缸的等效刚度，进而能得出基于重锤冲击下立柱液压缸内乳化液的最大液体压力。在为仿真试验奠定基础后，经过实际的仿真分析可以发现立柱二级缸的受力大于一级缸，且实际应力接近材料的屈服强度，基于二级缸的最大受力点位于靠近活塞处，需要在立柱结构设计中考虑增大二级缸的壁厚，避免应力过大出现胀缸。最后，结合冲击速度和液压缸内乳化液含量对缸内最大应力的影响，可以在有效分析后为更加真实的立柱冲击试验提供参考，最终满足煤矿企业井下生产的安全性需要。