论旋转思想在初中数学解题中的妙用
林艳娜
(福建省福州英才中学,福建 福州 350026)
在初中数学解题教学中,教师需指引学生结合具体题目巧妙应用旋转思想,使其尽快找到解题的切入点,简化解题过程,使学生高效解答试题.
1 合理运用旋转思想,解决线段长度问题
教师在平常的解题教学中应当指引学生合理运用旋转思想,对题目中的图形进行旋转和变形,使其明确旋转后的变化情况,让他们快速确定解题方案,解决线段长度问题[1].
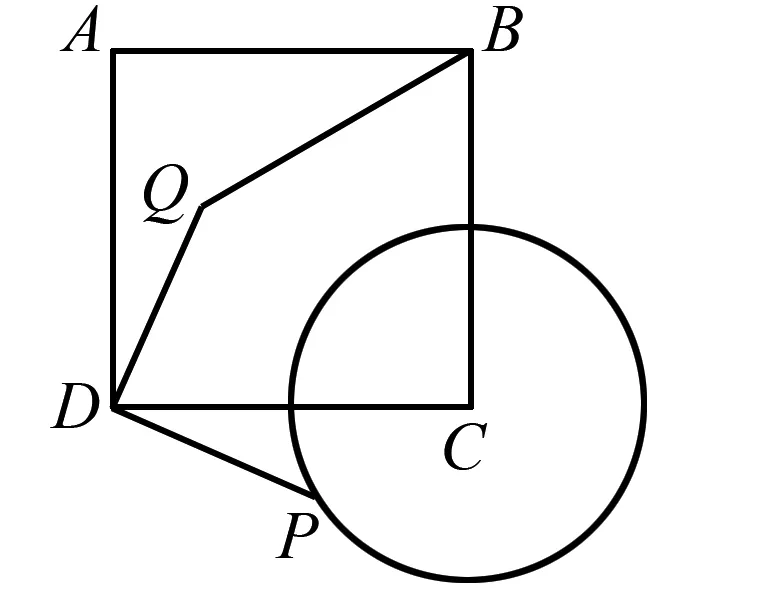
例1如图1所示,在四边形ABCD中,AD∥BC,AD 图1 例1题图 分析利用旋转思想,把△BCE围绕点B进行顺时针旋转90°,刚好可以得到一个正方形,如图2所示,然后根据三角形全等的性质找到边与边之间的关系,即可求出CE的长度. 图2 例1题图 解将△BCE围绕点B顺时针旋转90°得到△BGM,这两个直角三角形是全等关系,C、E两点分别旋转至G、M点处,BC、CE、BE分别旋转至BG、GM、BM,∠CBG=∠BGD=90°,由此得到正方形BCDG,∠ABE=∠ABM=45°,△ABE≌△ABM,那么AM=AE=10,设CE是x,则有AG=10-x,AD=12-(10-x)=2+x,DE=12-x在直角三角形ADE中,AE2=AD2+DE2,代入相关数据后得到102=(2+x)2+(12-x)2,解之得x1=4,x2=6,故CE的长度是4或6. 通过对初中数学计算线段最值类问题的研究与梳理,发现利用旋转思想往往能够起到意想不到的效果,学生运用旋转思想以后找到点的特殊位置,根据图形形式与勾股定理进行求解,让他们顺利解决线段最值问题[2]. 例2如图3所示,以边长是4的正方形ABCD的C点为圆心,半径是2画圆,点P是圆C上面的任意一点,让点P围绕点D逆时针旋转90°得到点Q,把BQ连接起来,那么BQ的最大值是什么? 图3 例2题图 分析在本题中,线段围绕一个点进行逆时针旋转90°,根据图形可知∠CDP=∠ADQ,可得出△AQD≌△CPD,把CP与AQ连接起来,可得AQ的长是定值2,点Q的轨迹是一个圆,即可求出BQ的最大值. 解将CP与AQ连接起来,根据旋转可知∠QDP=∠QDC+∠CDP=90°,根据正方形的性质可得AD=DC,∠ADQ+∠QDC=90°,则∠CDP=∠ADQ,△AQD≌△CPD,AQ=CP=2,点P在圆C上运动时,Q点也会随之运动,不过AQ保持2的定值始终不变,据此可知点Q的运动轨迹是以点A为圆心的圆,当BQ有最大值时,点Q、A、B共线,且点A位于点B与Q之间,这时BQ=AB+AQ=4+2=6. 处理一些涉及图形旋转类的初中数学题目时,教师可引导学生利用旋转思想,找到旋转前后图形线段、角度之间的内在联系,以此确定解题思路,从而求出线段比值[3]. 例3 如图4所示,四边形ABCD是一个边长为2的菱形,已知一个内角是72°,该菱形围绕点D旋转得到菱形A′B′C′D′,AB与B′C′相交于点P,把BB′连接起来,当五边形A′B′BCD′是正五边形时,求BP:AP的值. 图4 例3题图 分析因为旋转以后得到的是一个正五边形,可知内角是108°,旋转后线段长度与首尾顺序均不发生变化,结合菱形、等腰三角形以及相似三角形的性质进行解题. 针对角度计算类试题,初中数学教师应指导学生巧用旋转思想,通过对原图形的旋转与变化把一些条件整合到一起,分析图形的特殊角度及位置,使学生结合有关公式进行计算,从而把复杂、陌生的问题变得简单与熟悉[4]. 例4 如图5所示,点P是等边三角形ABC内的一点,已知PA=3,PB=4,PC=5,求∠APB的值. 图5 例4题图 分析当学生看到题目中出现3、4、5的数据时,很容易想到勾股定理,是同一个直角三角形的三条边,但是在本题中并没有位于同一个直角三角形内,此时他们可想到应用旋转思想,把这三条边集中到同一个直角三角形里面. 解先让△APB围绕点A按照逆时针方向旋转60°后得到△ADC,连接PD,如图6所示,则有AD=PA=3,DC=PB=4,∠PAD=60°,得到一个等边三角形PAD,则PD=PA=3,∠ADP=60°,在△PDC中有PD2+DC2=PC2,这表明△PDC是一个直角三角形,且∠PDC=90°,由此得到∠APB=∠ADP+∠PDC=60°+90°=150°. 图6 例4题图 在初中数学解题训练中,求解图形面积类的试题离不开旋转思想的辅助与支持,可以把零散的图形集中起来.处理这类试题的关键在于确定好旋转对象与角度,教师在平常的解题训练中需加强指导,让学生准确把握旋转对象和角度,帮助他们轻松解决面积计算问题[5]. 图7 例5题图 分析本题可使用旋转思想,将△AED围绕点A顺时针旋转90°,然后把两个三角形拼接起来,根据题意能够判定出拼接的三角形又由两个直角三角形构成,结合正方形的性质用勾股定理等即可完成解题. 图8 例5题图 旋转思想在初中数学解题中可谓是有着极为广泛的应用空间,是一种极为重要与常用的数学思想方法,教师应围绕旋转思想专门开设习题训练活动,指导学生学会如何妙用旋转思想解决数学问题,使其充分感受到旋转思想在解题中的妙用,继而提高他们的解题水平[6].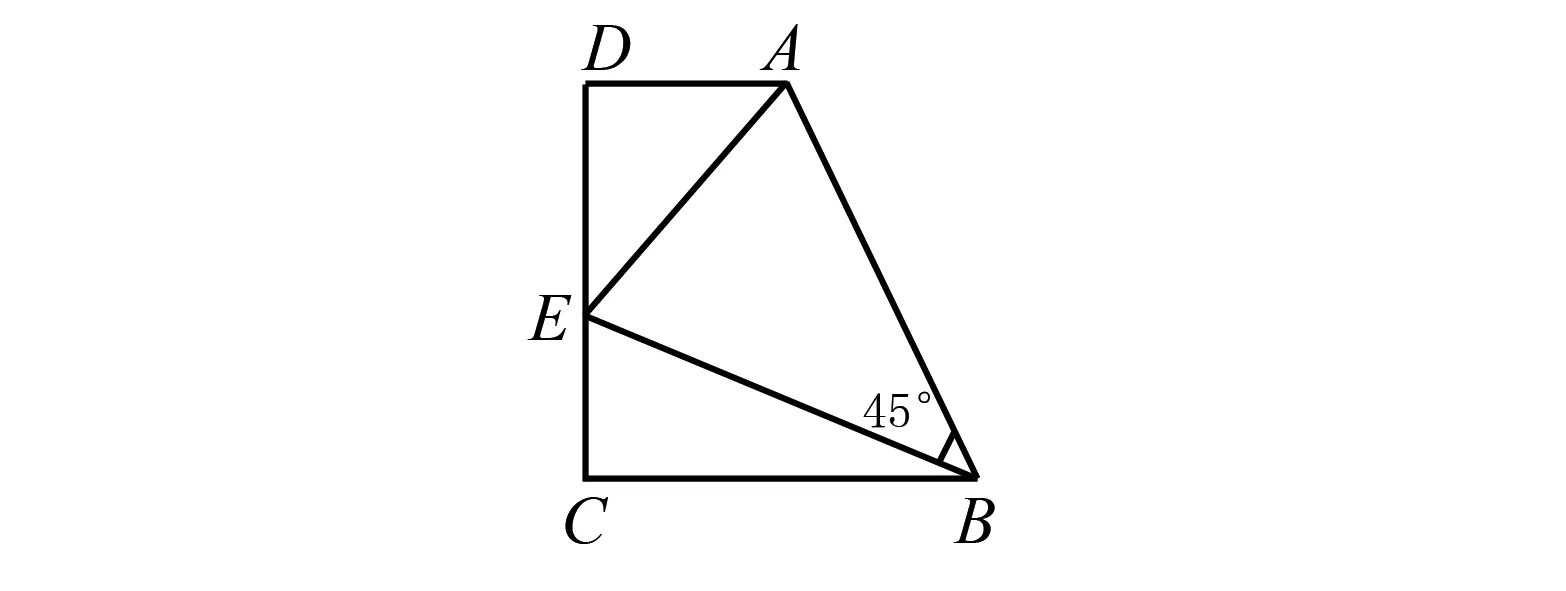

2 利用旋转思想,解决线段最值问题
3 利用旋转思想,解决线段比值问题

4 利用旋转思想,解决角度计算问题


5 利用旋转思想,解决面积计算问题





