基于Grasshopper的传统悬山顶参数化设计研究

孙 皓, 邓先农, 赵若桐

(湖北工业大学土木建筑与环境学院,湖北 武汉 430068)

中国古代木构建筑的构成有严密的生成逻辑,《营造法式》中有“凡构屋之制,皆以材为祖;材有八等,度屋之大小,因而用之[1]。”通过开间和进深以及材料模数等参数就能确定整个建筑的形体,这样不仅能使建筑在建造初期可以得到控制,同时也能精确地对用材量进行计算。参数化设计(Parametric Design)也称参变量化设计,即设计过程被参变量化,利用参变量来控制模型的生成和性质[2]。中国古建筑的模数化思维以及生成逻辑十分适合计算机参数化设计,因此可以利用参数化建模对古建筑进行复原,从而实现快速建模。

对于古建筑参数化相关研究,目前国内外主要集中于分析古建筑的各个构件从而建立参数化构件数据库。熊芳芳利用VC#.NET开发界面,基于数据库对北京四合院进行参数化建模,实现了参数化构件数据库读取和归档[3]。王茹通过研究古建筑形制化集成的特点,提出了以斗口模数十一等材为基础模数,建立了一个古建筑常用3D构件库,同时也开发了对应的可视化接口,为快速搭建古建筑模型奠定了基础[4]。闫泽文提出了正向建立古建筑典型构件模型的方法,利用Revit平台,以单翘单昂平身科斗拱为例,创建了该构件的三维BIM模型,为构建古建筑构件BIM族库做出了贡献[5]。孙卫新研究了明清古建筑的组成和构成方式,并对主要建筑构件进行了参数化建模研究,最终建立了完整的三维模型[6]。

综上可见,目前大多研究主要集中于古建筑参数化构件的研究,没有考虑其整体性,不考虑整体性的模型容易出现模型冲突等问题,本文从整体性考虑,通过研究古建筑的构造,以传统悬山顶建筑为例,利用参数化工具建立参数化模型。

1 参数化建模技术

传统建模技术称之为模拟建模技术(Analogical Modeling),即每次修改模型都要对模型的几何元素(点、线、面等)进行直接操作。这个技术操作方便,所见即所得,但是最大的缺点在于几何元素相互独立存在,导致了对其中一个对象或参数进行修改不会对其他对象产生影响,如果想对其反复修改则十分浪费时间。其次,对于完成度很高的模型,若再次进行较大的修改则十分费时费力,甚至等同于重新制作模型。

参数化设计是一种计算机辅助设计技术,它基于拓扑学思想,拓扑学(topology)是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科。拓扑思想起源于几何学,最开始参数化设计用来解决对象的几何形式问题,但是随着技术发展,现在也可以用来解决一些非几何问题。比如研究建筑功能与开窗形式的问题,若想改变建筑的功能,只需改变对应参数,其他被绑定的参数也会自动进行调整,从而改变开窗的形式。参数化设计的出现使得建筑设计行业可以真正专注于设计本身,通过调整参数,计算机可以实时反馈设计的结果,而不用花费大量时间重绘图纸,从而将更多的精力放在推敲设计上。

参数化模型又称为“关联模型”(Associative Model),即模型之间由参数驱动产生关联,从而实现联动。参数化建模技术相比于模拟建模技术在某些方面更有优势。首先,参数化模型利用数值参数来控制几何元素,只需输入对应的命令和参数就能对模型进行调整,模型越复杂,调整效率优势越明显。其次,参数化模型的位置约束也可参数化,将一个模型与其他模型利用参数进行关联后,当变动初始模型的参数时,其他的关联模型也随之变化,修改的效率得到极大提升[7]。

2 悬山顶参数化建模

2.1 悬山顶构造分析

悬山顶是中国古代建筑的一种屋顶样式,其特点是悬山建筑两山的檩头伸出山墙之外,伸出山墙的檩用于支撑悬挑的屋面部分。因悬山顶建筑的前后檐和两端都有悬挑部分,而得名悬山顶,图1为悬山顶建筑。

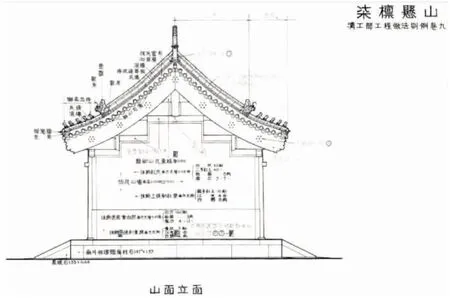
图1 悬山顶建筑

根据悬山顶的特点,建模思路可以自上而下来进行生成,也就是屋面-梁-柱的顺序。依照这个顺序,大体将建筑分为上下两部分来进行制作,上层为屋面,下层包括梁和柱。

2.2 建模分析

本文选用Grasshopper作为参数化建模平台,设计思路是根据规则和尺寸要求确定每个构件的点位形成定位点模型,利用这些点位可以进行各种命令生成线或面或体块。首先确定模型由哪些基本参数控制,再与其他构件的尺寸建立函数关系,从而实现联动。经考虑,将以下尺寸参数作为基本参数:面阔K、进深S、椽子半径r。确定了基本参数后,其他的构件尺寸均可以根据基本参数和一定的比例系数推算出来。先赋予三个基本参数初始值K=4.5 m、S=1.5 m、r=0.1 m。

首先确定平面定位点,考虑建筑为对称结构,又因举折生成逻辑需要,故在进深方向设置6个点位,以第六个点的连线所在的XZ平面为对称平面,面阔方向设置为8个点位为七开间,点位如图2所示。则建筑进深长度为5S,面阔总长度为7K。

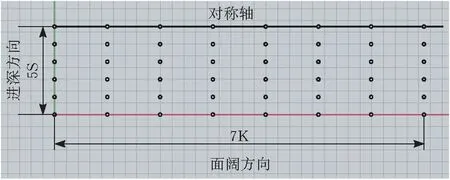
图2 平面定位点图

2.3 算法生成模型

确定控制点后,先从上层开始建模,上层建模难度主要在于举折生成。举折是中国古代建筑确定屋顶曲面曲度的方法,举是指屋架的高度,称为举高(R),其大小根据建筑的总进深(B)和屋面材料来确定,建筑总进深为前后橑檐坊心之间的水平距离,在宋式建筑中,通常举高与总进深之比为1/4～1/3,为了计算方便,本文取1/3。折是指屋面横断面坡度由若干折线组成,这是因为建造屋架时,各檩升高的幅度不一致,所以坡度并非一条直线,如图3所示。

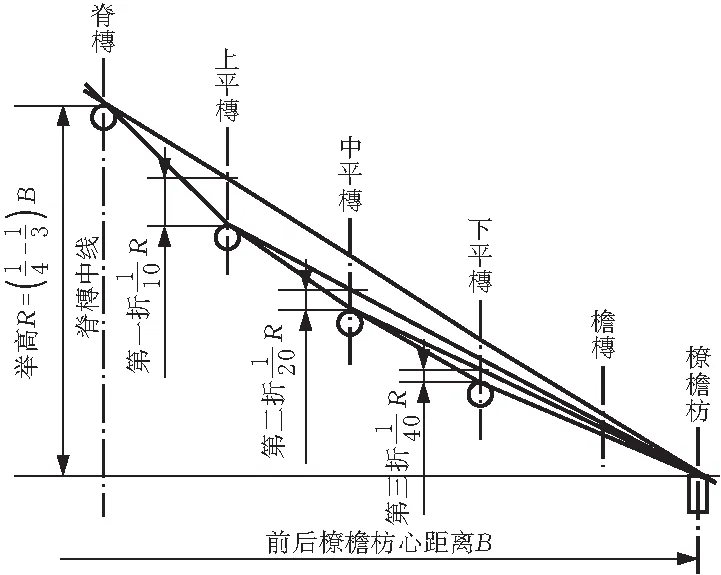
图3 举折设计图

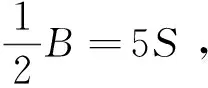
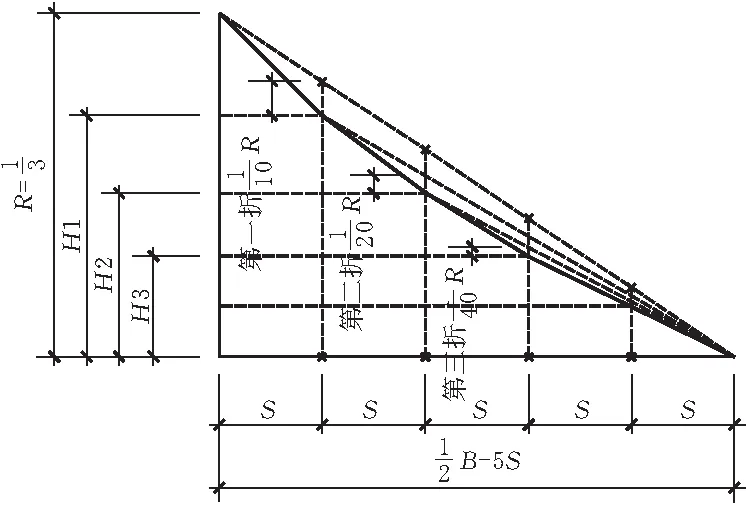
图4 举折参数模型

建立S与B和R相关的表达式后就能用参数S表示B和R,实现参数之间的关联。H1、H2、H3也可以用S来表示,以H1为例:

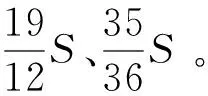
根据建立的参数模型在Grasshopper里生成对应的模型。生成举折仅需用到两边端点的点,利用移动、连线、分段等功能做出折点所在的位置,图5为生成第一折的程序,以此类推可做出第二第三折。这些举折点位十分重要,对屋面以及梁柱的生成也有定位的作用。

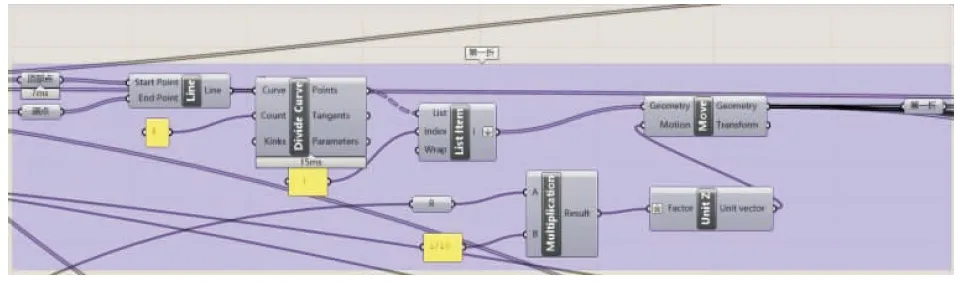
图5 第一折生成程序

利用举折点位可依次生成脊槫、上平槫、中平槫和下平槫。如图6所示,槫的作用是固定和承托屋面的椽子,将屋面荷载传递至梁柱,是重要的承接构件。槫的生成相对简单,如图8第一步骤所示,只需先做出最顶部的脊槫后,再利用偏移命令将其复制并移动到指定的位置即可。槫的截面尺寸可以椽子半径r为模数,这里取4r作为截面的长和宽。

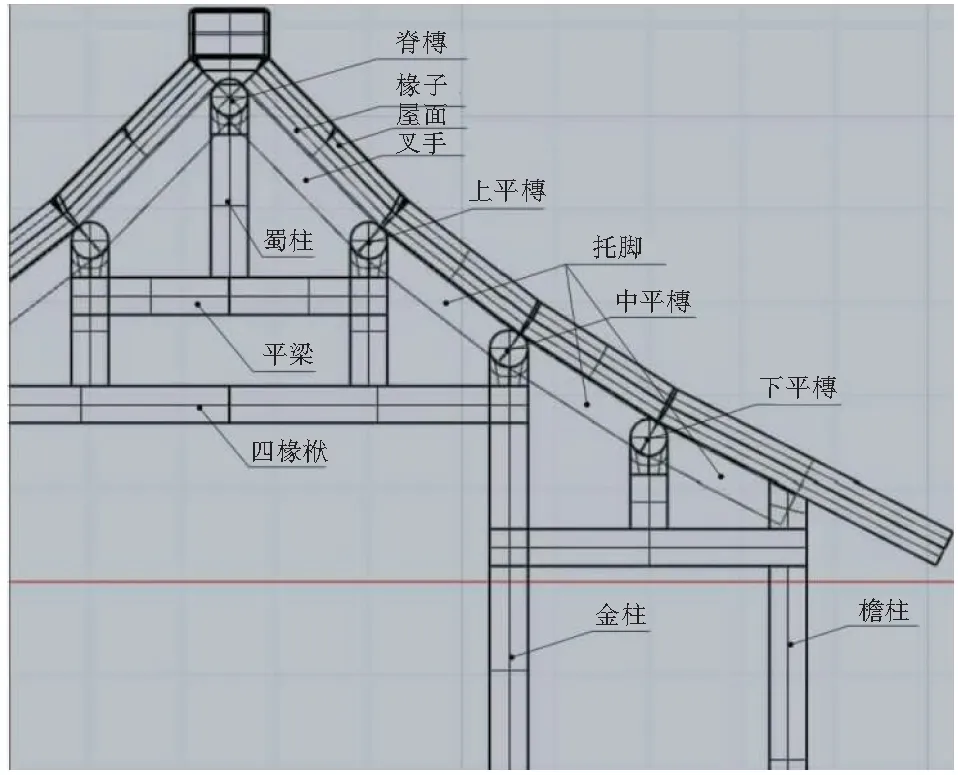
图6 构件详图

叉手和托脚也是重要构件之一,与脊槫在上端相交的斜杆称为叉手,提供斜向支撑,其他斜杆称为托脚。快速生成叉手和托脚可以使用Mesh Pipe电池,确定好初始和末尾点连成直线导入,再调整一下电池的其他参数即可生成一段叉手,再利用偏移将其移动到每个槫之间,使叉手和托脚与槫相交。

第三步生成椽子,椽子是屋面基层的最底层构件,垂直安放在檩木之上。首先引入槫顶点作为定位点,利用Cull Index电池分别去除收尾的数据,将两组数据连接成线,同时引入分段电池将连线分段并设置一个整数变量使分段数参数化,用来控制椽子的排列密度。数量控制点确定后制作椽子实体,虽然椽子的方向与叉手是基本一致的,但为了避免模型重合,需将椽子沿垂直方向进行一定的偏移,偏移量设置为一个椽子半径r,部分程序如图7所示。椽子之上是一层屋顶面,利用椽子的定位点数据和法线方向数据生成面,再沿法线方向挤出一个厚度形成屋顶面,至此建筑屋面部分建模完成,如图8所示。

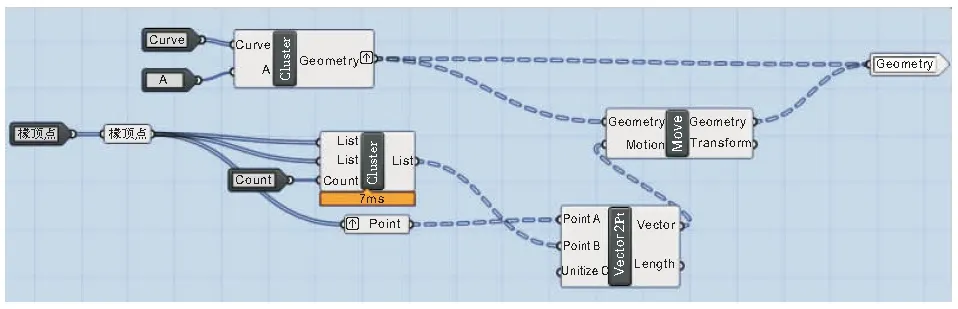
图7 椽子生成程序

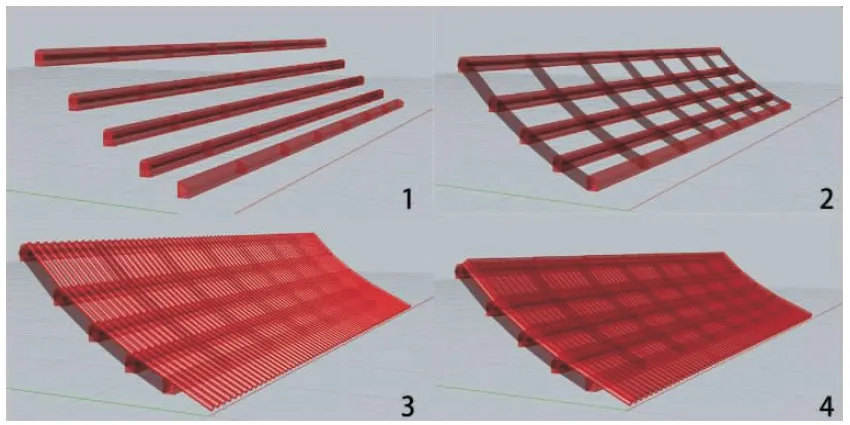
图8 屋面模型生成

最后是梁和柱的生成,其原理与生成槫的过程相似,利用移动命令对控制点进行偏移,统一生成面后挤出形成构件。生成檐柱和金柱时两柱的高度不一致,为了用一个参数控制两种柱高,将两种柱的控制点投影到一个平面上,由控制点和投影点的距离来确定柱高,通过移动平面的高度控制两种柱的高度。

屋面和梁柱完成后模型大体基本完成,对于悬山顶的特点,即屋面悬挑出山墙之外,有以下做法。利用List Item提取两端的梁柱模型进行偏移,将偏移量参数化,源数据中两端数据删除,即可对山墙面进行参数化控制。因之前做的模型只为建筑的一半,最后加上镜像命令即可完成模型的建立,如图9所示。完成的参数化模型可以对任意参数进行调整得到想要的结果,比如调整开间进深的长度、柱的截面尺寸及高度、椽的半径等,调整完成后将模型烘焙出来,导入到Blender中附上材质再渲染,如图11所示。

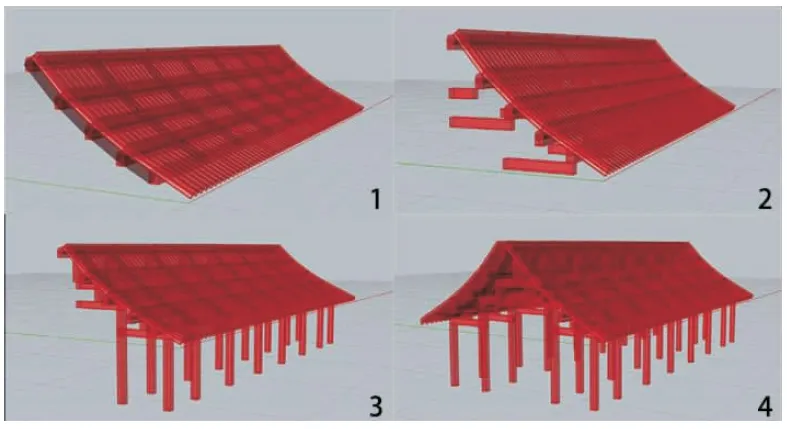
图9 梁柱模型生成

图10 模型生成程序

图11 模型渲染图

3 总结

通过研究《营造法式》,对其中的构件进行梳理,将其建造过程转换为计算机语言,实现了悬山顶建筑模型的参数化,使抽象的古建筑构件术语具象化。通过调整不同的参数即可生成相应的模型,可以减少大量的重复性工作。因笔者水平和时间有限,本文只完成了悬山顶的主要结构部分的参数化,部分复杂构件如斗拱并未实现参数化,希望在未来进一步的研究下去。