多面体外接球的一条重要性质的证明及其应用
李 勇
(息烽县第一中学,贵州 贵阳 551100)
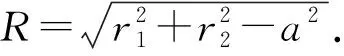
证明如图1,若侧面PAB⊥底面ABC,设△PAB的外接圆的圆心为O1,半径为r1,底面多边形的外接圆的圆心为O2,半径为r2,球心为O,球的半径为R,此侧面与底面的公共棱长为2a.取AB的中点为O3,连接OO1,OO2,OO3,AO.

图1 定理例题图
因为O1为△PAB的外接圆的圆心,
所以O1A=O1B.
又O3为AB的中点,所以O1O3⊥AB.
同理O2O3⊥AB.
又侧面PAB⊥底面ABC,
所以O1O3⊥底面ABC,O2O3⊥侧面PAB.
由球的性质,得
OO1⊥侧面PAB,OO2⊥底面ABC.
所以OO1∥O2O3,OO2∥O1O3.
所以四边形OO1O3O2为平行四边形.
由O1O3⊥底面ABC,O2O3⊂底面ABC,
所以O1O3⊥O2O3.




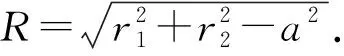
1 定理应用
例1已知A,B,C,D是球O的球面上四个不同的点,若AB=AC=DB=DC=BC=2,且平面DBC⊥平面ABC,则球O的表面积为( ).
解析设△DBC的外接圆的半径为r1,△ABC的外接圆的半径为r2,球O的半径为R.
在△DBC中,由DB=DC=BC=2,
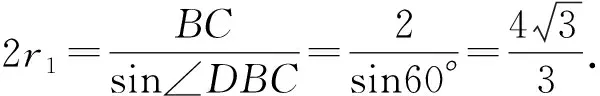

又2a=BC=2,得a=1.
所以球O的半径

例2已知等腰Rt△ABC中,AB=AC=2,D,E分别是AB,AC的中点,沿DE将△ABC折成直二面角(如图2),则四棱锥A-DECB的外接球的表面积为____.
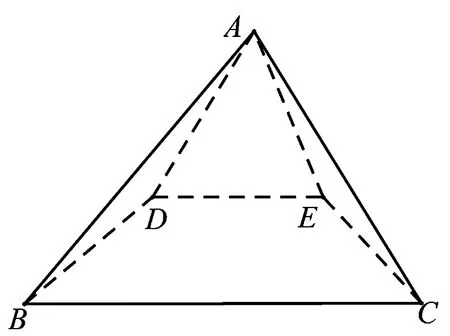
图2 例2题图
解析设△ADE的外接圆半径为r1,四边形BCED的外接圆半径为r2,四棱锥A-DECB的外接球的半径为R.
易知在△ADE中,AD=AE=1,∠DAE=90°,
得DE2=AD2+AE2=1+1=2.


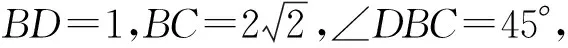
由余弦定理,得
CD2=DB2+BC2-2×DB×BC×cos∠DBC,


所以四棱锥A-DECB的外接球的表面积为4πR2=10π.

例3 三棱锥P-ABC中,PA⊥平面ABC,PA=2,△ABC是边长为1的等边三角形,则其外接球的表面积为____.
解析如图3,设△ABC的外接圆的半径为r,三棱锥P-ABC的外接球的半径为R.

图3 例3题图
因为△ABC是边长为1的等边三角形,

所以三棱锥P-ABC的外接球的半径为
例4 在三棱锥P-ABC中,PC⊥平面ABC,且PC=AB=AC=1,∠BAC=120°,则三棱锥P-ABC的外接球的表面积为____.
解析如图4,设△ABC的外接圆的半径为r,三棱锥P-ABC的外接球的半径为R.

图4 例4题图
在△ABC中,由余弦定理,得
BC2=AB2+AC2-2×AB×AC×cos∠BAC
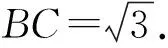


所以三棱锥P-ABC的外接球的半径为
所以三棱锥P-ABC外接球的表面积为


解析如图5,设△ABC的外接圆的半径为r,直三棱柱ABC-A1B1C1的外接球的半径为R.

图5 例5题图
在△ABC中,由余弦定理,得
BC2=AB2+AC2-2×AB×AC×cos∠BAC



故直三棱柱ABC-A1B1C1的外接球的半径为
所以三棱柱的外接球的表面积为
例6(2010年全国卷理10)设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为( ).
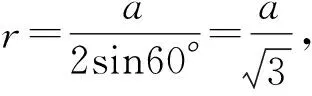
故选B.
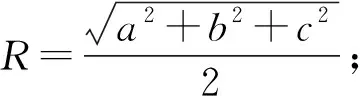
例7(2017年课标Ⅱ文15)长方体的长、宽、高分别为3,2,1,其中顶点都在球O的球面上,则球O的表面积为____.

所以球O的表面积为4πR2=14π.

A.12π B.24π C.36π D.144π

所以球的表面积为4πR2=4π×32=36π.
故选C.
2 链接练习

C.100π D.144π

A.16π B.28π C.24π D.32π




(8)已知长方体全部棱长的和为36,表面积为52,则该长方体的外接球的半径为____.
参考答案:
总之,“有一个侧面垂直于底面的棱锥与它的外接球的关系问题”是众多棱锥、棱柱的外接球问题中的一种类型.此类问题有了上述公式,就不用挖空心思地去找球的球心了,从而降低了试题的难度,使学生的解题速度得以大大提高.不过要提高解题速度,一定要记熟上述公式;还必需要熟练应用正余弦定理解三角形,用正弦定理解三角形外接圆的半径.

