基于深度学习的高三数学复习教学研究

黄文芳

［摘 要］文章着重分析高考数学“比较大小”的真题和模拟题的考查形式和命题理念。通过试题研究发现，高三数学复习教学应以培养学生的学科核心素养为出发点和归宿，并引导学生进行深度学习。

［关键词］深度学习；高三数学；复习教学；比较大小

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）11-0008-05

一、研究背景

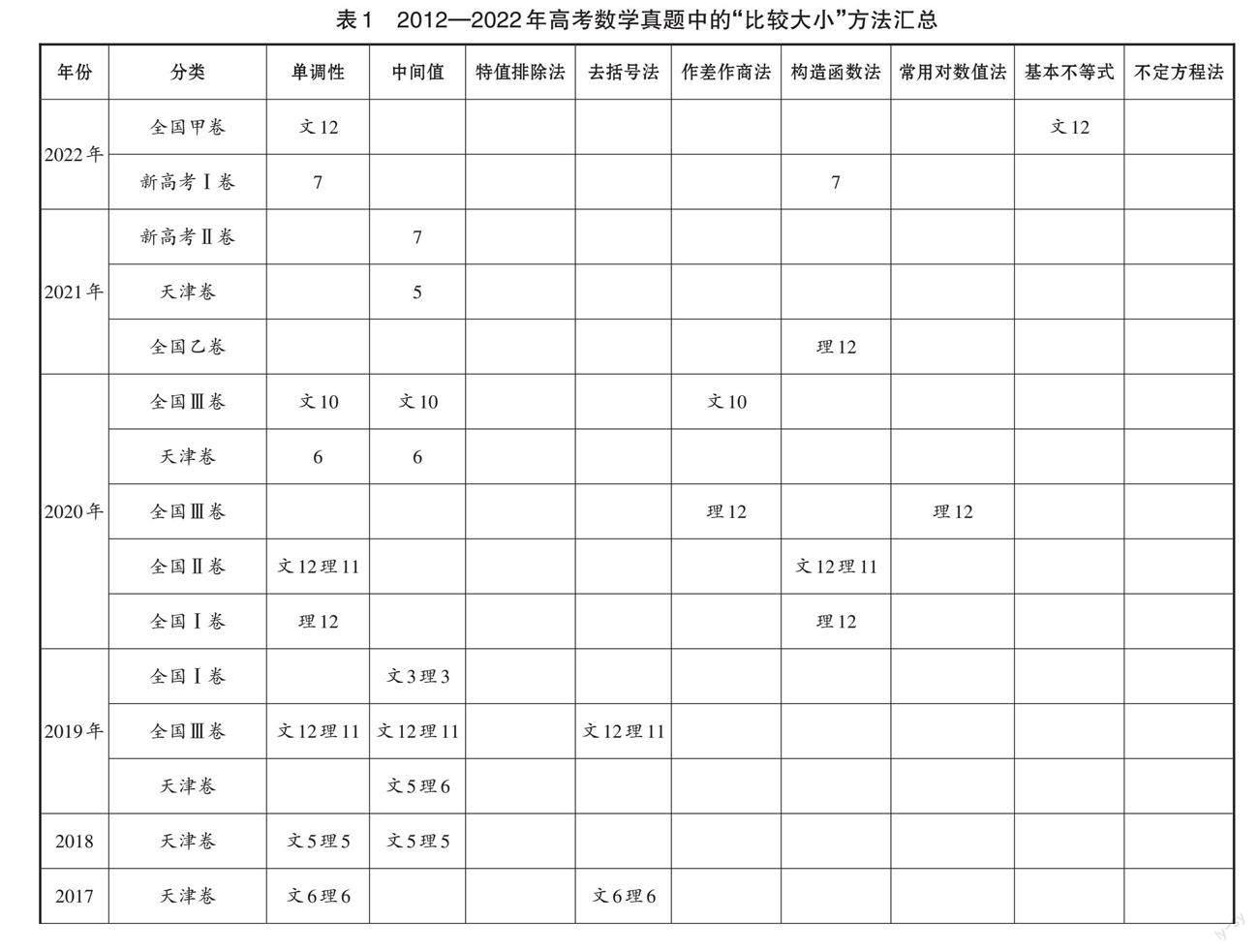
《普通高中数学课程标准（2017年版2022年修订）》中的“基本理念”强调：优化课程结构，突出主线，精选内容；把握数学本质，启发思考，改进教学。深度学习是素质教育背景下转变学习浅层化和表面化的需要，同时也是提升学生学科素养的必要路径。近几年来，高考对学生的数学学科核心素养提出了更高的要求，最直接的表现就是试题难度加大，更加注重考查学生的解决问题的能力。通过分析近十年全国高考数学“比较大小”的真题和模拟题的考查形式和命题理念发现，高三数学复习教学应以培养学生的学科核心素养为出发点和归宿，并引导学生进行深度学习。表1所示是2012—2022年高考数学真题中的“比较大小”方法汇总。

通过表1，我们发现“比较大小”问题几乎年年出现在高考选择题中，近几年有偏向压轴题的趋势。在高考模拟卷和高考卷中，此类问题的“精度”要求变得越来越高，意味着难度也越来越大。有些问题需借助泰勒展开式来处理，这无形之中增加了学生的学习负担。

笔者以近十年全国各地高考数学“比较大小”真题和各地模拟题为研究蓝本，分析了相应的高考考查形式和命题理念，并以此优化复习教学，收到了良好的效果。

二、教学案例

（一）利用指数函数、对数函数和幂函数的性质比较大小

利用指数函数、对数函数和幂函数的性质比较大小类问题是最基础的“比较大小”题型，它适用于同类型函数比较大小，即指数函数和对数函数通过讨论指数、对数的底数是大于1或者是小于1，利用单调性比较大小，而幂函数则通过幂指数的正负性判断函数值的大小。它们涉及底数、幂、真数，如果三者之一都不同，需要进行换底、换幂和换真数。

1.辨清指数函数、幂函数，提高分辨能力

［例1］设[a=0.60.6]，[b=0.61.5]，[c=1.50.6]，则[a]、[b]、[c]的大小关系是             。

分析：本题中[a]和[b]同底，[a]和[c]同幂，因此可以按照同底和同幂的性质分别比较大小，利用指数函数和幂函数的单调性比较大小。

解：先比较[a]和[b]，由于[y=0.6x]是减函数，因此[0.60.6>0.61.5]，从而[a>b]；再比较[a]和[c]，由于[y=x0.6]是增函数，因此[0.60.6<1.50.6]，从而[a

归纳：遇到同底或同幂类型的大小比较，要先分清是指数函数还是幂函数，然后再利用单调性进行大小比较。

2.灵活处理细节，提高解题能力

［例2］（1）比较[a]、[b]、[c]的大小：[a=log1312]，[b=log1323]，[c=log343]。

（2）比较[a]、[b]、[c]的大小：[a=log36]，[b=log1516]，[c=log46]。

（3）比较[a]、[b]、[c]的大小：[a=40.9]，[b=80.48]，[c=12-1.5]。

分析：指数、对数大小比較，先研究底数，若同底，则直接利用它们的单调性比较；若不同底，先用换底公式换成同底，再结合单调性比较。但对数还有一种情形，就是底数不同，但真数相同，这便再分真数大于1和真数小于1的情况得到结果。

解：（1）首先比较[a]和[b]，由于[y=log13x]是减函数，因此[log1312>log1323]，从而[a>b]；再比较[a]和[c]，由于[y=log3x]是增函数，因此借助换底公式得[log1312=log32>log343]，从而[a>c]；然后比较[b]和[c]，借助换底公式得[log1323=log332>log343]，从而[b>c]；最后得到[c

（2）[a]和[c]的真数相同，[b]的真数[16]与6有关系，通过对数的换底公式得[b=log1516=log56]，从而[a，b，c]真数均相同；根据真数6大于1，底数[3<4<5]，底数越小，函数值越大，从而有[a>c>b]。

（3）底数不同，可以换底，采用[axy=（ax）y=（ay）x]，可得[a=（2）20.9=22×0.9=21.8]，[b=（2）30.48=23×0.48=21.44]，[c=（2）-1-1.5=2（-1）×（-1.5）=21.5]，进而利用指数函数的单调性得[a>c>b]。

归纳：如果底数不同，可借助换底公式然后利用单调性比较大小。常用的换底公式为[logambn=nmlogab]，[axy=（ax）y=（ay）x]。底数不同，真数相同，真数大于1，底数越小，函数值越大；真数大于0且小于1，底数越小，函数值越小。

3.挖掘深意，提高思维能力

［例3］设[a=log23]，[b=log46]，[c=log69]，则（）。

A. [c>b>a]B. [b>c>a]

C. [a>c>b] D. [a>b>c]

分析：对数大小比较，先观察底数和真数，如果它们均不同，但是底数和真数之间存在相同的比例关系，则可以采用“换真数”的方法进行判断。

解：[32=64=96]，当真数与底数都不相同，但是真数与底数的比例相同时，可以用“换真数”的方法（用底数表示真数）：[logaxy=logax+logay]，从而[a=log22×32=log22+log232=1+log232]，[b=log44×64=log44+log464=1+log432]，[c=log66×96=log66+log696=1+log632 ]，最终比较[log232]、[log432]、[log632]三个数的大小。由于真数相同，底数不同，根据对数的图象和单调性，以及“真数相同时当底数大于1时，底数越小，函数值越大”，可得出[a>b>c]。

归纳：当真数与底数都不相同，但是真数与底数的比例相同时，可以用“换真数”的方法进行判断。

总结：在解决同类型函数“比较大小”问题时，无论是指数函数、对数函数还是幂函数，关键抓的就是底数、真数和幂，尽量通过变形化简运算使它们有一者相同，进而利用函数的单调性判断大小。

（二）与具体数字比较大小

1.借助具体数字比较

［例4］（1）已知[a=log0.53]，[b=log52]，[c=20.5]，则（）。

A. [c

C. [a

（2）已知[a=log27]，[b=log38]，[c=0.30.2]，則（）。

A. [c

C. [b

分析：同时出现了指数、对数两种类型的函数，如果底数、真数、幂不同，就要与具体数字来比较。首先借助特殊值“0”“1”来比较，但如果无法用“0”“1”时，就要借助其他数，如“2”“3”“[12]”等。

解：（1）[log0.5320=1]，[a

（2）[log27>log22=1]，[log38>log33=1]，[0.30.2<0.30=1]，此时[a]和[b]均是比1大的数，只能采取其他数。而[log27>log24=2]，[log38

归纳：当出现不同类型的函数时，首先借助特殊值“0”“1”来比较大小。如果达不到目的，需要再去找其他数，如“2”“3”“[12]”等。

2.与特殊值比较

熟记以下三个数：[ln2≈0.7]，[ln3≈1.1]，[ln5≈1.6]，当题目出现与之有关的式子时，可通过其对应的值或者对数运算法则进行大小比较。

［例5］设[a=log2e，b=ln3，c=e-23]，则（）。

A.[a

C. [c

分析：题目出现[ln2]，[ln3]，[ln5]中的一个或多个时，可以快速利用它们的特殊值进行计算比较大小。

解：[a=log2e=1ln2=10.7≈1.4]，[b=ln3≈1.1]，[c=e-23=1e23<1]，所以[a>b>c]。答案选D。

归纳：当0，1之间无法区分函数值的大小，需要更加精确的值；当出现对数时，借助几个特殊的对数值，能让答案显而易见。

3.与“[ba]”比较

［例6］设[a=log32]，[b=log53]，[c=23]，则（）。

A. [a

C. [b

分析：若题目没有出现[ln2]，[ln3]，[ln5]，可以通过换底公式用[ln2]，[ln3]，[ln5]表示，比较出[a、b、c]的大小；但是如果是随意给出的一个对数或者较复杂的对数，除了可以通过换底转化成特殊值计算，还可以用[ba]估算。由于[logab]的值与[ba]的值几乎接近，因此可用此方法比较大小。

解：[a=log32=ln2ln3≈0.64]，[b=ln3ln5≈0.69]，[c=23≈0.67]，所以[a

总结：与具体数字比较大小是选择一些满足题意的特殊值，通过与特殊值比较，从而比较出指数、对数函数式的大小的一种方式，其能将运算过程化繁为简，提高运算的速度和正确率。

（三）构造函数

利用函数单调性原理，如果一个函数是增函数且有[f（x1）

1.构造特殊函数比较大小

对形如[f（x）=lnxx]的结构，利用求导可得在[（0，e）]上递增，（e，+∞）上递减，其适用范围有以下两种情况：①[ab]与[ba]；②[logab]与[ba]。

［例7］已知[a=3ln2π]，[b=2ln3π]，[c=3lnπ2]。则下列选项正确的是（）。

A. [a>b>c]B. [c>a>b]

C. [c>b>a]D. [b>c>a]

解：[a=3ln2π=3πln2]，[b=2πln3]，[c=6lnπ]，三个数同时除以[6π]，即可以转化为[a=ln22]，[b=ln33]，[c=lnππ]，因此可以构造函数[f（x）=lnxx]，[f（x）=lnxx]在[（0，e）]上递增，（e，+∞）上递减，[b、c]在同一个单调区间内，[a]不在，务必将[a]变形为[a=ln22=2ln24=ln44]，此时[a、b、c]都在（e，+∞）上且递减，综上可得[ln44c>a]，答案选D。

归纳：对于结构类似，底数、真数或者指数反复出现的题目，可以构造函数[f（x）=lnxx]来解答，有些题目不显而易见，需要进行化简变形，注意自变量的取值范圍要在对应的单调区间上方可比较大小，如果不在，则无法比较。

2.构造一般函数比较大小

构造函数难度比较大，最关键的是先分离变量再构造函数。以变量为主，进行构造。

［例8］若[2x-2y<3-x-3-y]，则（）。

A. [ln（y-x+1）>0] B. [n（y-x+1）<0]

C. [lnx-y>0]D. [lnx-y<0]

分析：该题的算式结构很类似，且变量也相对单一，就可以用构造函数的方法比较大小。先分离变量，再构造，最后利用单调性比较大小。

解：先分离变量：[2x-3-x<2y-3-y]，再构造函数[F（x）=2x-3-x]，[F（y）=2y-3-y]，即原不等式转化已知[F（x）0]，[y-x+1>1]，所以[ln（y-x+1）>0]。答案选A。

三、结语

与指数式、对数式、幂函数式相关的比较大小的试题，集指数函数、对数函数、幂函数、导数、不等式等众多知识于一体，综合性强，解题方法灵活多样，体现了对数学抽象、逻辑推理、数学建模、数学运算以及直观想象等学科核心素养的考查。除本文介绍的方法外，还有作差作商、基本不等式等方法。在实际的解题过程中，可根据题目的条件选择恰当的方法，以使解题效果最优化。

总之，对高三数学复习课来说，课堂教学是基础，深度学习是过程，发展学科核心素养是目标，三者逻辑相关，有机统一。开展基于深度学习的高三数学复习教学，有助于培养学生的数学学科核心素养，为学生高效地复习提供保障。

［   参   考   文   献   ］

［1］  中华人民共和国教育部.普通高中数学课程标准：2017年版2020年修订［M］.北京：人民教育出版社，2020.

［2］  刘晓玫.深度学习：走向核心素养［M］.北京：教育科学出版社，2019.

［3］  白军祥.比较大小问题的题型归纳与教学启示：从一道“八省联考”试题谈起［J］.中学数学教学参考， 2022（9）：25-27.

［4］  郭学博.“幂指对”大小的比较解析［J］.中学生数学，2021（9）：7-8.

（责任编辑 黄桂坚）