高频相位激光测距系统的高精度鉴相

孟语璇， 董登峰*， 周维虎， 纪荣祎， 朱志忠

（1.中国科学院 微电子研究所，北京 100029；2.中国科学院大学，北京 101408）

1 引 言

相位式激光测距技术具有响应快、量程大、抗干扰能力强、精度高等优点，被广泛应用于航空、航天、船舶和机器人等大型装备制造领域［1-6］。高端装备制造对于测距精度的要求已从亚毫米提升至数十微米量级，传统的相位式激光测距方法和系统性能迫切需要提升。由激光测距原理可知，信号调制频率和鉴相精度是影响相位激光测距精度的主要因素［7-8］。

滕晓［9］采用调制频率为40 MHz的激光进行测距，系统鉴相精度在0.1°量级，测距精度在毫米量级，但是较低的激光调制频率限制了测距精度。王心遥等［10］使用80 MHz的调制信号进行测距仿真，鉴相精度为0.1°左右，测距精度可达0.68 mm。姜成昊［11］采用光频调制技术产生频率100 MHz的信号进行测距，系统的鉴相精度可达0.1°，测距精度优于0.5 mm。由上述研究可知，在鉴相精度大体相当的情况下，随着调制频率的升高，测距精度同步升高。通常采样频率数倍于激光调制频率，随着信号调制频率的升高，对采样频率的要求也会越来越高，但是高速采样会受到（Analog-to-Digital Converters， ADC）器件采样频率的限制。为解决上述问题，人们将欠采样方法用于相位测距［12］。欠采样［13］方法过去曾被用于雷达信号测频。若用欠采样方法进行相位测距，则可在较高的调制频率下实现较低的采样频率，既提高调制频率，又降低对ADC采样频率的要求，有利于提高相位测距精度。

在确保高调制频率的条件下，采用先进的鉴相策略，进一步提高鉴相精度也是提高绝对测距精度的重要环节。孙懋珩，赵雯等［14］仿真对比了基于欠采样的数字同步解调法和频域谱分析法（Fast Fourier Transform，FFT），发现频域谱分析法的鉴相精度更高，仿真鉴相误差为0.1°。王选钢和缑宁祎等［15］将希尔伯特变换用于FFT法，减小了鉴相偏差，在信噪比为40 dB、调制频率为100 MHz时，仿真鉴相精度可达0.1°。王兆华和侯正信［16］改进了FFT方法，提出了apFFT法，并认为apFFT可以使始端和终端保持连续，避免采样信号起止点和终止点的相位不连续，能够有效抑制频谱泄漏［17］。但上述方法大多基于仿真研究，没有开展实际测距系统的实验验证。

目前，调制频率最高大约为100 MHz，测距精度在亚毫米量级，无法满足高端装备制造的高精度测距需求。本文提出欠采样与apFFT融合的方法，将调制频率提高至200 MHz，采用apFFT进行鉴相，充分利用两者的综合优势，大幅度提高鉴相精度，从而提高激光测距精度。

2 相位测距原理

相位式激光测距是通过测量激光从起点到被测目标往返的相位差来间接测量激光飞行时间的测距技术。相位激光测距信号的往返过程见图1。图中：点O为激光发射点，点O'为测距信号接收点，两者为同一个点，A点为被测目标点，x是待测距离，φ是信号从发射到接收信号变化的相位。

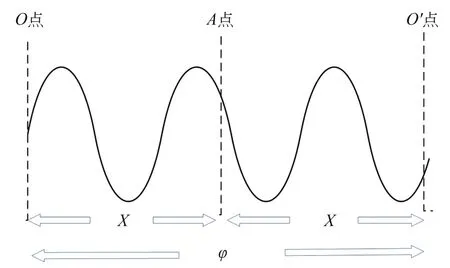
图1 相位式激光测距信号往返Fig.1 Round-trip of phased laser ranging signals

激光由发射器从点O发出到达目标物点A，经点A反射回点O'，由探测器接收。此过程中，假设激光的飞行时间为t，飞行速度为c，则从起点到终点的距离为：

式中飞行时间t可由相位φ求出，即：

式中：φ是激光往返的相位变化，f是信号调制频率。由式（1）和式（2）可得：

由式（3）可知，所测距离由φ和f决定，已知调制频率f，只需测出相位差φ即可求出待测距离x。相位激光测距系统原理如图2所示。

图2 相位式激光测距系统原理Fig.2 Schematic diagram of phase laser ranging system

在激光测距系统中，为了降低噪声的影响，激光器调制后的信号通过分光镜，一部分作为参考信号，直接通过光路，由APD接收；另一部分作为测量信号，由目标物反射后，再由APD接收；将参考信号和测量信号送入鉴相系统，通过对参考信号和测量信号鉴相分别求出相位φ1和φ2，两者做差即可求出变化的相差φ，并通过式（3）计算距离x。显然，相位测距精度与φ的鉴相精度相关，鉴相精度越高，测距精度就越高。

在系统工程实现时，想要获得好的鉴相精度，需要考虑各方面的影响，比如调制频率、采样器件和鉴相方法等，本文综合考虑这些因素，提出采用“欠采样+apFFT”的方法实现鉴相系统。与正常采样法相比，欠采样法在低的采样频率下能够获得更高的信号调制频率；全相位频谱分析法抗干扰能力强、鉴相精度高；将两种方法结合，实现测距系统的鉴相并进行测距系统验证。

3 仿真分析

3.1 欠采样对鉴相精度的影响

Nyquist定理要求对信号采样时要满足式（4），理论上才能恢复出原始波形。

式中：fs是采样频率，fm是信号频率。

在实际电路中，由于各种噪声的影响，采样频率要远高于式（4）中的采样频率，才能比较好地恢复原始信号［18］。但过高的采样频率对硬件的要求很高且伴随着高频串扰，在具体实现时难度很大。传统方法使用混频电路［19］，降低携带相位信息的高频信号频率，达到降低采样频率的效果，但该方法电路复杂，且易引入干扰，降低鉴相精度。为解决上述问题，同时考虑到相位测距无须恢复原始信号，只需提取对应的相位信息的特点，本文提出欠采样的方式，在降低采样频率的同时简化硬件复杂度，减少干扰。

值得一提的是，欠采样的方法会使信号的频谱发生搬移。假设要提取频率为fm的信号携带的相位信息，则欠采样后变为提取f'频率处的信息，如下：

式中：fm是信号频率，fs是采样频率，［·］是向下取整，f'是欠采样后携带原频相位信息的谱线频率。

为了分析欠采样方法的可行性，首先采用仿真法研究欠采样对鉴相精度的影响，仿真生成两路频率为201 MHz、相位不同的正弦信号，均加入40 dB的高斯白噪声，两路信号的相位差分别设为10°，30°，170°，180°，200°，330°，依次用不同的采样率对信号采样，得到不同采样率下的鉴相结果，如图3所示，可以比较欠采样和正常采样的鉴相精度。

图3 信号频率为201M时不同相位差下欠采样与正常采样的鉴相误差Fig.3 Undersampling and normal sampling phase discrimination error under different phase differences with signal frequency of 201M

图3为调制频率fm固定，采样频率变化的鉴相误差，横坐标是采样频率fs，纵坐标是调制信号fm为201 MHz时仿真计算的相位差与设定相位差的偏差，参考线fs=2fm的左边代表欠采样，右边代表正常采样。从图中可以看出，当选取采样频率是调制频率的倍数402 MHz时，在附近区域出现较大的鉴相误差；除此之外，参考线左边和参考线右边整体鉴相误差相近，说明欠采样和正常采样在此区域内的鉴相误差相近，如果选取欠采样频率得当，欠采样不会影响鉴相误差。因此，合理选用欠采样频率不会导致鉴相精度变低，欠采样方法用于相位测距具有可行性。后续测距系统的采样频率选用100 MHz。

3.2 鉴相方法精度

相位测距广泛采用数字鉴相，主要方法有正交法、相关法，及利用频域鉴相等方法［20］。正交法抗高斯白噪声能力较弱，相关法对信号采样要求严格。相较上两种方法，频域鉴相法有较高的鉴相精度，可与欠采样方法结合实现高精度鉴相。频域鉴相主要有FFT和apFFT两种方法。

相较于FFT，apFFT增加了预处理过程，具体步骤如下：

（1）两个长度为N汉宁窗卷积，得到长度为2N-1的卷积窗；

（2）对长度为2N-1的卷积窗进行归一化；

（3）用归一化的卷积窗对长度为1∶2N-1的时间序列信号加权；

（4）将第1项与N+1项，第2项与N+2项，…，第N-1项与第2N-1项相加，得到N点时间序列；

（5）对预处理后得到的N点序列再进行FFT。

FFT变换公式如下：

其中：x(n)为长度从0，1，2，…，N-1的N个时域序列，X(k)为长度从0，1，2，…，N-1的N个频域序列。FFT将时域的N个点变换为频域的N个点，频域各点分别携带不同频的实部、虚部信息。

序列点与频率的对应关系如下：

其中：k'代表频域的序列点数，N是FFT的计算点数，fs是采样频率。正常采样时，f'是信号的频率；欠采样时，f'是据式（5）得出的频率。

综合式（4）～式（6）可得对应频率的实部、虚部信息，如下：

所求信号的相位差为：

为了对比分析FFT和apFFT两种频域鉴相方法的特性，采用仿真法生成频率为201 MHz的正弦信号，采样频率为100 MHz，初始相位在0°～350°变化，并设置多组计算点数不同的对照组，计算点数分别设为2 000，4 000，6 000，8 000。FFT法结果见图4（a），apFFT法结果见图4（b）。

图4 FFT和apFFT法在不同相差和计算点数下的鉴相误差Fig.4 Phase discrimination error of FFT and apFFT methods under different phase differences and calculation points

如图4（a）所示，FFT法在计算点数为2 000，4 000时鉴相精度在±0.000 12°左右，点数为6 000时鉴相精度优于±0.000 08°，计算点数为8 000时鉴相精度在±0.000 02°左右，高于其他对照组。如图4（b）所示，当apFFT法计算点数为8 000时鉴相误差最低，精度在±0.000 002°左右，远高于其他计算点数的对照组。对比图4（a）和4（b），FFT法和apFFT法均在8 000的计算点数下鉴相精度最高，且apFFT法的鉴相精度比前者高一个数量级。

实际测距过程中，由于仪器电磁干扰和外部环境干扰，测距信号有较大噪声，影响鉴相精度，本文进一步仿真比较两种频域鉴相方法的抗噪性能。测距时，参考信号直接从内光路得到，受到的噪声干扰较小。相比而言，测距信号更易受到外界噪声的干扰。MATLAB仿真时，两路信号均加入高斯白噪声，参考信号的信噪比设为45 dB，测距仿真信号的信噪比从5 dB增加到50 dB，变化步长设为5 dB，在每个信噪比下进行多次鉴相，计算鉴相均值，并求出与预设相差的绝对误差，结果如图5所示。

图5 不同信噪比两种鉴相方法的鉴相误差对比Fig.5 Comparison of phase detection error of two phase detection methods with different signal-to-noise ratios

如图5所示，随着横轴信噪比的增大，FFT法和apFFT法的鉴相误差逐渐减小，在15 dB之后减小趋势变缓，误差趋于稳定，FFT法的误差稳定在0.006～0.009°内，apFFT法的误差稳定在0.002°以下。在相同的信噪比下，apFFT法的鉴相误差始终小于FFT法。仿真结果表明，在信号频率为201 MHz，采样频率为100 MHz，相同信噪比时，apFFT法优于FFT法。

另一方面，考虑到相位激光测距系统中激光信号频率源不稳定可能导致参考和测量信号采样存在偏移，影响鉴相精度。为此仿真分析存在频率偏移时两种频域鉴相方法的鉴相精度。设置参考信号频率为201 MHz，信噪比为45 dB；测量信号频率为201 MHz±4 Hz，信噪比为35 dB，每个频率下进行1 000次仿真鉴相，结果如图6所示。

图6 不同频率偏移时两种鉴相方法的鉴相误差Fig.6 Phase detection error of two phase detection methods at different frequency offsets

图6中，当测量信号频偏为0时，FFT法的鉴相误差最小，随着频率偏移的增大，FFT法的鉴相误差逐渐增大。apFFT法在频率偏移的过程中，误差变化很小。仿真结果表明，当测量信号存在频率偏移时，相较FFT法，apFFT法鉴相具有更好的抗频率偏移能力，鉴相精度优于前者。

最后，考虑到实际ADC的采样信号存在多种噪声，故直接利用ADC采样到的信号进行频域鉴相，鉴相误差如图7所示。

图7 实际采样信号下FFT和apFFT的鉴相误差Fig.7 Phase discrimination errors of FFT and apFFT under actual sampling signals

图7（a）比较了在不同预设相位差下FFT法多次鉴相的误差，最大鉴相误差大约在±0.06°左右；图7（b）比较了在不同预设相位差下apFFT法多次鉴相的误差，最大鉴相误差大约在±0.04°左右；综合比较图7（a）和7（b）可得，apFFT鉴相精度整体要优于FFT。

实际上，当采样为整周期时，频谱泄漏最小，频域分析鉴相精度最高。FFT法要尽可能调整采样频率和采样点数以达到整周期采样，但实际结果一般会存在极小的差距，影响鉴相精度。而apFFT法对采样序列进行预处理后，对于任何采样频率和采样点数，均可达到采样整周期的效果，因此相较FFT法，apFFT法具有“相位不变性”［21］，故精度高于FFT法。

综合考虑以上仿真结果，系统采用apFFT的鉴相方法。

4 实 验

为了实现大范围高精度的激光相位测距，在仿真分析基础上设计鉴相电路系统，其主要参数如下：信号频率为201 M，采样频率为100 MHz，计算点数为8 000，系统主时钟为100 MHz。测距系统的主控电路使用XILINX的XC7K325T系列，采样芯片使用AD9250。鉴相电路流程如图8所示。

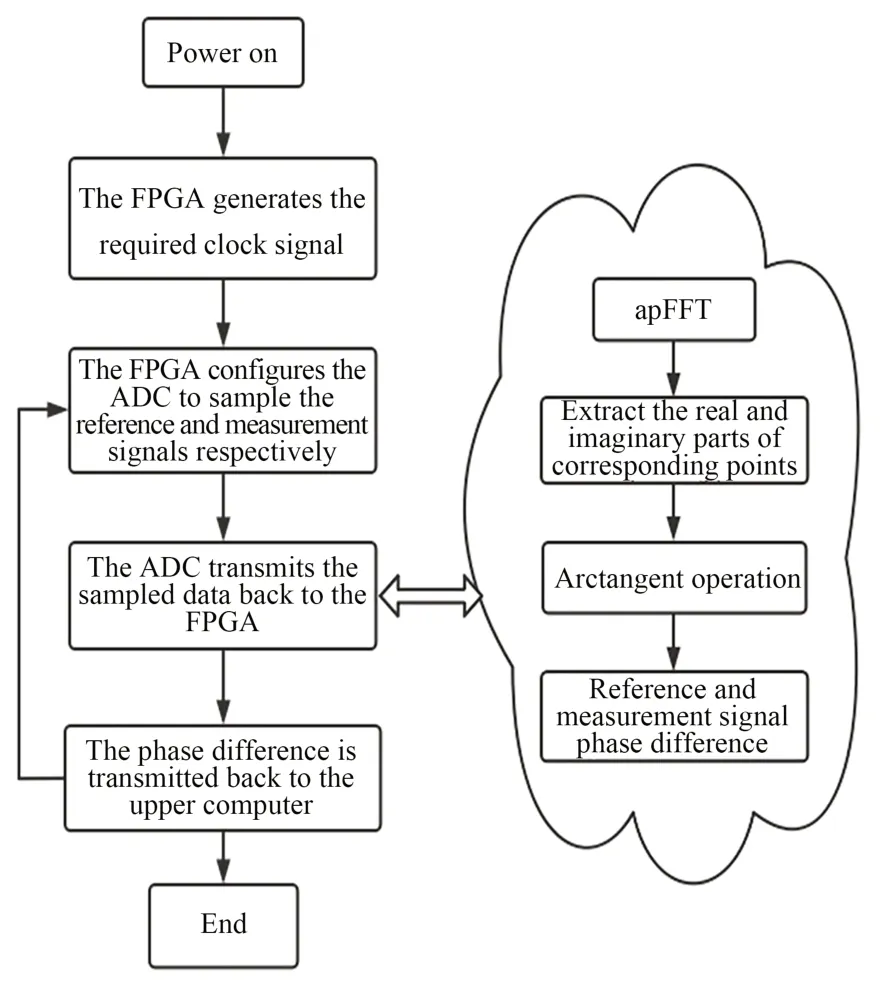
图8 相位式测距鉴相系统框图Fig.8 Block diagram of phased laser ranging system

如图8所示，相位测距鉴相系统的工作流程如下：

（1）系统上电；

（2）FPGA生成一系列时钟信号；

（3）FPGA作为主控电路［22］，通过SPI协议配置AD9250工作模式，控制它对参考和测距信号进行采样；

（4）AD9250将采样数据通过JESD204B协议传给FPGA，由FPGA内部进行数据处理，包括apFFT处理、提取相应序列谱线、反正切变换、求相位差等操作；

（5）FPGA等待上位机指令，得到指令后将相位差数据通过串口传回上位机显示。若得到多次鉴相指令，返回第三步，进行多次测量。

为测试测距电路的性能，按图2相位测距原理图搭建测距系统，实物如图9所示。

图9 高频相位测距光路系统和鉴相系统Fig.9 Optical and phase detection system of high-frequency phase ranging circuit

图9（a）为测距电路的光路系统，图9（b）为相位测距电路的鉴相系统。测距电路使用12 V电压供电，使用安捷伦81150A信号发生器产生两路相位不同的正弦波，相位差分别设置为10°，160°，230°，280°及350°，进行多次鉴相，将相位结果传输到上位机显示。随机选取3次鉴相结果，如表1所示。多次测量的相位误差如图10所示。

表1 相位测量结果Tab.1 Result of phase measurement（°）

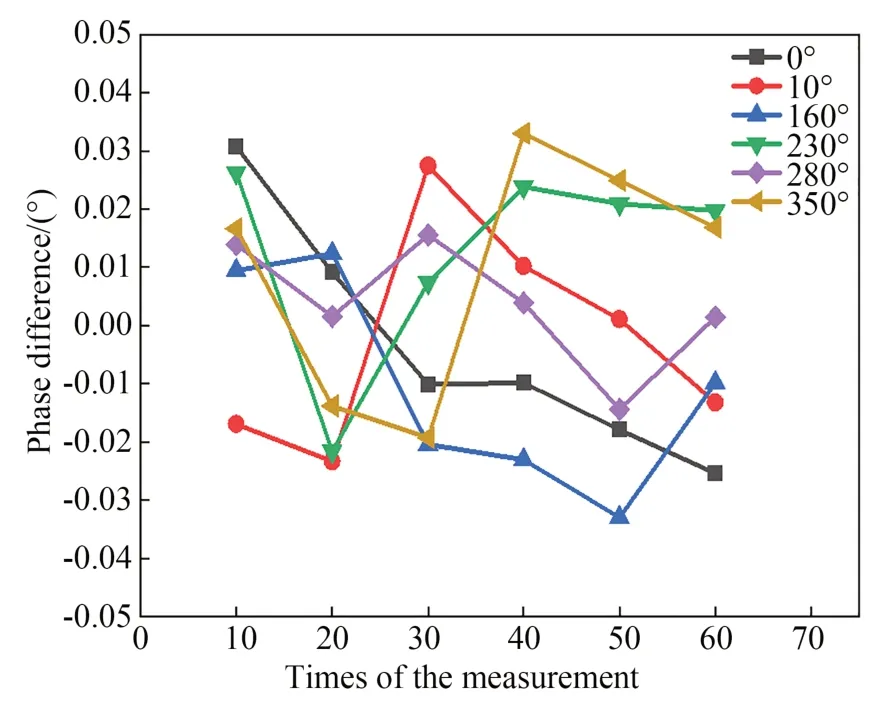
图10 测量的相位差与实际相位差的误差Fig.10 Error between measured phase difference and actual phase difference

表1是从多次鉴相结果中随机选取3次的鉴相数据，其中第1列是标准相位差，后3列为鉴相数据。观察表中每行可以看出，实际鉴相结果与标准相位差相近，鉴相误差均小于0.04°。

如图10所示，在不同预设相差下，鉴相误差大约在±0.04°以内，对应的测距精度为±0.08 mm。

图11表征了鉴相系统的重复性。从图中可以看出，不同相差下，标准差在0.005～0.02°之间变化，鉴相系统的重复性较好。

图11 不同相位差下多次测量的标准差Fig.11 Measurement standard deviation of different phase differences

5 结 论

本文从原理和系统实现方面分析了提高相位测距精度的方法，即提高调制频率和鉴相精度。针对这两种方法仿真对比了欠采样和正常采样的鉴相误差，分析了欠采样方法的可行性；在此基础上仿真比较了FFT和apFFT在不同相差和采样点数影响下的鉴相误差，以及两者对高斯白噪声和频率偏移的抗干扰能力，对比得出apFFT法的鉴相和抗干扰能力更强。最后，根据仿真研究结果构建了基于FPGA的欠采样全相位激光测距系统，当待测信号为201 MHz，计算点数为8 000点时，系统的鉴相精度优于±0.04°，测距精度为±0.08 mm左右，系统方差小于0.01，较为稳定。这表明本文提出的“欠采样+apFFT”方法在高精度激光测量领域具有重要的应用价值。